참고자료
https://www.youtube.com/watch?v=3gzI4Z2OFgY&list=PL-wATfeyAMNqIee7cH3q1bh4QJFAaeNv0&index=16
이 강의를 내가 보고 내용을 살짝 첨가해서 씀 글이 이해안되면 위 유트브를 참고하면 좋다.
STFT
전 시리즈에서 DFT와 spectral leakage를 보며 전처리에서 fourier transfrom이 어떻게 이용되는지 알아봤다.
DFT를 이용한 데이터는 우리가 딥러닝에 이용할 수 없다.
우리가 음악을 들을 때 가장 중요한 게 바로 시간의 흐름이다. 음과 리듬은 모두 시간이 진행되며 변화하는 데 그걸 즐기는 게 바로 음악이다.
그래서 음악 딥러닝에서도 당연히 시간의 흐름이 중요하다.
근데 DFT는 시간을 구하는 게 아닌 전체 입력 신호의 주파수 성분을 분석한다.
그래서 우리가 음악 딥러닝에는 사용할 수 없다. 왜나면 시간이 포함된 데이터를 주파수 데이터로 바꿔 시간 데이터가 없어지니
이걸 어떻게 해결할까? 간단하게 생각해보자.
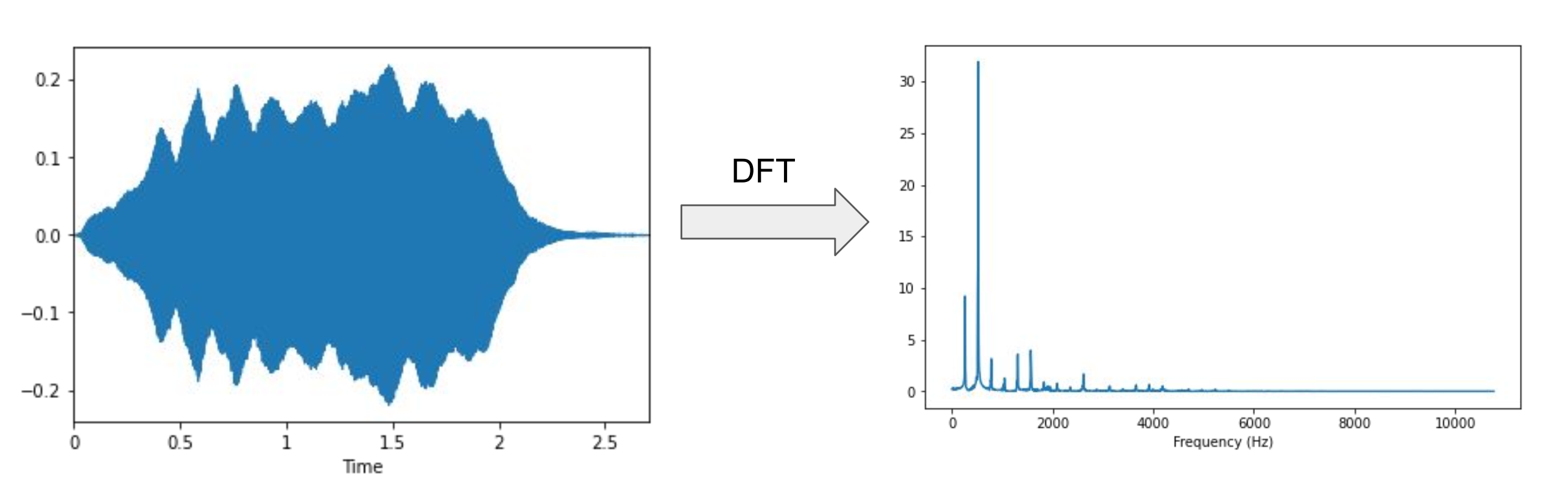
음악 딥러닝에 필요한 데이터의 특성은 다음과 같다.
- 주파수 성분
- 시간
- 음압(크기)
DFT는 이중 시간을 제외한 주파수 성분과 신호의 크기만 알 수 있다.
시간의 데이터를 얻을려면? 입력신호를 잘게 쪼개면 어떨까?
DFT의 문제점이 전체 긴 시간의 모든 주파수 성분을 보여주는 건데 전체 시간을 분석하는 게 아닌 잘게 쪼갠 작은 입력신호를 DFT한다면? 또한 잘게 쪼갤때 일정한 시간 간격으로 입력신호를 나누고 쪼개서 각각의 데이터에 순서를 부여한다면?
DFT의 데이터 벡터가 (주파수, 음압) 이라면
잘게 쪼갠 데이터의 벡터는 (주파수, 음압, 전체 데이터 중 해당 데이터 순서) 이렇게 표현되면 우리는 시간 간격을 알 수 있으니
시간 간격 * 해당 데이터 = 해당 데이터 시간 구간
이렇게 DFT에 시간 데이터를 추가해서 아는 것이 STFT(short-time-fourier-transform)이다.
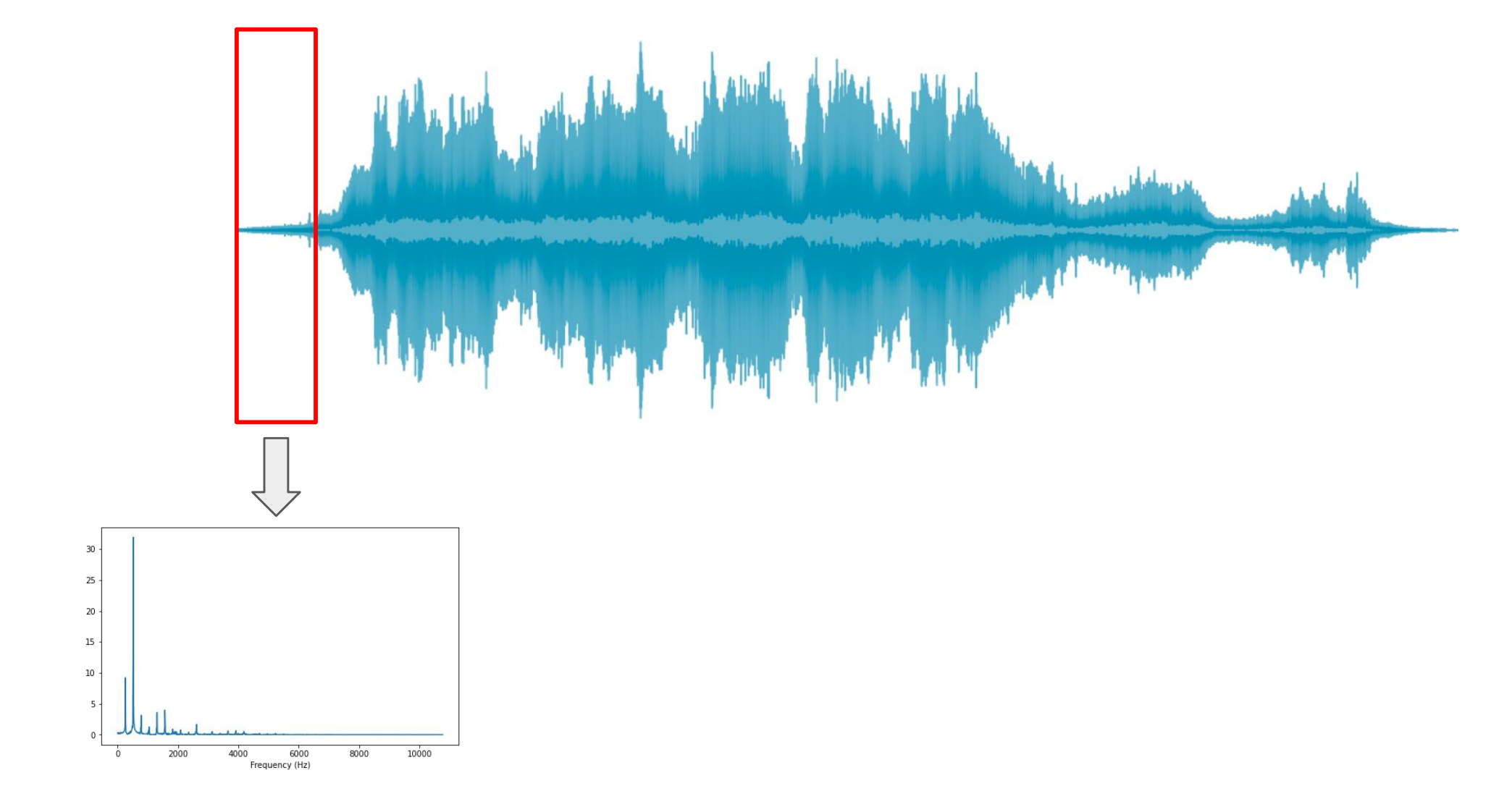
위 그림과 같은 입력신호 중 짧은 시간 간격만 따로 DFT를 하자.
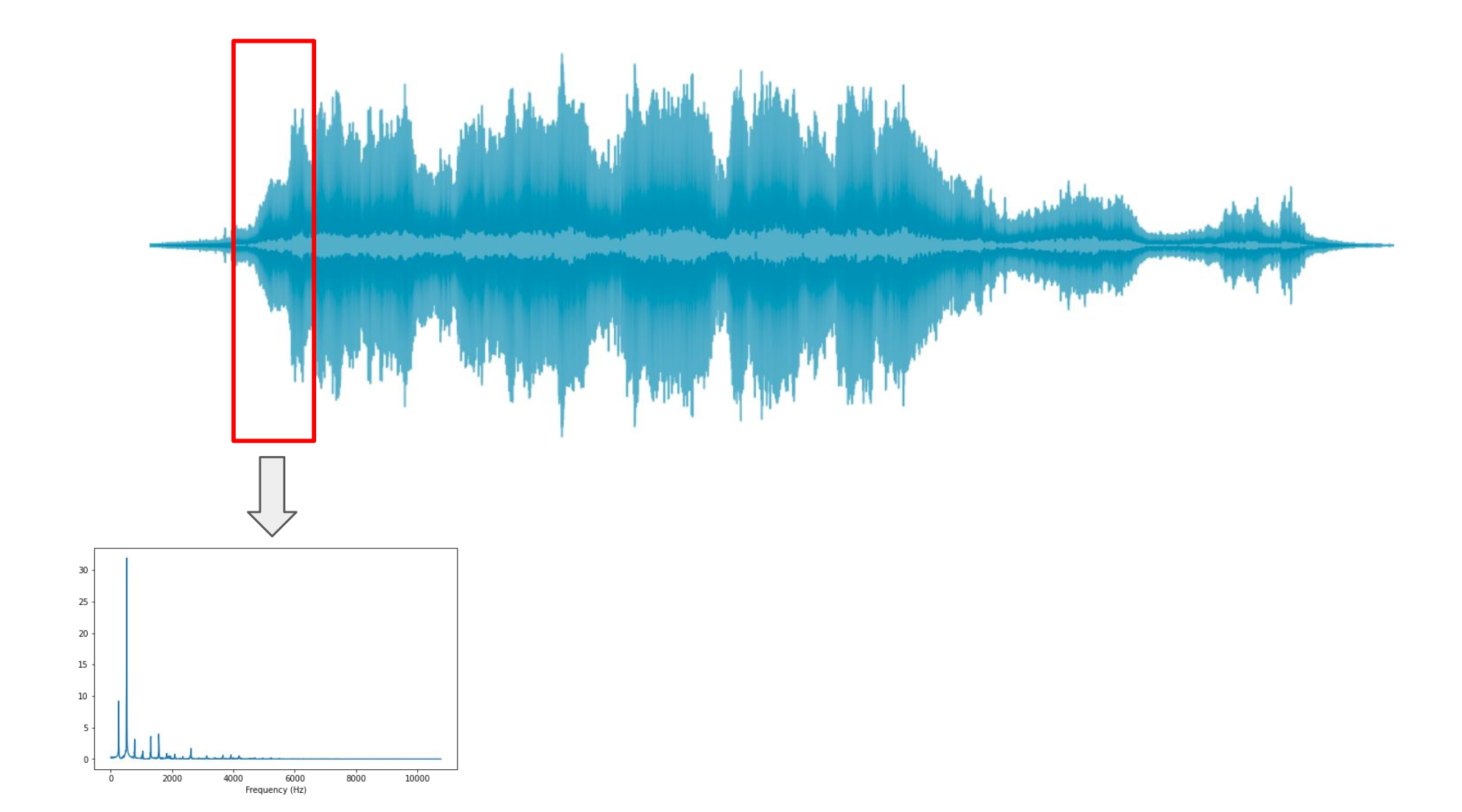
다음으로 일정하게 구간을 움직여 DFT를 해주자.
Overlapping framesize
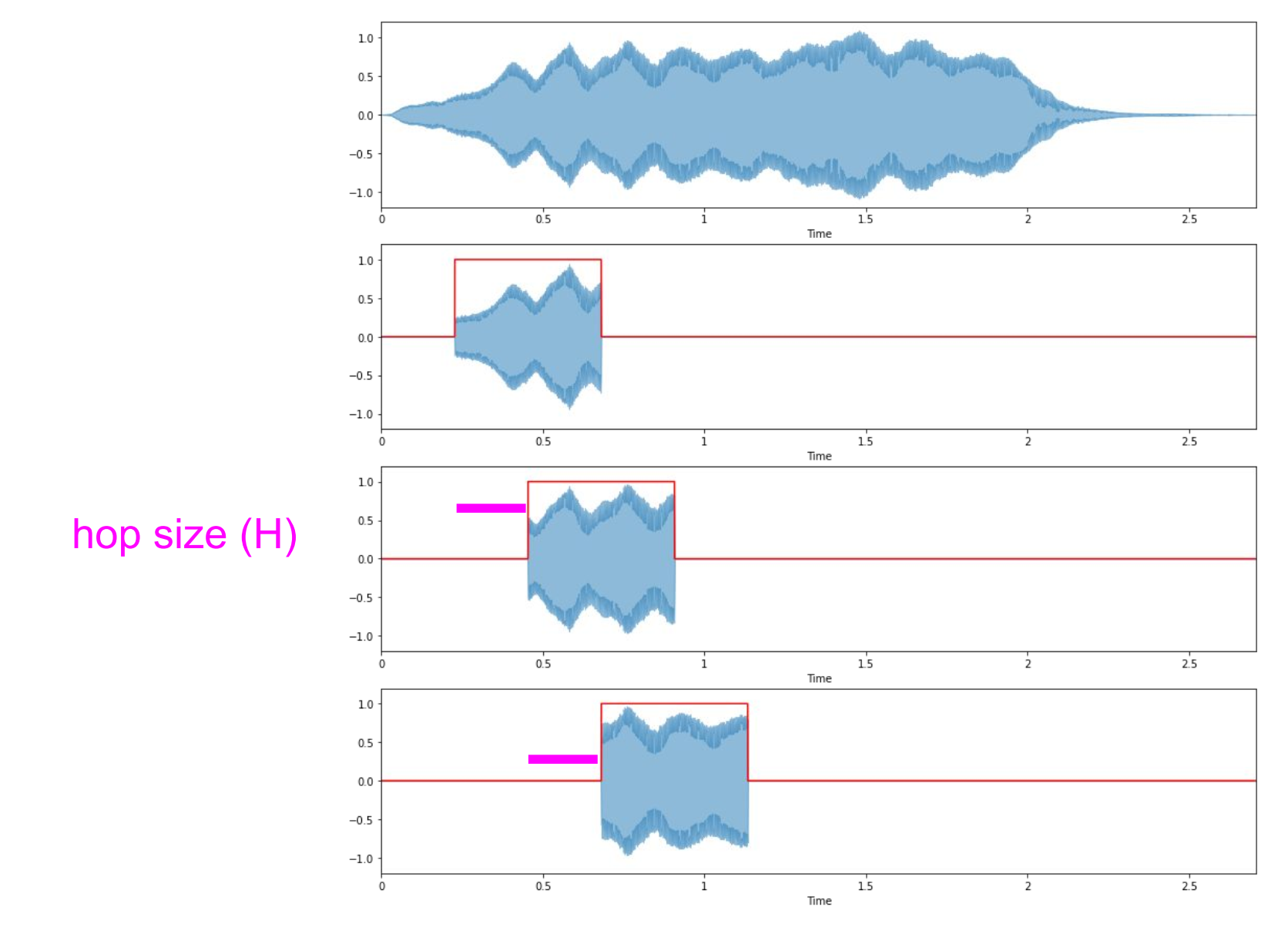
우리가 STFT를 적용할 때 각각의 프레임들의 영역을 중복으로 겹쳐서 진행한다. 이러면
-
신호의 중요한 정보 누락 가능성을 줄인다. -> 겹치지 않는다면 경계의 성분이 누락될 수 있다.
-
스펙트럼이 연속적으로 보임 -> 겹치지 않는다면 스펙트럼이 경계값에서 갑자기 불연속적으로 보인다.
-
창 함수의 효과를 더해줌
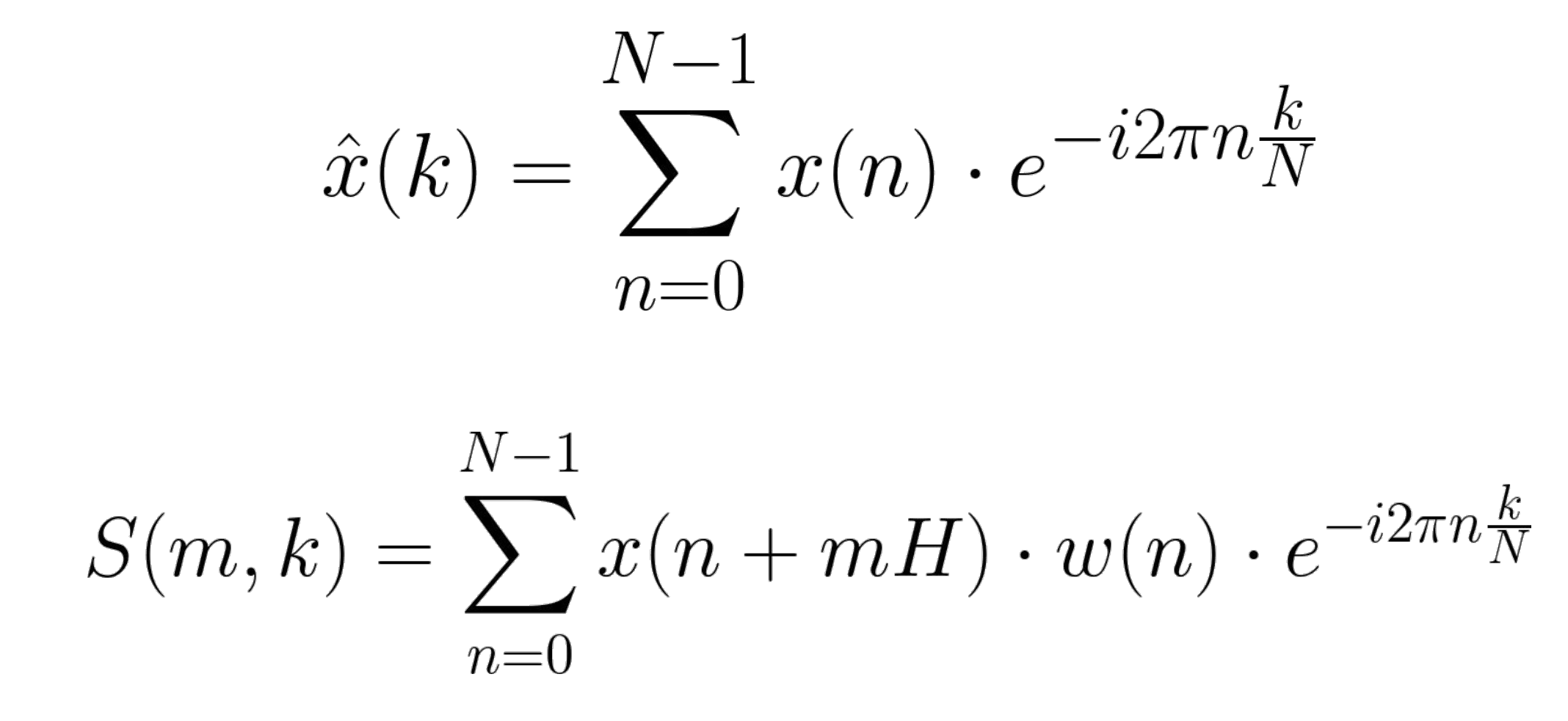
위가 DFT이고 아래가 STFT이다. H가 hoplength로 다음 프레임 영역을 정하는 기준이다. 보통 H를 framesize보다 적게하면 프레임들의 영역이 겹쳐지게 된다.
w는 윈도우 함수로 leakage를 줄여주고 신호를 연속적으로 만들어준다. 이건 나중에 다루겠다.
parameter
-
frame size는 보통 512, 1024, 2048, 4096, 8192
-
hop length는 256, 512, 1024, 2048, 4096로 보통 프레임 사이즈의 크기의 절반, 1/4, 1/8인데 절반을 보통 선택한다.
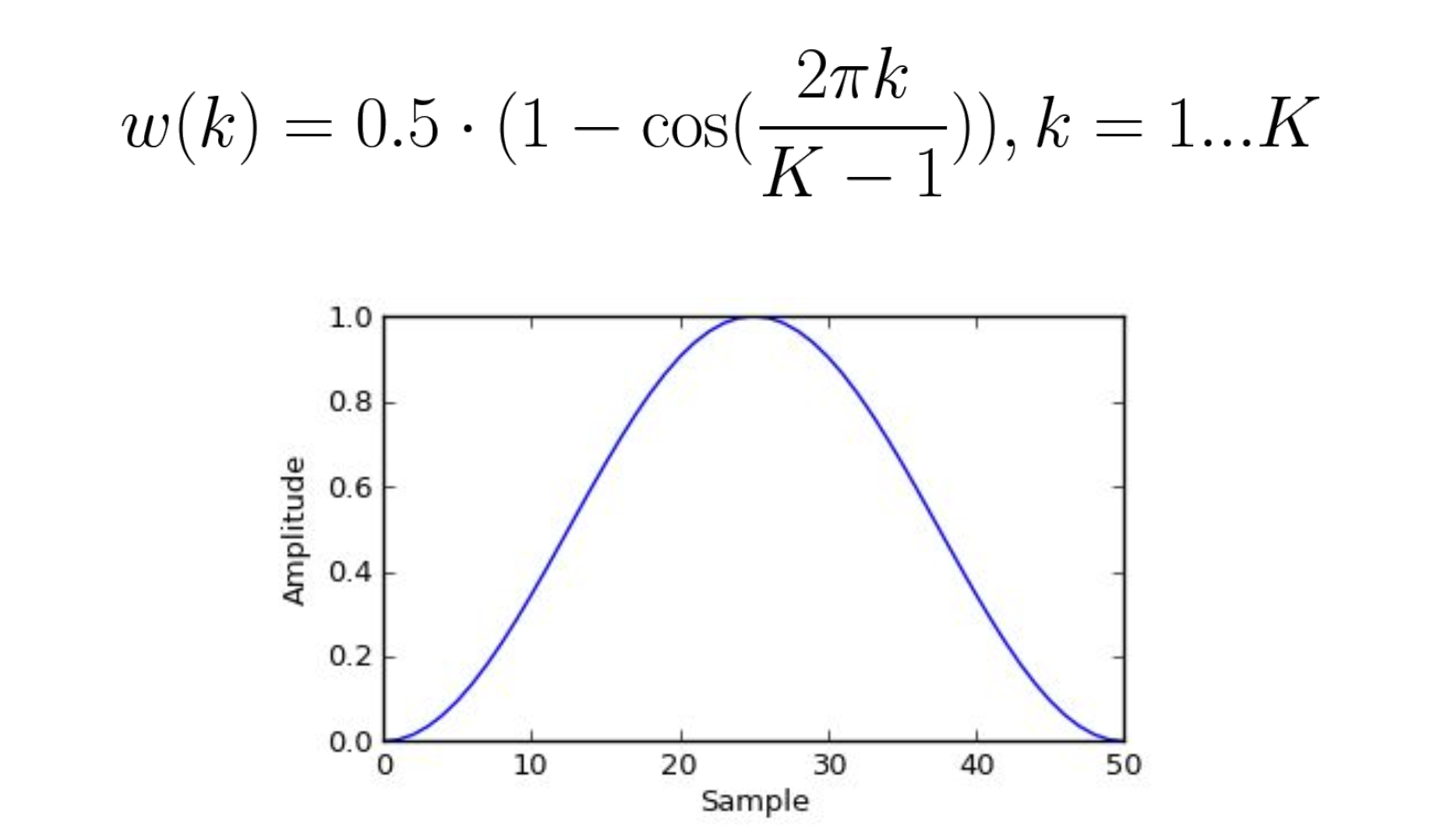
보통 윈도우 함수는 hann window funtion이라고 쓰는데 이것도 나중에 다룸
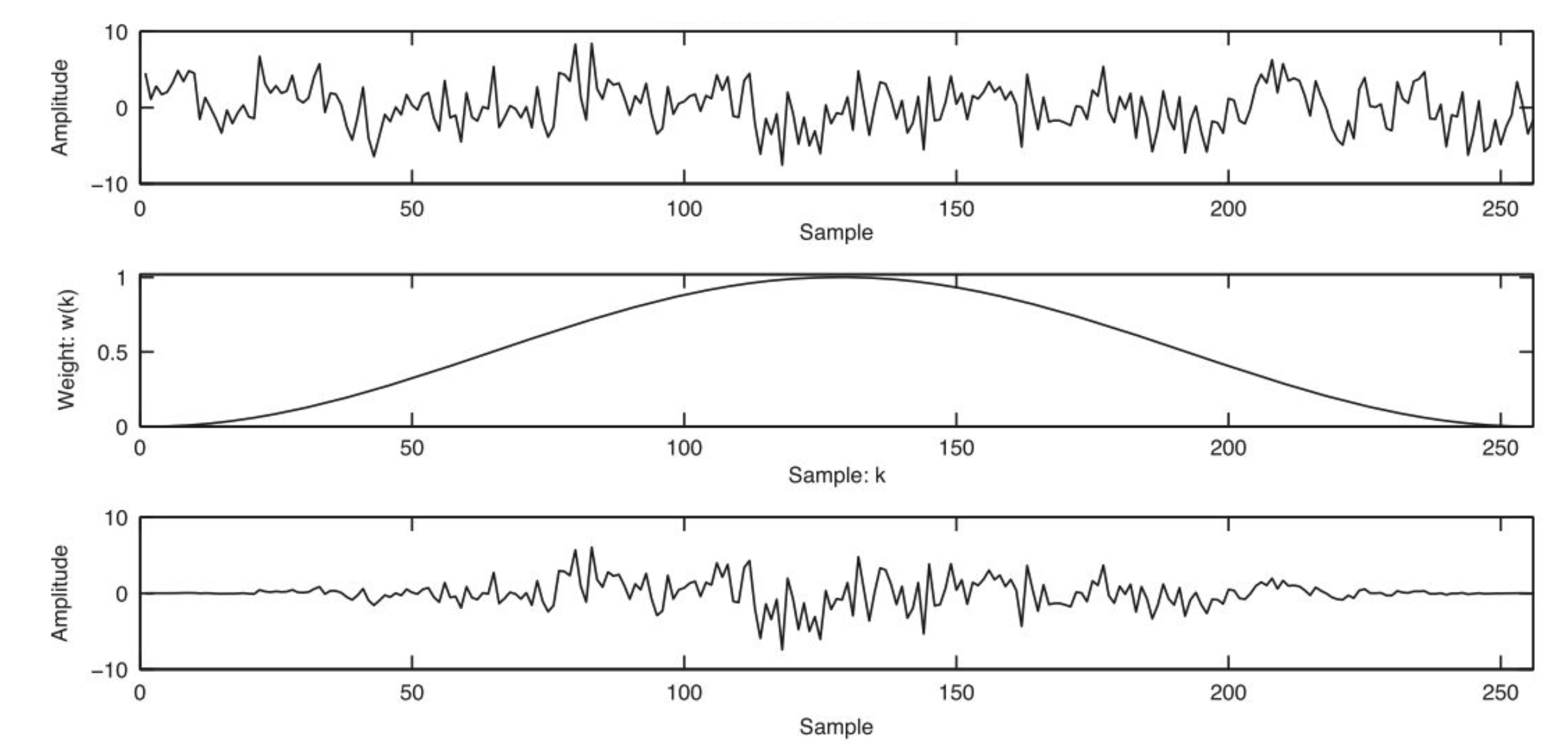
간단하게 윈도우 함수는 데이터의 처음과 끝 부분을 0으로 부드럽게 없애준다. 이러면
- hop length로 겹치는 효과가 조금 완화됨.
- 처음과 끝을 미분가능하게 부드럽게 0으로 만들어서 각 데이터를 연결했을때 연속적이됨.
푸리에 변환의 수학적 조건에 대충 연속적이고 미분 가능하면 된다 생각하자. 엄밀하게는 아닌데 소리는 그렇게 생각해도 된다. 그래서 저 부드럽게 0으로 만드는 게 중요하다.
librosa로 구현
import os
import librosa
import librosa.display
import IPython.display as ipd
import numpy as np
import matplotlib.pyplot as plt일단 관련된거 import
jeff_file = "음악 파일 절대 경로"음원을 객체로
ipd.Audio(jeff_file)음원이 맞는지 확인해주자.
jeff, sr = librosa.load(jeff_file)librosa에 로드해주고
FRAME_SIZE = 2048
HOP_SIZE = 1024파라미터 정해주자. 나는 hopsize를 framesize의 절반으로 했다.
S_jeff = librosa.stft(jeff, n_fft=FRAME_SIZE, hop_length=HOP_SIZE)librosa의 stft로 푸리에 변환을 해주자.
S_jeff각 샘플당 주파수 성분이 나온다.
array([[-9.77935852e-05+0.0000000e+00j, -6.74150360e-05+0.0000000e+00j,
1.83536939e-03+0.0000000e+00j, ...,
9.98383272e-04+0.0000000e+00j, -4.79787542e-03+0.0000000e+00j,
-8.87365453e-03+0.0000000e+00j],
[ 7.62030977e-05-6.9481583e-05j, -7.92763080e-04-2.9076386e-04j,
-1.83978374e-03+2.5306887e-03j, ...,
2.19850112e-02+9.3443021e-03j, 1.69387553e-02-2.0108012e-02j,
-1.68905444e-02-1.6665967e-02j],
[ 1.62465676e-05+9.9002573e-05j, 5.35971136e-04-8.3187647e-04j,
2.42920429e-03-2.0759813e-03j, ...,
1.99608374e-02-5.6008119e-03j, -6.67677149e-02-3.9605811e-02j,
-3.32573391e-02+1.0340718e-02j],
...,
[-1.59350311e-05+5.5106744e-07j, 3.16969606e-09+2.0793385e-09j,
1.35053595e-08-1.7429310e-09j, ...,
-4.66316230e-08-3.6616881e-09j, -1.91711780e-09+1.3092157e-08j,
3.10114046e-05+1.4846132e-04j],
[ 1.59371120e-05-2.7579603e-07j, 3.99187661e-09+3.1417899e-10j,
1.68206320e-08+5.0186327e-10j, ...,
-4.66403876e-08-4.1961989e-09j, 1.41498591e-08-1.5359999e-09j,
-9.56016811e-05+1.1761385e-04j],
[-1.59373885e-05+0.0000000e+00j, 3.47596929e-09+0.0000000e+00j,
1.44067576e-08+0.0000000e+00j, ...,
-4.82346110e-08+0.0000000e+00j, 1.65743383e-08+0.0000000e+00j,
-1.51537286e-04+0.0000000e+00j]], dtype=complex64)
이렇게 나오는 데 값이 상당히 작음을 알 수 있다.
Y_scale = np.abs(S_jeff) ** 2저번 시리즈에서 크기는 제곱으로 표현한다고 했다.
def plot_spectrogram(Y, sr, hop_length, y_axis="linear"):
plt.figure(figsize=(25, 20))
librosa.display.specshow(Y,
sr=sr,
hop_length=HOP_SIZE,
x_axis="time",
y_axis=y_axis,
)
plt.colorbar(format="%+2.f")그림을 그려주는 함수를 정의하자.
plot_spectrogram(Y_scale, sr, HOP_SIZE, "linear")그려주면

밑에 있긴한데 정말 안보인다. 지금 선형적이라 그렇다 값을 확인하면
array([[9.56358548e-09, 4.54478721e-09, 3.36858079e-06, ...,
9.96769131e-07, 2.30196092e-05, 7.87417448e-05],
[1.06346016e-08, 7.13016902e-07, 9.78918888e-06, ...,
5.70656732e-04, 6.91253575e-04, 5.63044916e-04],
[1.00654622e-08, 9.79283413e-07, 1.02107324e-05, ...,
4.29804117e-04, 6.02654740e-03, 1.21298095e-03],
...,
[2.54228916e-10, 1.43706237e-17, 1.85432532e-16, ...,
2.18791617e-15, 1.75079884e-16, 2.30024728e-08],
[2.54067600e-10, 1.60337861e-17, 2.83185534e-16, ...,
2.19293378e-15, 2.02577803e-16, 2.29726975e-08],
[2.54000349e-10, 1.20823625e-17, 2.07554664e-16, ...,
2.32657780e-15, 2.74708693e-16, 2.29635493e-08]], dtype=float32)
이렇게 매우 작은 값이라 그렇고 로그 스케일로 변환해서 크게 보자고
librosa.power_to_db을 이용해주자.
스펙트로그램의 power를 데시벨로 바꿔준다.
Y_log_scale = librosa.power_to_db(Y_scale)
plot_spectrogram(Y_log_scale, sr, HOP_SIZE)실제 데시벨로 표현한건 다음과 같다.
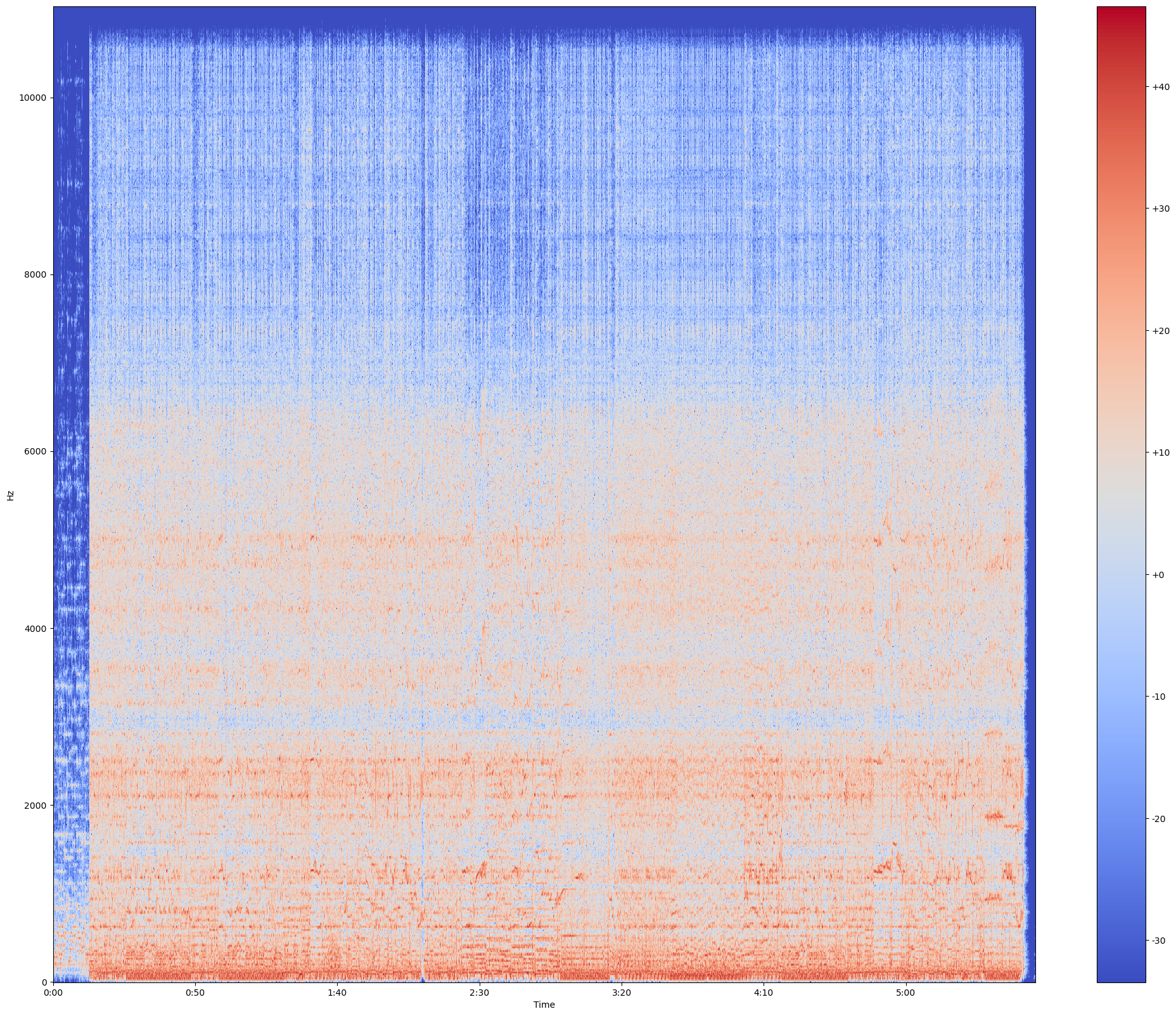
잘 보이지? 시간이 세밀하게 지금 5분 넘어서 그렇지 실제로 짧은 음원으로 보면 특징을 잘 확인 할 수 있다.
