✏️ SVM (Support Vector Machine)

✏️ 선형 SVM

✏️ 마진과 서포트 벡터

SVM은 두 클래스를 나누는 최적의 직선(고차원의 경우 초평면)을 찾는 것을 목표로 한다. 이를 위해 데이터 포인트와 분류 선 사이의 거리를 최대화하려 한다. 이 거리를 마진(margin)이라고 하며, 마진을 구성하는 데이터 포인트를 서포트 벡터(support vector)라고 한다.

• 마진: 분류 선과 가장 가까운 데이터 포인트 사이의 거리.
• 서포트 벡터: 마진을 구성하는 데이터 포인트.

✏️ 최대 마진 초평면

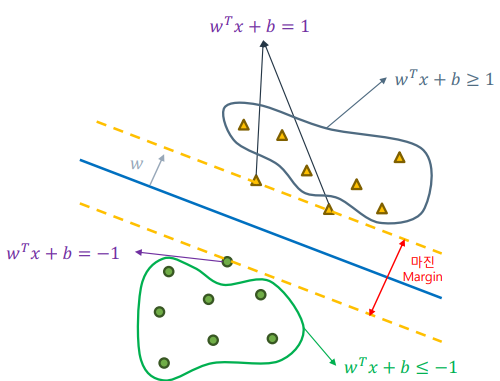
SVM의 목적은 마진을 최대화하는 최적의 직선을 찾는 것이다. 이를 위해 다음과 같은 선형 방정식을 사용한다:

[ $w \cdot x + b = 0$ ]

여기서 ( w )는 최대 마진 초평면의 법선 벡터, ( b )는 편향값이다. 서포트 벡터는 다음 조건을 만족한다:

[ $w \cdot x_i + b \geq 1 \text{ for } y_i = 1$ ]
[ $w \cdot x_i + b \leq -1 \text{ for } y_i = -1$ ]

이를 하나의 식으로 표현하면 다음과 같다:

[ $y_i (w \cdot x_i + b) \geq 1$ ]

마진은 다음과 같이 표현할 수 있다:

[ $\text{Margin} = \frac{2}{\|w\|}$ ]

✏️ 최적화 문제

SVM의 목표는 마진을 최대화하고 모든 데이터를 올바르게 분류하는 것이다. 이를 수식으로 나타내면 다음과 같다:

[ $\max_{w, b} \frac{2}{\|w\|}$ ]
[ $\text{subject to } y_i (w \cdot x_i + b) \geq 1 \text{ for all } i$ ]

이를 더 간단히 쓰면 다음과 같은 최소화 문제로 표현할 수 있다:

[ $\min_w \frac{1}{2} \|w\|^2$]

[ $\text{subject to } y_i (w \cdot x_i + b) \geq 1 \text{ for all } i$ ]

이 문제를 해결하기 위해 라그랑주 승수법 및 쌍대 문제 방식을 사용한다.

---

✏️ 하드 마진 SVM과 소프트 마진 SVM

✏️ 하드 마진 SVM

하드 마진 SVM은 모든 데이터를 완벽하게 분리하는 경우에 사용된다. 모든 데이터가 완벽히 분리되는 경우, 어떠한 오분류도 허용하지 않는다.

하지만, 일반적으로 데이터는 어느 정도 섞인 경우가 많다. 따라서 완변학 선형 분리가 불가능한 가능성이 높다.

✏️ 소프트 마진 SVM

실제 데이터는 완벽하게 분리되지 않는 경우가 많다. 소프트 마진 SVM은 어느 정도의 오분류를 허용하면서 일반화 성능을 높인다. 이를 위해 슬랙 변수 ( $\xi_i$ )를 도입하여 마진을 위반한 정도를 수치적으로 나타낸다.

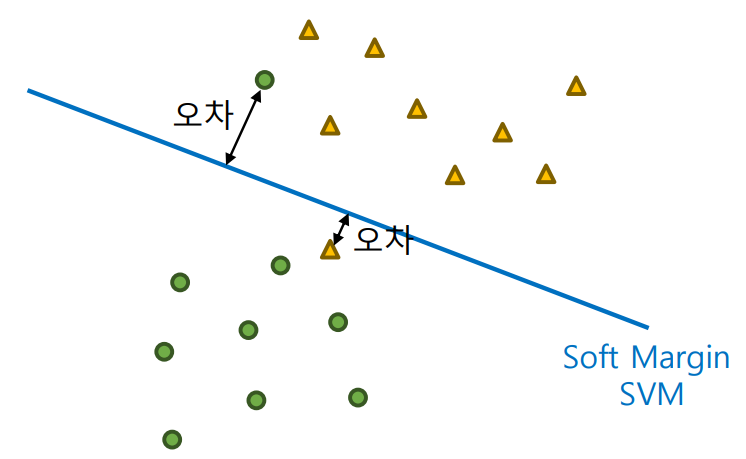
최적화 문제는 다음과 같이 표현된다:

[ $\min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{N} \xi_i$ ]

$\xi_i$(슬랙 변수):

• 각 데이터 포인트 당 하나의 슬랙 변수가 할당되며, 이 변수는 해당 데이터 포인트가 마진을 얼마나 위반했는지 수치적으로 나타낸다.

• 마진을 위반하지 않은 데이터: $\xi_i =0$

• 마진을 위반한 데이터: $0< \xi_i\leq1$

[ $\text{subject to } y_i (w \cdot x_i + b) \geq 1 - \xi_i \text{ and } \xi_i \geq 0$ ]

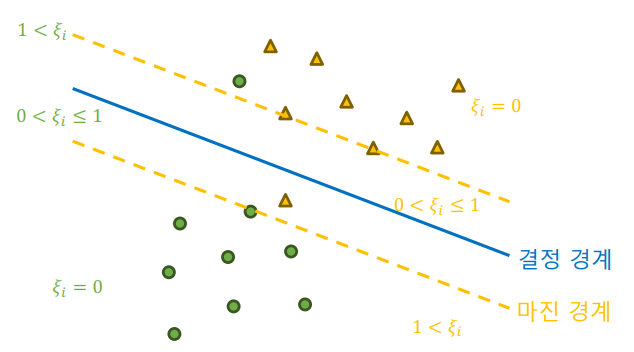
소프트 마진 SVM은 하드 마진 SVM 최적화 과정에 규제 페널티( $C$ )를 도입한다.
여기서 ( $C$ )는 규제 강도를 조절하는 하이퍼파라미터로, 마진 크기와 규제 사이의 중요도를 조절한다. ($C$) 값에 따라 패널티를 얼마나 크기 적용할지 결정할 수 있다.

• 목적

  • 마진 크기를 최대화
  • 마진 위반을 최소화

---

✏️ 비선형 SVM

✏️ 고차원으로의 변환

데이터가 복잡해질수록 선형 결정 경계로 데이터를 분류할 수 없는 경우가 많다.
데이터가 만약 휘어진 형태로 분포한다면, 선형 SVM으로는 분류할 수 없다.

비선형 SVM은 이러한 데이터에 대해 효과적으로 작동한다.

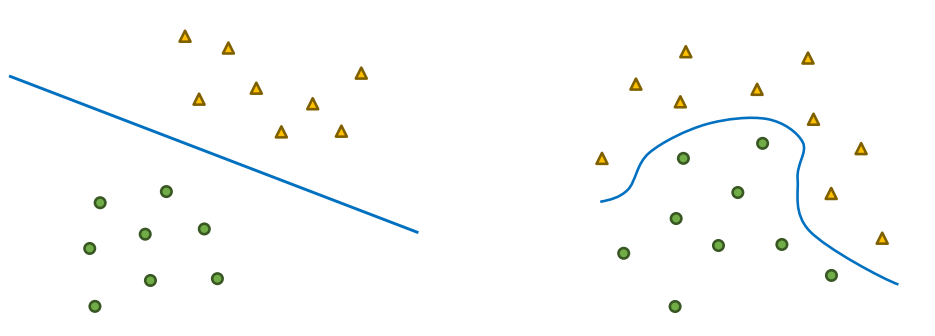
데이터가 선형적으로 분리되지 않는 경우, 데이터를 고차원으로 변환하여 선형 분리가 가능하게 할 수 있다. 이를 위해 매핑 함수 ( $\phi$ )를 사용한다.

다만 고차원의 데이터는 선형 분류 가능성이 높아지지만, 계산량이 늘어나는 단점이 있다. 즉 딜레마에 부딪히게 되는데, 이를 해결하기 위해 커널트릭을 사용한다.

✏️ 커널 트릭 (Kernel Trick)

고차원 변환을 직접 수행하지 않고, 커널 함수를 사용하여 고차원 변환의 내적 연산 결과를 효율적으로 계산할 수 있다. 대표적인 커널 함수는 다음과 같다:

• 다항 커널 (Polynomial Kernel):
  [ $K(x, x') = (\gamma x \cdot x' + r)^d$ ]

  • 입력 벡터의 다항식을 계산하여 변환하는 방식, 과적합 위험이 있다.

• RBF 커널 (Radial Basis Function Kernel) 또는 가우시안 커널 (Gaussian Kernel):
  [ $K(x, x') = \exp(-\gamma \|x - x'\|^2)$ ]

  • 입력 벡터 간의 거리를 기반으로 유사도를 계산
  • 데이터 포인트가 중심에서 얼마나 떨어져 있는지를 반영
  • 유연성이 높아 범용성이 높음

• 시그모이드 커널 (Sigmoid Kernel):
  [ $K(x, x') = \tanh(\gamma x \cdot x' + r)$ ]

  • 신경망에서 사용되는 활성화 함수와 유사한 방식으로 데이터를 변환
  • 이진 분류에 최적화되며 RBF 커널에 비해 성능이 떨어짐

비선형 SVM의 최적화 문제는 다음과 같다:

[ $\min_{w, b, \xi} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{N} \xi_i$ ]
[ $\text{subject to } y_i (w \cdot \phi(x_i) + b) \geq 1 - \xi_i \text{ and } \xi_i \geq 0$ ]

여기서 ( $\phi(x)$ )는 고차원으로의 변환을 나타내며, 커널 함수를 통해 효율적으로 계산된다.

---

✏️ SVR (Support Vector Regression)

SVR은 회귀 문제로 확장한 SVM 방법으로, 주어진 데이터에서 가능한 많은 데이터 포인트를 포함하는 마진 구역을 설정한다. 이 마진 구역은 사용자가 선언한 허용 오차 ( $\epsilon$ ) 내부의 구역이다.

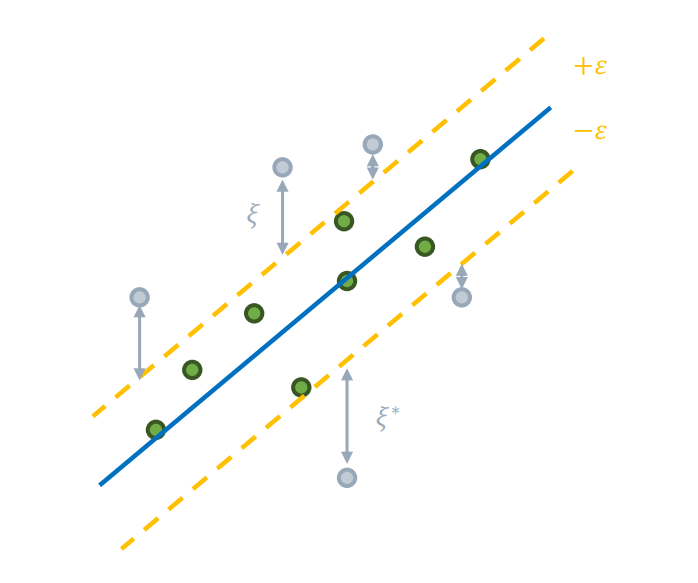
최적화 문제는 다음과 같다:

[ $\min_{w, b, \xi, \xi^*} \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{N} (\xi_i + \xi_i^*)$ ]
[ $\text{subject to } y_i - (w \cdot \phi(x_i) + b) \leq \epsilon + \xi_i$ ]
[ $(w \cdot \phi(x_i) + b) - y_i \leq \epsilon + \xi_i^*$ ]
[ $\xi_i, \xi_i^* \geq 0$ ]

• ( $\epsilon$ )이 바로 정답과 예측값 사이의 차이가 된다.
• 직선 양쪽 방향의 슬랙 변수를 도입해 많은 데이터 포인트가 포함되도록 강제한다.