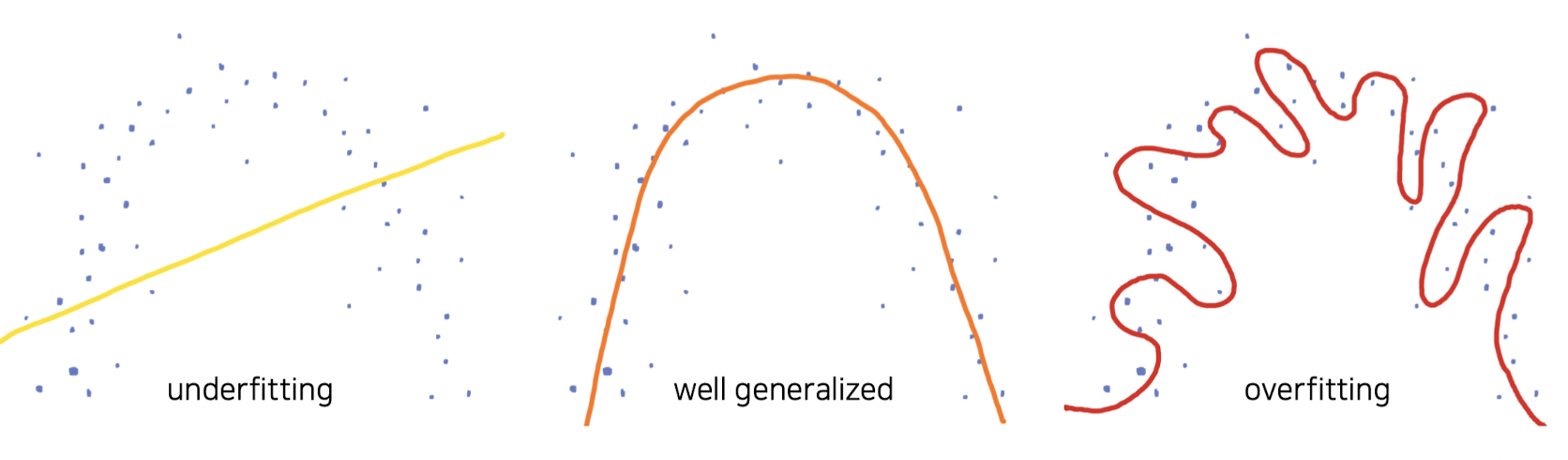
Overfitting
Overfitting (과적합)은 모델이 학습 데이터셋을 지나치게 학습(bias, noise까지) 하여 발생하는 문제로 학습 데이터셋에서는 성능이 높게 나타나지만, 평가 데이터셋(일반화된 데이터셋)에서 오히려 성능이 더 떨어지는 현상을 의미한다. 무조건 나쁜 현상은 아니고 모델의 capacity를 확인하는 하나의 방법이 될 수도 있다.
Overfitting이 발생한다면 훈련데이터를 추가하거나 더 작은 모델을 활용해볼 수 있다. 또한, Dropout, Early Stopping Rule 등등의 정규화 방법론을 활용하기도 한다.
정규화 방법론 (Regularization)
Overfitting을 피하기 위해 generalization error을 낮추기 위한 방법론
1. Norm penalty
Parameter Norm Penalty는 L1 Norm, L2 Norm등이 있으며 손실함수에 해당 Norm Penalty Term을 추가적으로 활용하여 정규화를 진행한다. L1 Norm은 오차의 절댓값을, L2 Norm은 오차 제곱합을 활용한다.
L2 Loss는 오차의 제곱을 더하기 때문에 Outlier에 더 큰 영향을 받는다. Outlier가 적당히 무시되길 원한다면 L1 Loss, Outlier을 신경써야 하는 경우라면 L2 Loss를 사용하면 좋을 것이다.
Weight Decay
L2 Norm을 통해 weight parameter가 원점에서 멀어지는 것(커지는 것)을 방지
- weight parameter는 노드와 노드 간의 관계를 나타냄 (숫자가 커질 수록 강한 관계)
- 전체적인 관계의 강도를 제한하여 출력 노드가 다수의 입력 노드로부터 많이 배우지 않도록 제한
- 보통 training error 최소화를 방해하는 형태
- loss가 최소화될 수록 최대화되는 term이 붙음
- 하이퍼 파라미터 𝛼 를 통해 (둘 다 최소화 하려는 과정에서) 두 term 사이의 균형을 조절 - 그런데 너무 강력한 regularization method이기 때문에 쓰이는 일은 거의 없음.
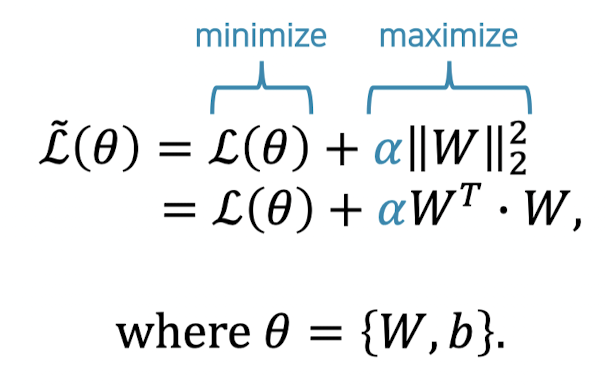
2. Dropout
학습 과정 중 신경망의 뉴런 중 일부를 랜덤하게 부분적으로 생략(turn off)하는 방법론으로 학습이 진행될 때마다 뉴런을 무작위로 학습하여 매번 모델을 다르게 학습시킨다는 관점에서 앙상블 기법과 유사한 효과를 낸다.
- 학습과 추론의 방법이 다름
• 학습 (train) : 확률 𝑝에 따라 노드를 turn-off
• 추론 (test) : 모든 노드를 turn-on
• 학습 때보다 평균적으로 1/p배 더 큰 입력을 받게 될 것
• 따라서 𝑝를 𝑊에 곱하여 이를 상쇄
Model Mode 전환
Loop for n_epochs:
model.train()
Loop for n_mini_batches in train-set:
Feed-forward.
Calculate loss.
Back-propagation.
1 step gradient descent.
model.eval()
Loop for n_mini_batches in validation-set:
Feed-forward.
Calculate loss.
Save model if it is best.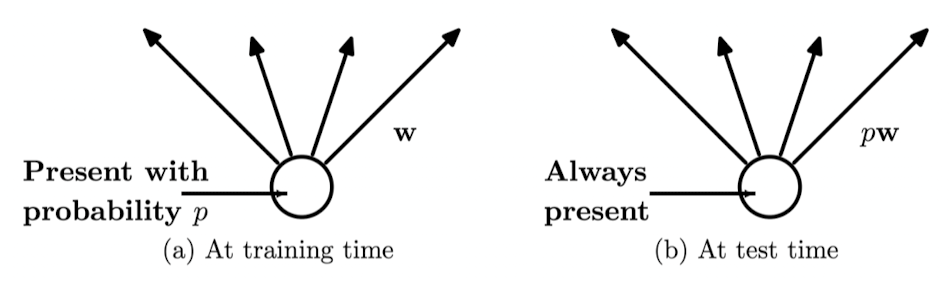
일반적으로 레이어 -> 활성함수 -> 드랍아웃 -> 레이어... 순서
3. 배치 정규화 (Batch Normalization)
배치단위간에 데이터 분포의 차이가 발생할 수 있기에, 학습 과정에서 각 배치 별로 데이터의 평균과 분산을 이용해 정규화를 진행하는 방법론으로 각 데이터 분포를 평균은 0, 표준편차는 1인 데이터의 분포로 조정한다.
정규화 후 scaling + shifting
- Dropout 대체 가능!
- Hyper-parameter의 추가 없이 빠른 학습과 높은 성능 모두 보장!
(쓸 수 있으면 무조건 써야함) - Dropout과 마찬가지로 모델 모드 전환 필요함
- RNN에는 사용할 수 없음 (Layer Normalization 쓰면 됨)
일반적으로 레이어 -> 활성함수 -> 배치 정규화 -> 레이어... 순서
4. Data Augmentation
핵심 특징(feature)를 간직한 채, 입력 데이터에 노이즈를 추가하여 학습 효과를 높이고 과적합을 방지하는 방법론이다.
• 보통은 핵심 특징을 보존하기 위한 휴리스틱한 방법을 사용
• 이를 통해 더욱 noise robust한 모델을 얻을 수 있음
• 규칙을 통해 증강(augment)하는 것은 옳지 않고 Randomness가 필요함
ex1) image -> rotation, flipping, shifting
ex2) text -> dropping, order exchange
• 기존 데이터를 통해 새로운 지식을 배울 수 없다는 한계가 있지만, 최적화 측면에서 좀 더 유리할 수는 있다.
5. Early stopping
마지막으로 Early Stopping은 모델의 과적합을 방지하기 위해서 이전 에폭에 비해 검증 오차(Validation Loss)가 감소하다 증가하는 경우 학습을 종료시키는 방법론이다.
Underfitting
Underfitting(과소적합)은 Overfitting(과적합)의 반대 개념으로 모델이 충분히 학습 데이터를 학습하지 않은 상태를 의미한다. Underfitting이 발생한다면 학습을 더 오래 진행하거나 capacity가 더 큰 모델을 활용하여 문제를 해결 할 수 있다.
