베이즈 정리

베이즈 정리는 조건부 확률에 사전확률(prior)을 활용하여 통계적 추론을 하는 방법이다.
베이지안 분류기
베이즈 정리를 이용하여 분류에 활용한 것이다.
테스트 데이터 x가 있을 때, 이 x가 어떤 class인지 구하기 위해서는 다음과 같은 식을 이용하면 된다.
위 식을 각 class 별로 구하여 테스트 데이터 x가 해당 class일 확률을 계산한 후, 가장 큰 확률을 지닌 class를 택하는 것이다.
이때 분모의 P(x)는 모든 class에 대하여 전부 동일하므로, 생략할 수 있다.
만약 데이터의 feature가 2개라고 가정한다면, 실제로 각 class에 대해 비교하게 될 최종 식은 다음과 같이 정리될 수 있다.
그러나, 데이터 x의 feature들의 교집합이 train data에 존재하지 않았으면, 이에 대한 확률은 0이 되어버린다.
나이브베이즈 분류기
Naive bayes에서 Naive는 확률을 독립으로 가정한다는 의미이다.
즉, 나이브베이즈 분류기는 feature들이 서로 독립이라는 가정을 한다.
따라서, 각각의 feature들에 대해 따로 계산할 수 있게 된다.
만약 데이터의 feature가 2개라고 가정한다면, 실제로 각 class에 대해 비교하게 될 최종 식은 다음과 같이 정리될 수 있다.
그러나, 아예 관측되지 않은 feature값이 들어오게 된다면 이에 대한 확률은 다시 0이 된다.
가우시안 나이브베이즈 분류기
가우시안 나이브베이즈 분류기는 가우시안 분포를 따르는 나이브베이즈 분류기이다.
즉, 각각의 feature에 대해 평균과 표준편차를 구하여, 이에 대한 가우시안 분포를 기반으로 확률을 구하는 것이다.
만약 데이터의 feature가 2개라고 가정한다면, 실제로 각 class에 대해 비교하게 될 최종 식은 다음과 같이 정리될 수 있다.
이때 uki와 σki는 각각 k번째 feature의 i class에 대한 평균과 분산을 의미한다. 즉, N(feature 1;u1i,σ1i)는 새로운 데이터 x의 feature1에 대한 첫 번째 feature들의 가우시안 분포에 따른 값을 의미한다.
그러나 이 모델은 XOR문제를 풀지 못한다는 한계가 있다.
베이지안 네트워크
도메인 지식에 기반한 가설을 바탕으로 한 설계이다. 나이브베이즈도 이를 이용하여 표현할 수 있다.
이 모델은 일반적이고 직관적이라는 장점이 있다.
클래스와 feature (또는 feature들 간의) 사이에 임의의 edge를 생성하고, 빈도수를 기반으로 베이지안네트워크의 각 노드에 대해 확률계산을 함으로써 분류가 가능해진다.
이때 그래프는 화살표가 있는 direct edge로 표현한다. 만약 화살표가 없으면 이는 두 노드간의 관계가 독립임을 의미하므로 주의해야 한다.
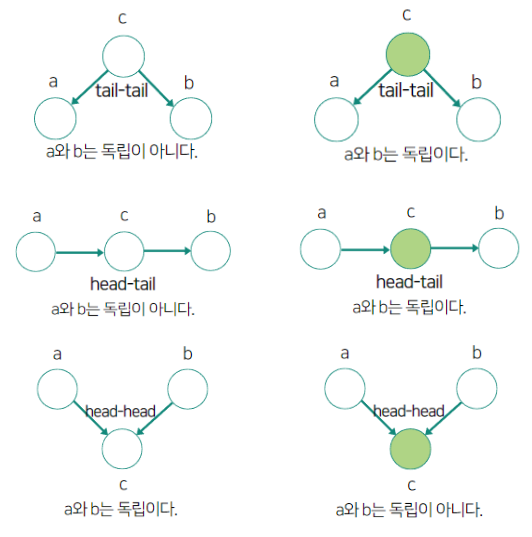
색이 칠해져 있는 노드는 이미 확률값이 결정되어있음을 의미한다.
위 그림을 의미하는 것은 생각보다 직관적으로 이해할 수 있다.
맨 위쪽의 tail-tail일 때를 보자. 노드 c값이 결정되어 있지 않다면, c값에 따라 a와 b의 값이 결정되므로 a와 b가 독립이 아니다.
그러나 c값이 결정되어 있다면, a와 b에 미치는 영향이 이미 결정되어 있는 것이므로 a와 b가 독립이 된다.
그 다음으로 head-tail일 때를 보자. 노드 c값이 결정되어 있지 않다면, a에 값에 따라 c값이 영향을 받고, 또 이 c값에 따라 b값이 영향을 받는다. 따라서 a와 b는 독립이 아니다.
그러나 c값이 결정되어 있다면, a가 어떤 값이 되든, a에 대한 값의 변화가 b에 영향을 주지 않는다. 따라서 a와 b는 독립이 된다.
마지막으로 head-head일 때를 보자. 노드 c값이 결정되어 있지 않다면, a와 b 둘 다 c의 값에 영향을 줄 수 있다. c 값이 아직 결정이 안 되어 있으므로, a와 b값에 따라 그대로 c 값이 결정된다. 따라서 a와 b는 독립이 된다.
그러나 c값이 결정되어 있다면, a가 특정값으로 정해지면 b값은 이에 따라 자동으로 결정되게 된다. 따라서 a와 b는 독립이 아니다.
이러한 베이지안 네트워크를 이용하면 XOR 문제도 풀 수 있다.

