선형 분류와 회귀

Cammie·2022년 6월 30일

LASSO regression Linear Regression Logistic Regression Ridge Regression machine learning 머신러닝

머신러닝

목록 보기

4/7

선형회귀(Linear regression)

학습과정

임의의 파라미터 값을 설정해서 선형모델을 가정한다.
train data로 학습한다.
loss, cost를 사용해서 MSE를 구한다.
경사하강법을 사용해서 MSE가 가장 작은 파라미터를 찾는다. (Least Squares methods; 최소 제곱법)

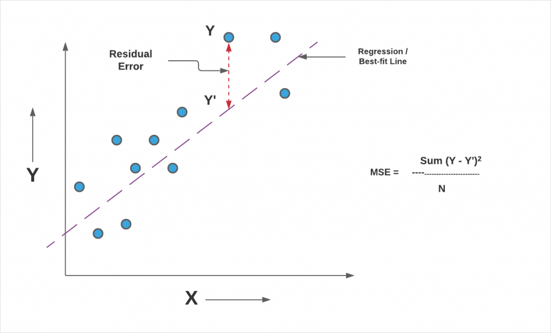
이미지 출처: https://vitalflux.com

loss는 실제값과 예측값 차이(오차)를 제곱한 것(SE; Squared Error)이다.

loss = (Y-Y')^2

이때 Y는 실제값을 의미하고, Y'는 예측값을 의미한다.

cost는 오차제곱들의 평균(MSE; Mean SE)이다.

MSE=\frac{1}{N}\sum_{i=1}^N (Y_i-Y_i')^2

이때 다중 선형회귀 모형의 식은 다음과 같다.
(다중 선형회귀란 독립변수 x가 여러개가 있는 선형회귀이다.)
$\sum_{i=1}^n 𝑦_𝑖 = \sum_{i=1}^n (\beta_0 + \sum_{j=1}^p\beta_jx_{ij} + \epsilon_𝑖) , \qquad 𝑖 = 1, 2, ..., 𝑛, \epsilon_𝑖~𝑁(0, \sigma^2)$
따라서 회귀계수의 추정은 경사하강법을 이용하여 오차항인 𝜖𝑖의 제곱을 최소로 하는 값을 찾는 것이다.
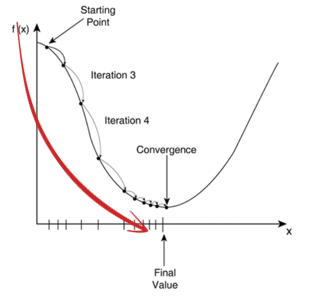
$\sum_{i=1}^n \epsilon_𝑖^2 = \sum_{i=1}^n (𝑦_𝑖-\beta_0 - \sum_{j=1}^p\beta_jx_{ij})^2$

경사하강법(Gradient Descent)은 MSE 함수식을 최소화하기 위한 값을 찾는 방법으로, 미분으로 기울기를 구해서 조금씩 하강시키며 최적의 값을 찾는다.

새로운값=기존값-러닝레이트\times 미분결과

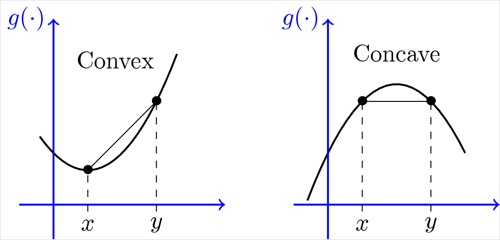
참고로 convex는 (아래로) 볼록한 함수를 의미하며, concave 오목한 함수를 의미한다.

Ridge regression

선형회귀에서 파라미터가 너무 커지지 않도록(즉, 과적합되지 않도록) L2 norm을 사용해서 제한한다.

이때, norm은 벡터의 크기(magnitude)를 측정하는 방법이다.

L2 norm

유클리드 노름이라고도 한다.

이 L2 norm은 다음과 같이 계산된다.
$L_2=||x||_2=\sqrt{\sum_i^nx_i^2} = \sqrt{\sum_i^nx_i\cdot x_i} = \sqrt{\sum_i^nx_i^T x_i}$

위의 L2 norm을 선형회귀 추정을 위한 비용함수인 오차항의 제곱식에 추가하면 최종 릿지 회귀식이 된다.

\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2+\lambda\sum_{j=1}^p\beta_j^2

그러면 이러한 Ridge regression이 어떻게 과적합을 막을까?

위 식을 살펴보면 릿지회귀의 식은 기존의 비용함수 $\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2$ 에 람다를 곱한 L2 norm 을 더한 것이다.

이때 람다는 0에서 1 사이의 값을 갖는데, 이 람다의 값이 커질수록 비용함수의 변화가 줄어들게 되는 Regularization이 일어나게 된다. 즉, $\lambda\sum_{j=1}^p\beta_j^2$ 값을 regular term으로 보게 되며, 이때 람다가 클수록 제한이 강해지는 것이다.

Lasso regression

과적합을 막기위해서 L1 norm을 사용하는 방법이다.

L1 norm

맨허튼 노름이라고도 한다.

이 L1 norm은 다음과 같이 계산된다.
$||x||_1=\sum_{i=1}^n|x_i|$

이 방법은 절대값을 이용하였으므로 미분이 불가능하기에 경사하강법이 아닌 다른 방법으로 최적화를 해야한다.

따라서 라쏘 회귀의 식은 다음과 같다.

\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij})^2+\lambda\sum_{j=1}^p|\beta_j|

Lasso regression의 경우 중요하지 않은 feature에 대해 weight 값을 0으로 둔다. 즉, feature selection효과도 있다.

또한, 절대값을 사용하기 때문에 Ridge regression보다 더 타이트하게 Regularization이 일어난다.

Logistic Regression

Logistic regression은 "regression"이라고 명시되어 있지만, "classification"문제를 풀기위한 모델이다. 헷갈릴 수 있으므로 잘 기억해야 한다.

Logistic regression은 선형 회귀를 이용하여 선형 분류를 하는 모델이다.

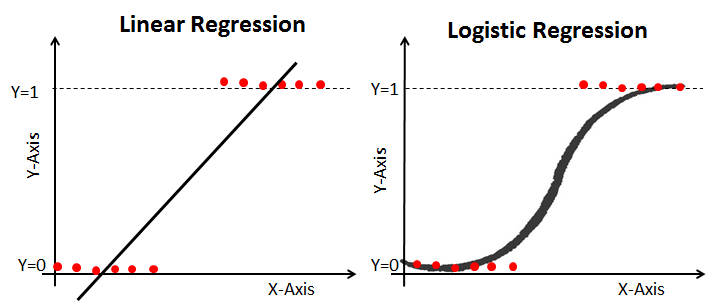
이미지 출처: https://nittaku.tistory.com/478

위와 같이 데이터의 형태인 경우, 선형회귀로는 이를 예측하기 힘들다. 따라서 이를 곡선으로 만들어 주어 회귀식으로 이진분류를 가능하게 만든다. 이때 이렇게 로지스틱 함수와 같이 s자형으로 표현되는 곡선 함수들을 통틀어 시그모이드 함수라고 한다. (그러나 일반적으로 시그모이드 함수라 하면 로지스틱 함수를 의미한다.)

이러한 로지스틱 회귀를 하기위한 과정은 다음과 같다.

오즈비(odds ratio)를 구한다.
$Odds(P)=\frac{P}{1-P} = \frac{A일\,확률}{A가\,아닐\,확률}$
오즈비에 로그함수를 취한다. 이를 로짓 함수(Logit function)라고 한다.
$logit(P)=log(\frac{P}{1-P}) = e^z = wx+b$
logit 함수를 P에 대해 역변환을 한다. 이를 로지스틱 시그모이드 함수(Logistic Sigmioid function)라고 한다.
$P(x)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(wx+b)}}$
이때 이 wx+b 는 선형합을 의미한다. 따라서 이 z에 최적화된 선형합이 들어가게 되면 해당 데이터 x에 대해 A일 확률값이 나오게 되는 것이다.

이때 최적화된 선형합을 구하는 수식은 다음과 같은 방법으로 계산된다.

argmax\prod P(label|x)=\prod\frac{1}{1+e^{-label\times(wx+b)}}

이때 label값은 A인 경우 1, A가 아닌 경우 -1로 설정한다. 따라서 부호가 항상 같게 유지가 되어 어떤 데이터가 들어오든지 전부 최대화를 가능하게 만든다.

그러나 이 식을 최대화를 하는 식이며, 곱셈들로 이루어졌으므로 경사하강법을 이용할 수 없다.

따라서 위 식에
① 로그를 씌워 곱셈들을 덧셈 연산으로 변환되게 하며,
② 부호를 바꾸어 최소화를 시키는 식으로 바꾸어 준다.

\sum -log\frac{1}{(1+e^{-label\times(wx+b)})}=\sum log(1+e^{-label\times(wx+b)})

위 식에 경사하강법을 이용하여 최적의 파라미터 값을 찾으면 된다.

따라서 logistic function 값이 0.5보다 큰지, 작은지에 따라 데이터 레이블을 결정을 한다.

++ 참고로 이진분류가 아닌 label 개수가 3개 이상일 때 사용하는 다항 로지스틱회귀라는 모델이 있다.

부가적인 내용들

Q. 왜 경사하강법과 같이 iterative(반복적인) 방법으로 학습할까?

A. 많은 양의 데이터를 학습할 때에는, 한번에 바로 최적화시키기가 어렵다. 따라서 최적화를 하기 위해 반복적인 학습과정을 거치는 것이다.

Classification vs Regression

분류는 예측하려는 목적값이 label, 회귀는 예측하려는 목적값이 real-number이다.
분류, 회귀 둘 다 지도학습이다.

Linear Classification vs Linear Regression

선형 분류는 0~1사이의 확률값 생성한다. 따라서 이때의 임계치값을 정하여, 이를 기준으로 분류한다.
선형 회귀는 0~1이외의 값들이 나온다. 즉, 확률값이 아니므로 분류 문제들에 적합하지 않다.

Cammie

이전 포스트

베이지안 네트워크 (BAYESIAN NETWORKS)

다음 포스트