N412. 경사하강법과 역전파 알고리즘

ssu_hyun·2021년 11월 4일

AI Bootcamp ML/DL

[codestates] AI Bootcamp

목록 보기

38/62

🏆 학습목표

경사 하강법(Gradient descent)과 역전파(Backpropagation)에 대해 이해하고 설명할 수 있다.
경사하강법과 역전파 알고리즘을 사용하여 신경망을 구현할 수 있다.
케라스(Keras) 프레임워크를 이용하여 모델을 구축할 수 있다.

순전파

: 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서 값을 내보내는 과정

1. 입력층으로부터(혹은 이전 은닉층으로부터) 신호(데이터)를 전달받는다.
2. 입력된 데이터를 가중치 및 편향과 연산한 뒤에 더해준다.(가중합, weighted sum)
3. 가중합을 통해 구해진 값은 활성화 함수(Activation function)를 통해 다음 층으로 전달된다.

특정 층에 입력되는 데이터의 특성이 $n$ 개인 경우 위 과정을 수식으로 나타내면 다음과 같다.

y = \text{sigmoid}\bigg(\sum( b + w_{1}x_{1} + w_{2}x_{2} + ... + w_{n}x_{n})\bigg)

신경망 학습 알고리즘 요약

데이터와 목적에 맞게 신경망 구조 설계
- 입력층 노드(유닛) 수 = 데이터의 Feature 수
- 출력층 노드(유닛) 수 = 문제(분류, 회귀 등)에 따라 다르게 설정
- 은닉층 수와 각 은닉층의 노드 수 결정

가중치 랜덤하게 초기화
순전파
비용 함수(Cost function) 계산
역전파 통해 각 가중치에 대한 편미분 값 계산

경사하강법을 사용하여 비용함수를 최소화하는 방향으로 가중치 갱신
중지 기준을 충족하거나 비용 함수를 최소화 할 때까지 2-5 단계 반복하며
이를 한 번 진행하는 것을 iteration 이라고 함

👑역전파(Backpropagation)

비용(cost), 손실(loss)/에러(error) 함수 계산

신경망의 성능을 측정하기 위해서 비용함수 $J(x)$ 를 계산해야 한다.
한 데이터 샘플을 Forward Propagation 시키고
마지막 출력층을 통과한 값과 이 데이터의 타겟값을
비교하여 loss 혹은 error를 계산한다.

한 데이터 포인트에서의 손실 : loss
전체 데이터 셋의 loss를 합한 개념 : cost

최종목적은 이 오차에 관한 함수 $E$ 의 함수값을 0에 근사시키는 것이다.
오차가 0에 가까워진다면, 신경망은 학습에 사용된 input들과 그에 유사한 input에 대해서 우리가 원하는 output,
즉 정답이라고 할 수 있는 값들을 산출할 것이다.

대표적인 손실함수로는 MSE, Cross-Entropy 등이 있다.

역전파
: 매 iteration마다 손실(Loss or Error) 정보를 출력층에서 입력층까지 전달하여 구해진 손실을 줄이는 방향으로 가중치를 얼마나 업데이트 해야할지 결정하는 알고리즘

경사 하강법
: 손실을 줄이는 방향을 결정하는 것

경사하강법

역전파(Backpropagation, BP)

구해진 손실 정보를 출력층부터 입력층까지 전달하여 각 가중치를 얼마나 업데이트 해야할지를 결정하는 알고리즘
Backpropagation = "Backwards Propagation of Errors" 의 줄임말

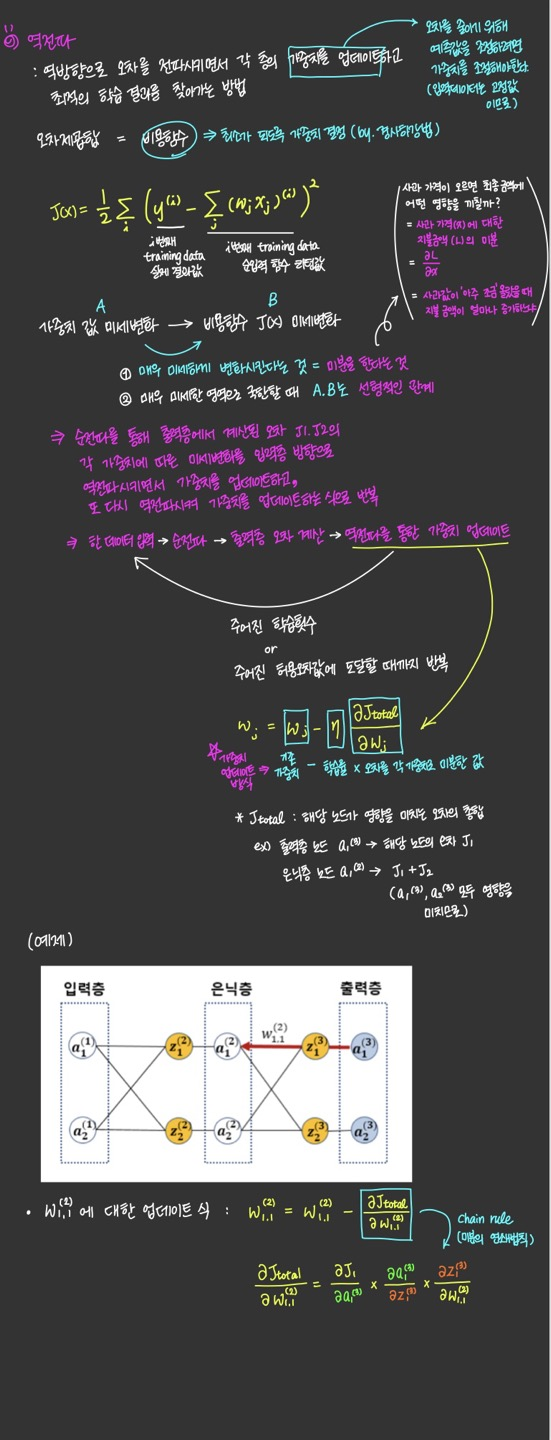
위 식의 오른쪽 항에 있는 3개의 미분값을 하나하나 구해보면 아래와 같다.

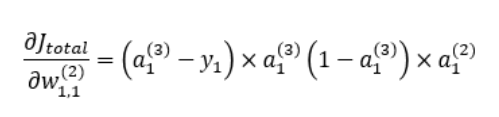
역전파에서 가중치 업데이트를 위해 사용되는 오차의 가중치에 대한 미분값이
결국 역전파의 출발 노드의 활성 함수 값과 도착 노드의 활성 함수 값, 그리고 실제값만으로 표현되는 것을 알 수 있다.

위 식의 오른쪽 항에서 처음 두 식의 값을 아래와 같이 $\delta_1^{(3)}$ 으로 둔다.

역전파에 의해 업데이트 되는 $w_{1,1}^{(2)}$ 와 $w_{1,2}^{(2)}$ 는 다음과 같다.

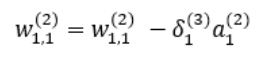
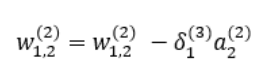
$\delta_2^{(3)}$ , $w_{2,1}^{(2)}$ 와 $w_{2,2}^{(2)}$ 은 아래와 같다.

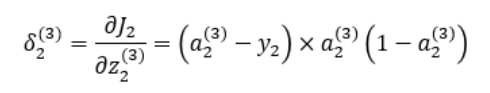
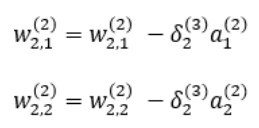
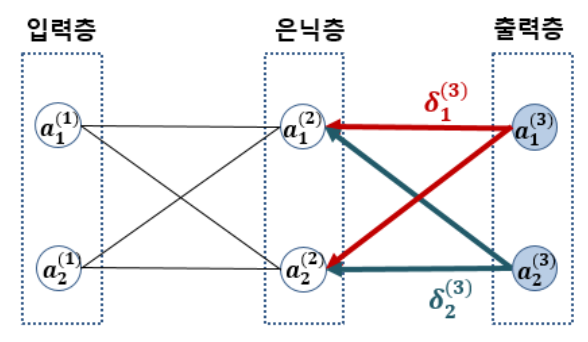
지금까지 다룬 역전파 알고리즘 개념을 그림으로 도식화하여 나타내보면 다음과 같다.
이와 같이 순전파 -> 역전파 -> 가중치 업데이트 -> 순전파 ...로 계속 반복해나가면 오차값이 0에 가까워지게 된다.

👩‍🏫초등학생에게 역전파 설명해보기

신경망은 우리의 뇌 구조와 같다고 생각하면 됩니다. 조금 이해하기 쉽도록 예시를 들어 설명하도록 하겠습니다.
우리가 자전거를 처음 타본다고 가정을 해보겠습니다. 당연히 처음에 완벽하게 자전거를 타는 것이 불가능하겠죠??
처음에는 페달을 밟기 전에도 쓰러진다던지, 잘 나가다가도 중심을 잡지 못해 넘어진다던지 수많은 실패를 거듭할 것입니다.
여기서 완벽하게 자전거를 타는 것=완성, 넘어지거나 쓰러져 완벽하게 자전거를 타지 못하는 것=실패라고 해보겠습니다.
우리의 뇌는 계속해서 완성에 가깝게 가기위해 여러번의 실패를 거듭하며 그 속에서 완성과 실패의 차이를 매꾸기 위해 여러 시도들을 할 것입니다.
그렇게 된다면 언젠가는 결국 완성과 실패의 차이 즉, (완성-실패) = 0 이 되어 완성에 도달하게되고 완벽하게 자전거를 탈 수 있을 것입니다.

신경망도 이러한 원리와 같다고 생각하면 됩니다.
신경망은 어떠한 정답(레이블)이 정해져 있는 문제(데이터)를 입력층에서 입력받아 은닉층에서 (가중치, 편향의) 연산을 하여 출력층에 어떠한 자신만의 답을 도출해내게 됩니다.
=> 여기까지의 과정을 '순전파'라고 말합니다.

신경망은 자신의 답이 틀렸는지 맞았는지, 틀렸다면 어느 정도의 차이가 나는지를 계산하기위해 원래 정해져 있던 정답(레이블)과의 오차를 계산합니다.
=> 이는 위 예시에서 자전거 타는 것을 시도하였을 때 넘어지든, 쓰러지든 어떤 결과가 나왔고 (완성-실패)의 차이가 생긴 것을 의미합니다.

신경망은 이 오차를 0에 가깝게 줄이기 위해 어떠한 방식을 시도하는데 이것이 바로 "역전파(Backpropagation)"입니다.
신경망의 오차는 어떠한 함수, 그래프로 나타낼 수 있고 그 함수, 그래프의 최소값을 찾기 위해 다양한 방법(경사하강법)을 시도합니다.
=> 다음에 자전거를 탔을 때는 완성에 가까워질 수 있도록 다리에 힘을 준다던지, 몸의 중심을 잡아본다던지 등의 다양한 시도를 해보는 것과 같게 볼 수 있습니다.

정리하자면 순전파를 통해 신경망이 어떤 답을 내놓았고 그 값을 정답(레이블)과 비교하여 오차를 계산한 후에 이 오차를 최소화하기위해
순전파와는 반대방향으로 가면서 신경망 연산에 영향을 미쳤던 원래 가중치들의 값들을 변화시키고(가중치 업데이트)
(신경망이 내놓은 답(예측값)은 입력데이터와 가중치의 영향을 받는데 여기서 입력데이터는 고정된 값으로 변화시킬 수 없으므로 가중치를 조절해야만 합니다.)
(더 자세히 말하면 "기존 가중치 값 - 학습률x오차를 각 가중치로 미분한 값"을 통해 가중치를 변화시킵니다.)
신경망은 이러한 과정을 정해진 학습횟수(EPOCH) 또는 주어진 허용오차값에 도달할 때까지 반복하여 오차를 최소로 만들고 결국 예측을 정답과 가깝게 할 수 있을 정도의 수준까지 학습하게 됩니다.
=> 다양한 시도들을 통해 점점 자전거를 잘 타는 방식을 익히게되고 거듭된 반복을 통해 결국에는 완성(자전거를 잘 타는 것)에 이르게 되는 것을 의미합니다.

[reference]

옵티마이저(Optimizer)

지역 최적점에 빠지게 되는 문제를 방지하기 위한 알고리즘
경사를 내려가는 방법을 결정하는 것

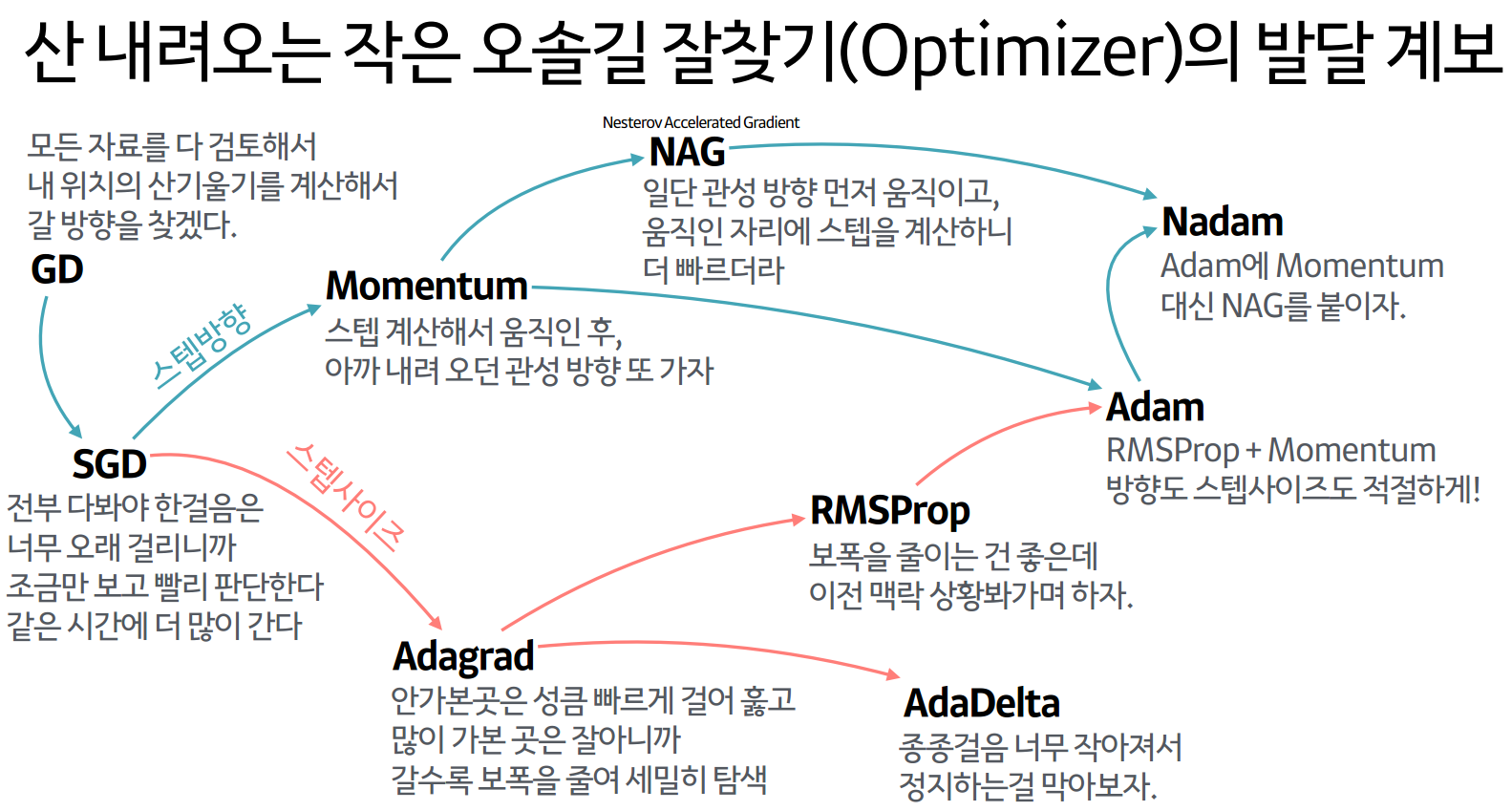
확률적 경사 하강법(Stochastic Gradient Descent, SGD)

전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산하고 그 손실 정보를 역전파하여 신경망의 가중치를 업데이트
1개의 데이터만 사용하여 손실을 계산하기 때문에 가중치를 빠르게 업데이트할 수 있다는 장점이 있지만 동시에 1개의 데이터만 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다는 단점도 있다.

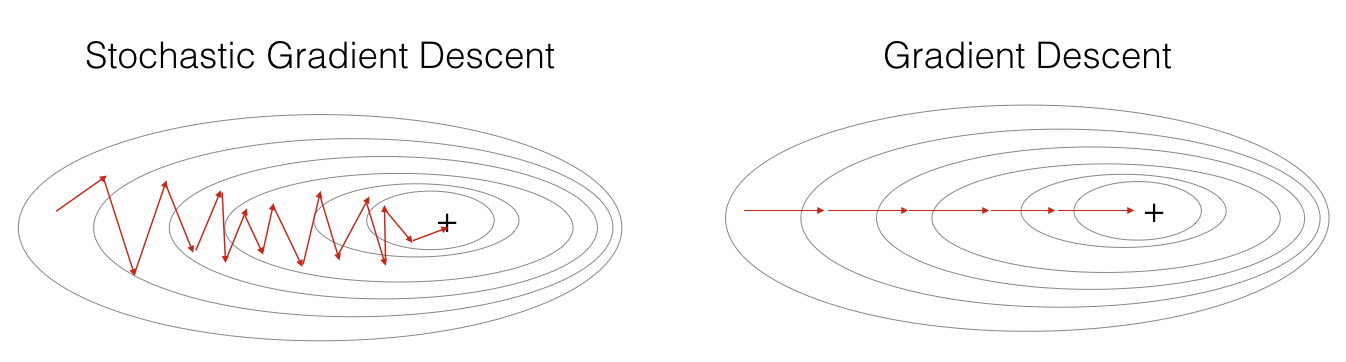
그래서 두 방법을 적절히 융화한 미니 배치(Mini-batch) 경사 하강법이 등장하게 되었다.

미니 배치(Mini-batch) 경사 하강법

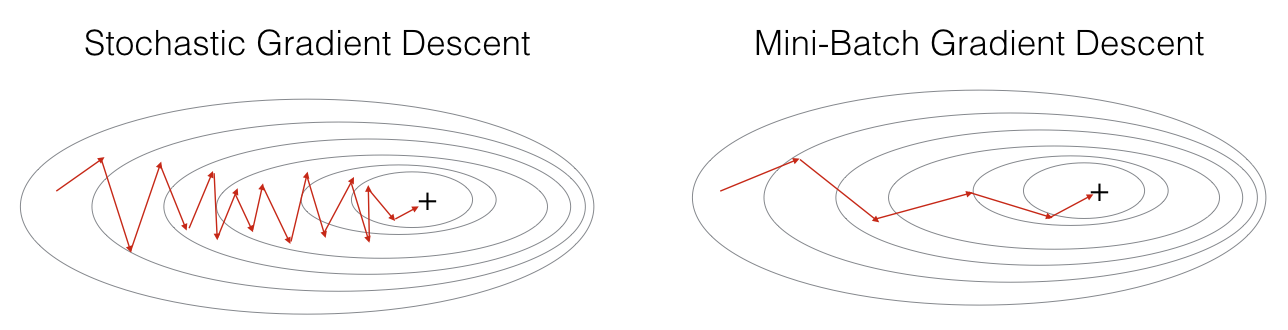
N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치를 업데이트

경사하강법의 변형들(다양한 Optimizer)

확률적 경사 하강법(Stochastic Gradient Descent, SGD)
확률적 경사 하강법(SGD)를 변형한 알고리즘 - Momentum, RMSProp, Adam 등
Newton's method 등의 2차 최적화 알고리즘 기반 방법 - BFGS 등

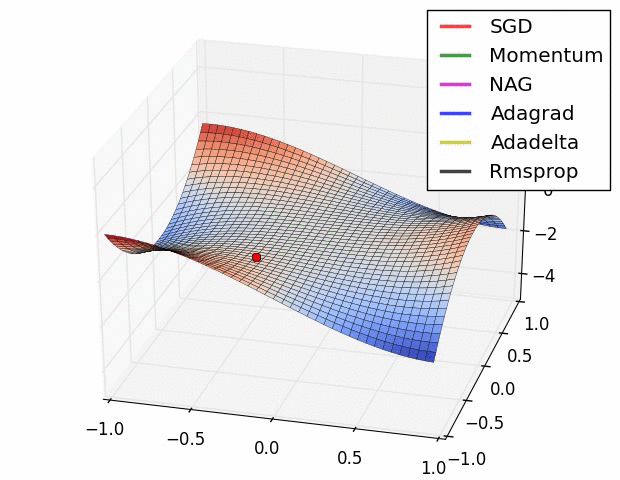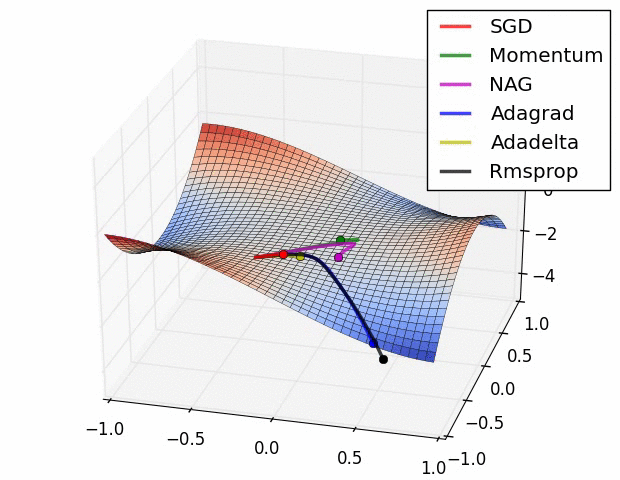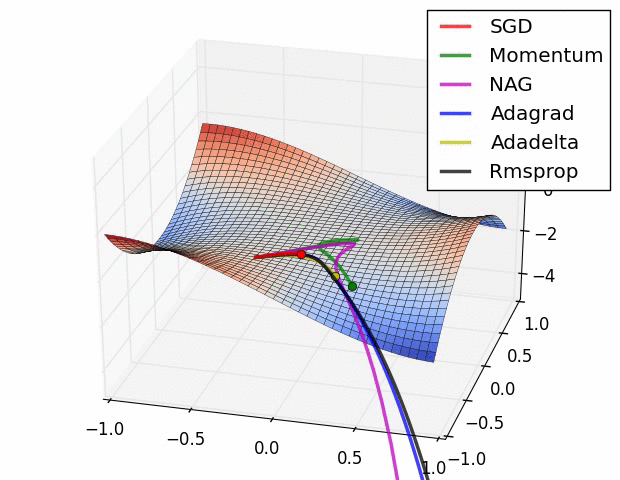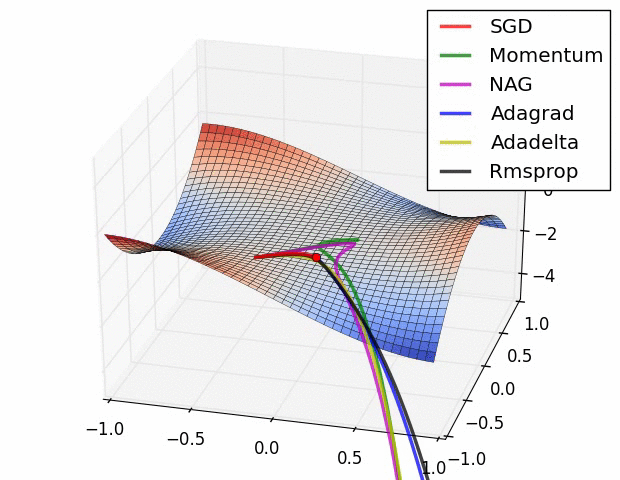
여러 가지 옵티마이저 중에서 어떤 것이 가장 좋다고 말하기는 어렵다.
문제마다, 데이터마다 달라지기 때문에 여러 옵티마이저를 적용하면서 서로 비교해보아야 한다.

수학으로 다시보는 역전파(Backpropagation Review with Math)

실습1 : Keras를 이용한 역전파 구현

케라스(keras)

신경망 모델을 간편하게 만들고 훈련시킬 수 있는 고수준 신경망 API
텐서의 조작, 미분 등의 low-level 연산을 만들지 않아도 잘 동작함
텐서플로우(Tensorflow)를 포함한 프레임워크와 함께 사용할 수 있으며 빠르고 간편한 프로토타이핑이 가능
신경망 구축시 가장 많이 사용되는 방법 : Sequential
신경망 학습 메커니즘
1. 학습 데이터 로드(Load data)
2. 모델 정의(Define model)
3. 컴파일(Compile)
4. 모델 학습(Fit)
5. 모델 검증(Evaluate)

### 1. 학습 데이터(선형 데이터) 만들기

def make_samples(n=1000):
    study = np.random.uniform(1, 8, (n, 1))
    sleep = np.random.uniform(1, 8, (n, 1))
    
    y = 5 * study + 2 * sleep + 40
    X = np.append(study, sleep, axis = 1)
    
    # 정규화 
    X = X / np.amax(X, axis = 0)
    y = y / 100
    
    return X, y



import numpy as np
import matplotlib.pyplot as plt
X, y = make_samples()
X[:10]

"""
array([[0.76155759, 0.4065224 ],
       [0.78699611, 0.19627527],
       [0.39267953, 0.53940436],
       [0.36391073, 0.99427628],
       [0.64412524, 0.48054391],
       [0.22616247, 0.13942684],
       [0.70853207, 0.3407582 ],
       [0.85016525, 0.44315516],
       [0.26123166, 0.63737043],
       [0.94228448, 0.48463672]])
"""




### 2. 필요한 라이브러리를 불러온 후 신경망을 구축하고 컴파일(compile)

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential()

# 신경망 모델 구조 정의
"""
Dense(A, input_dim=B, activation=C)
A : 출력 뉴런(노드) 수
B : 입력 뉴런(노드) 수(맨 처음 입력층에서만 사용)
C : activation 활성화 함수
"""
model.add(Dense(3, input_dim=2, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

# 컴파일 단계, 옵티마이저 & 손실함수 & 측정지표 연결해서 계산 그래프의 구성 마무리 
model.compile(optimizer='sgd', loss='mse', metrics=['mae', 'mse'])  # 회귀
# model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) ----> 분류인 경우 

results = model.fit(X,y, epochs=50)

results.history.keys()
"""
dict_keys(['loss', 'mae', 'mse'])
"""




### 3. 손실의 감소 시각화
plt.plot(results.history['loss'])

plt.plot(results.history['mae'])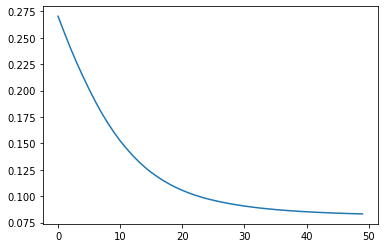

실습2 : Fashion MNIST 예제를 통한 신경망 구현(이미지 분류)

=> N412_Fashion MNIST 실습.ipynb

🧐 Review

신경망(Neural Network)에서 사용할 초기 가중치(파라미터,parameter) 임의로 설정
설정한 파라미터를 이용하여 입력 데이터를 신경망에 넣은 후 순전파 과정을 거쳐 출력값(Output)을 얻는다.
출력값과 타겟(Target, Label)을 비교하여 손실(Loss)를 계산합니다.
손실(Loss)의 Gradient를 계산하여 Gradient가 줄어드는 방향으로 가중치를 업데이트한다.
이 때 각 가중치의 Gradient를 계산할 수 있도록 손실 정보를 전달하는 과정을 역전파(Backpropagation)이라고 한다.
얼마만큼의 데이터를 사용하여 가중치를 어떻게 업데이트 할 지를 결정합니다.
이를 옵티마이저(Optimizer)라는 하이퍼파라미터로 정해줍니다. (Stochastic or Batch 등...)

References

다음으로는 경사하강법의 변형 중 한 방법인 뉴턴 메소드를 사용한 BFGS(Broyden–Fletcher–Goldfarb–Shanno) 방법을 적용한 신경망으로 학습을 진행해 보겠습니다. (코드 와 설명은 welch lab 에서 확인 가능합니다.)

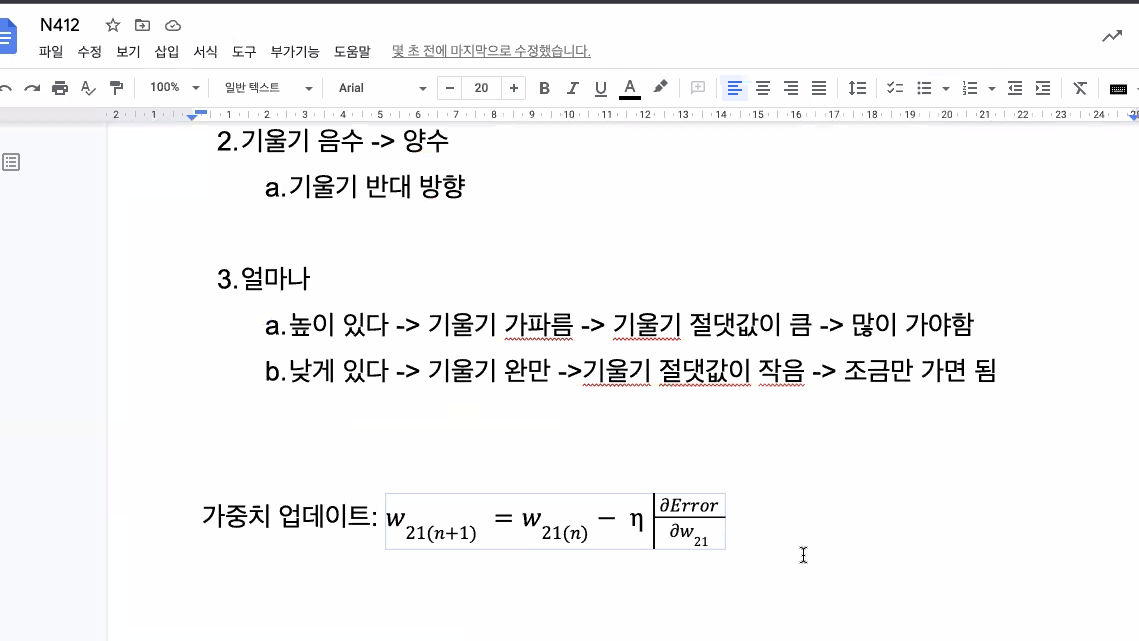
chain rule

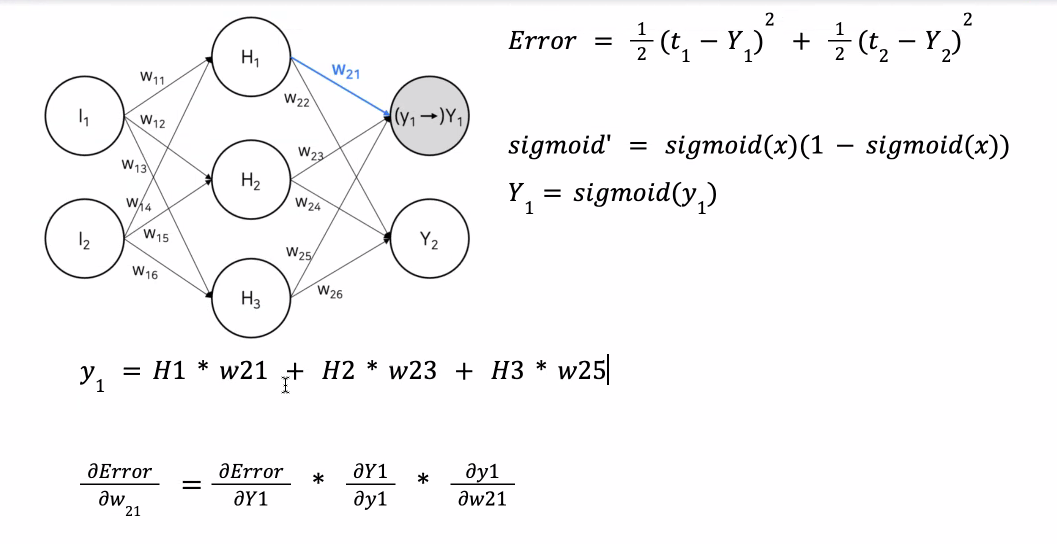
여기서 d는 편미분의 derivative를 의미.
dError/dw21 = (dError/Y1)(dY1/dy1)(dy1/dw21)

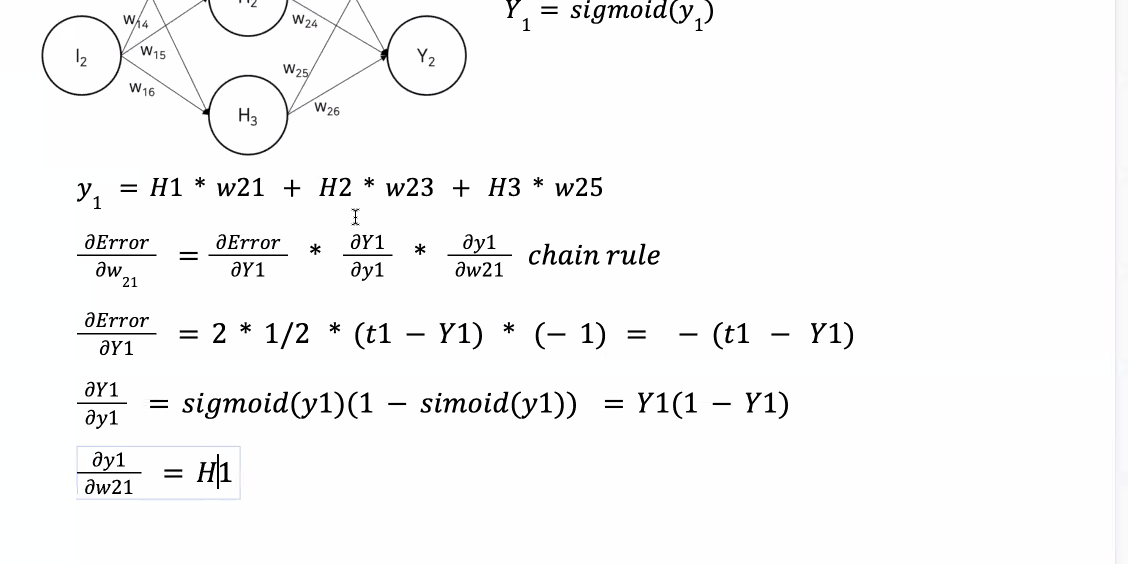
학습률 : 업데이트를 얼마나 조금?많이? 할 것인지 결정
가중치의 기울기를 chain rule을 이용해 구하는 전반적인 과정이 역전파 알고리즘
구한 기울기를 이용해 가중치를 반대 방향으로 업데이트하는 과정이 경사 하강법

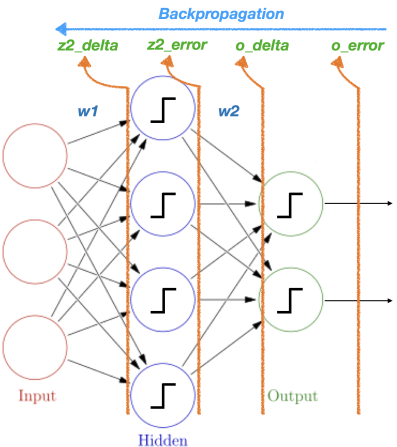
o_error 값이 Y
o_delta 값이 y
z2_error 값이 H
z2_delta 값이 h

코치님 혹시 코드문제 1번의 예제 1번만 설명해 주실 수 있을까요? (플러스 연산에 대한 역전파)
=> 곱셈 노드의 미분 / 덧셈 노드의 미분

code1 - 곱셈 노드 역전파
code2 - Z : 각 노드

Epoch2 = 학습 데이터셋 전체를 두 번 학습하는 것
Batch size = 한 번에 몇 개의 데이터를 학습할 것인가

iteration할 때마다 가중치 업데이트
관측치 = 100일 때 batch_size = 100이면 전체 데이터(100)을 모두 예측하고 실제값과 비교하여 가중치를 1회 업데이트.
관측치 = 100일 때 batch_size = 10이면 전체 데이터(100) 중 10개 데이터에 대해 예측하고 실제값과 비교 후, 가중치 업데이트가 10회 발생.

역전파, 가중치
chain rule
sequential, dense, input_dim
손실함수(loss function) : categorical_crossentropy, sparse_categorical_crossentropy, binary classification loss function
batch, epoch, iteration
SGD' (Stochastic Gradient Descent, 확률적 경사하강법)
이진 분류(일반적으로)
- 출력층 : 노드 수 1
- 활성화 함수 : sigmoid (>softmax를 사용한다면 값을 어떻게 변경? 왜 sigmoid 사용?)
- 손실함수 : binary_crossentropy
input/hidden/output layer, 가중치(weight), 편향(bias), parameter
학습률( $\eta$ ) : 학습할 정도를 정해 주는 parameter(역전파 과정에서 신경망의 가중치를 갱신할 수치가 계산되지만, 항상 그 값의 100%를 반영하는 것은 아니다.)