🏆 학습목표

• 케라스를 이용하여 모델 구조를 구축해보고 각 함수(메서드)의 의미를 이해한다.
• 과적합(Overfitting) 방지를 위한 가중치 Regularization의 방법을 알아보고 각 방법의 정의와 특징을 설명할 수 있습니다.
• 다양한 활성화 함수(Activation function)를 알아보고 특정 활성화 함수가 어떤 경우에 사용 되는지 설명할 수 있습니다.

---

Keras : 간단한 신경망 구현

실습 colab

손실 함수(Cost function) 혹은 오차 함수(Error function)

손실함수는 문제의 종류(이진 분류, 다중 분류, 회귀)에 따라 잘 선택해주어야 한다.
그 종류로는 다음의 2가지가 있다.

평균 제곱 기반

1. MSE(Mean Squared Error)

   $\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$

2. RMSE(Root Mean Squared Error)

   $\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}}$

3. MAE(Mean Absolute Error)

   $\frac{1}{n}\sum_{i=1}^{n}\left \vert y_{i} - \hat{y_{i}} \right \vert$

4. 이 외에도 R-Squared 등의 오차 함수를 사용한다.

엔트로피 기반

1. BCE(Binary Crossentropy)

   $-\sum_{c=1}^{C} q(y_c) log(q(y_c)), \quad q(y_c) \in (1, -1)$

2. CCE(Categorical Crossentropy)

   $-\sum_{c=1}^{C} q(y_c)log(q(y_c))$

※ 케라스에서 제공하는 여러 가지 손실 함수

과적합 방지 방법(Regularization Strategies)

신경망(Neural Network)은 매개 변수가 상당히 많은 복잡한 모델로 훈련 데이터에 쉽게 과적합(Overfit)되는 경향이 있다.

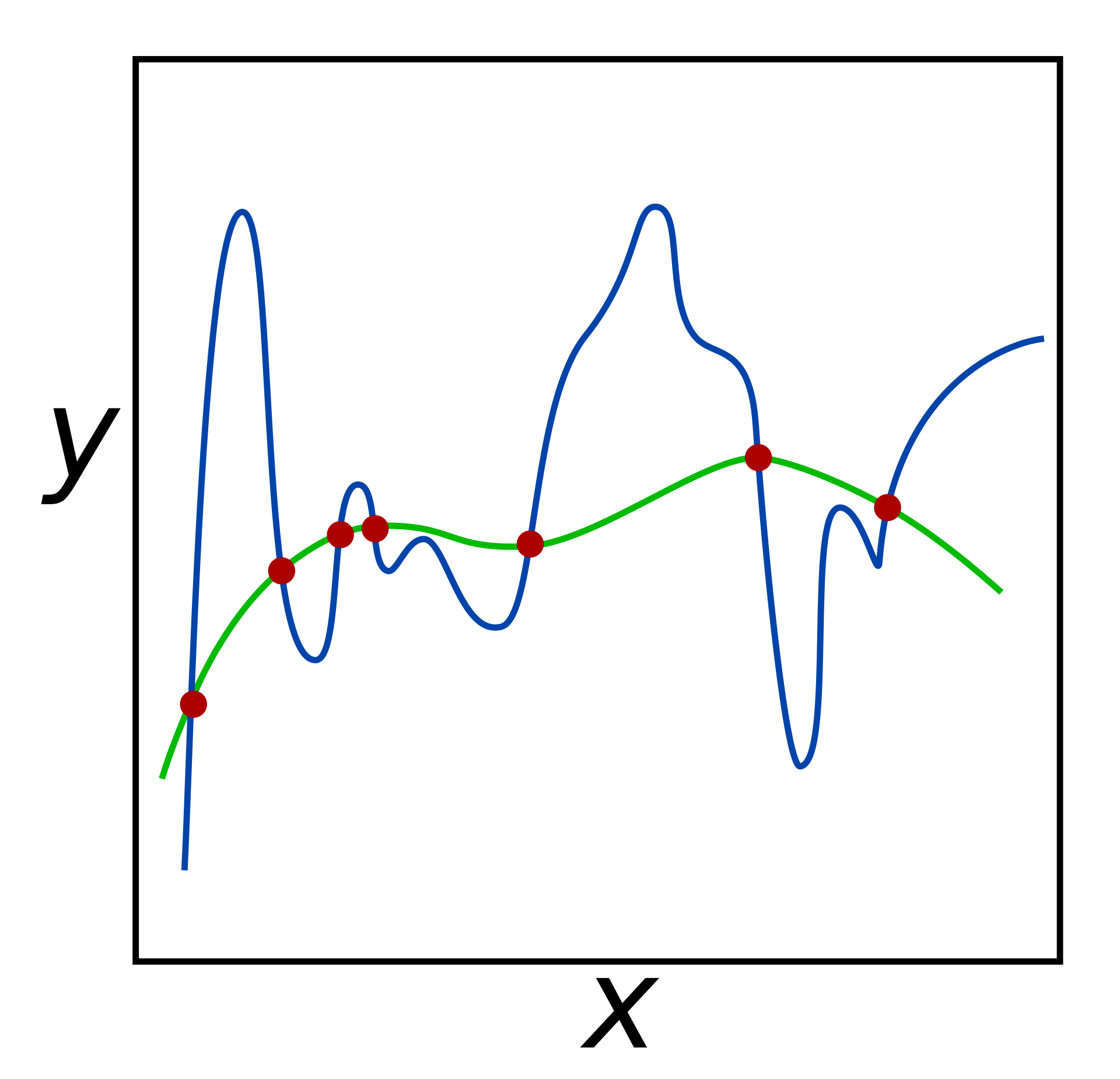
일반적인 Regularization 방법들

1. 조기 종료(Early Stopping)

학습(Train) 데이터에 대한 손실은 계속 줄어들지만 검증(Validation) 데이터셋에 대한 손실은 증가한다면 학습을 종료하도록 설정하는 방법

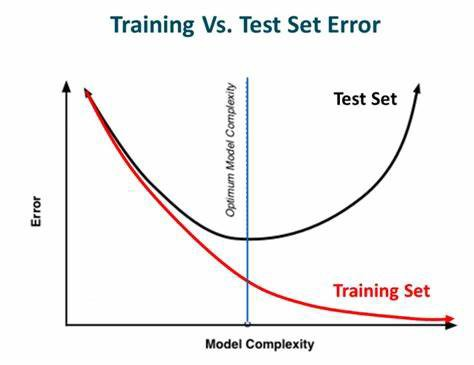
2. 가중치 감소(Weight Decay)

과적합은 가중치의 값이 클 때 주로 발생하여
가중치 감소에서는 손실 함수(Cost function)에 가중치와 관련된 항을 추가하여 값이 너무 커지지 않도록 조정한다.
여기서 가중치 항을 어떻게 추가할지에 따라 L1 Regularization, L2 Regularization 으로 나뉜다.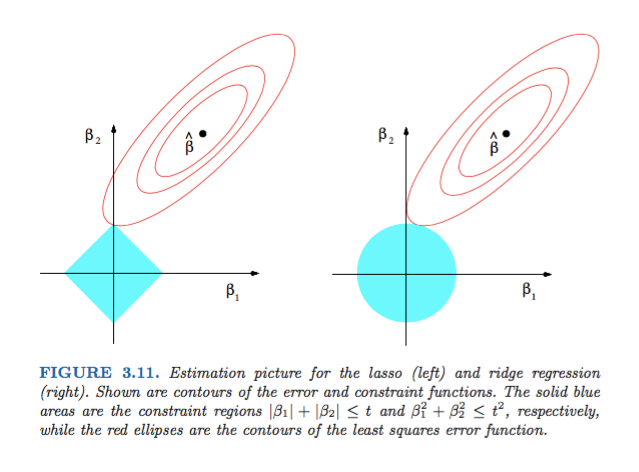

• 가중치 : $\beta_1$, $\beta_2$

• $\lambda$ : (가중치에 대한 )패널티(규제)를 조정하는 계수

  • $\lambda$ 크면, 패널티 크게
  • $\lambda$ 작으면, 패널티 작게

• 빨간 원 크기 = cost function 크기

• 파란색 마름모 & 원 = 규제

  • 파란색 증가 -> 규제 감소
  • 파란색 감소 -> 규제 증가

3. 가중치 제한(Weight Constraint)

가중치 감소와 유사한 목적을 달성하기 위해서 특정 가중치를 제거하거나 범위를 제한하는 방법
유사한 방법으로 Weight Decusion and Weight Restriction 이 있다.

4. 드롭아웃(Dropout)

Dropout은 iteration 마다 레이어 노드 중 일부를 사용하지 않으면서 학습을 진행하는 방법으로
매 번 다른 노드가 학습되면서 전체 가중치가 과적합되는 것을 방지할 수 있다.

Keras : Regularization 적용

조기 종료(Early Stopping)

• tf.keras.callbacks.EarlyStopping

실습 colab

가중치 감소(Weight Decay)

가중치 감소 방식에서는 손실 함수에 가중치와 관련된 항을 추가하여 손실 함수를 최적화하는 과정에서 가중치가 너무 커지지 않도록 조정한다.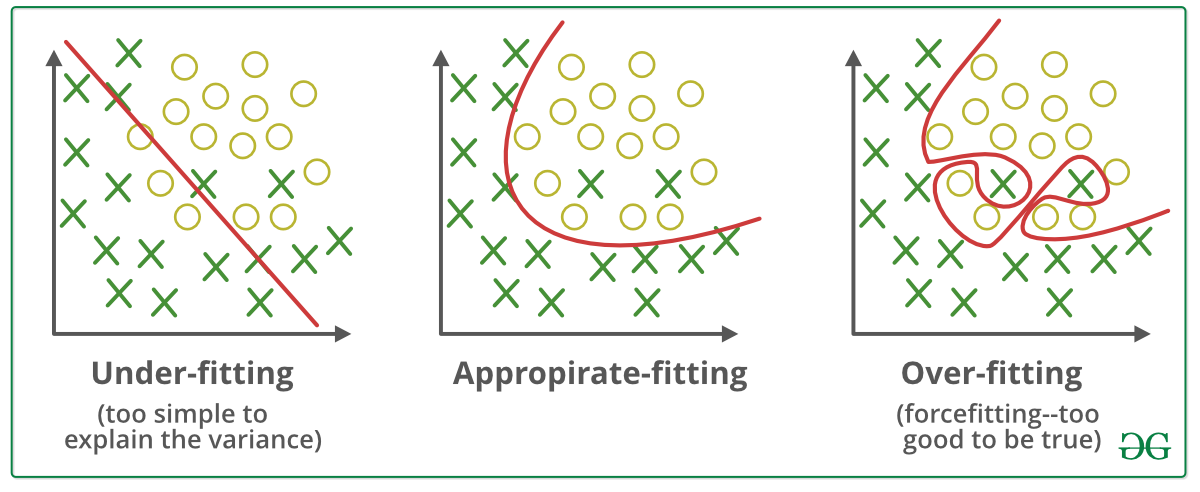위 그림에서 과적합(Over-fitting)을 나타낼 때 구불구불한 경계면이 형성되는 것을 확인할 수 있으며 이렇게 굽이치는 그래프가 형성될 때 가중치는 커지기 마련이다.

가중치 감소는 애초부터 가중치가 큰 값을 갖지 못하게하여(손실 함수에 가중치와 관련된 항 추가) 과적합이 나타나지 않도록 만든다.

L1 Regularization(Lasso)

• 값이 아주 작은 것들 -> 0
• 규제가 커지면 0이되는 것들이 많아짐

L2 Regularization(Lidge)

• 값이 작은 것들 -> 아예 0이 되지는 않음
• 규제가 커지면 아예 0이 되지는 않고, 큰 것들부터 줄임

---

*loss function의 파라미터 크기 반영

*$\theta_w$ : 가중치들의 집합

*lambda = 규제 (비례관계)

실습 colab

가중치 제한(Weight Constraints)

• 가중치의 범위를 수동으로(직접) 제한하는 방법
• 케라스의 여러 가지 가중치 제한 방법
  
  

실습 colab

드롭아웃(Dropout)

• 지정해 준 비율(켜는 노드의 비율)만큼 모델 내에 있는 특정 레이어의 노드 연결을 강제로 끊어주는 방식
  노드를 끈다 = input값 0 => 노드를 끈 것과 같은 효과
• 매 Iteration 마다 랜덤하게 노드를 차단하여 다른 가중치를 학습하도록 조정하기 때문에 과적합을 방지할 수 있다.
• 학습할 때만 노드를 끄는 것

실습 colab

조금 더 나은 모델학습을 위하여!

학습률 감소(Learning rate decay)

• 옵티마이저(Optimizer)의 다양한 하이퍼파라미터를 조정하여 적용

tf.keras.optimizers.Adam(
  learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False,
  name='Adam'
)

• 신경망을 컴파일 하는 코드에 하이퍼파라미터를 조정한 옵티마이저를 적용한다.

model.compile(optimizer=tf.keras.optimizers.Adam(lr=0.001, beta_1 = 0.89)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])

학습률 계획(Learning rate scheduling)

• 학습 과정에 학습률을 바꿔가는 메카니즘을 골라서 처리하는 과정

• https://throwexception.tistory.com/1189
  

• 학습률 계획(Learning rate scheduling)은 아래와 같이 학습률에 대한 다양한 파라미터를 지정한 뒤에 옵티마이저(Optimizer)의 학습률에 이를 적용할 수 있다.

### ex1
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(
  initial_learning_rate=1e-2,
  decay_steps=10000,
  decay_rate=0.9)

optimizer = tf.keras.optimizers.SGD(learning_rate=lr_schedule)



### ex2
lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate=1e-2,
    decay_steps=10000,
    decay_rate=0.9)
    
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_schedule)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])
             
             

### ex3 : 학습률 계획 커스터마이징
def decayed_learning_rate(step):
  step = min(step, decay_steps)
  cosine_decay = 0.5 * (1 + cos(pi * step / decay_steps))
  decayed = (1 - alpha) * cosine_decay + alpha  # -1 < cosine value < 1
  return initial_learning_rate * decayed

• 코사인 학습률 감쇄 스케줄

  • 특정 반복 회차, 에폭에서 감쇄하는게 아니라 시간에 대한 함수를 사용하는데, 학습률은 모든 에폭 회차에 대한 함수로 정해짐

  • 초기 학습률과 에폭 수만 필요하지, 이전에 봤던 다른 하이퍼 파라미터가 필요하지 않다. 그래서 코사인 스캐줄러는 이전에 본 스탭 감쇄 스캐줄러보다 다루기가 쉬우며, 일반적으로 학습을 길게 할수록 잘 동작하는 경향을 보인다.

    => 초기 학습률과 모델이 얼마나 오래 학습시킬지만 튜닝하면 됨

first_decay_steps = 1000
initial_learning_rate = 0.01
lr_decayed_fn = (
  tf.keras.experimental.CosineDecayRestarts(    
      initial_learning_rate,
      first_decay_steps))
      
      
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_decayed_fn)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])

• 다양한 신경망 학습 스킬이 소개되어 있는 논문
  Bag of Tricks for Image Classification with Convolutional Neural Networks

활성화 함수(Activation Functions)

tanh (Hyperbolic Tangent)

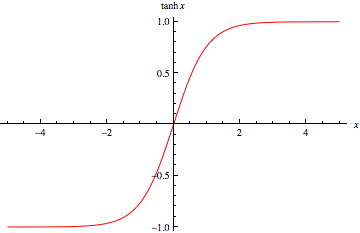
• 시그모이드 함수를 변형한 함수로
  0 부근에서 시그모이드 함수보다 더 가파르기 때문에 더 빠르게 최저점에 수렴할 수 있다
  
  $\begin{aligned} \text{sigmoid :} &\frac{1}{1+e^{-x}} \\ \tanh : &\frac{1-e^{-x}}{1+e^{-x}} = \frac{2}{1+e^{-2x}} - 1 = 2 \text{sigmoid}(2x) - 1 \end{aligned}$

Leaky ReLU

• ReLU를 개선한 함수
• ReLU 함수는 0보다 작은 값이 입력될 때에는 어떤 값이 입력 되든지 0의 값을 반환하지만
  Leaky ReLU는 음수 부분에도 기울기를 넣어 입력값이 음수인 경우도 살려준다.
• 일반적으로 Leaky ReLU 의 음수 부분은 0.01 의 기울기를 갖는다.
• Parametric ReLU 처럼 기울기를 하이퍼 파라미터로 정해줄 수도 있다.

Softmax

• 시그모이드 함수를 다중 분류에 사용할 수 있도록 변형한 활성화 함수
• 각 클래스에 대한 가중합 값을 소프트맥스에 통과시키면 모든 클래스의 값의 합이 1이 되는 확률값으로 변환된다.
  

---

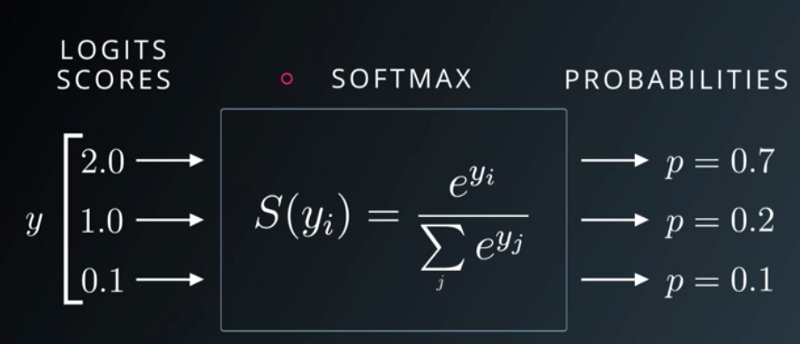
🧐 Review

• 손글씨 MNIST, Fashion MNIST와 같은 예제를 Keras를 사용하여 스스로의 힘으로 풀 수 있는지 확인
  ( 모든 코드를 외워야 할 필요는 없지만
  학습 메커니즘 흐름과 포인트(출력층 노드 수, 출력층 활성화 함수, 손실 함수 설정)는 숙지할 것! )

• 신경망의 과적합을 막기 위해 적용할 수 있는 Regularization 방법에 대한 대략적인 개념

  • 콜백(Callback)을 이용한 학습 조기 종료(Early Stopping)
  • 가중치 감소(Weight Decay)
  • 가중치 제한(Weight constriants)
  • 드롭아웃(Dropout)
  • 학습률 감소(Learning rate decay)와 학습률 계획(Learning rate scheduling)

• 새롭게 배운 활성화 함수와 각 함수의 특징

  • Hyperbolic Tangent (tanh) : 시그모이드(Sigmoid)와의 차이점
  • Leaky ReLU : 일반 ReLU 와의 차이점
  • 소프트맥스(Softmax) : 언제 사용하며 어떤 특징을 가지고 있는지

---

📚 reference

딥러닝 과정 맛보기