퍼셉트론

• 퍼셉트론은 입출력을 갖춘 알고리즘으로 입력을 주면 정해진 규칙에 따른 값을 출력한다.

• 퍼셉트론에서는 '가중치'와 '편향'을 매개변수로 설정한다.

• 퍼셉트론으로 AND, OR 게이트 등의 논리 회로를 표현할 수 있다.

• XOR 게이트는 단층 퍼셉트론으로는 표현할 수 있다.

• 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.

• 단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.

• 다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.

신경망

• 신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습할 수 있다. 즉 데이터를 보고 학습할 수 있는 것이다.

• 신경망 = 입력층 + 은닉층 + 출력층

• 활성화 함수 : 입력 신호의 총합을 출력 신호로 변환하는 함수

  • 계단 함수(단순 퍼셉트론)
  • 시그모이드 함수(다층 퍼셉트론, 신경망)
  • ReLU 함수
  • 층을 깊게 하는 의미 때문에 신경망에서는 활성화 함수로 비선형 함수 사용

• 넘파이의 다차원 배열을 잘 사용하면 신경망을 효율적으로 구현할 수 있다.

  • 배열 차원 수 = np.ndim(), 배열 형상 = .shape
  • 행렬의 내적 : 행렬의 형상 주의 (np.dot())

• 출력층의 활성화함수는 풀고자 하는 문제의 성질에 맞게 정함

  • 분류 : 출력층 노드 수=분류하고 싶은 클래스 수
    • 이진분류 : sigmoid, 노드 1개
    • 다중분류 : softmax(확률 출력), 노드 label수
      *신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식하므로 소프트맥스 함수를 적용해도 가장 큰 뉴런의 위치는 달라지지 않는다. 따라서 신경망으로 문류할 경우, 출력층의 소프트맥스 함수를 생략해도 되고 그것이 일반적이다.
  • 회귀 : 항등함수(입력=출력), 노드 1개

• MNIST 데이터셋

  • flatten : 1차원 넘파이 배열 / reshape : 넘파이 배열의 형상 바꿈
  • pickle : 실행 당시의 특정 객체 파일 저장 기능
  • np.dot, sigmoid : 신경망 구축
  • batch : 입력 데이터를 묶은 것으로 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있음, 묶음(이미지가 지폐처럼 다발로 묶인 것)

    배치처리는 컴퓨터로 계산할 때 이미지 1장당 처리 시간을 대폭 줄여줘 큰 이점을 준다.

    1. 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 고도로 최적화되어 있기 때문
    2. 커다란 신경망에서는 데이터 전송이 병목이 되는 경우가 자주 있다. -> 배치 처리를 함으로써 버스에 주는 부하를 줄임(느린 I/O를 통해 데이터를 읽는 횟수에 비해, 빠른 CPU나 GPU로 순수 계산을 수행하는 비율이 높아진다)
       
       즉, 배치 처리를 수행함으로써 큰 배열이 이뤄진 계산을 하게 되는데, 컴퓨터에서는 큰 배열을 한꺼번에 계산하는 것이 분할된 작은 배열을 여러 번 계산하는 것보다 빠르다.

신경망 학습

• 학습 : 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것

• 딥러닝 = 종단간 기계학습(end-to-end machine learning)

  • 데이터(입력)에서 목표한 결과(출력)를 사람의 개입 없이 얻는다는 의미
  • 신경망은 모든 문제를 주어진 데이터 그대로를 입력 데이터로 활용해 'end-to-end'로 학습할 수 있다.

• 훈련 데이터와 시험데이터를 나누는 이유

  • 범용 능력(아직 보지 못한 데이터(훈련 데이터에 포함되지 않는 데이터)로도 문제를 올바르게 풀어내는 능력)을 제대로 평가하기 위해
  • 오버피팅(overfitting; 한 데이터셋에만 지나치게 최적화된 상태)을 파하기 위해

• 손실함수(loss function)

  • 신경망이 최적의 매개변수 값을 탐색할때 기준이 되는 지표
  • 신경망 성능의 '나쁨'을 나타내는 지표 -> 현재의 신경망이 훈련 데이터를 얼마나 잘 처리하지 '못'하느냐를 나타냄
  • 일반적으로 평균 제곱 오차와 교차 엔트로피 오차를 사용한다.

    평균 제곱 오차(Mean Squared Error, MSE)
    
    $E = {1\over 2}\displaystyle\sum_{k}(y_k-t_k)^2$
    $y_k$ : 신경망의 출력(신경망이 추정한 값)
    $t_k$ : 정답 레이블 (정답에 해당하는 인덱스의 원소만 1이고 나머지는 0 ->원핫인코딩)
    $k$ : 데이터의 차원 수
    

    def mean_squared_error(y, t):
    	return 0.5 * np.sum((y-t)**2)

    # 정답레이블 / 정답 = '2'
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

    # 신경망 출력1 : '2'일 확률이 가장 높다고 추정함
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    mean_squared_error(np.array(y), np.array(t))
    >>> 0.097500000000000031

    # 신경망 출력2 : '7'일 확률이 가장 높다고 추정함
    y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    mean_squared_error(np.array(y), np.array(t))
    >>> 0.59750000000000003

    => 신경망 출력1의 손실 함수 출력이 더 작다 = 정답 레이블과의 오차가 작다
    => 정답에 가까움
    
    
    
    교차 엔트로피 오차(cross entropy error, CEE)
    
    $E = -\displaystyle\sum_{k}t_klogy_k$
    $log$ : 자연로그 $log_e$
    $y_k$ : 신경망의 출력
    $t_k$ : 정답 레이블 (정답에 해당하는 인덱스의 원소만 1이고 나머지는 0 ->원핫인코딩)
    ex) 신경망 출력 0.6 : $-log0.6 = 0.51$ / 신경망 출력 0.1 : $-log0.1 = 2.30$
    $x=1$ -> $y=0$
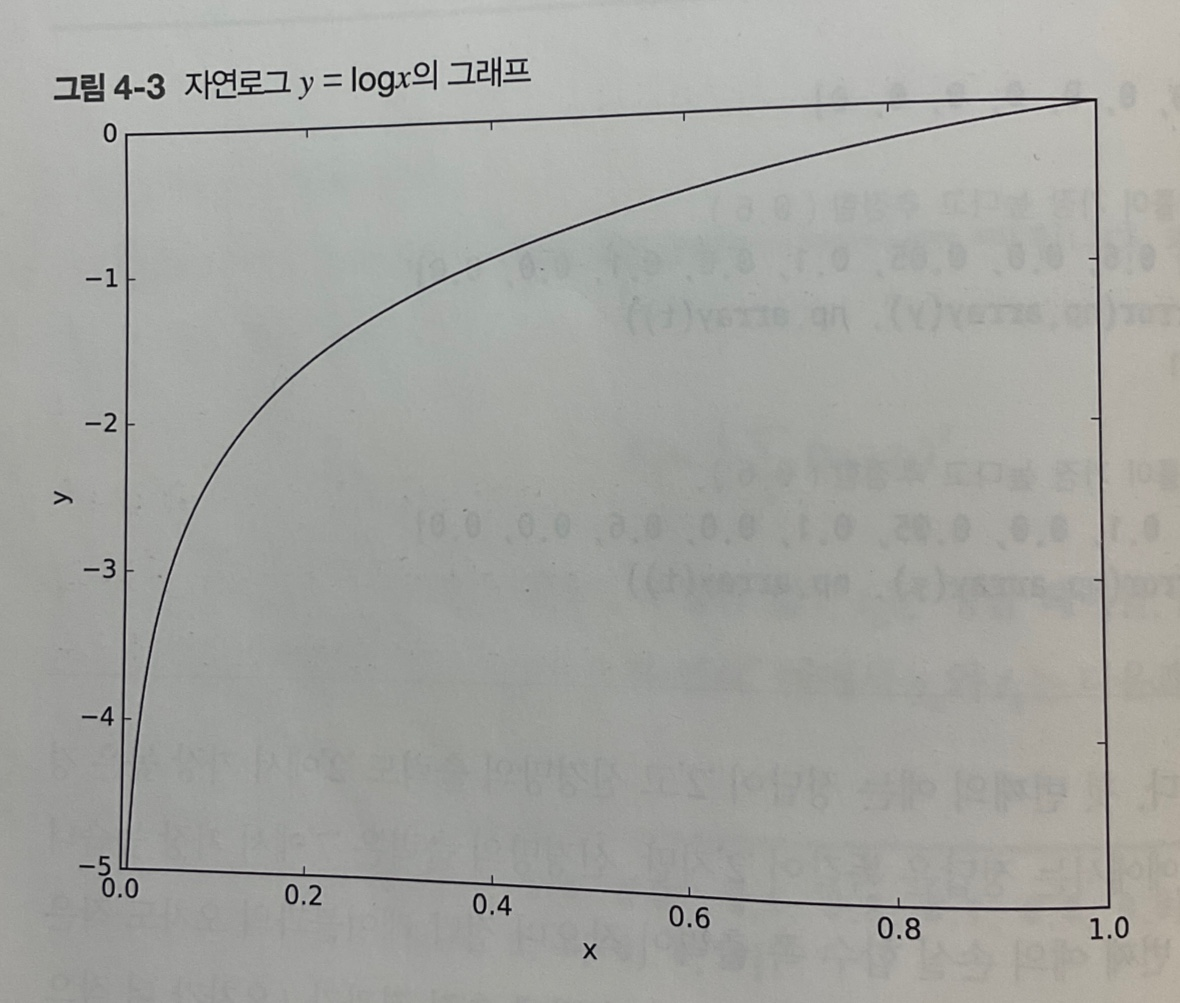    정답에 해당하는 출력($softmax$함수의 출력 = 특정 클래스가 정답일 확률)이 커질수록 $0$에 다가가다가, 그 출력이 $1$(정답)일 때 $0$(오차)이 됨

    def cross_entropy_error(y, t):
        delta = 1e-7
        return -np.sum(t*np.log(y+delta))
     # delta : 아주 작은 값을 더해 절대 0이 되지 않도록, 즉 마이너스 무한대가 발생하지 않도록 함 

    # 정답레이블 / 정답 = '2'
    t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

    # 신경망 출력1 : '2'일 확률이 가장 높다고 추정함
    y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
    cross_entropy_error(np.array(y), np.array(t))
    >>> 0.51082545709933802

    # 신경망 출력2 : '7'일 확률이 가장 높다고 추정함
    y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
    cross_entropy_error(np.array(y), np.array(t))
    >>> 2.3025840929945458

    => 결과(오차 값)가 더 작은 첫 번째 추정이 정답일 가능성이 높다
    
    
    로그란 무엇인가, 왜 통계에서 로그를 사용하는가? (회귀분석시 자연로그 해석)
    데이터 분석 시 식에 로그를 취하는 이유
    자연상수 e의 의미
    자연로그 계산기: 자연 상수 e의 의미와 자연로그의 의미

• 미니배치 학습

  평균 손실 함수
  
  $E = -{1\over N}\displaystyle\sum_{k}\displaystyle\sum_{t}t_{nk}logy_{nk}$
  $N$ : 데이터 개수
  $t_{nk}$ : n번째 데이터의 k번째 값, 정답 레이블
  $y_{nk}$ : 신경망의 출력

  미니배치(mini-batch) : 전체의 '근사치'로 이용하기 위한 신경망 학습에서의 훈련 데이터 일부
  미니배치 학습 : 전체 훈련 데이터 중 일부를 무작위로 일부를 뽑아 학습하는 방법으로 np.random.choice()를 이용한다.

• 신경망 학습에서는 최적의 매개변수(가중치와 편향)를 탐색할 때 손실 함수의 값을 가능한 한 작게 하는 매개변수 값을 찾는다. 이때 매개변수의 미분(정확히는 기울기)을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다.

• 가중치 매개변수의 손실함수의 미분 = 가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하나

  • 미분값 (-) -> 가중치 매개변수 (+) 방향으로 변화
  • 미분값 (+) -> 가중치 매개변수 (-) 방향으로 변화
  • 미분값 0 -> 어느 쪽으로 움직여도 손실 함수의 값은 달라지지 않아 갱신이 멈춤

• 신경망을 학습할 때 정확도는 매개변수의 미분이 대부분의 장소에서 0이 되므로 지표로 삼아선 안된다.

미분

• '특정 순간'의 변화량
  ex) 10분에서 2km씩 달렸을 때, 10분이라는 시간을 가능한 한 줄여(직전 1분에 달린 거리, 직전 1초에 달린 거리, 직전 0.1초에 달린 거리, ...식으로 갈수록 간격을 줄여) 한 순간의 변화량(어느 순간의 속도)을 얻는 것
  
  
• ${df(x)\over dx} = \displaystyle\lim_{h \to 0}{f(x+h)-f(x)\over h}$
  => $x$의 '작은 변화'가 함수 $f(x)$를 얼마나 변화시키느냐를 의미 ($h$=시간)
  
  
• 수치 미분 : 아주 작은 차분(임의 두 점에서의 함수 값들의 차이)으로 미분하는 것

  ### 수치 미분
  def numerical_diff(f, x):
     h = 1e-4  #0.0001
     return (f(x+h) - f(x-h)) / (2*h) 

  편미분
  변수가 여럿인 함수에 대한 미분으로 여러 변수 중 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정한다.

• 경사법(경사하강법)
  : 기울기를 이용해 손실 함수의 최솟값(또는 가능한 한 작은 값)을 찾으려는 것
  $x_i = x_i-\eta{\delta{f}\over\delta{X_i}}$

  • $\eta$ = 학습률(learning rate)
    : 한 번의 학습으로 얼마만큼 학습해야 할지, 즉 매개변수 값을 얼마나 갱신하느냐를 정하는 것(너무 크면 큰 값으로 발산하고 너무 작으면 거의 갱신되지 않은 채 끝난다)

    하이퍼파라미터
    훈련 데이터와 학습 알고리즘에 의해서 '자동'으로 획득되는 가중치와 편향 같은 신경망의 매개변수와는 달리 학습률 같이 사람이 직접 설정해야 하는 매개변수. 일반적으로는 이들 하이퍼파라미터는 여러 후보 값 중에서 시험을 통해 가장 잘 학습하는 값을 찾는 과정을 거쳐야 한다.

• 신경망에서의 기울기
  
  $W = \left(\begin{array}{rrr} w_{11}&w_{21}&w_{31}\\ w_{12}&w_{22}&w_{32} \end{array}\right)$ ${\delta{L}\over \delta{W}} = \left(\begin{array}{rrr} {\delta{L}\over \delta{w_{11}}}&{\delta{L}\over \delta{w_{21}}}&{\delta{L}\over \delta{w_{31}}}\\ {\delta{L}\over \delta{w_{12}}}&{\delta{L}\over \delta{w_{22}}}&{\delta{L}\over \delta{w_{32}}} \end{array}\right)$
  
  
  $W$ = 가중치
  $L$ = 손실 함수
  ${\delta{L}\over \delta{W}}$ = 각각의 원소에 관한 편미분, 경사
  ${\delta{L}\over \delta{w11}}$ = $w_{11}$을 조금 변경했을 때 손실 함수 $L$이 얼마나 변화하느냐

import sys, os
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient


class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3) # 정규분포로 초기화
	"""
        array([[ 1.35072279, -2.65960474, -2.47920647],
               [ 1.22166762,  0.00577551,  0.55534712]])
        """
    
    # 예측    
    def predict(self, x):
        return np.dot(x, self.W) # 행렬의 곱

	
    # 손실 함수
    def loss(self, x, t):  # x=입력 데이터, t=정답 레이블
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)

        return loss

x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])

net = simpleNet()

f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)

print(dW)

• 확률적 경사 하강법 절차
  • 확률적 경사 하강법(stochastic gradient descent, SGD)
    : '확률적으로 무작위로 골라낸 데이터'에 대해 수행하는 경사 하강법
  • 전제
    : 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 한다.
  • 1단계 - 미니배치
    : 훈련 데이터 중 일부를 무작위로 가져온다. 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실함수 값을 줄이는 것이 목표다.
  • 2단계 - 기울기 산출
    : 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다. 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시한다.
  • 3단계 - 매개변수 갱신
    : 가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
  • 4단계 - 반복
    : 1~3단계를 반복한다.