[알고리즘] 최소 신장 트리: Kruskal 알고리즘

안수진·2024년 5월 17일

Algorithm

목록 보기

14/22

🎄 신장 트리

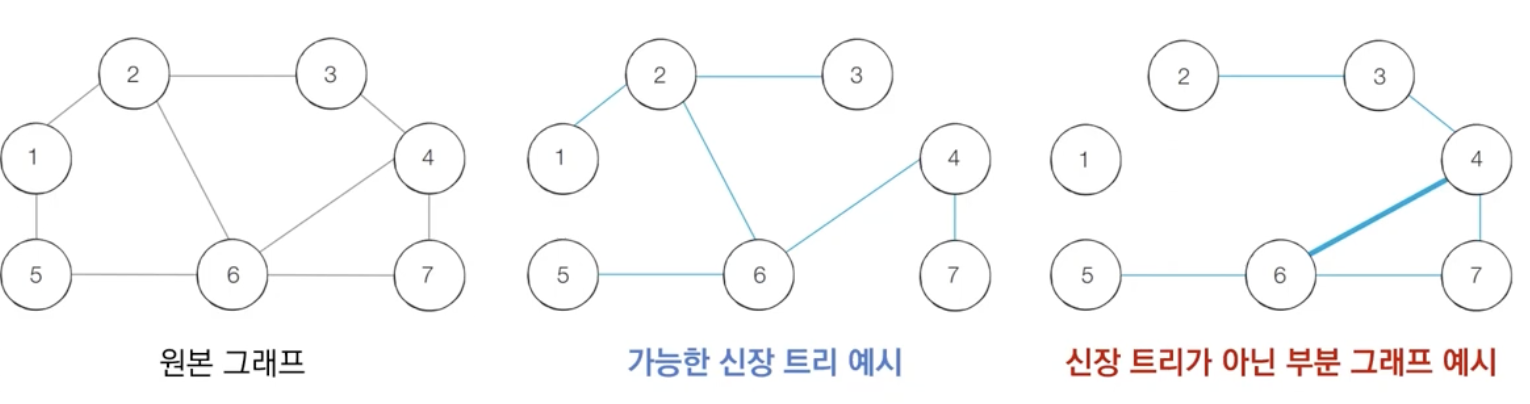
그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프

모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 조건이기도 하다.

🎄 최소 신장 트리

최소한의 비용으로 구성되는 신장 트리를 찾아야 할 때 어떻게 해야할까?

예를 들어 N개의 도시가 존재하는 상황에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있게 도로를 설치하는 경우를 생각해 보자.
두 도시 A, B를 선택했을 때 A에서 B로 이동하는 경로가 반드시 존재하도록 도로를 설치한다.

📌 크루스칼 알고리즘

대표적인 최소 신장 트리 알고리즘이며, 그리디 알고리즘으로 분류된다.

알고리즘 동작 과정

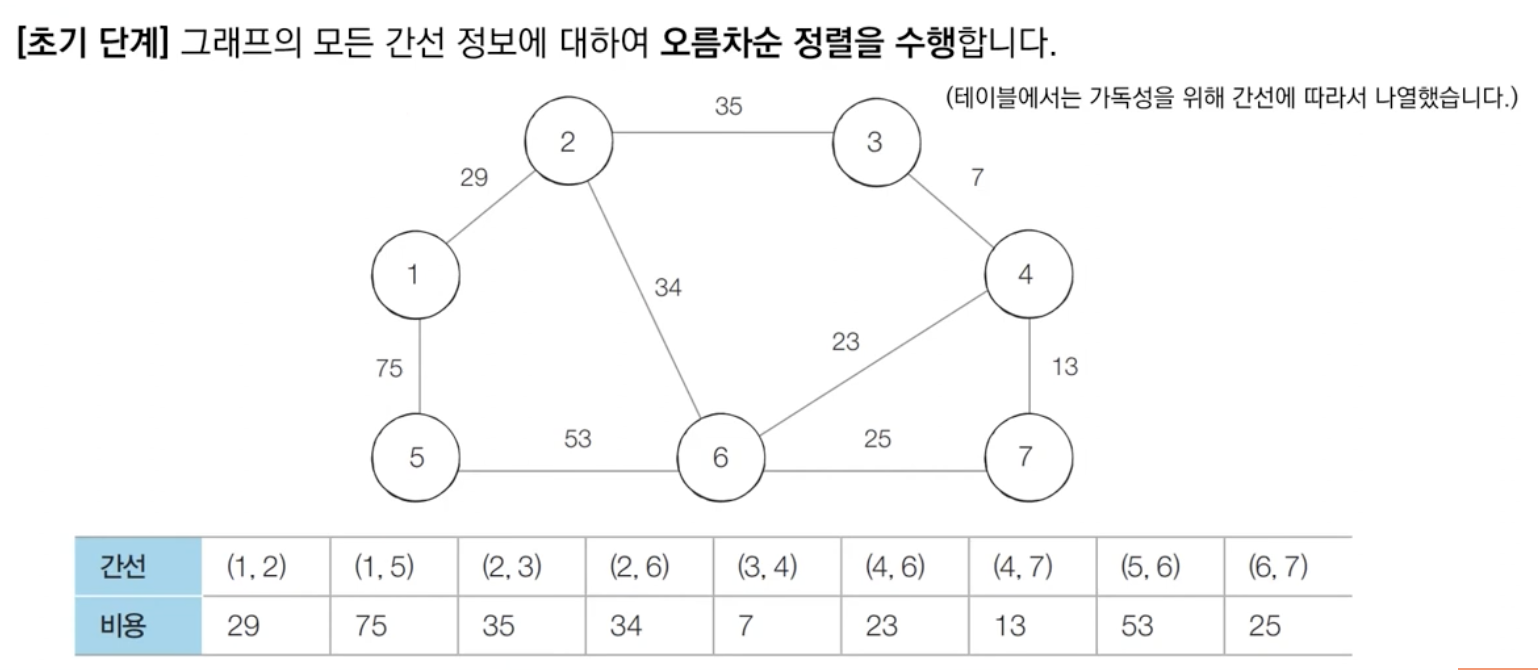
간선 데이터를 비용에 따라 오름차순으로 정렬합니다.
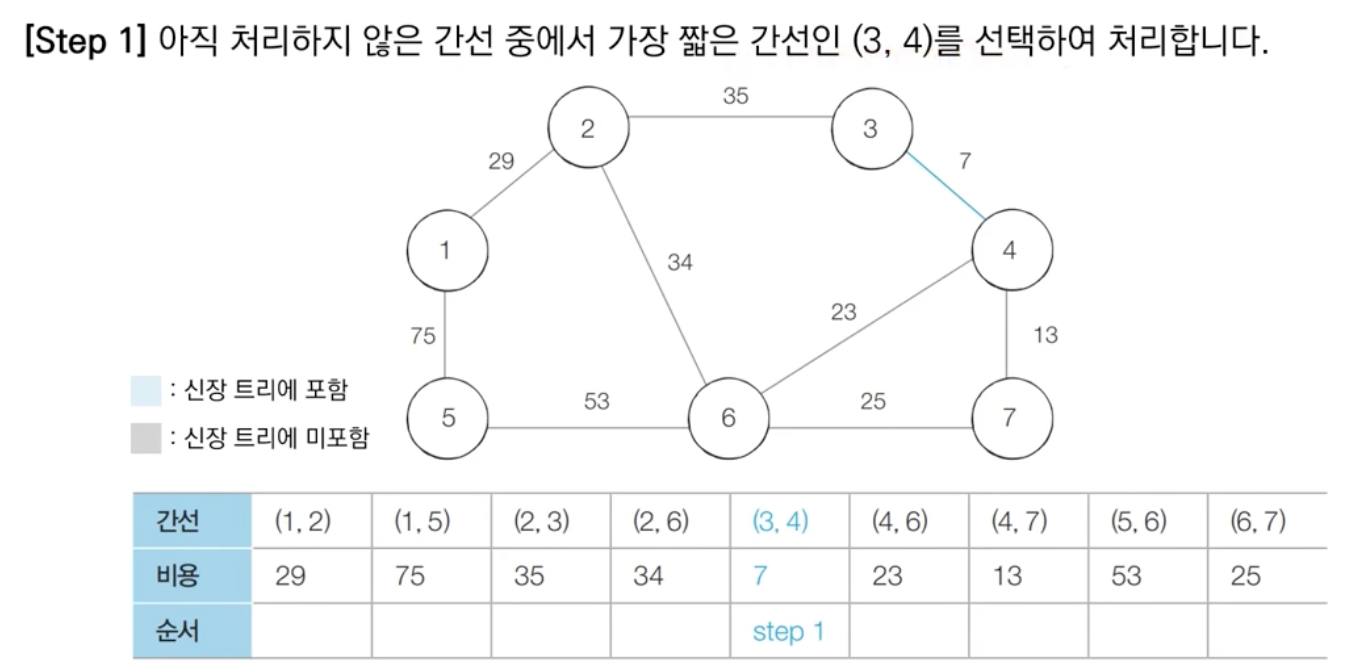
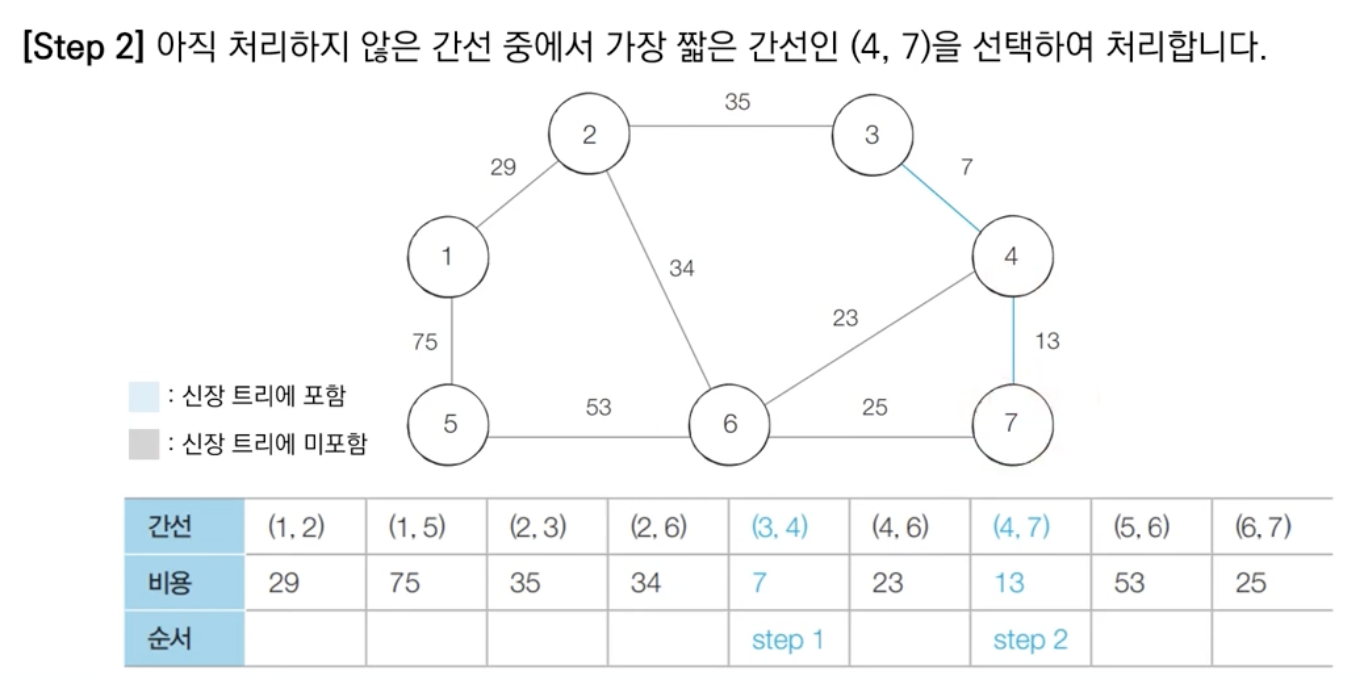
비용이 적은 간선부터 처리할 수 있도록
간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인합니다.
1) 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킵니다.
2) 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않습니다.
이 과정은 유니온 파인드 알고리즘을 이용한다.
모든 간선에 대하여 2번의 과정을 반복합니다.

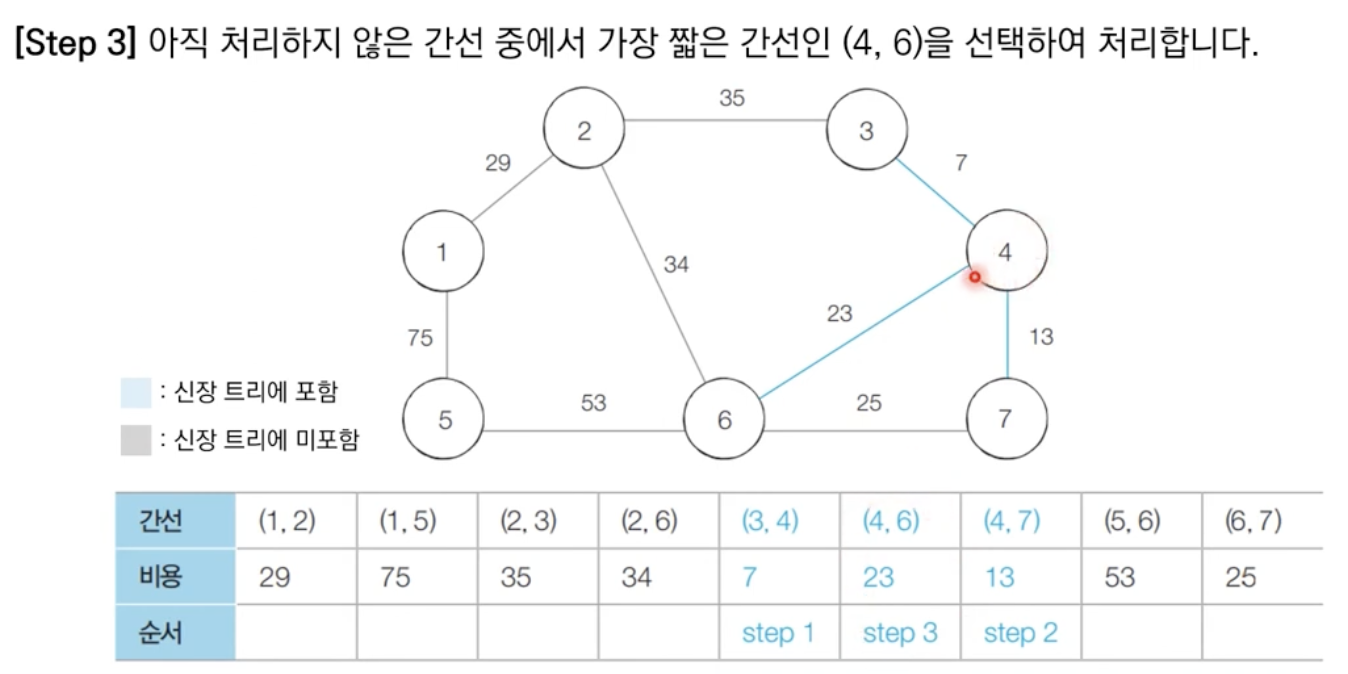
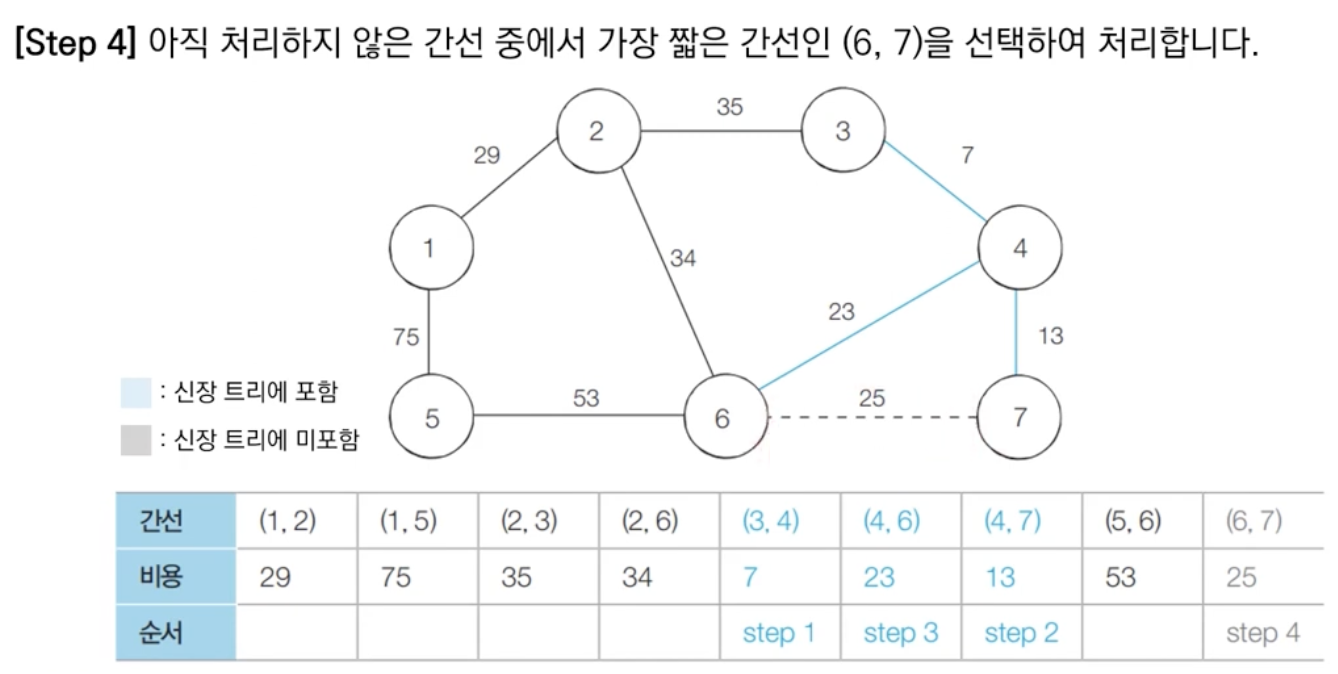
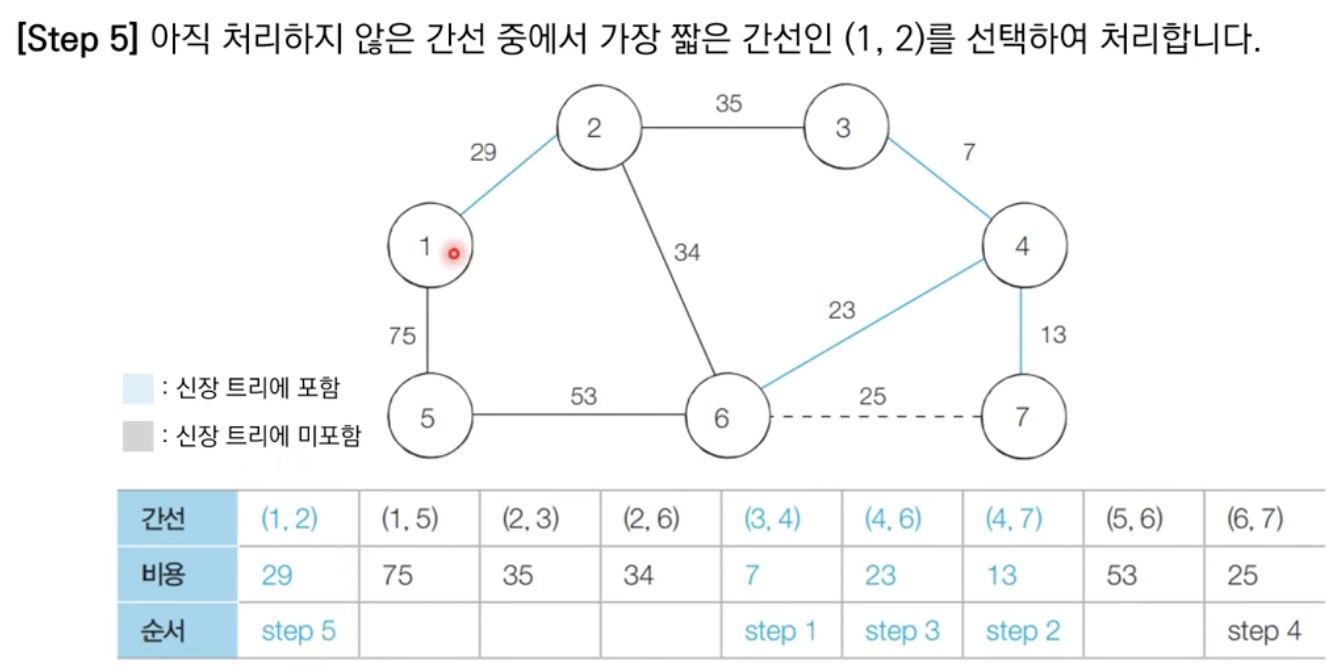
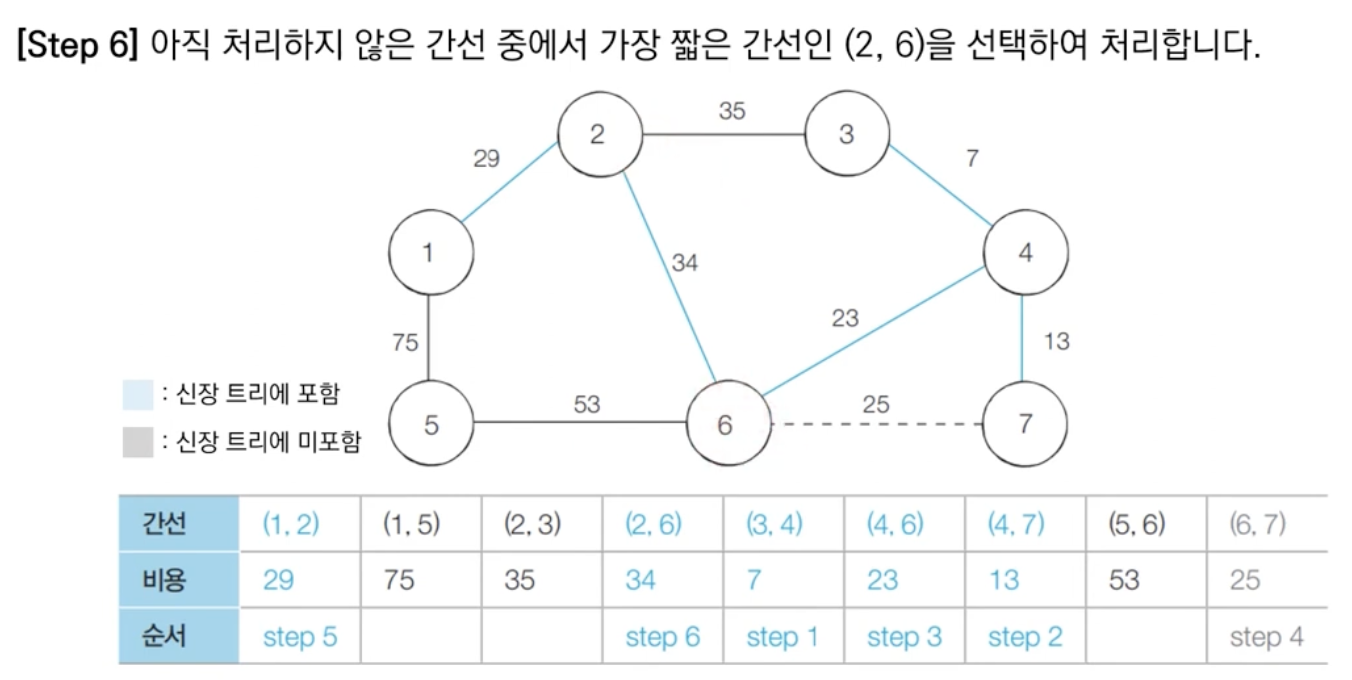
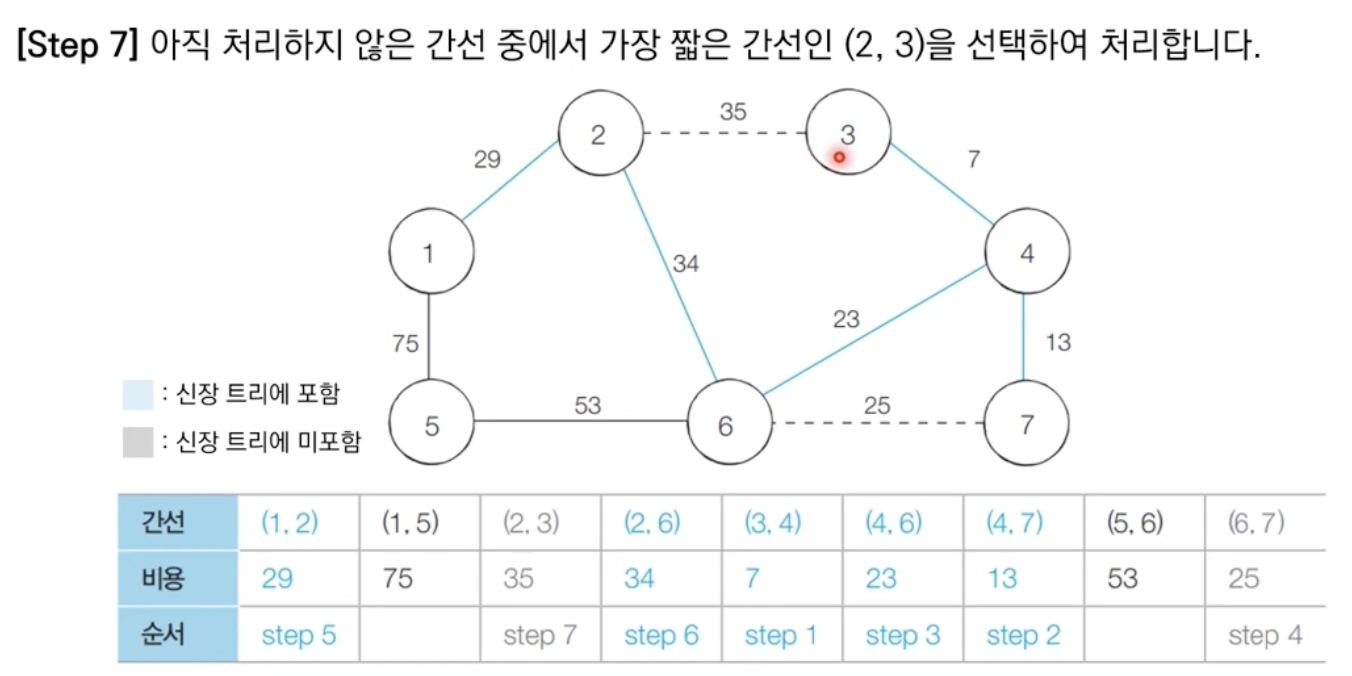
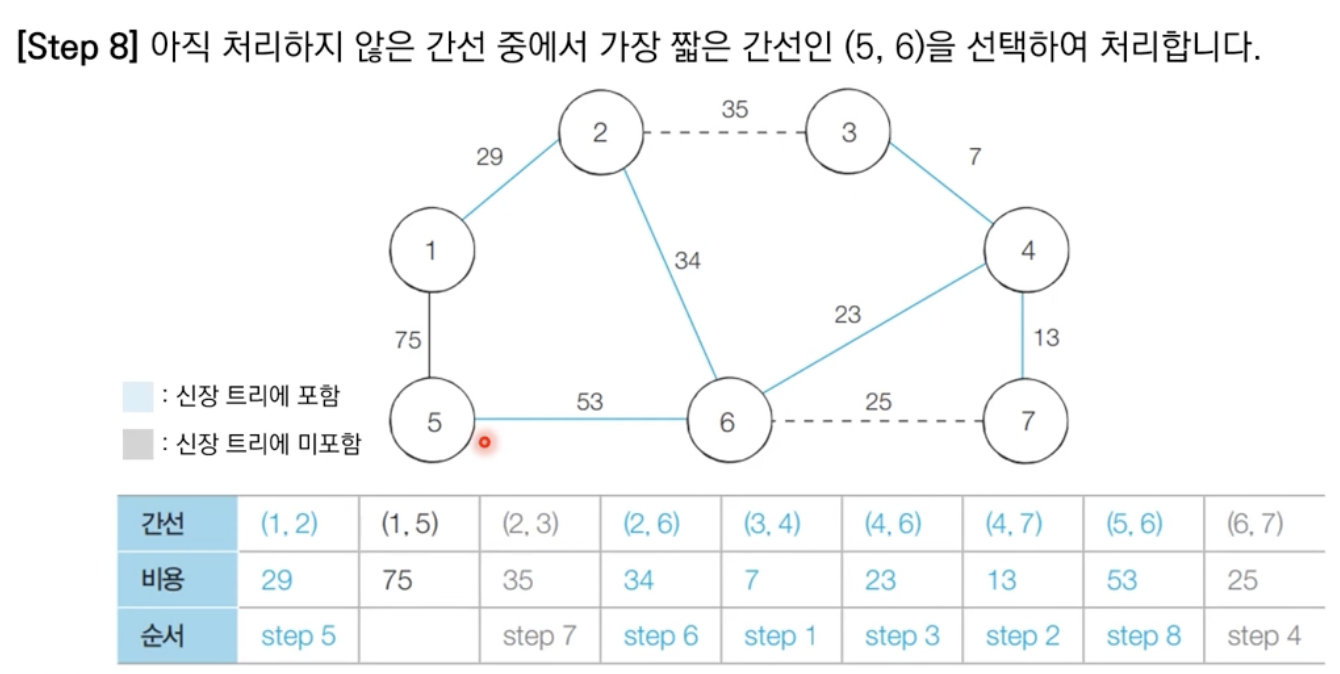
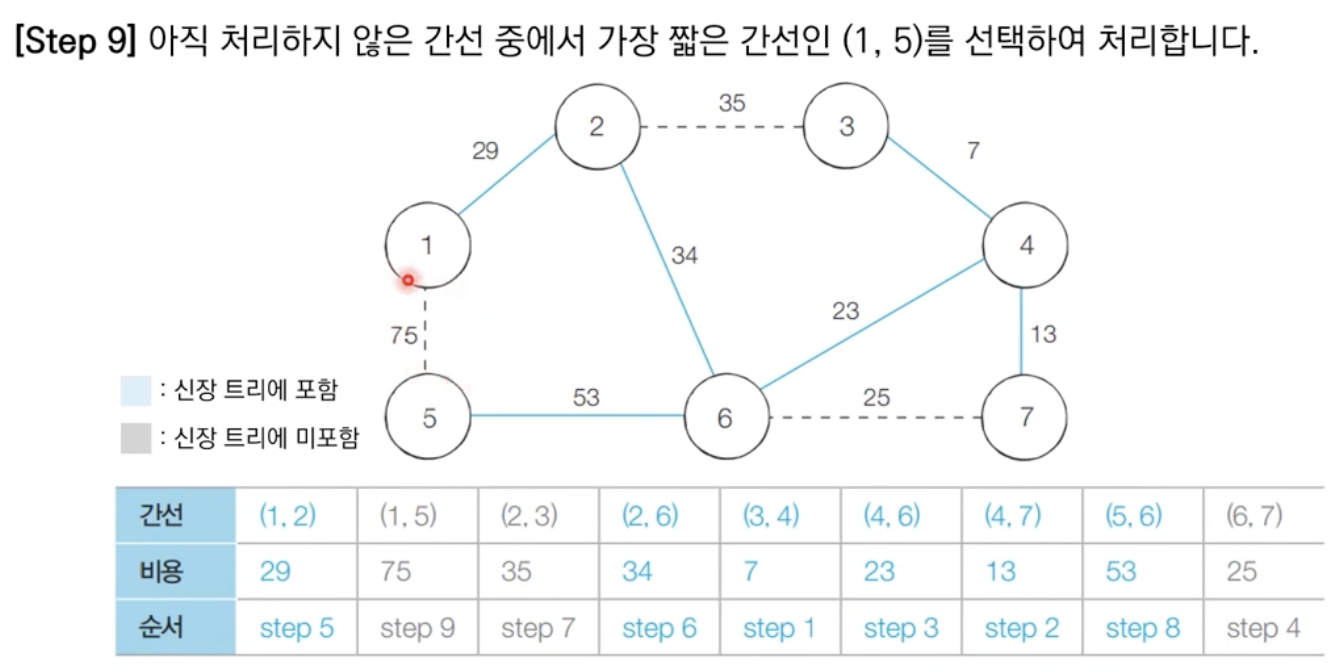
알고리즘 수행 결과

최소 신장 트리에 포함되어 있는 간선의 비용만 모두 더하면, 그 값이 최종 비용에 해당한다.

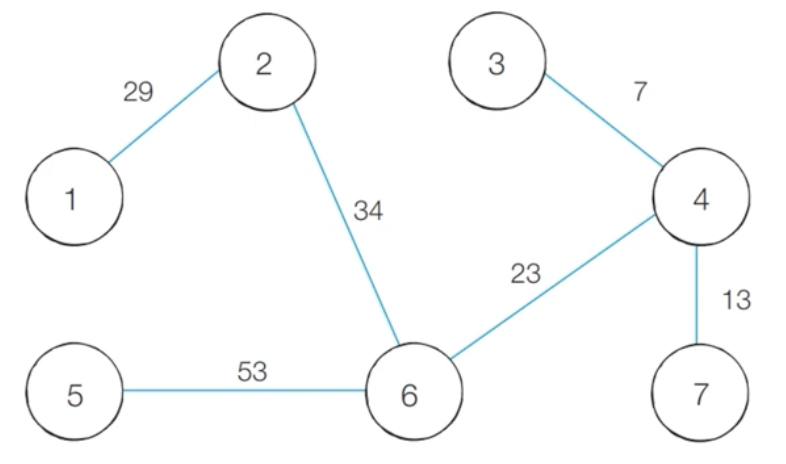
👩🏻‍💻 Kruskal 코드

import java.util.*;

class Edge implements Comparable<Edge> {

    private int distance;
    private int nodeA;
    private int nodeB;

    public Edge(int distance, int nodeA, int nodeB) {
        this.distance = distance;
        this.nodeA = nodeA;
        this.nodeB = nodeB;
    }

    public int getDistance() {
        return this.distance;
    }

    public int getNodeA() {
        return this.nodeA;
    }

    public int getNodeB() {
        return this.nodeB;
    }

    // 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Edge other) {
        if (this.distance < other.distance) {
            return -1;
        }
        return 1;
    }
}

public class Main {

    public static int v, e;
    public static int[] parent = new int[100001]; 
    public static ArrayList<Edge> edges = new ArrayList<>();
    public static int result = 0;

    public static int findParent(int x) {
        if (x == parent[x]) return x;
        return parent[x] = findParent(parent[x]);
    }

    public static void unionParent(int a, int b) {
        a = findParent(a);
        b = findParent(b);
        if (a < b) parent[b] = a;
        else parent[a] = b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        v = sc.nextInt();
        e = sc.nextInt();

        for (int i = 1; i <= v; i++) {
            parent[i] = i;
        }

        for (int i = 0; i < e; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int cost = sc.nextInt();
            edges.add(new Edge(cost, a, b));
        }

        Collections.sort(edges);

        for (int i = 0; i < edges.size(); i++) {
            int cost = edges.get(i).getDistance();
            int a = edges.get(i).getNodeA();
            int b = edges.get(i).getNodeB();
            if (findParent(a) != findParent(b)) {
                unionParent(a, b);
                result += cost;
            }
        }

        System.out.println(result);
    }
}