투빅스에서 두번째 심화 세미나로 생성모델을 하게 되었다. 지난 컨퍼런스 때 생성모델을 다뤘던 것이 개인적으로 재밌기도 했고, 무엇보다 생성모델이 데이터를 생성하는 분야 뿐만 아니라 텍스트에서 self supvervised learning과 연관이 있는 것 같아 배워두고 싶었다. 이번에 우선 Gan과 DCGAN에 대해 발표를 맡아 관련 자료를 정리하고자 한다.
0. Background/VAE

GAN에 대해 이야기하기에 앞서 몇가지 정리를 하고 시작하자. 지난주의 VAE나 이번 주의 GAN이 달성하고자 하는 목표는 그리 거창한 것이 아니다. 두 모델은 생성 모델을 시작하면서 흔히 접하는 DALL-E처럼 "마늘로 만든 펭귄"처럼 말도 안되는 문장을 넣어도 그에 맞는 이미지를 만들어주는 생성 모델이 아니다. 단순히 정해진 범위 내에서 현실과 비슷한 그럴 듯 하면서 조금씩 다른 이미지를 만들 수 있는 모델이다. 예를 들어 강아지 사진들을 이용해 GAN이나 VAE를 학습시키면 학습된 강아지 사진들과 조금 다르지만 어쨌든 지구 상에 언젠가 한번쯤 존재했을 법한 강아지 사진 1000장을 만들어주는 것이 두 모델의 목적이다.
이를 위해서는 생성모델의 측면에서 두가지가 필요하다.
- 생성된 이미지의 질을 판단할 수 있는 평가지표
- 조금씩 다르게 이미지를 만들 수 있는 입력값
지난주에 다루었던 VAE의 경우 1번을 결국 ELBO와 KL Divergence라는 지표를 이용해 MLE로 해결했다. 2번은 가우시안 등의 분포를 가정하고 여기에서 샘플링하여 그럴듯하면서 학습 이미지와 조금은 다른 이미지를 만들어낸다.
1. GAN(Generative Adversarial Net)
1-1. Intro
하지만 VAE의 KL Divergence나 ELBO가 정말로 생성된 이미지와 실제 이미지를 구별하는 좋은 지표일까?

물론 논문에서 이야기했듯이 위의 그림처럼 MSE보다야 좋은 지표임에는 틀림이 없다. 하지만 MNIST라는 흑백의 단순한 데이터에서 벗어나보자.

사람의 얼굴 데이터셋을 이용해 VAE를 학습시켰을 때의 결과들이다. 생각보다 매우 흐릿하고 남자의 얼굴에 긴 머리가 보이는 등 현실적이지 않은 이미지를 생성한다(물론 남자가 머리가 길 수도 있지만 저 사진은 어색하다.).
이는 위에서 설명한 생성모델의 두가지 요소에서 원인을 찾을 수 있지 않을까? 1. 평가지표가 완벽하지 않다. 단순히 ELBO 등을 통해 이미지의 복잡한 특징에 대한 평가를 할 수 없다. 2. 임의의 분포에서 생성한 latent vector가 충분히 이미지의 매니폴드를 포함하지 못하고 있다.
GAN은 그래서 두가지 요소를 다르게 구성하고 있다(실제 GAN 논문에선 VAE에 대한 언급은 없다.).
- DNN으로 구성한 Classifier를 통한 평가
- 정규분포에서 노이즈만 추출하여 입력값으로 사용
1-2. Model Architecture
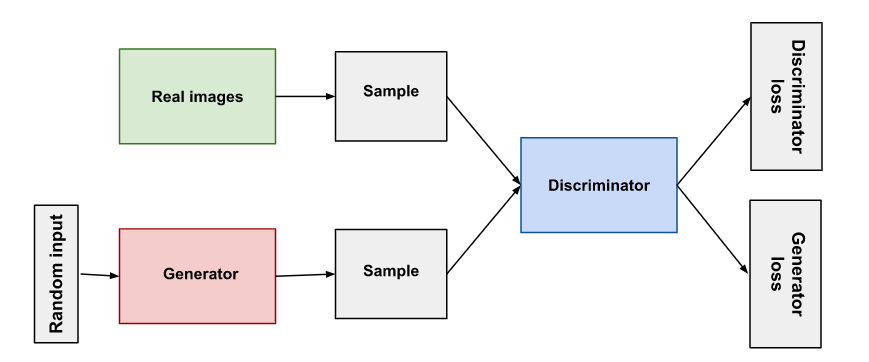
GAN의 전체 구조는 위와 같다. 임의의 벡터를 입력값으로 하고 Generator를 통과한 Sample과 실제 이미지인 Sample을 Discriminator의 입력으로 하여 출력된 예측값을 토대로 Generator와 Discriminator의 로스값이 정의되고, 이를 바탕으로 역전파가 일어난다. 복잡하니까 하나씩 보겠다.
1-2-1. Input
생성자(Generator)의 입력값은 정규분포에서 샘플링한 임의의 벡터이다. 이는 학습 과정에서 지속적으로 변화한다. 즉, 매 배치, 매 샘플마다 다른 값을 가진다. 이때 VAE와 달리 실제 이미지에서 추출한 분포가 아니다. 평균과 분산이 고정된 정규분포에서 추출한다. 이로인해 입력값은 이미지의 latent vector라기 보다는 노이즈로서 작용한다고 한다.
1-2-2. Generator
생성자는 임의의 벡터를 입력으로 받아 이미지를 생성하게 된다. GAN 논문 자체에서는 FFNN을 통해 이 과정을 수행한다.
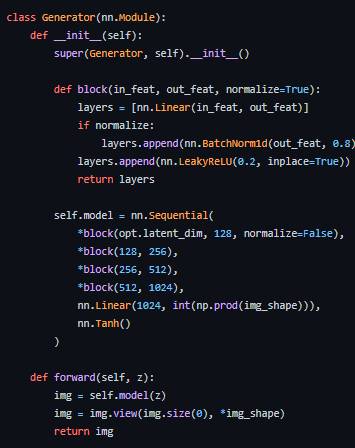
위 코드에서도 볼 수 있듯이 정말 그냥 벡터를 입력으로 받고 이 벡터의 사이즈를 이미지의 세로가로로 늘려서 reshape하여 이미지를 만들어낸다. generator는 128차원의 벡터를 256256 차원의 벡터로 mapping하는 역할을 한다고 볼 수 있다.
이게 가능한 이유는 아래 그림을 통해 설명할 수가 있다.
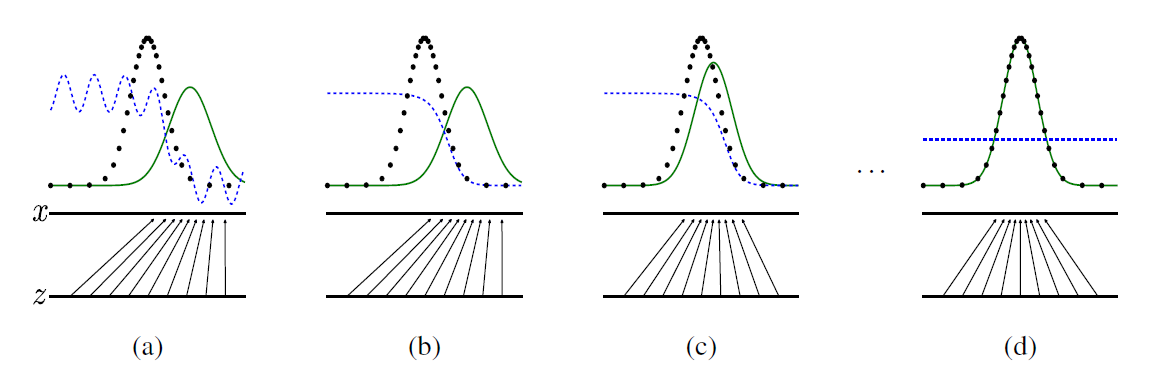
실제 이미지가 가지는 분포는 검은 점선, generator가 생성하는 이미지의 분포는 녹색 실선으로 표시되어 있다. x가 실제 이미지의 분포이고, z가 입력 벡터이다. 우리는 고정된 분포에서 입력 벡터를 추출하게 되는데, 이렇게 추출된 벡터는 실제 이미지의 벡터와 다른 분포를 가질 수 밖에 없다. 입력 벡터에 대해 generator가 mapping하여 실제 이미지의 차원으로 맞추어 가는 것이다.
1-2-3. Discriminator
판별자(Discriminator)는 실제 이미지와 생성자에 의해 생성된 이미지를 입력으로 받는다. 두 이미지를 동시에 받는 것이 아니라 그냥 이미지를 입력으로 하여 이진분류 태스크를 수행하는 모델인데, 실제 이미지와 생성된 이미지가 하나의 배치에 속한다고 간주하고 입력으로 받는다. 이제 우리는 입력 데이터(실제 이미지, 생성된 이미지)와 레이블(실제, 생성)을 모두 가지고 있기 때문에 지도학습을 할 수 있다. 지도학습을 통해 판별자는 실제 이미지와 생성된 이미지를 분류하는 역할을 하게 된다.
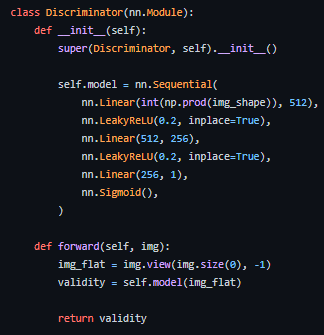
코드 상으로 보면 그냥 이미지 분류 모델을 처음 만들 때 배우는 방식으로 구성되어 있다. 2차원의 이미지를 flatten하여 1차원 벡터로 만들고 이를 FFNN 레이어를 통과시켜 분류하게 된다.
1-2-4. Objective Function
GAN의 목적함수는 다음과 같다.
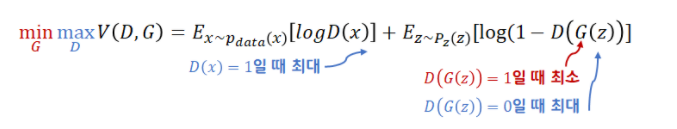
여기서 D는 판별자, G는 생성자이다. 실제 데이터의 분포인 에서 추출된 실제 이미지 와 임의로 고정한 분포인 에서 추출한 입력 벡터 를 활용해 식이 구성되어 있다. GAN은 min max 게임을 한다고 표현하는데 이를 분리해서 살펴보자. 이를 분리해서 생성자와 판별자의 관점에서 살펴보면 위의 그림에서 보았던 generator loss와 discriminator loss가 나오게 된다.
판별자 관점
판별자 관점에선 위의 목적함수를 최대화하는 문제가 된다. 위 식을 풀어서 살펴보자. 이때 앞의 항은 실제 이미지를 판별자에 넣었을 때 최대한 큰 값이 나와야 하고, 뒤의 항은 생성된 이미지를 판별자에 넣었을 때 최대한 작은 값이 나와야 한다. 즉 판별자는 실제 이미지에 대해 1에 가까운 값을 출력해야 하고, 생성된 이미지에 대해서는 0에 가까운 값을 출력하도록 학습해야 한다.
이진 분류 문제에선 BCE를 사용하여 손실함수를 구성한다. 판별자의 손실함수는 다음과 같이 구성될 것이다.
생성자 관점
생성자 관점에서는 판별자가 실제 이미지를 어떻게 판별하는지는 중요하지 않다. 오직 생성된 이미지가 실제 이미지로 판별되는지 여부만 중요하다. 즉, 생성자는 판별자가 생성된 이미지(y = 0)에 대해 실제 이미지처럼 판별하도록()록 학습되게 된다. 식으로 보면 다음과 같을 것이다. 다음 식을 최소화하는 방향이다.
본래 식은 여야 한다. 하지만 이런 식으로 학습하게 되면, 학습 초기에 문제가 생긴다. 학습 초기에는 생성자가 제대로 된 이미지를 생성해내지 못하여 가 0에 근사하게 되는데, 그렇게 되면 loss가 0에 가까운 값을 내게 되고, 그래디언트가 0에 가까워진다. 본래 식 역시 최소화하는 방향으로 학습이 진행됨을 기억하자.
그래서 식을 약간 변형하여 위와 같이 구성했는데, 이를 통해 가 0에 가까운 값을 낼 때 그래디언트가 커지도록 만들었다. 다만, 이는 증명된 사항이 아니라 실험을 통해 이렇게 하니 학습이 잘되더라 하는 내용이다.
1-2-5. 학습과정
GAN은 결국 생성자와 판별자를 학습시키는 과정이다. 물론 생성자를 만들어서 사용하려고 판별자를 더불어 사용할 뿐이다. 이때 위에서 언급한 이야기를 다시 생각해보면, VAE는 특정 평가 지표를 사용하여 실제 이미지와 생성된 이미지를 비교하지만 GAN은 결국 판별자라는 제 2의 모델이 생성된 이미지에 대한 평가를 맡고 있다. 생성자의 목표는 결국 실제 훈련에 사용되는 이미지와 유사한 이미지를 만들어내는 것이다. 이는 판별자가 생성자가 만든 이미지와 실제 훈련 이미지를 구별해내지 못하는 상황에서 달성된다고 할 수 있다. 즉, 생성된 이미지와 실제 이미지에 대해 모두 0.5의 확률을 출력하는 상황이어야 한다.

위 그림을 다시 살펴보면, a에서 d로 갈수록 학습이 이뤄지는 것이다.
(a) 생성자가 z를 입력으로 받아 만들어낸 이미지의 분포가 실제 이미지의 분포와 아직 많이 다르다. 그래서 판별자(파란 점선)이 두 이미지를 구별해내고 있는 모습이다.
(b) 판별자가 먼저 학습이 이루어져서 a에서보다 더 잘 분류하는 모습을 보이고 있다.
(c) 생성자가 학습을 통해 실제 이미지의 분포와 비슷한 이미지를 생성해내는 모습이다.
(d) 생성자가 실제 이미지와 완전히 비슷한 이미지를 생성해내기 시작하면 판별자는 결국 구분하지 못하고 모든 이미지에 대해 0.5의 확률을 내뱉게 된다.
결국 한 미니 배치 내에서의 학습 과정은 다음과 같다.
- z를 이용해 생성자에서 이미지 G(z) 생성
- G(z)와 실제 이미지 x가 판별자에 입력되어 각 이미지에 대한 예측값 생성
- 예측값을 이용해 생성자와 판별자 loss 계산
- 를 이용해 생성자 업데이트
- 를 이용해 판별자 업데이트
하지만 일반적으로 생성 태스크가 이진분류 태스크보다 난이도가 높을 수 밖에 없다. 이로인해 판별자가 먼저 학습이 빠르게 이루어지는 문제가 발생한다. 판별자의 성능이 지나치게 높아 거의 모든 이미지를 완벽하게 분류해내면, 생성자의 loss인 는 무한대로 발산해버려 더이상 학습이 불가능해진다. GAN의 안정적인 학습을 위해서는 생성자와 판별자가 비슷하게 학습이 이루어져야 한다. 이를 위해 일반적으로 생성자를 3 ~ 7회 업데이트 하고 판별자를 1회 업데이트하는 등의 방식이 자주 사용된다.
1-3. 증명
개념적으론 GAN이 어떻게 학습이 진행되는지 알았다. 그런데 정말 그렇게 학습이 진행될까? D와 G가 수렴하면, 정말로 G는 실제 데이터와 유사한 데이터를 만들도록 학습이 되고, D는 실제 데이터와 생성된 데이터를 구분하도록 학습이 진행될까? 딥러닝은 블랙박스인데, 우리가 모르는 이상한 방향으로 학습을 하지 않을까? 논문에서는 이와 관련하여 계산들을 실어놓고 있다.
우선 아래의 수식들은 다음과 같은 노테이션을 따른다.
- : 실제 데이터의 확률밀도함수
- : G의 입력 벡터의 확률밀도함수
- : 실제 데이터 분포를 따르는 데이터
- : 파라미터 에 대한 입력벡터 로 생성된 데이터
- : 에 의해 생성된 데이터의 확률밀도함수
- : D의 입력값으로 사용된 데이터 가 실제 데이터일 확률
- : 수렴 상태의
와 에 대한 value function은 다음과 같다.
위 수식에 대한 minmax 게임을 계속 반복하면서 결국 최종적으로 와 가 동일하도록 만드는 것이 우리의 목적이다. 즉, 학습이 완료된 상황에서는 임을 명심하자. 논문에서는 이 내용에 대한 증명 역시 실려 있는데, 아직 이해하기 힘들다... 우선 이것이 증명되었다는 가정 하에 다음 증명을 살펴보도록 하자. 즉, 이제 우리는 충분한 학습을 통해 G와 D는 으로 수렴함을 증명할 것이다.
1-3-1. Discriminator
는 다음과 같이 구할 수 있다.
그런데 여기서 우리는 임을 알기 때문에 다음과 같이 표기할 수 있게 된다.
여기서 조금 많이 까다로운데 변분법이 등장한다. 우리는 이제 위의 함수를 로 미분해야 한다. 위 함수를 최대로 하는 를 찾아야 하는데, 자체가 함수라는 문제가 발생하는 것이다. 당장에 이해하기에는 해석학에 대한 이해가 필요해서 자세한 이해와 설명이 부족한 점이 너무 아쉽다. 결과적으론 우린 결국 위의 식에서 내부의 식을 미분하였을 때 0이 되도록 하는 를 찾으면 된다. 즉, 다음과 같이 풀이가 이어진다.
즉, 이 된다. 여기서 다시 임을 상기해보면 이 될 것이다. 충분히 학습이 이뤄지면 는 실제 데이터와 생성된 데이터를 구분하지 못한다!
1-3-2. Generator
자 이제 의 실제 값도 구했겠다. 이를 이용해서 G의 식을 표현해보도록 하자. 우선, G의 입장에선 다음 식을 최소화하는 문제가 된다.
가 된다. 식이 복잡해보이는데, 저 식 결국 JS Divergence 혹은 두개의 KL Divergence이다.
KL Divergence나 JS Divergence나 결국 두 분포의 차이를 측정하는데 사용된다. 여기서 조금 아쉬웠던 점은, G가 인 식을 최소화하지 않는다는 점이었다. 아무래도 KL Divergence가 실제 분포를 기준으로 거리를 측정하기 때문에 직관적으로 더 정확한 식이 될 수 있지 않나 싶다. 그래도 는 학습 데이터 내에서 변하지 않는 분포이기 때문에, JS Divergence를 사용해도 큰 무리는 없을 것 같다. 를 최소화하기 위해서 가 에 가까워지도록 이동하도록 학습될 것이기 때문이다. KL Divergence나 JS Divergence에 대한 자세한 설명은 여기에 설명해놓았으니 참고바란다.
2. DCGAN
잠시만 생각해보면 GAN은 단순하게 FFNN 레이어로 이미지를 다루고 있다는 것을 알 수 있다. 그러면 당연히 드는 생각이 convolution 레이어를 사용해서 이미지를 만드는게 더 좋지 않을까? 더군다나 CNN 모델들은 계층적으로 이미지에 접근하기 때문에 곡선, 직선 등의 아주 작은 특징에서부터 질감이나 물체의 전체적인 모습 등 큰 특징을 잡아나가게 된다.
이를 이용하면 시각적으로 GAN류 모델이 잘 학습되고 있는지, 혹은 우리가 생성 모델을 컨트롤할 수 있는지 알 수 있게 될 것이라는 생각에서 나온 논문이 DCGAN이었다. DCGAN과 GAN의 차이점은 생성자와 판별자를 DNN에서 CNN으로 바꾼 것 뿐이다. 이를 하나씩 살펴보도록 하자.
2-1. Generator
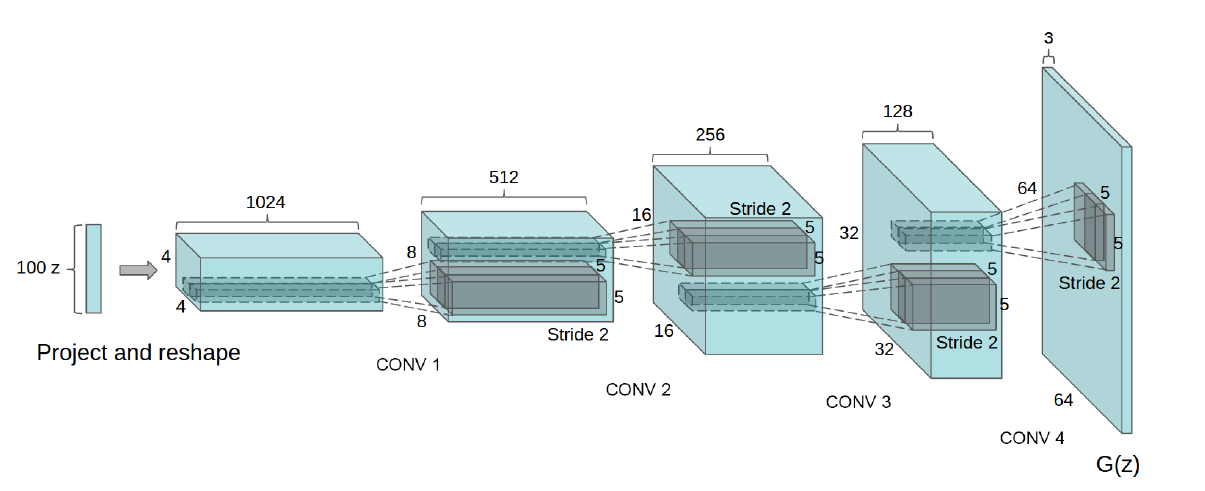
DCGAN의 생성자는 위와 같은 구조를 가지고 있다. 임의로 생성된 벡터 z에서 출발하여 우리가 원하는 이미지 크기인 64643의 텐서를 만들고 있는 것을 볼 수 있다. 여기서 잠깐 이상한 점은 우리가 아는 Conv 레이어는 입력 크기보다 작은 크기의 출력값을 만들어낸다는 점이다. 그런데 위의 이미지에선 입력 크기의 2배에 해당하는 크기가 계속 출력되고 있는 것을 알 수 있다. 어떻게 가능한 것일까?
2-1-1. Transposed Convolution
바로 일반적인 convolution 레이어가 아니라 Transposed Convolution을 사용했기 때문에 가능하다. Transposed Convolution의 작동원리는 다음과 같다.
(블로그 글로 이동하여 보기)
이를 통해 입력 크기보다 큰 크기를 가지면서 가중치를 공유하는 Convolution 레이어가 된다.
2-2. Discriminator
판별자는 우리가 아는 이미지를 입력으로 받아 이진분류 태스크를 수행하는 CNN 모델이 사용되었다. 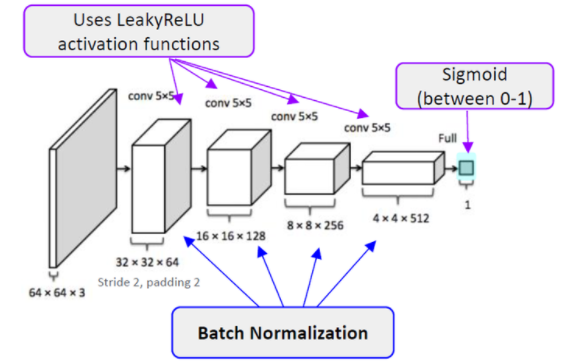
2-3. Result
결과에 대해 조금 이야기해보도록 하자.

1 에포크를 돌았을 때 생성된 이미지들의 모습이다. 생성모델에서 종종 언급되는 것이 모델이 단순하게 실제 데이터를 모방하고 있는 것에 대한 우려이다. 즉, 우리는 그럴듯한 이미지를 만들어야지 실제 이미지를 생성하는 모델을 만들면 안된다. 이는 학습한다기 보다는 기억하는 모델이기 때문에 학습 데이터에 과적합된 상태이기 때문이다. 그런데 위 이미지들은 1 에포크만 돌았기 때문에 생성자가 아직 실제 이미지에 대해 과적합되어있지 않은 상태인데도 그럴듯한 침실 이미지를 생성해내는 모습을 볼 수 있다.

5 에포크를 돌고 나면 더 그럴듯한 모습의 이미지가 생성되는 것을 볼 수 있다.
GAN은 또한 입력 벡터 z를 취하고 있고, 이는 우리가 자유롭게 조정이 가능한 부분이다. 이를 통해 이미지를 부분적으로나마 조작할 수도 있다.

위의 이미지는 z의 한 값을 연속적으로 변화시켰을 때 얻어지는 이미지들인데, 자세히 살펴보면 침대가 사라진다거나 창문의 위치가 움직인 모습을 볼 수 있다. 이는 z가 노이즈로서 훌륭한 역할을 하고 있다는 뜻으로 z의 공간에서의 이동이 실제 이미지에서도 유의미한 변화로 나타나고 있는 것을 알 수 있다.

또한 이미지는 z를 실제 데이터의 분포인 에 맵핑하는 생성자에 의해 생성된다는 점을 생각해보면, 특정 이미지를 생성하는 생성자의 필터가 존재한다고 생각할 수 있다. 예를 들어 위의 이미지는 창문을 생성한다고 추정되는 필터를 제거한 상태에서 생성자가 생성한 이미지들인데, 창문이 커튼으로 가려져있거나 벽으로 변하는 등의 모습을 보이고 있다. 즉, 생성자가 z를 로 맵핑하는 역할을 잘 수행하고 있다고 할 수 있을 것이다.
2-4. Face
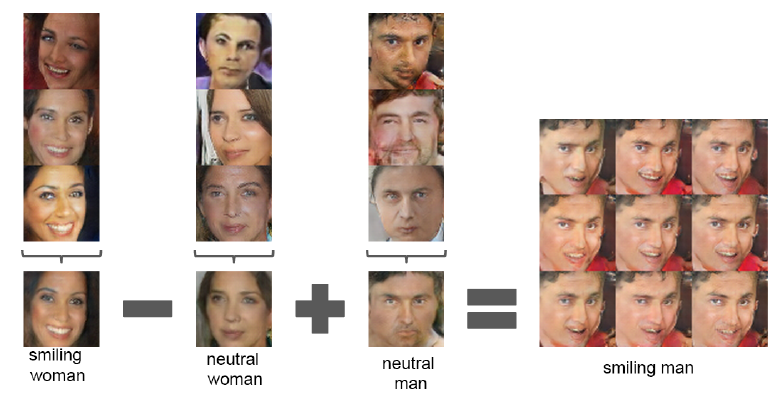
위에서 z의 이동을 통해 이미지를 변화할 수 있다고 했는데, 이를 극단적으로 보여주는 사례가 위와 같다. 웃는 여성의 얼굴을 만들어내는 z들의 평균값에서 무표정인 여성의 z를 빼고, 무표정의 남성의 z를 넣으면 웃는 남성의 얼굴이 생성되게 된다.
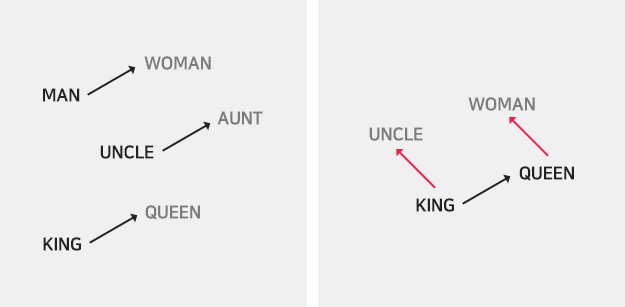
위와 같이 벡터 공간에서의 연산이 유의미한 것을 보여준다고 할 수 있다.
3. Conclusion
결국 GAN은 오토인코더의 디코더 구조만 떼어다가 학습시킬 방법을 고민한 모델이라고 할 수 있다. 그 과정에서 실제 데이터의 분포를 추정하지 않고도 실제 데이터에 근사하는 mapping function을 만들 수 있다는 것을 보여주었다. VAE와 비교해보자면 VAE는 GAN에 비해 분명한 지표를 가지고 있어 모델 간 성능 비교가 간편하다는 점이 있다. GAN은 성능 평가 지표가 없기 때문에 다른 모델 간의 비교가 초기에는 매우 힘들었다고 한다. 하지만 GAN은 실제 분포를 가정하지 않고 데이터를 생성하기 때문에 더 그럴듯하고, 매우 깔끔한 이미지를 만들어낸다고 한다. 이를 Yoshua Bengio는 GAN은 실제 분포와 조금 다르더라도 더 뾰족한 분포를 생성하기 때문에 그럴듯한 이미지가 되는 반면, VAE는 실제 분포와 유사하지만 mle 자체가 분포를 옆으로 퍼트려 버리는 바람에 실제 이미지와 다른 이미지가 생성된다고 이야기한다.
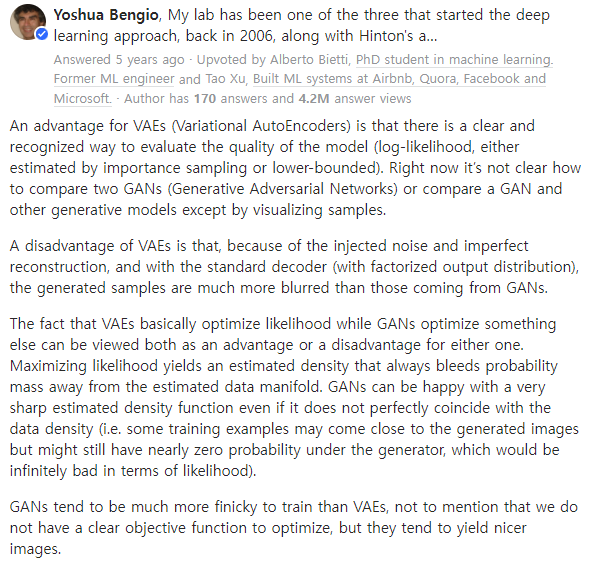
참고
Pytorch로 다양한 생성 모델을 구현한 깃허브
Google에서 제공하는 GAN에 대한 간략한 설명
다양한 Conv 레이어 소개글
라온피플의 DCGAN 설명
Yoshua Bengio의 이야기
GAN에 대한 수식적 설명 블로그1
GAN에 대한 수식적 설명 블로그2
ratsgo님의 GAN 설명글
GAN & DCGAN 논문
