[CS224N] Lecture 2 - Word Vectors and Word Senses

김재희·2021년 4월 17일

CS224N

목록 보기

2/15

저번 시간엔 자연어 처리에서 가장 기본적인 입력값(x)이라 할 수 있는 워드 임베딩의 기본적인 개념에 대해서 배웠다.

워드 임베딩의 장점은 명시적으로 보이는 의미 관계뿐만 아니라 단어 간의 복잡한 의미 관계를 벡터 공간에 표현할 수 있다는 것이다. (정확하게는 임의의 알고리즘에 의해 포착하니 표현된다고 이야기해야 할 것 같다.)

위 이미지는 시대에 따른 각 단어들의 의미 변화를 표현하고 있다. gay의 경우 처음엔 패션이나 맛을 나타내는 단어들과 비슷한 뜻을 가지다가, 점차 성소자를 지칭하는 단어로 사용되면서 lesbian과 비슷한 뜻을 가지게 된 것을 볼 수 있다.

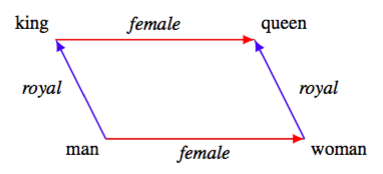
혹은 위처럼 king에서 man의 의미를 빼고, woman의 의미를 더하면 queen의 의미를 지칭하는 벡터가 되는 것처럼 선형 관계를 이루고 있는 것을 알 수 있다.

king과 queen의 사례에서 보면, 문자형 자료로서 둘 간은 전혀 비슷하지 않다. 하지만 이 단어들과 매칭되는 (word2vec에서 context vector에 해당하는) 임베딩 벡터들은 이러한 전혀 다르게 보이는 단어들의 의미를 정확하게 포착하고 있다. king 과 queen의 차이가 man과 woman의 차이와 같다고 벡터 공간 상에 나타낼 수 있게 된 것이다. 그리고 다양하고 복잡한 단어 간의 의미관계를 임의의 100차원 이상의 공간으로 수많은 단어에서 포착할 수 있다는 것은, 충분히 복잡한 모델을 돌릴 수 있게 되었다는 말이다. 데이터의 품질이 좋아지니, 당연히 분석의 다양성 역시 높아질 수 있다. 혹은 다양한 활용이 가능할 것이다(이를테면 챗봇).

Word2Vec의 문제점

word2vec을 잠깐 다시 짚고 넘어가자면, 중심단어와 주변단어를 내적과 소프트맥스를 이용해 서로를 예측하는 단순한 모델을 구축하고, 이를 코퍼스 내의 모든 단어에 대해 반복하여 임베딩 벡터를 구하게 된다.
사실 이 아이디어는 너무 단순해서 아직도 이게
꽤 엄청 많이 잘 작동한다는게 믿기지 않는다. 사실 word2vec을 좀 더 살펴보면 성능을 개선할 여지가 있다.

1. 단어 등장 빈도 의존

and, so, of, the와 같이 무척 많은 단어들과 자주 함께 사용되는 단어들의 경우에는 의미가 없음에도 불구하고 정말 자주 연산이 발생하고 실제로 어떤 의미를 지니고 있는 것처럼 처리된다. 또한, 실제로 의미가 있는 단어라 할지라도, 그 사용빈도에 따라 임베딩 벡터가 업데이트되는 빈도가 달라져서 결국 임베딩의 성능이 단어의 등장 빈도에 달려있게 된다.

2. 업데이트 방식

1강에서 살펴보았던 word2vec의 업데이트 식을 보면, 해당 업데이트에 사용되는 단어들만 그래디언트가 존재하는 것을 알 수 있다. 그런데 전체 학습은 SGD를 비롯하여 배치학습으로 이루어진다. 그러면, 배치 학습에서 나타나지 않은 단어들은 사실 학습이 되지 않음에도, 여전히 연산이 이루어지는 것이다(0.3445*0 이런 식의 전혀 의미 없는 연산 말이다.). 가뜩이나 코퍼스도 크고, 단어도 많아서 연산이 오래 걸리는데, 필요없는 연산이 너무 많아진다.

U, V context vector

이건 내가 word2vec을 처음 배울 때부터 들었떤 의문인데, 강의를 들으면서 해결되었다. 이렇게 벡터를 두개를 만든 이유는 사실 단순하다. 계산이 편하다. 미분할 때 ab의 미분은 a 혹은 b가 되지만 aa의 미분은 2a가 된다. 그리고 만약 벡터 미분을 생각하면 더 복잡해진다. 어차피 이번 시점의 중심단어가 다음 시점의 주변단어로 사용되기 때문에, U와 V로 나누어도 충분히 하나의 벡터로 구할 때와 유사한 분포를 가진 벡터가 나온다고 한다. 그래서 보통은 두 벡터의 평균을 최종 벡터로 사용한다고 한다.

Word2Vec 디테일

1. 모델 종류

1-1 Skip-Gram

스킵 그램은 중심단어로 주변단어를 예측하는 모델이다. 이때 각 주변 단어의 위치는 예측에 독립적이라고 생각한다. 이전 강의에서 미분 했던 것이 skip gram의 식이다.

1-2 Continuous Bag of Words

CBOW는 주변 단어 각각을 독립이라 가정하고, 주변 단어로 중심단어를 예측하는 모델이다. 강의에선 자세히 설명하지 않았지만, 모델이 이진 분류 문제로 단순해지고, 더 많이 업데이트 할 수 있는 등의 이점으로 훨씬 질이 높은 임베딩 벡터를 얻을 수 있다고 알고 있다.

2. 효율 높이기

2-1 negative sample

샘플링이란 모집단에서 임의의 방법으로 데이터를 추출해내는 것을 의미한다. 그렇다면 네거티브 샘플링은 모집단이 아닌 데이터를 임의의 방법으로 추출하는 것이겠다. word2vec에선 주변실제 주변단어와 주변단어가 아닌 단어를 이진 분류를 통해 분류하는 모델을 구성하여 임베딩 벡터를 구한다. 이때 주변단어가 아닌 단어들은 임의의 분포를 가정하여 샘플링하게 된다. 해당 단어의 네거티브 샘플링 분포는 다음 식을 통해 정의된다.

$P(w) = {U(w)^{3/4} \over Z}$

이때 U(w)는 유니그램 카운트라고 하며 각 단어가 전체 코퍼스에서 등장한 횟수이다. 유니그램 카운트를 3/4 승하여 단어 간 유니그램 카운트의 차이를 줄여준다(27과 8 의 차이보단 3과 2의 차이가 작다). Z는 단순한 normalization term으로 모든 $U(w)^{3/4}$ 의 합이다. 이를 통해 P(w)는 단어들이 네거티브 샘플링될 확률 분포가 된다. 자주 등장하는 단어는 자주 네거티브 샘플링될 것이다.
그리고 이러한 경우의 목적함수는 다음과 같이 정의된다.

$J_{neg-sample}(o, v+c, U) = - log(\sigma(u_o^T*v_c)) - \sum_{k = 1}^{K}log(\sigma(-u_k^T*v_c))$

이때 우변의 좌항은 실제 주변단어 $u_o$ 이고, 우항은 네거티브 샘플링을 통해 나온 가짜 주변단어 $u_k$ 이다. K는 네거티브 샘플링할 단어라고 할 수 있다. 여기서 내가 놓쳤던 부분은 뒷항이 단순히 -가 붙어서 처리될 수 있는 이유였다. 사실 단순한데, sigmoid 함수가 0을 중심으로 대칭이기 때문에 1 - p(x) = p(-x)가 되고, 그러므로 뒷 항은 사실 주변단어가 아닐 확률을 최대화하는 항이 되는 것이다.

위 식을 미분하면 다음과 같이 되는데 하나씩 항을 살펴보자면

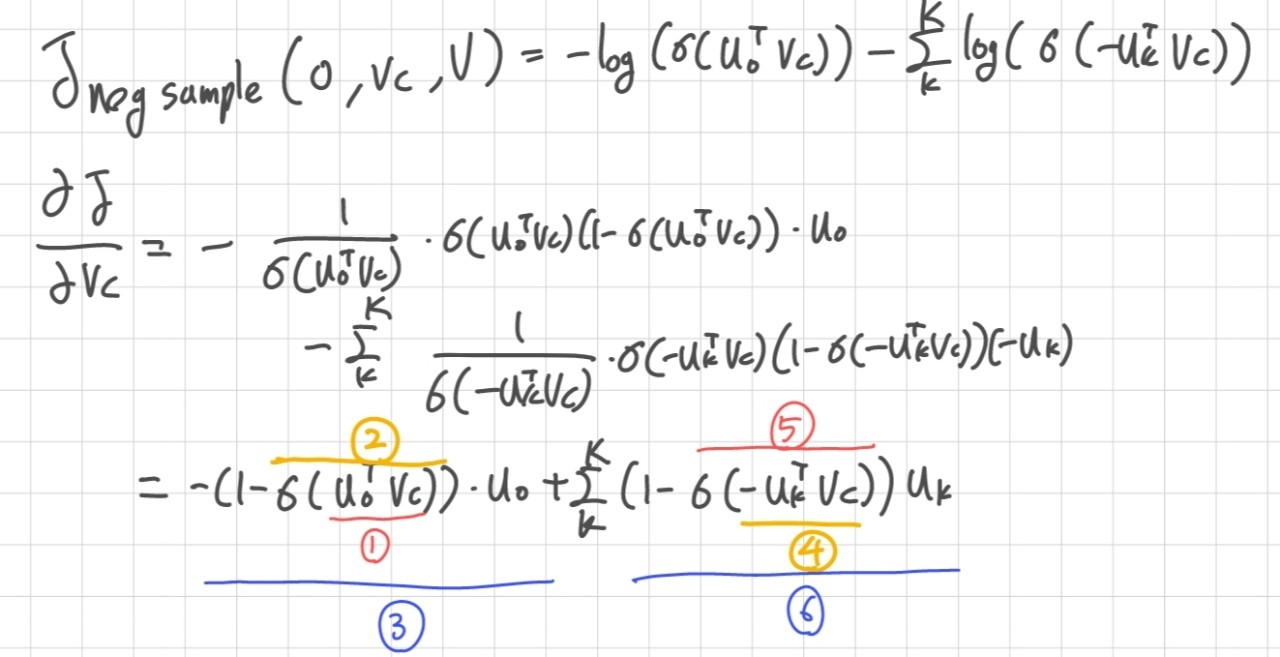
(1) 주변단어와 중심단어의 내적이다. 두 단어 벡터가 가까울 수록 0, 멀수록 1이 된다.
(2) 1에 시그모이드를 씌운다. 두 단어 벡터가 가까울수록 0.5, 멀수록 1이 된다.
(3) 1-(2) 식을 하여 $p(c \mid o)$ 가 된다. 그리고 이를 다시 $u_o$ 와 곱하기 때문에 기대값이 된다.
(4) 네거티브 샘플링 단어와 중심단어의 내적에 음수를 취한 항이다. 두 단어가 가까울수록 0, 멀수록 -1이 된다.
(5) 4에 시그모이드 함수를 취했다. 두 단어 벡터가 가까울수록 0.5, 멀수록 0이 된다.
(6) 1-(5)식을 하여 $p(c\mid neg sample)$ 이 된다.그리고 이를 다시 $-u_k$ 와 곱하기 때문에 기대값이 된다. 또한 이를 모두 더하기 때문에 전체 네거티브 샘플링의 기대값이 된다.

Glove

1. 배경

word2vec은 윈도우 방식을 사용한다. 하지만 이러면 위에서 상기한 단어등장빈도 의존의 문제점이 발생한다. 모델이 당장의 중심단어와 주변단어만 살피다보니 코퍼스 전체의 정보가 업데이트 시에 반영이 되지 않는 것이다. 코퍼스 전체의 정보는 통계를 통해 쉽게 찾을 수 있다. 흔히 배우는 동시등장 행렬(co-occurrence matrix)이 그것이다. 동시등장 행렬이란, 일정 크기의 윈도우 내에서 같이 사용된 단어들 간의 빈도수를 기록한 것이다. 이때 동시등장 행렬은 symmetric하고 sparse하다.

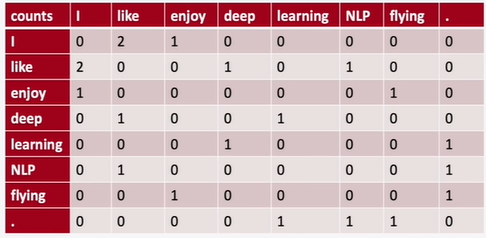
이 때 row 혹은 coumn 벡터를 그대로 임베딩 벡터로 사용할 수 있다. 하지만 말했듯이 sparse하기 때문에 매우 비효율적인 벡터이고 제대로 의미가 반영되지 않을 것이다.

word2vec은 윈도우 기반 모델로 코퍼스 전체의 정보를 포착하지 못하지만, dense하게 임베딩 벡터를 만들 수 있다.
동시등장 행렬은 전체 정보를 잘 포착하지만 너무 sparse하다.

이 둘의 특징을 합하면 dense하면서도 문서 전체의 정보를 잘 포착하여 임베딩할 수 있지 않을까? 이 아이디어를 구현한 것이 glove이다.

사실 동시 등장 행렬이 너무 sparse해서 문제라면 svd 등의 전통적인 행렬 분해 방식으로 dense하게 만들수도 있다(SVD를 비롯한 행렬 이야기는 나중에 기회가 되면 정리하자... 강의에 나온 내용은 너무 적고, 나머지를 다 적기엔 너무 글이 길어질 것 같다.).

2. 동시 등장 행렬 매만지기

하지만 위 행렬을 어떻게 임베딩에 사용할 수 있을까? 우선 단순히 동시등장 count를 사용하기 보단 동시등장 확률을 사용해보자. 예를 들어서 $P(solid \mid ice), P(gas \mid ice)$ 처럼 말이다.

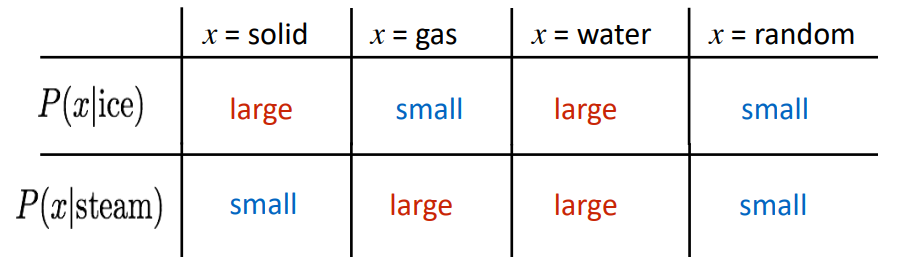
그럼 위와 같이 서로 관련이 높은 단어는 확률이 높게, 서로 관련이 적은 단어는 확률이 낮게 나올 것이다.
그리고 이 확률들을 이용해 비율을 계산해보면

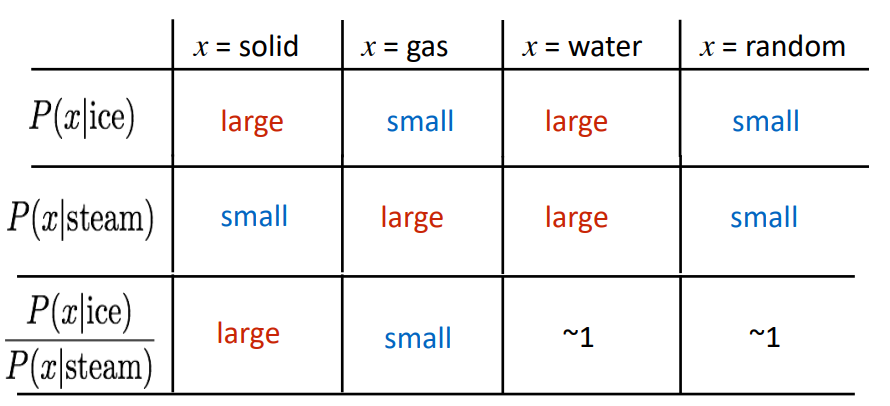
위와 같이 두 단어(ice, steam)과 모두 관련이 있는 단어나 모두 관련이 없는 단어는 1에 가깝고, 한 단어에만 관련이 있을 경우 1에서 멀어지는 것을 알 수 있다. 이때 단어간의 관계를 선형적으로 볼 수 있다고 말할 수 있지 않을까?

즉, 동시등장확률을 단어 벡터의 내적으로 표현하는 방법을 찾아야 한다!

3. 수학적 전개

식으로서 하나씩 풀어보자.

우리가 word2vec을 통해 얻은 것 : $w_i, w_j, w_k$ (이때 $w_k$ 는 중심단어)
우리가 동시등장확률 비로 얻은 것 : $P(k \mid i) \over P(k \mid j)$

이때 벡터 공간을 선형적으로 구성하고 싶기 때문에 다음과 같은 벡터 내적을 통해 식을 정리하는 것이 목표이다.
$F((w_i - w_j)^T w_k)$ = $P(k \mid i) \over P(k \mid j)$
임의의 함수 F를 통해 맵핑 시켜주는 것이다.
워드 임베딩을 위해서 F는 다음과 같은 성질을 만족하는 함수여야 한다.

단어 벡터간 교환 법칙 성립

동시등장행렬은 symmetric

homomorphism 만족

준동형 조건은 위 식에서 좌항이 빼기로 되어 있는데, 우항은 나누기로 되어 있기 때문에 이 변환을 위해 필요한 것으로 보인다. 위의 세가지 조건을 만족하는 함수는 지수함수가 있다. 이제 변환해보자.

$exp((w_i - w_j)^T w_k)$ = $exp(w_i^Tw_k - w_j^Tw_k)$
$exp(w_i^Tw_k - w_j^Tw_k)$ = $exp(w_i^Tw_k) \over exp(w_j^Tw_k)$
$exp(w_i^Tw_k) \over exp(w_j^Tw_k)$ = $P(k \mid i) \over P(k \mid j)$
$exp(w_i^Tw_k)$ = $P(k \mid i)$
짜잔, 두 벡터의 내적을 지수함수에 올리는 것만으로 동시등장 확률을 구하는 식이 되었다. 이제 이걸 좀 더 풀어보자. 사실 아직 풀이가 끝나지는 않았다.

$exp(w_i^Tw_k)$ = $P(k \mid i)$
$P(k \mid i)$ = $X_{ki} \over X_k$
$exp(w_i^Tw_k)$ = $X_{ki} \over X_k$
$w_i^Tw_k$ = $log({X_{ki} \over X_k})$ = $log({X_{ki}) - log(X_k})$

여기까지 오면 식이 1번 조건을 만족하지 않는다는 것을 알 수 있다. i와 k가 바뀔 경우, 즉 중심단어와 주변단어의 위치가 바뀌면 마지막 항인 $log(X_k)$ 가 바뀌기 때문이다. 이를 해결하기 위해 마지막 항을 $b_k$ 라는 편향으로 바꾼다. 또한 1번 조건을 만족하기 위해 $b_i$ 도 추가한다.
$w_i^Tw_k$ = $logX_{ki} - b_i - b_k$
$w_i^Tw_k + b_i + b_k$ = $logX_{ki}$
이제 식의 좌변엔 모델을 통해 구할 파라미터들이, 우변엔 코퍼스를 통해 얻을 수 있는 통계적 정보들이 오게 되었다. 즉, Glove는 통계적 방법론과 인공신경망을 이용한 방법론을 통합하여 임베딩하고자 했다. 손실함수를 구성해보자.

$J = sum_{i,j = 1}^{V}(w_i^Tw_k + b_i + b_k -logX_{ki})^2$

하지만 이렇게 하더라도 연구진은 한가지를 더 해결하고자 했던 것 같다. $X_{ik}$ 가 극히 적은, 그러니까 동시등장빈도수가 극히 적은 단어 조합이 대부분일텐데, 이런 애들은 사실 임베딩에 있어서 큰 도움이 되지는 않을 것이다. 우연히 같이 사용되었을 수 있기 때문이다. 이를 고려해서 weighting function을 추가했는데, 이때 단어 빈도가 일정 수 이상일 경우 똑같이 가중치를 주도록 하여 단어 빈도에 너무 영향을 받지 않도록 했다.
$f(x) = min(1, (x/x_{max})^{3/4})$

$J = f(x)\sum_{i,j = 1}^{V}(w_i^Tw_k + b_i + b_k -logX_{ki})^2$

4. 결과

결과적으론 통계적 모형과 인공신경망 모형을 결합하여 임베딩하였다는 의의가 있다고 할 수 있습니다. 또한 실제로 임베딩 결과의 평가지표들이 나쁘지 않았고요. 강의에선 평가지표에 대한 이야기가 좀 더 나오지만 현재 사용되는 평가지표들과는 또 다른 것 같아서 따로 정리하지는 않았습니다.
하지만 여전히 문제점은 있습니다. 동시등장행렬을 만드는게 여간 오래걸리는 일이 아닙니다. VxV크기의 행렬을 만들어야 하는데 정말 비용측면에서 부담이 되는 모델일 수 밖에 없습니다.

아직 강의 리뷰를 쓰는 것은 어색한 일인 것 같습니다. 1강은 그저 강의 내용을 정리하기만 했는데, 아무래도 강의이다 보니 논문 내용이 자세히 나오지 않고, 제 공부엔 조금 떨어진 내용들이 나오기도 했습니다. 강의를 베이스로 하되, nlp 전반을 정리하는 글을 쓸 수 있도록 해야할 것 같습니다.