0. 다중분류문제
다중 분류 문제를 푸는 가장 간단한 모델은 아마 소프트맥스일 것 같다. 해당 모델은 다음과 같이 생겼다.
0-1. 소프트맥스
그리고 이를 다시 풀어서 써보면 다음과 같다.
로짓 회귀에선 로 식이 마무리되지만 소프트맥스는 각 클래스에 대한 로짓회귀와 이를 normalization해주어 각 클래스에 대한 확률을 산출한다. 그래서 이를 다시 써보자면
0-2. 손실함수
그래서 여기서 파라미터인 W를 학습시키기 위해선 손실함수를 정의할 필요가 있다. 여기선 negative log loss를 사용하기 때문에 식은 다음과 같다. 위의 식에 -log를 붙인 것에 불과하다.
0-3. 크로스 엔트로피
이 식의 의미는 크로스 엔트로피라는 개념에 담겨있게 된다.
여기서 p는 실제 데이터의 분포이고, q는 우리의 모델이 만드는 분포이다. 분류문제에선 one hot encoding된 클래스와 각 클래스에 대한 확률 분포일 것이다. 이때, p를 일종의 가중치로 하여 q의 로그값을 더하게 된다. q의 범위는 0 부터 1까지이기 때문에 로그값을 씌워 부터 0까지의 값을 가지게 된다. 즉, 크로스 엔트로피의 값을 최대화하여 손실을 최소화하는 문제가 된다.
위의 설명은 각 인스턴스, row에 대한 설명이므로, 모든 인스턴스에 대한 로스를 합쳐보면 다음과 같은 식이 된다.
간단히 말하면, 각 인스턴스의 로스의 평균이라는 말이다. 로그 안의 항은 소프트맥스 함수이다.
만약 아래와 같은 식이 있다면,
를
로 표현할 수 있게 된다. x를 벡터로, 파라미터를 행렬로 표현한 것이다. 이렇게 행렬로 표현하면 나중에 미분하고 업데이트 시 행렬 단위로 통채로 연산할 수 있게 된다.
1. 데이터와 모델
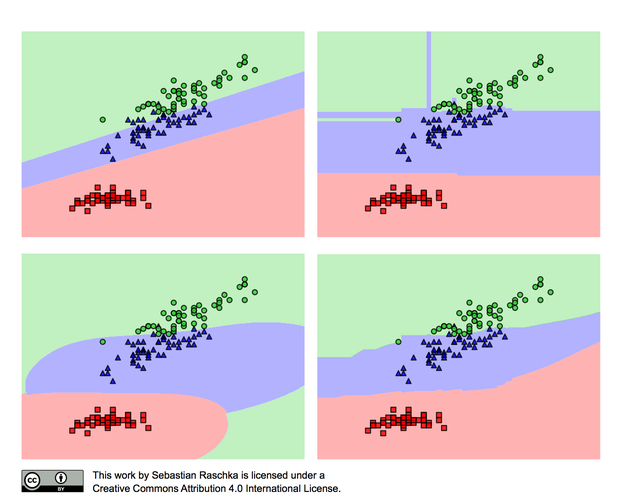
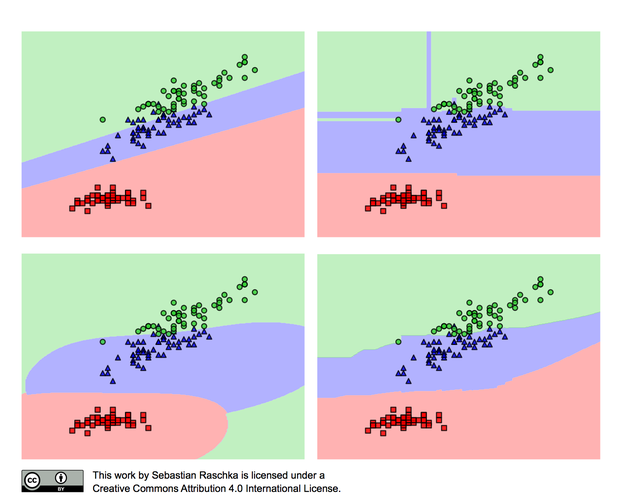
위 이미지는 모델과 데이터 복잡도에 따른 분류 성능을 시각화해놓은 것이다. 우선 데이터가 선형적으로 분리가 불가능하다. 초록색과 파란색 데이터가 어느정도 겹치는 부분이 있기 때문이다. 이는 단순한 선형 관계를 지니는 모델인 선형 회귀나 로짓회귀, 소프트맥스 함수를 이용해 완벽히 분류해낼 수 없다. 좀더 복잡한 랜덤포레스트, SVM 등의 모델이 필요하다. 하지만 항상 복잡한 모델이 좋은 것은 아니다. 모델이 복잡할수록 학습 데이터에 과적합되고, 새로운 데이터에 대한 성능이 급격히 떨어진다. 만약 위의 데이터에 트랜스포머나 U-net과 같은 수십억개의 파라미터를 가지는 모델을 사용한다면 당연히 성능도 좋을 수 없다. 이를 모델과 데이터의 bais variance trade off 관계라고 이야기 하는데, 피샛에서 배운 것들 중에 가장 많이 적용하고 고려하는 요소인 것 같다.
2. 자연어 처리 분야에서의 모델
자연어 처리 분야의 가장 큰 힘든 점은 그냥 자연어를 집어넣을 경우 정말 말도 안되게 큰 모델이 된다는 것이다.
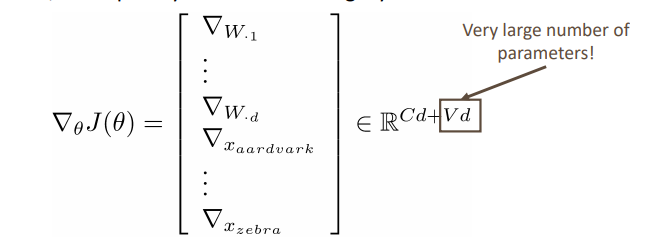
그래서 전에 배웠던 사전학습된 임베딩 벡터를 사용하거나 모델에서 임베딩을 학습하게 된다. 위의 사진은 모델에서 임베딩 벡터를 학습하는 것을 보여주는데 부터 까지의 모델의 파라미터와 각 단어들의 임베딩 벡터를 학습하는 모습을 볼 수 있다. 이때 문제점은 단어의 임베딩 벡터를 학습하자면, 모델의 파라미터가 기하급수적으로 늘어난다는 것이다. 위에 나타난 것처럼 Vxd가 되는데 보캡은 아무리 작아도 수천, d도 아무리 작아도 50은 된다는 것을 생각하면 정말 커지게 된다. 그래도 데이터만 충분하다면 이를 통해 단어들의 의미 표상과 모델을 학습할 수 있어서 좋다.
3. ANN(Artificial Neural Network)
사실 ANN이나 DNN, CNN, RNN은 정말 수없이 많이 봐서 강의에서도 스킵할까했지만 간단하게라도 정리하고 넘어가려고 한다.
사실 DNN이나 ANN을 기존의 통계적 관점에서 여러가지 해석이 가능할 것 같다. 어떻게 보면 Factor Analysis 같기도 하고, 어떻게 보면 여러 로짓 회귀를 이어놓은 것에 불과하기도 하다. 다른 점이 있다면, DNN이 되면서 FA와 다르게 각 항이 어떤 항인지 정하지 않고 모든 input과 이었다는 것이고, 로짓회귀와 다르게 모든 항을 반복해서 여러층으로 비선형적으로 이어서 복잡한 함수를 구성했다는 것이다. 또, MLE등의 방법이 불가하니 최적해를 보장할 수 없다는 점도 있겠다.
3-1. 행렬 계산
대부분 인공지능 연산은 행렬을 통해 이루어진다.
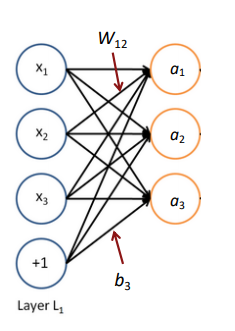
위와 같은 모델은 x 벡터를 a벡터로 맵핑하는 함수라고 할 수 있고, 이를 행렬로 표현해보자면 x벡터를 a 벡터로 사상(project)하는 것이다.
이고,
로 표현할 수 있다.
DNN의 핵심은 비선형성이다. 활성화함수 가 시그모이드 함수 등 비선형 함수이기 때문에, 레이어가 깊어질 수록 함수가 복잡해진다. 만약 선형적이라면 로 단순한 함수로 표현이 가능하기 때문에 사상이 복잡해지지 않아 의미가 없다.
그리고 이것이 가능한 것은, 역전파 덕분이다. 전혀 통계적으로 검정되지 않은 모델이지만(사실 복잡한 수식으로 단순한 모델들이 증명되었다고는 한다), 그럼에도 역전파를 통해 지속적으로 파라미터가 데이터에 적합되면서 모델이 작동하는 것이다.
4. NER(Named Entity Recognition)
NER은 개체명 인식으로 가장 기본적인 자연어처리 태스크 중 하나이다.
"일본 정부의 후쿠시마 오염수 방류 결정으로 한일 갈등이 재점화한 가운데 우리 정부의 개입 요청에 미국 정부가 난색을 보이고 있습니다."
위와 같은 문장에서
일본 정부가 조직이고, 미국 정부 역시 조직이라는 것을 인식하게 하는 태스크이다. 즉, 각 단어가 단체, 인명, 시간, 장소 등의 단어 중 어떤 것을 지칭하는 지 판단하는 태스크이다. 이때 BIO 인코딩을 사용하는데, 각 단어의 이름과 Begin, Inside, Outside 여부를 판단하는 것이다. B는 각 단어의 시작임을 의미하고, I는 각 단어의 일부임을, O는 어떠한 개체에도 속하지 않음을 의미하지 않는다.

NER이 어려운 점은 동일한 단어도 인명일 수도, 지명일수도, 조직일수도 있다는 점이다. 광개토대왕릉비라는 단어에서 광개토대왕은 인물이지만, 광개통대왕릉비는 그렇지 않다. 이러한 단어의 모호성을 어떻게 해소할 수 있을까?
자연어처리에서 거의 항상 그렇듯이, 맥락을 봐야한다. 모델이 하나의 단어를 인식할 때 주변의 단어를 맥락으로 사용하는 것이다. 아래의 예시를 보자.
the museums in Paris are amazing to ~~
이라는 문장이 있을 때 Paris를 객체명 인식하기 위해 문맥 벡터는 주변 2단어의 벡터를 포함하는 벡터가 된다.
그러므로 이 모델의 입력값은 5d 차원이 된다. 이를 DNN에 통과 시킨다.
최종적으로 나오는 s는 Paris가 장소 ner 여부를 판단하게 된다.
단순히 5d 차원의 입력값을 로짓 함수에 통과시킨 것보다 복잡한 함수를 통해, NER이라는 비교적 복잡한 태스크를 수행할 수 있게 된 것이다.
5. 그래디언트 행렬 연산
지금까지 공부하면서 그래디언트를 스칼라 연산으로만 했었다. 미분을 나중에 공부해서 이런 대참사가 일어났는데, 강의에서 마침 행렬 연산을 간략하게나마 하고 있어서 남겨본다.


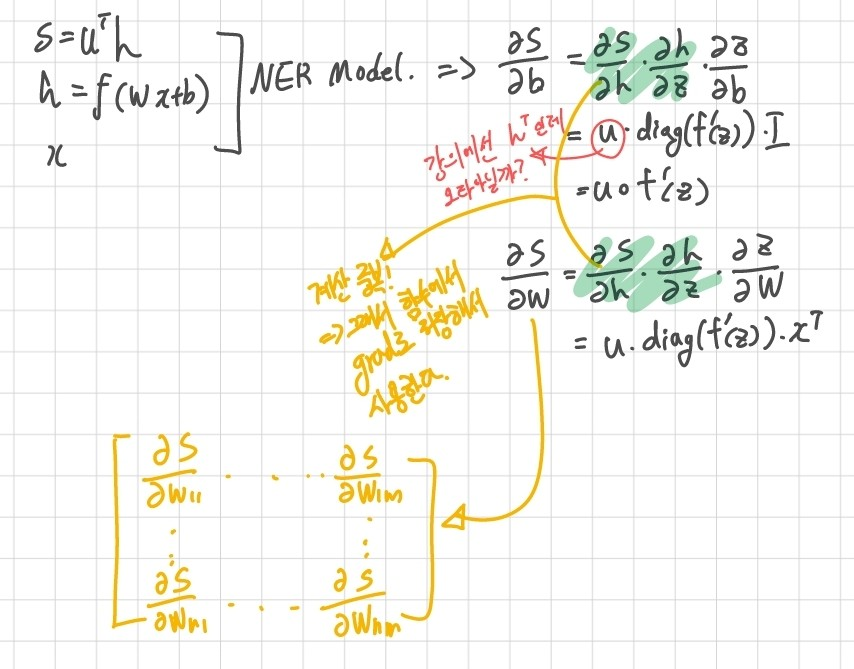
참고
https://wikidocs.net/24682
https://tensorflow.blog/%EB%A8%B8%EC%8B%A0-%EB%9F%AC%EB%8B%9D%EC%9D%98-%EB%AA%A8%EB%8D%B8-%ED%8F%89%EA%B0%80%EC%99%80-%EB%AA%A8%EB%8D%B8-%EC%84%A0%ED%83%9D-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%84%A0%ED%83%9D-1/