이번 강의에선 역전파 과정을 하나씩 살펴본다.

0. 기본적인 역전파

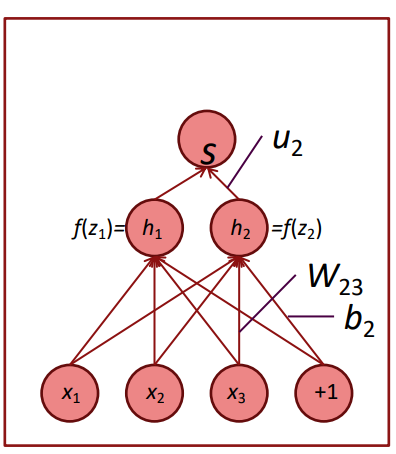
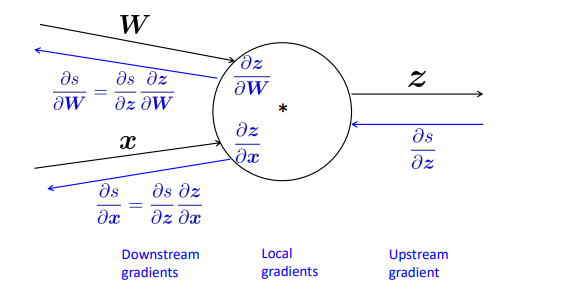
위와 같은 모델에서 W에 대한 편미분은 다음과 같이 진행된다.

${\partial z_i \over \partial W_{ij}}= {\partial \over \partial W_{ij}}(W_ix + b_i)$
${\partial \over \partial W_{ij}}(W_ix + b_i) = {\partial \over \partial w_{ij}} \sum_{k = 1}^dW_{ik}x_k = x_j$

밑의 식에서 가운데 항을 보면, 결국 $W_{ij}$와만 편미분이 이루어진다. 결국 미분한 결과는 $x_j$가 된다.

그리고 역전파의 시작부터 식을 써보면

${\partial s \over \partial W_{ij}} = {\partial s \over \partial h_2} {\partial h_2 \over \partial z} {\partial z \over \partial W_{ij}}$

이런 식으로 체인룰이 적용된다. 이때, 이전의 레이어에서 온 그래디언트인 ${\partial s \over \partial W_{ij}} = {\partial s \over \partial h_2} {\partial h_2 \over \partial z}$를 $\delta$로 치환하면, $W$의 그래디언트 계산은 이전 층의 그래디언트 x 입력값으로 바뀌게 된다. 결국 이 과정의 반복인 것이다. 행렬로 살펴보자면

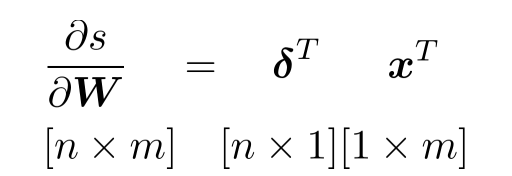
이런 식으로 더 간단하게 표현할 수 있을 것이다.

1. 입력값 in NLP

NLP의 입력값은 기본적으로 자연어라는 점에서 categorical 변수이다. 즉, train에 없던 단어가 test에서 등장하는 경우가 매우 많다. 하지만, 단어 임베딩은 train 과정에서만 학습되고, 이로인해 비슷한 뜻을 가진 단어라도 train에서 등장하지 않은 단어라면 임베딩 공간에서 서로 멀어질 가능성이 높다.

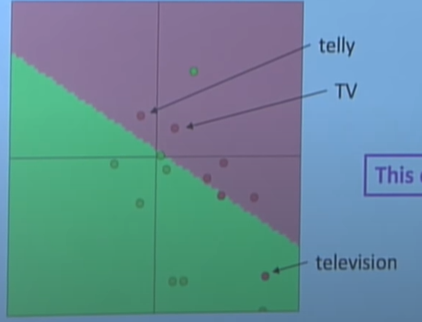
위 사진에서 televsion은 test 데이터에만 존재한다. 이로인해 telly나 TV와 매우 의미가 비슷한 단어임에도 멀리 떨어져 있는 것을 알 수 있다. 이를 어떻게 해결할 수 있을까?

1-1. pretrained word vector

사전학습된 단어 임베딩을 사용하면 이를 해결할 수 있다. 사전학습된 단어 임베딩을 사용하면 몇가지 이점이 있다.

• train에 없는 단어에도 어느정도는 대응이 가능하다. 사전학습된 단어 임베딩은 매우 큰 보캡을 가지고 있다. 보통 우리가 사용하는 데이터를 전부 커버하고도 남을 정도로 많은 단어를 포함한다. 그러므로 앞에서 언급한 out of vocabulary 문제가 발생할 염려가 적다.
• 쉽게 임베딩을 학습할 수 있다. 사전 학습된 모델 구조(word2vec)은 보통 비지도 학습 구조를 가지고 있다. 즉, label이 없는 데이터여도 임베딩 벡터를 학습할 수 있다. 이는 우리의 데이터가 label이 없거나, 그 질이 의심될 때, 손쉽게 회피할 수 있는 방법일 것이다.

여기에 덧붙여서, fine tunning은 해야할까? 강의에선 데이터가 작다면 fine tunning 마저 하지 말라고 한다.

또한, 만약 데이터가 1억 건이 넘는다면 아예 새로 임베딩 레이어를 구성하는 것을 추천하시는 것 같다. 데이터가 많은만큼 파라미터의 수가 많아도 어느저도 강건한 모습을 보이거나, 잘 학습되기 때문일 것 같다.

3. Again, Backpropagation

다시 역전파 이야기로 돌아가면, 2, 3강에서 나온 이야기가 사실 거의 전부이다. 다른 점이 있다면, 역전파하면서 이전 계층의 그래디언트를 저장하면서 계속 사용한다는 점이 있을 것이다.

이전에 계속 봐온 모델을 다시 예시로 삼아보자.
$s = u^Th\\h = f(z)\\z = Wx + b \\x$

순전파의 경우 위와 같이 진행될 것이다. 그리고 거꾸로 진행되는 역전파는 체인룰에 의해 아래 그림과 같이 정리할 수 있다.

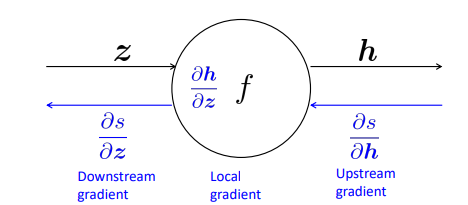
3-1. backpropagation in dot product

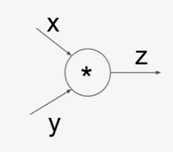
두 항의 곱으로 연결된 노드의 경우 어떻게 미분할 수 있을까? 사실 스칼라 미분 계산을 해보면 매우 쉽게 나오는데, 정답은 다음 그림과 같다.

사실 여기엔 나오지 않았는데 이 결과는 ${\partial s \over \partial W} =\delta*x$와 같다. x의 경우엔 $\delta*W$가 된다. 즉, 서로 반대의 입력값을 그래디언트에 곱하면 자신의 그래디언트가 된다.

3-2 backpropagation in plus and max node

덧셈과 맥스 노드에선 어떻게 될까? 이 역시 어렵진 않다. 다음 그림과 같은 구조를 생각해보자.
$a = x + y \\ b = max(y, z) \\ f = ab$

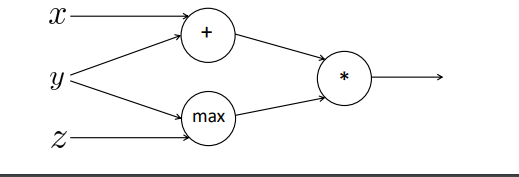
• 덧셈 노드
  x와 y는 덧셈 노드로 연결되어 있고, y와 z는 max 노드로 연결되어 있다. 곱셈 노드가 서로의 입력값을 바꿔서 그래디언트를 전달했다면, 덧셈 노드는 그저 정확히 분배하면 그만이다.
  ${\partial f \over \partial x} = {\partial f \over \partial a}{\partial a \over \partial x}$가 된다. 그러므로
  ${\partial f \over \partial a} * 1$가 된다 즉, 그래디언트가 그대로 전달될 따름이다. 동일한 그래디언트가 x와 y로 흘러간다. 다만, 각 항에 따른 미분값이 곱해지겠다.

• max 노드
  max 함수는 다음과 같다.

$max(y, z) = z\quad if\quad z>y \quad else \quad y$

${\partial f \over \partial z} = {\partial f \over \partial b}{\partial b \over \partial z}$

${\partial f \over \partial b}{\partial b \over \partial z} = a*{\partial z \over \partial z }\quad if \quad z >y$

${\partial f \over \partial b}{\partial b \over \partial z} = a*{\partial y \over \partial z }\quad if \quad z < y$

즉, max 노드와 이어져 있는 두 값중 큰 값으로만 그래디언트가 흘러가게 된다.

3-3. forward / backward propagation

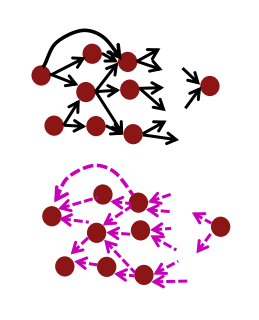
위 그림은 순전파와 역전파를 나타낸 것이다. 한번도 생각해보지 못한 것인데, 역전파와 순전파의 big O notation은 같다. 왜냐하면 순전파는 그래프를 따라서 수가 흘러가는 것이고, 역전파 역시 반대 방향으로 그래프를 따라서 수가 흘러가기 때문이다. 그러므로 두 과정은 모두 시간복잡도가 거의 정확히 같을 수 밖에 없다(BM등이 끼어들면 정확히 같지는 않을 것 같다).

class ComputationalGraph(object):
	(1) 생략된 코드1 : input data 받기
	def forward(inputs):
    	 for gate in self.graph.nodes_topologically_sorted():
         	gate.forward()
         return loss
    def backward():
    	for gate in reversed(self.graph.nodes_topologically_sorted()):
        	gate.backward()
        return inputs_gradients

텐서플로우는 모르겠지만, 파이토치나 스크래치로 DNN을 구현하면 위와 같은 플로우를 따르게 된다. 각각의 레이어가 하나의 객체가 되고, forward 메소드에선 레이어가 input부터 순서대로 순전파되게 된다. 이후 backward 메소드에선 레이어를 역순으로 돌려 각 레이어의 backward 메소드를 수행하는데, 이때, 이전 레이어의 그래디언트를 받아서 순전파 시 입력값과 연산을 통해 해당 레이어의 그래디언트를 계산하게 된다.

위와 같은 노드는 다음과 같이 구현할 수 있다.

class MultiplyGate(object):
	def forward(x, y):
    	z = x*y
        self.x = x
        self.y = y
        return z
    def backward(dz):
    	dx = self.y*dz
        dy = self.x*dz
        return [dx, dy]

forward 메소드를 보면, 굳이 x와 y를 클래스 어트리뷰트로 선언하는 것을 볼 수 있는데, 곱셈 노드는 체인룰에서 입력값*그래디언트가 해당 레이어의 그래디언트이기 때문이다. 즉, forward에서 선언한 x와 y를 backward에서 사용하는 것을 볼 수 있다.

3-4. old gradient checking

크게 중요하진 않지만, 조금 재밌던 이야기를 적어보자면, 2014년 이전의 연구자들은 모든 그래딩언트를 직접 손으로 계산해봤다고 한다... (왜 컴퓨터를 못 믿지? 코딩을 제대로 했다면 굳이...?)

4. 기타 논의점

4-1. Regularization

손실 함수에 대해 이야기하다 보면 종종 예측값이나 실제값과 상관없는 항을 볼 때가 있다.

$J(\theta) = {1 \over N}\sum^N_{i = 1}-log({e^{f_{ui}} \over sum^C_{c = 1} e^{f_c}}) + \lambda \sum_k\theta^2_k$

위 식에서 앞의 부분은 평범한 negative log liklihood처럼 보인다. 하지만 뒤에 람다와 파라미터는 왜 나타날까? 이는 모델의 오버피팅과 관련이 있다. 훈련 데이터는 우리가 원하는 문제를 정의하는 모든 데이터가 아니다. 항상 샘플링되어 편향되어 있다. 이를 고려하여 모델은 훈련 데이터를 적합하되, 어느 수준이상으로 적합하면 안된다. 과도하게 훈련 데이터에 적합되면, 다른 데이터(테스트 데이터)에 제대로 성능을 내지 못하게 된다.
그리고 파라미터가 0에서 멀어질수록 데이터에 적합되게 된다. 그러므로, 모델이 학습데이터에 과도하게 적합되지 못하도록 크기를 조절해줄 필요가 있다. 위 식의 뒷 항이 바로 l2 norm을 이용하여 파라미터의 크기를 제한하는 panelty term이다.

4-2. Vectorization

R에서 파이썬으로 넘어오면서 좋았던 것 중 하나가 맘껏 for loop을 쓸 수 있는 것이었다. 자세한 이유는 모르지만, R은 for loop이 늘어갈 수록 정말 급격하게 느려진다. 하지만 파이썬은 비교적 이러한 속도 저하에서 자유로워서 4중 loop 정도는 이제 맘놓고 쓴다. 그래도 느릴 때가 분명히 존재한다. 그래서 속도를 빠르게 하는 방법은
for loop -> list comprehension -> vectorization이라고 알고 있다. 이 점을 유념하면 좋을게, 굳이 더 빠른 방법을 쓸 수 있는 경우인데, 느린 방법을 사용할 필요는 없다. 특히 모델 연산은 행렬로 이루어진다는 점에서 vectorization은 선택이 아닌 필수다.

4-3. Non-linearity

Sigmoid, Tanh, ReLU 등 딥러닝 모델의 활성화 함수는 무조건 무조건 무조건 별다른 이유가 없다면 비선형함수를 사용한다. 함수들을 하나씩 살펴보자.

4-3-1. Sigmoid

$f(z) = {1 \over 1+exp(-z)}$

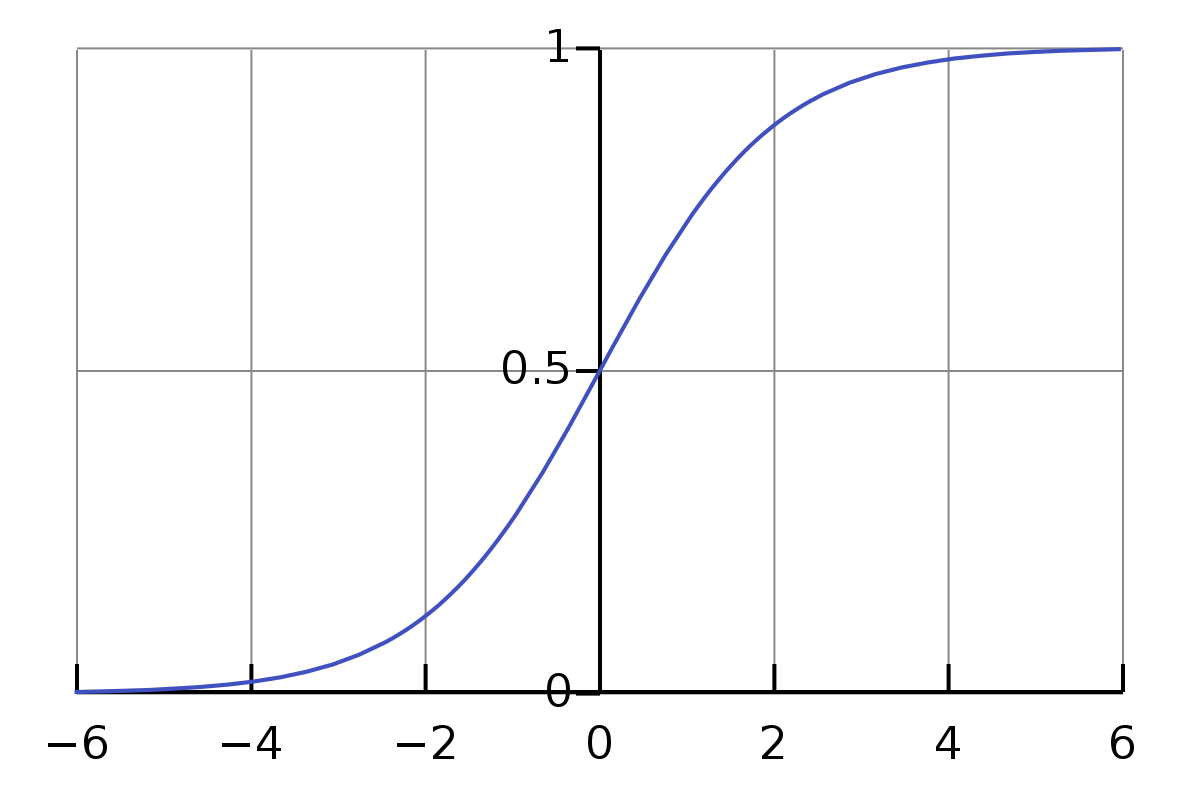
시그모이드 함수는 로지스틱 회귀에서 사용되던 함수다. 함수 자체로 확률을 내뱉어준다는 점에서 매우 간편하다. 하지만 함수의 중심이 0이 아닌 0.5이기 때문에 활성화 함수가 겹겹이 쌓여있는 구조의 DNN 이상의 모델에선 편향된 출력값이 나오는 경향이 있다.

4-3-2. Tanh

$f(z) = {e^z -e^{-z} \over e^z + e^{-z}}$

하이퍼볼릭 탄젠트 함수는 시그모이드 함수를 일부 변형했다. y의 범위를 -1 ~ 1로 조정하여 함수의 중심이 0이 되도록 한 것이다. 이를 통해 모델을 깊이 쌓는데 조금이나마 도움이 되었다고 한다. 하지만 이 함수의 문제는 연산량이 증가했다. 지수함수가 네개나 사용되었기 때문이다.

4-3-3. hard tanh

나중에 식 삽입하기

그래서 나온게 hard tanh이다. 대략적인 하이퍼볼릭 탄젠트 함수의 모양을 따르면서도, 연산량은 획기적으로 줄었다. 이때 x가 -1 ~ 1일 경우 기울기가 1인 선형성을 보이는데, 딥러닝 분야에서 이는 크게 중요하지 않았다고 한다. 어쨋든 잘 작동하기 때문이다. 이유는 아마 역시 미분이 0 또는 1이기 때문에 역전파가 잘 전달되기 때문일 것이다(뇌피셜입니다.).

4-3-4. ReLU(Tectified Linear Unit)

hard tanh이 잘된다면, 더 단순화시켜보자는 아이디어에서 나왔다고 한다. 현재 정말 디폴트로 사용하는 함수다. 단순한 모양이 엄청난 성능을 보이는게 항상 신기할 따름이다. 빠르고 성능이 좋다니 완벽하지 아니한가.

4-4. Parameter Initialization

지금까지 이야기한 내용 중 사실 가장 근원적인 질문은 해소되지 않았다. 그렇다면, 초기의 모델은 어떤 값을 가져야 하는가? 교수님께서 강의하시면서 파라미터의 초기화는 "vital"하다고 한 10번쯤 강조해서 말씀하신다. 실제로, 내가 코드 실수로 모든 파라미터를 0으로 놓고 학습을 시킨 적이 있었는데, 거의 학습이 되지 않거나, 매우 느리게 되는 모습을 보였다.
모든 파라미터를 0으로 놓고 학습시킬 경우, 파라미터들은 비슷하게 업데이트 되어버린다. $\theta_{new} = \theta_{old} - \lambda * gradient$인데, $\theta_{old}$가 모두 같고, gradient가 흘러온 과정도 모두 같으니 같은 층의 노드와 파라미터들은 동일한 gradient를 가질 수 밖에 없어진다. 이러면 모델을 깊게 쌓은 이유가 사라져버린다.

파이토치나 케라스 등의 모듈에선 초기화 방법을 여러 개 제공하는데, 여기서 핵심은 activation function을 통과하면서 gradient descent나 explode가 발생하지 않도록 하려는 것이다.

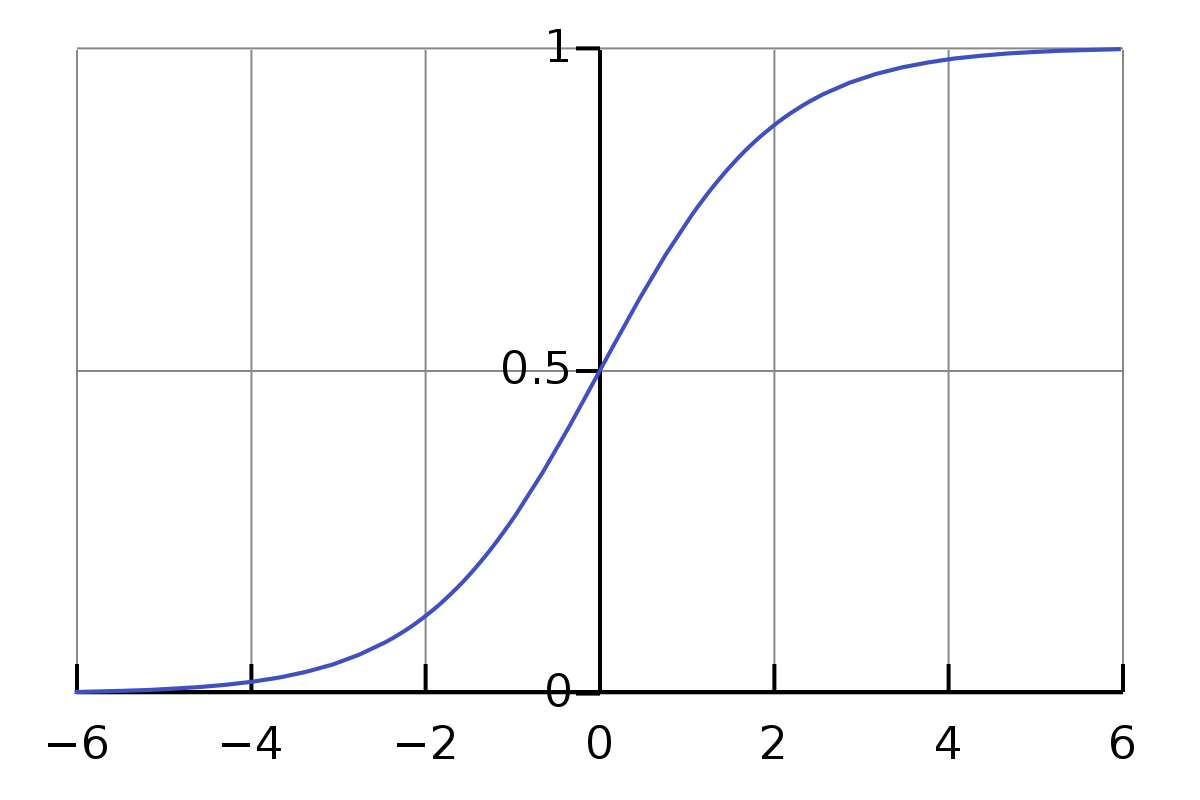
시그모이드 함수는 0에서 가까운 범위에서 기울기(gradient)가 의미있는 정도의 값을 가진다. 만약 x의 절대값이 너무 커지면, gradient는 작아지고, 학습이 제대로 이루어지지 않게 된다. 그러므로 x 혹은 y(이전 층의 y는 이번 층의 x이다)는 0 근처의 값으로 초기화되는 것이 좋다.

가장 유명한 초기화 방법은 Xavier initilization으로 다음과 같다.
$Var(W_i) = {2 \over {n_{in} + n_{out}}}$

여기서 분모의 값은 파라미터의 입력에 위치한 노드의 개수와 출력에 위치한 노드의 개수이다. 입력과 출력에 노드가 많을 수록 결국 z 값은 커지기 마련이기 때문에, 두 노드의 개수에 따라 파라미터 초기값을 작게 유지하려고 하는 것이다.

4-5. Optimizer & Learning Rate

옵티마이저에 대한 내용은 나중에 시간이 된다면 하나씩 수식과 함께 설명하고 싶다. 강의에선 대략적인 개념만 말하고 넘어간다.

LR은 기본적으로 0.0001과 같은 작은 상수를 사용한다. 하지만 모델은 학습하면서 점차 수렴해가기 때문에, 점점 작은 lr을 필요로 하게 된다. 이는 스케줄러를 통해 조절할 수 있는데, 단순히 k번째 에포크마다 1/2을 할 수도 있고, 다른 식을 통해 조절할 수도 있다.