KPMG Future Academy AI 활용 데이터 분석가 3기 40일차 수업을 2025년 1월 14일에 참석했다.
- 데이터 수집
1.1. 웹 크롤링, 스크래핑
1. 데이터 수집
1.1. 웹 크롤링, 스크래핑
URL (URI : Uniform Resource Identifer 중에서 위치정보를 포함한 식별자)

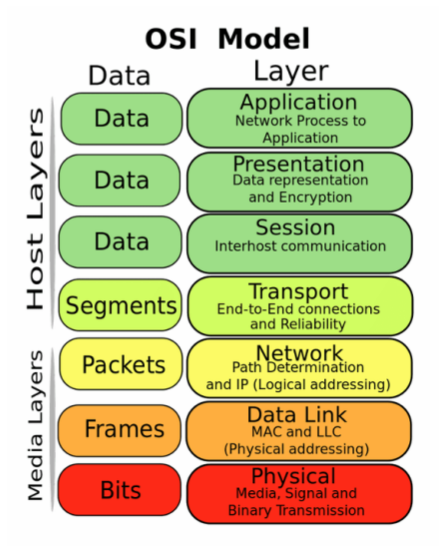
OSI 7 Layer : 국제표준화기구(ISO)에서 정의한 네트워크 통신을 7단계로 나눈 참조 모델
쿠키
Client에 저장하는 문자열 데이터. 도메인별로 분리되어 저장.
용도 : 로그인 상태 유지, 팝업 방지 등
하나의 클라이언트에 300개, 도메인당 20개, 쿠키 하나당 4kbyte
세션
서버에 저장하는 객체 데이터. 브라우저와 연결시 session ID 생성
session ID를 쿠키에 저장하므로 로그인 연결 유지
같은 브라우저로 같은 서버에 접속하면 session ID가 같음
용도 : 로그인 상태 유지, 사용자별 데이터 관리
캐시
Client나 서버의 메모리에 저장해서 빠르게 데이터를 가져오는 목적의 저장소
용도 : 자주 사용하는 데이터를 캐시에 저장하여 속도 향상
Client
HTML
CSS - less, sass
Javascript - vue.js, react.js, angelar.js, backborn.js
서버
Python - FAST API, Django, Flask
Java - Spring
Ruby - Rails
Javascript - Node.js (Express)
Scala - Play
HTML Status Code

HTTP Message
라인, 헤더, 바디 영역으로 나뉨. 헤더와 바디 영역은 공백으로 구분.
바디영역을 제외한 나머지 영역(요청, 헤더)의 각 라인은 연속된 CR/LF(\r\n) 문자로 구분.
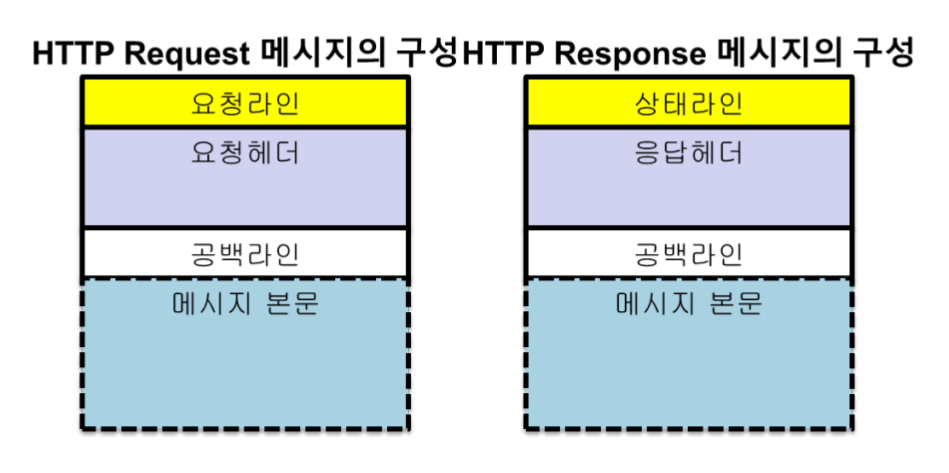
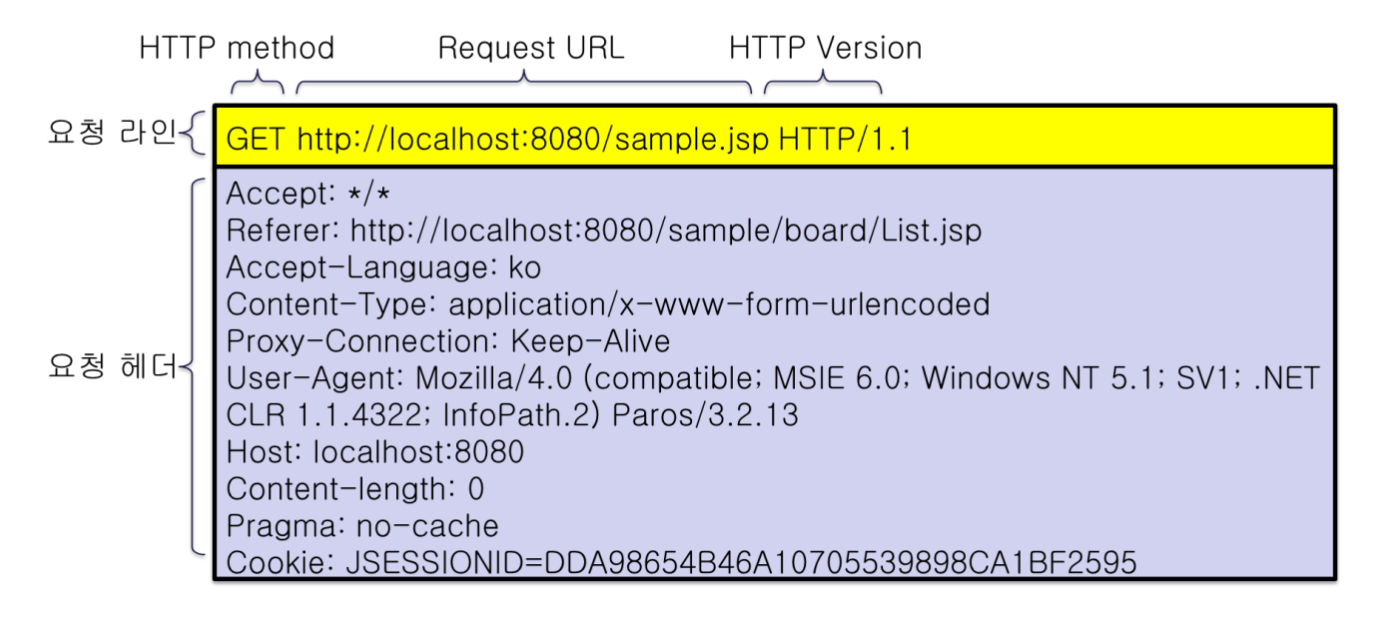
GET Request 메시지
Response 메시지

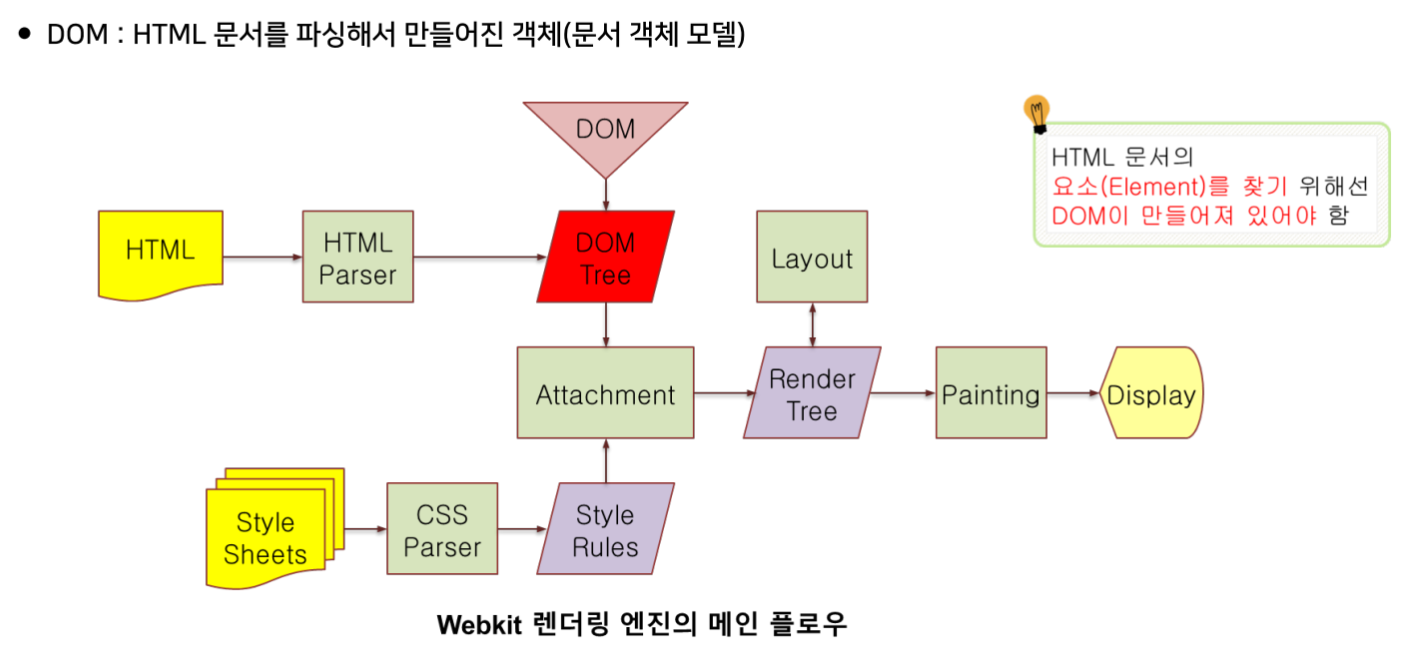
렌더링 엔진
렌더링 엔진 종류
WebKit: Safari에서 사용
Blink: Chrome, Edge, Opera에서 사용
Gecko: Firefox에서 사용
DOM : 문서 객체 모델
https://developer.mozilla.org/ko/docs/Web/API/Document_Object_Model
웹 아키텍처
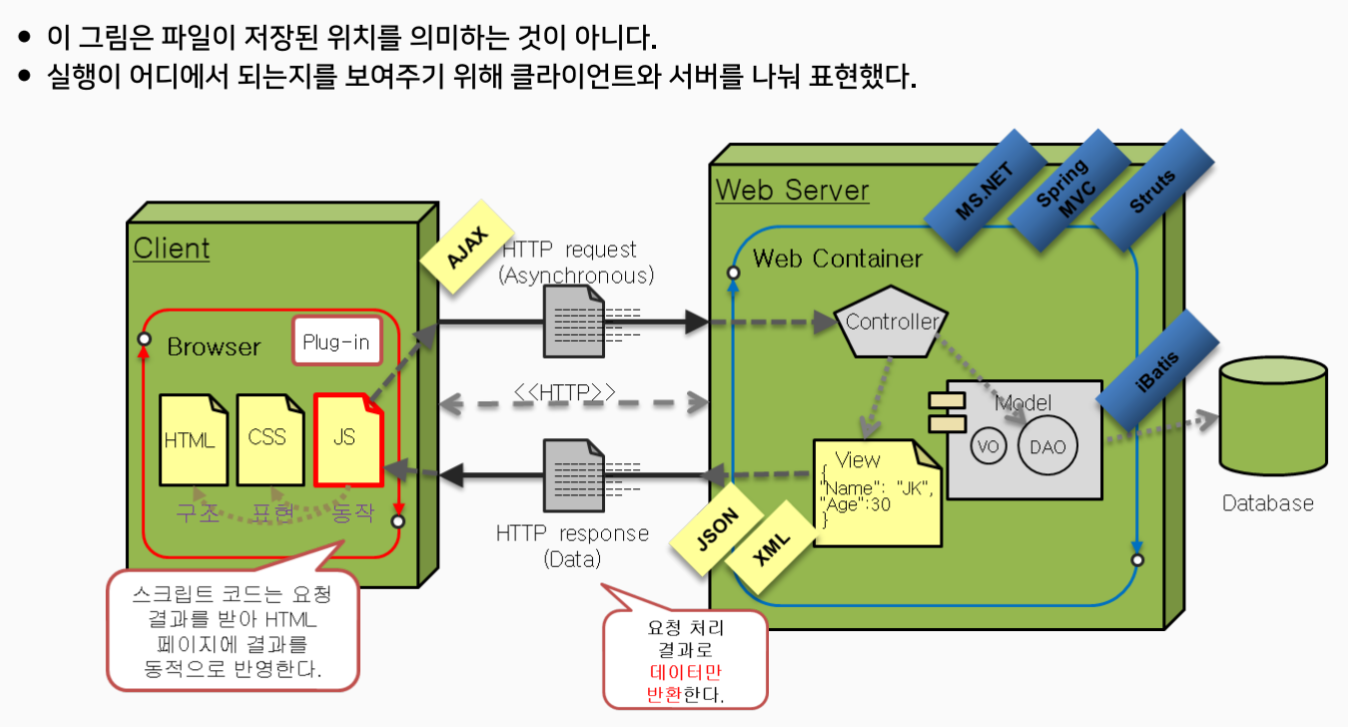
주피터노트북에서 HTML 요소 확인
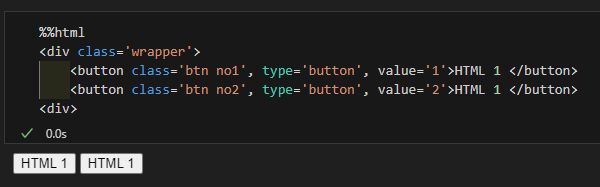
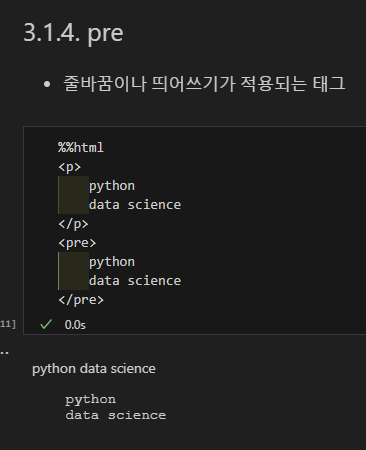
pre 태그
비주얼스튜디오에서 !+탭을 누르면 html 코드가 자동으로 입력됨.
아래 파이썬 모듈로 응답 받아오기
import requests
response = requests.get('http://www.naver.com')
print(response.status_code)
가상환경 터미널에서 아래 코드를 입력하면

응답했다는 200 코드가 뜸 (성공)

BeautifulSoup
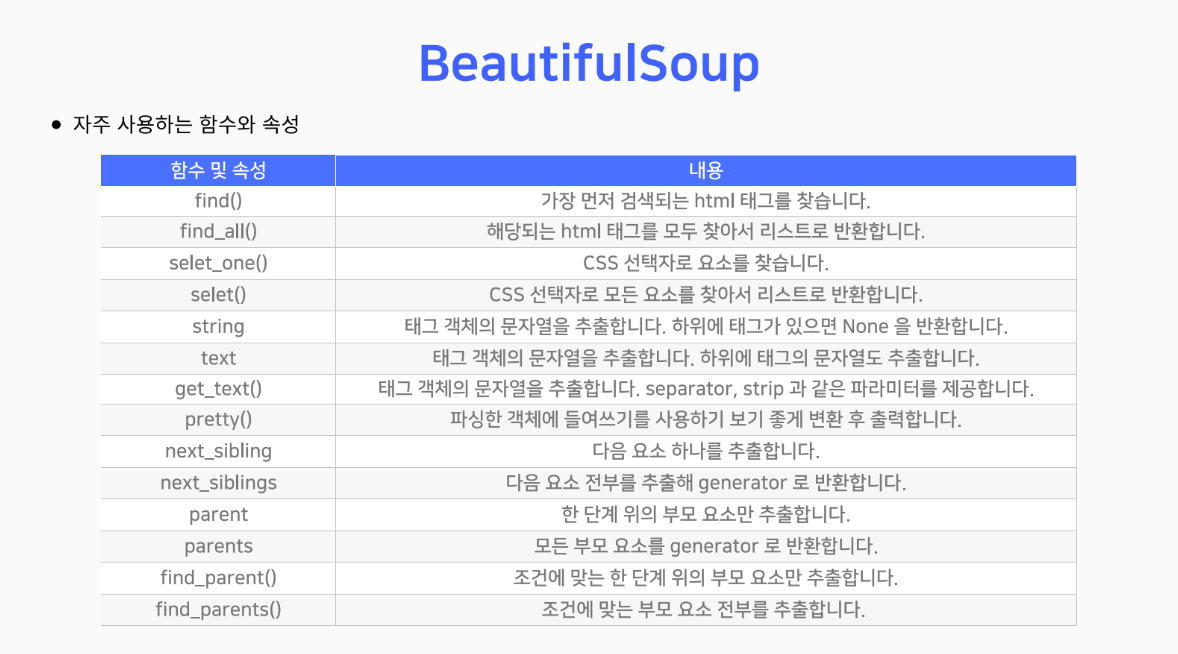
본격적으로 웹 스크래핑 시작
BeautifulSoup 설치
라이브러리 업데이트 등 경고 무시 설정해두기
html 요소 얻기
- 유의할 점 - m.으로 시작하는 모바일 주소로 변환
- response의 status code가 200이 나오는지 확인
- 403이나 500이 나오면 request가 잘못되거나 web server에서 수집이 안 되도록 설정이 된 것
- header 설정 또는 selenium 사용
- 200이 나오더라도 response 안에 있는 내용을 확인 > 확인하는 방법 : response.text
파싱
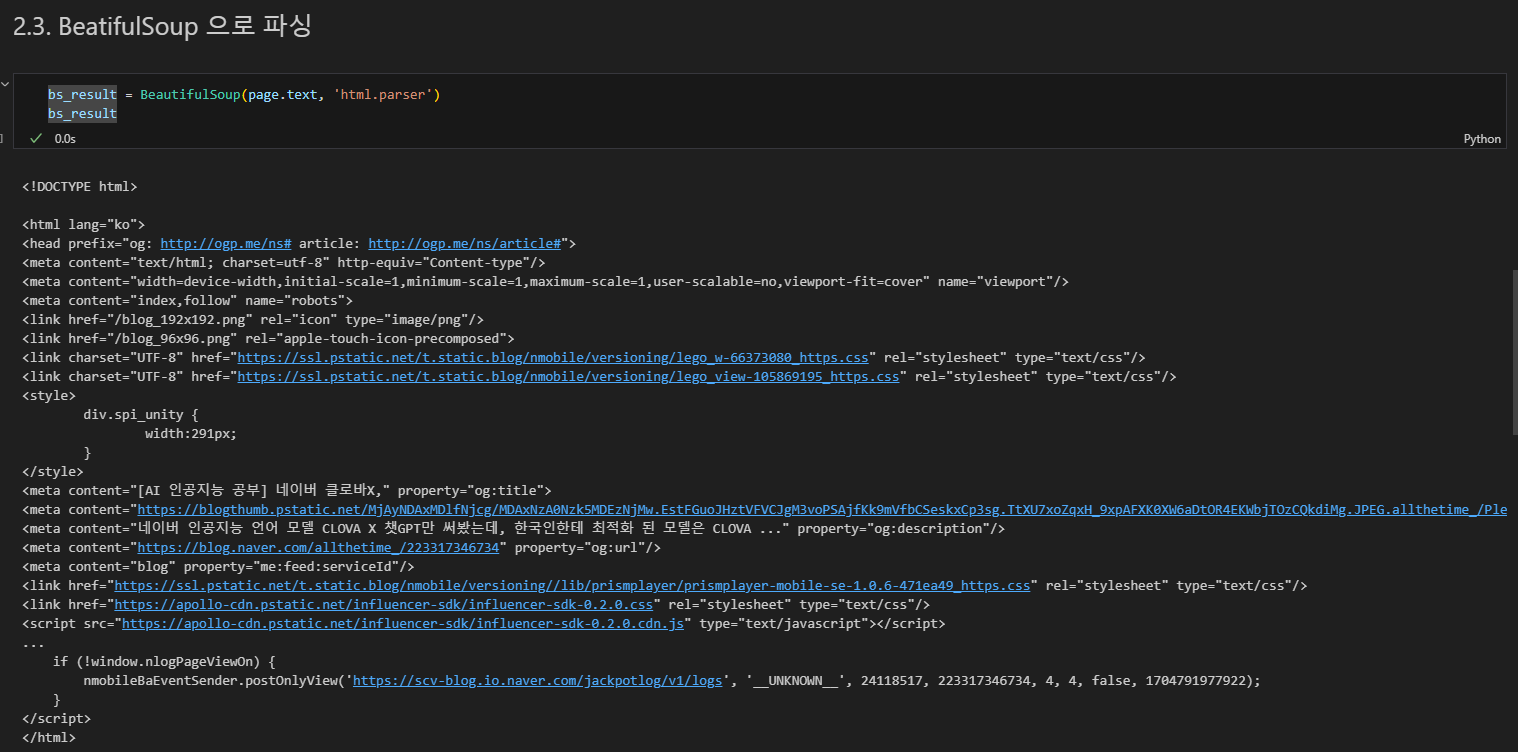
find_all() html 태그를 모두 찾아서 리스트로 반환하는 함수
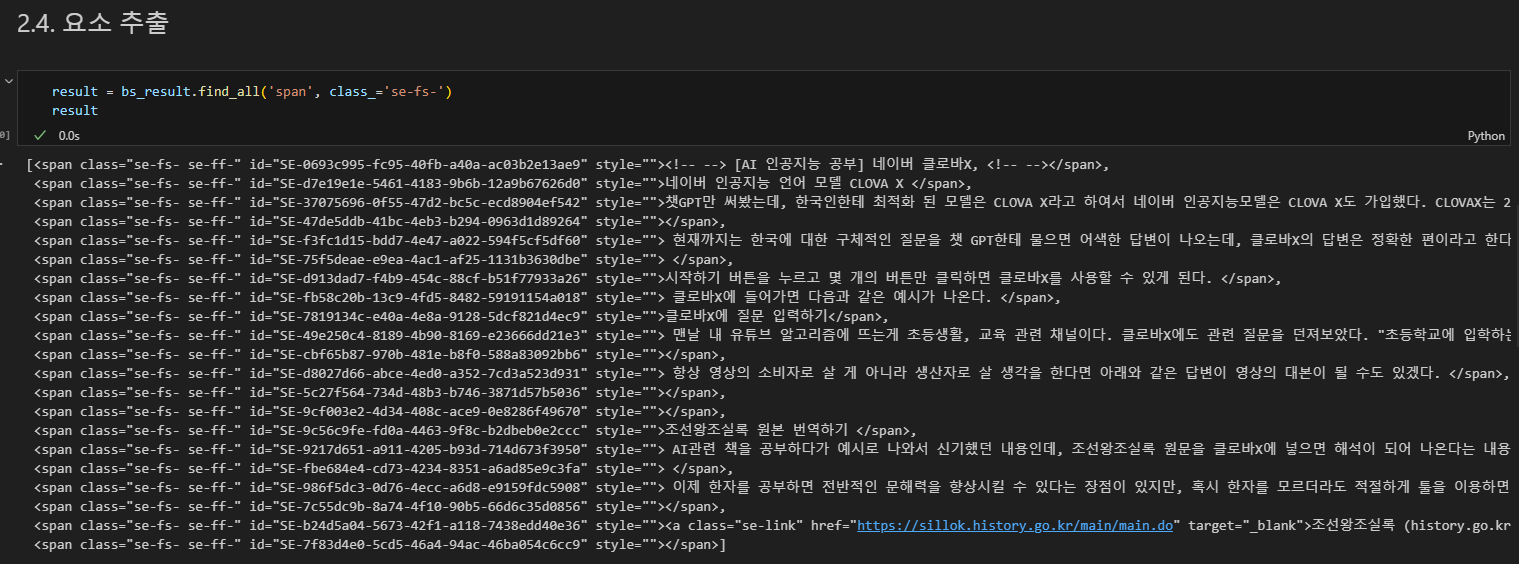
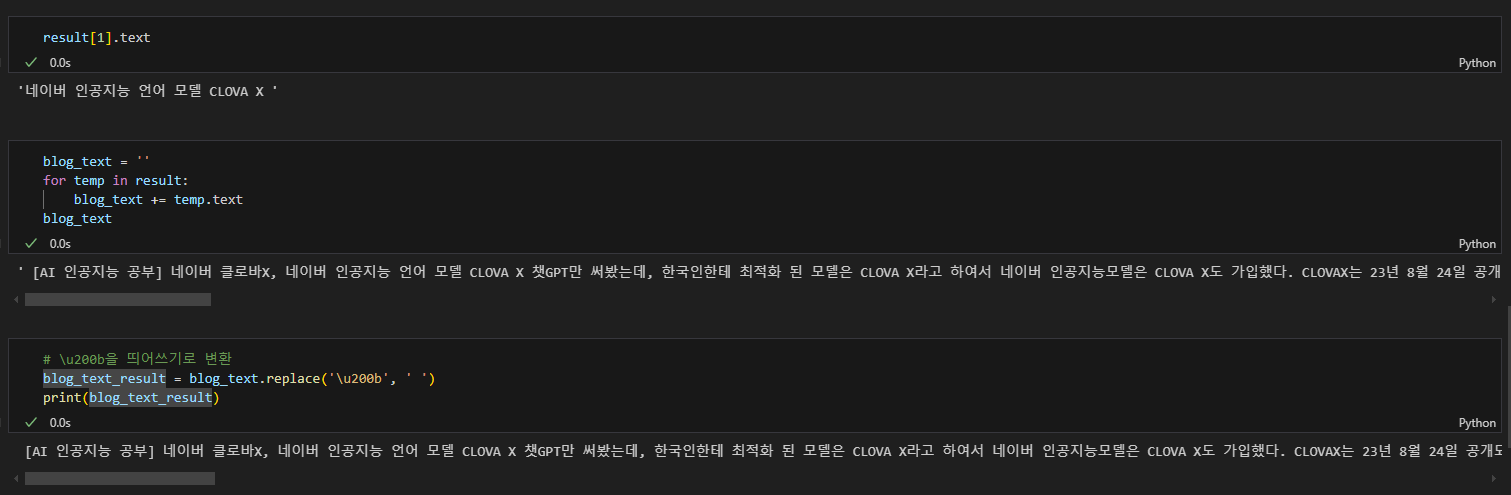
요소 추출
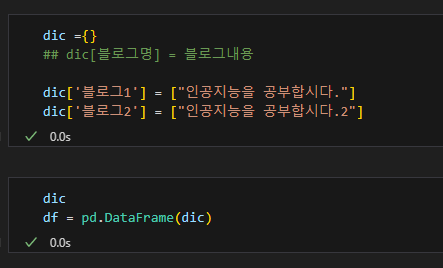
데이터프레임으로 저장
Parser 종류

네이버 날씨 정보 찾기 (두번에 걸쳐서)
keyword 변수에 지역명 반영

파싱
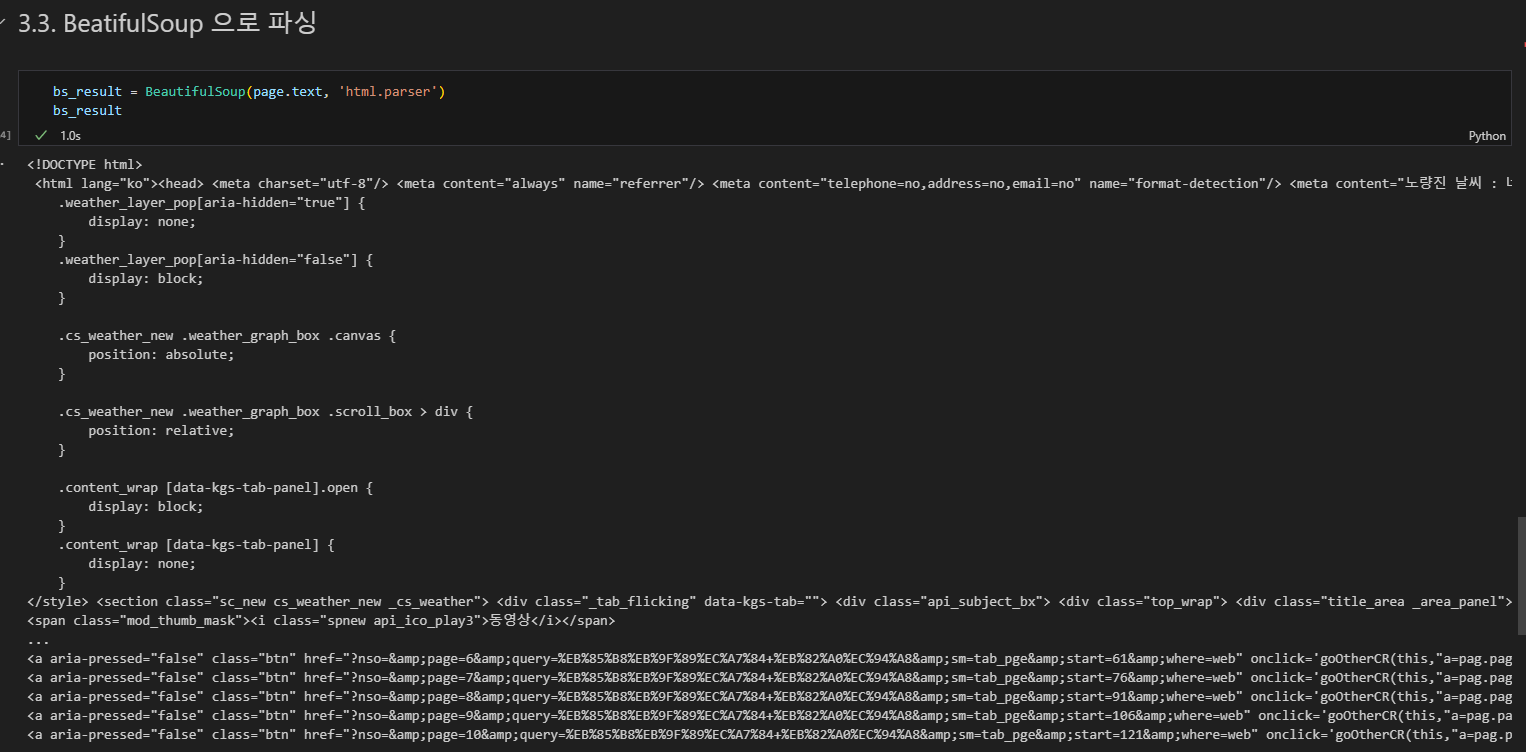
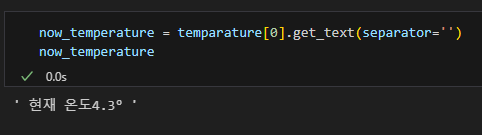
find() 태그별 추출
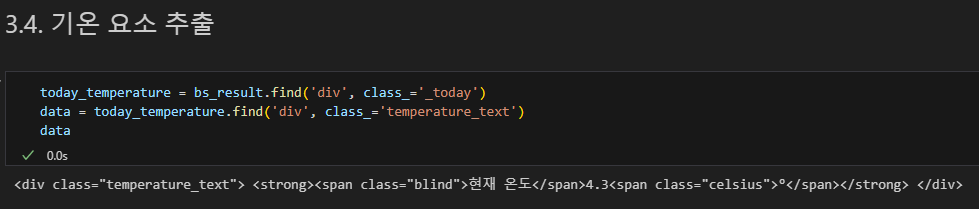
get_text() 텍스트만 추출
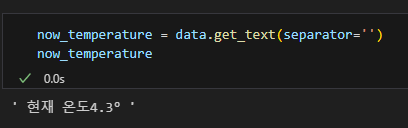
find_all() 한번에 찾기
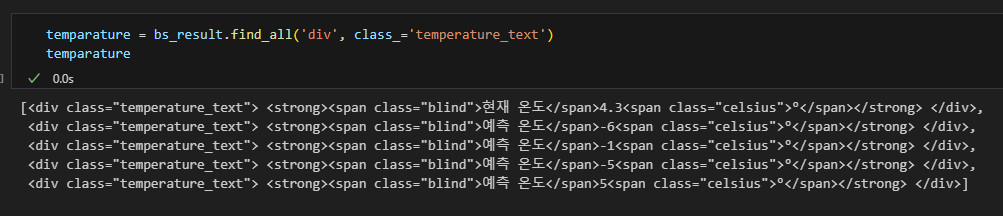
get_text() 텍스트만 추출
copy > selector
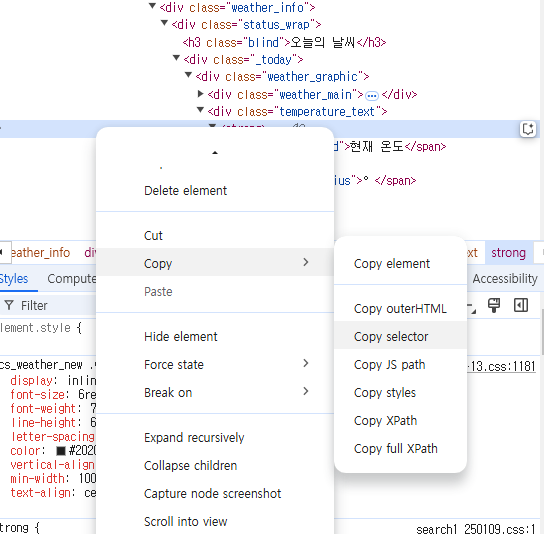


네이버 증권에서 USD 환율 가져오기
https://finance.naver.com/marketindex/?tabSel=exchange#tab_section
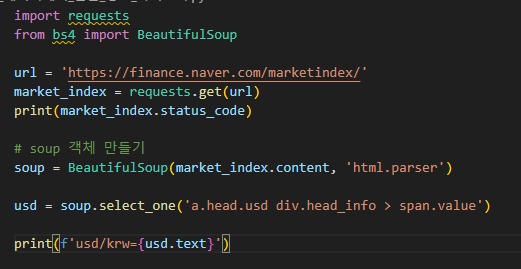
환율 데이터 불러옴

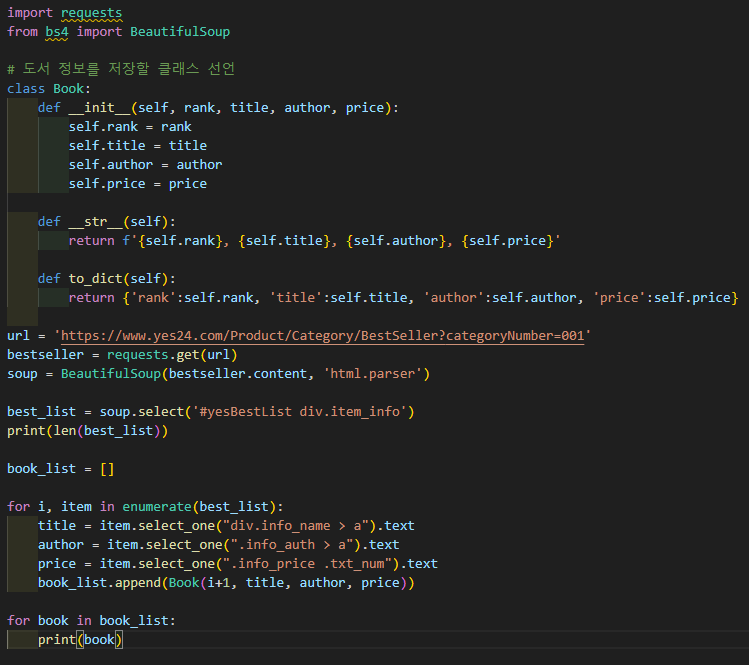
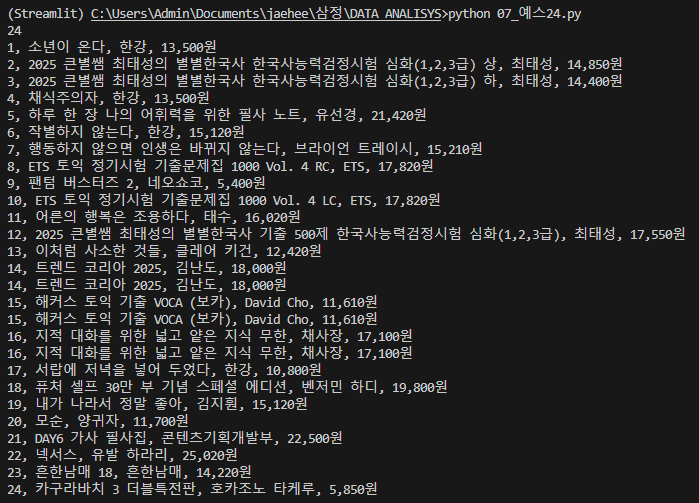
도서 베스트셀러 리스트로 출력하기
멜론차트 100
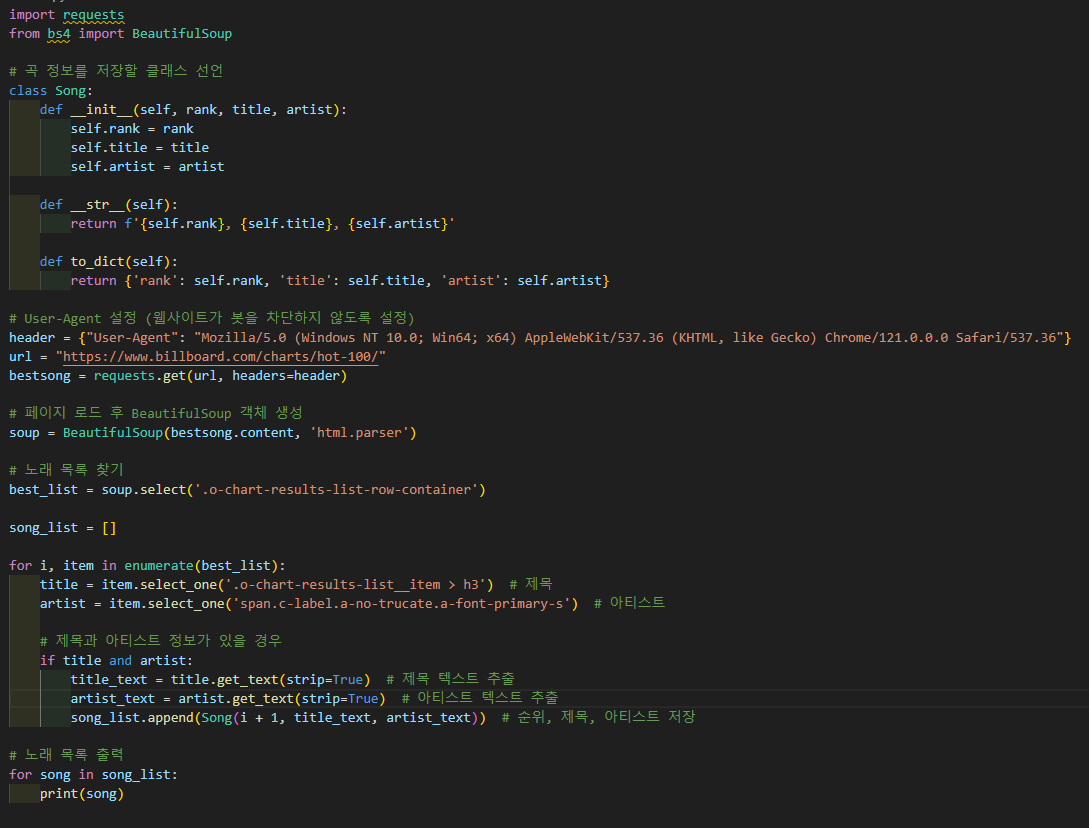
봇 차단 방지 헤더 추가
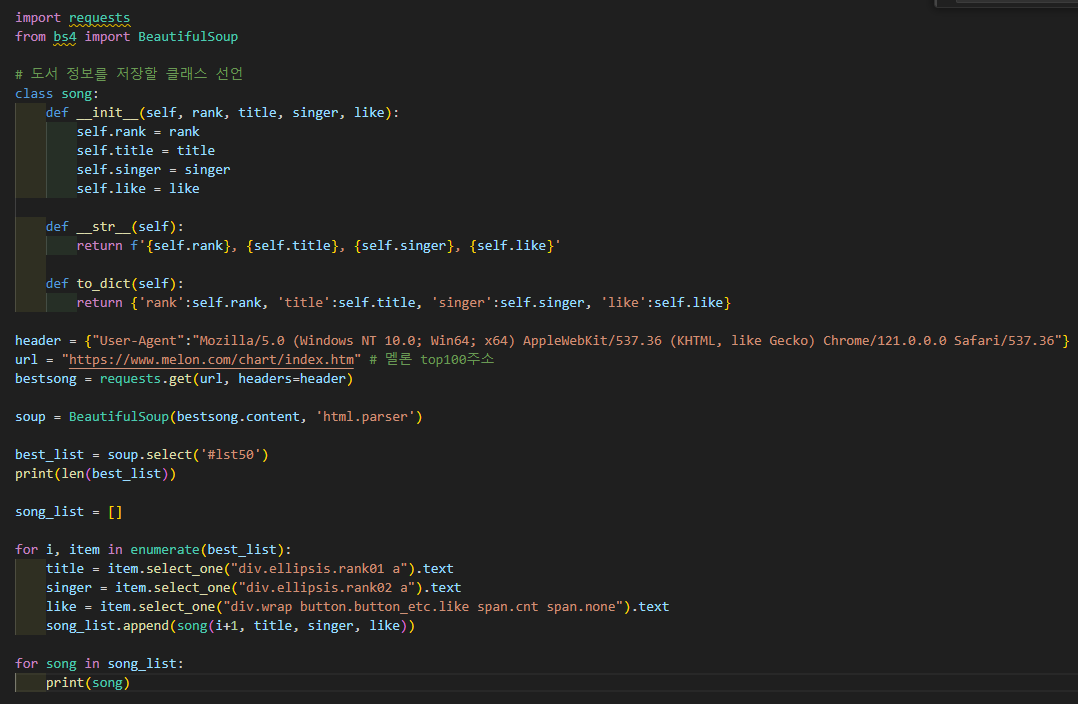
이렇게 했을 때 좋아요 집계 수치가 불러와지지 않았다.
이유 추정
멜론 좋아요수, 네이버증권(시장지표) 표의 필리핀 페소(https://finance.naver.com/marketindex/ 이 경우는 iframe이 원인), 기상청 기온정보 등
안불러와지는 이유 추정 (출처 : Claude)
- 동적 콘텐츠
- JavaScript로 동적으로 데이터가 로드되는 경우
- 페이지 로드 후 AJAX 요청으로 값이 업데이트되는 경우
- BeautifulSoup은 정적 HTML만 파싱할 수 있어서 동적으로 생성되는 콘텐츠는 가져올 수 없음
- 페이지 로딩 보안
- 웹사이트에서 크롤링 방지를 위한 보안 조치가 있을 수 있음 (선생님이 알려주신 봇방지 해제 코드 헤더 추가함)
- User-Agent 헤더가 없거나 차단된 경우
- IP 기반 접근 제한이 있을 수 있음 (이건 아닐듯)
- HTML 구조 변경
- 실시간으로 class나 구조가 변경되는 경우
- A/B 테스트로 다른 버전의 페이지가 로드되는 경우
요즘에는 사이트에서 requests를 막는 경우도 많다고 함.
내일 동기, 비동기 통신을 배우면 더 잘 알 수 있을 듯하다.
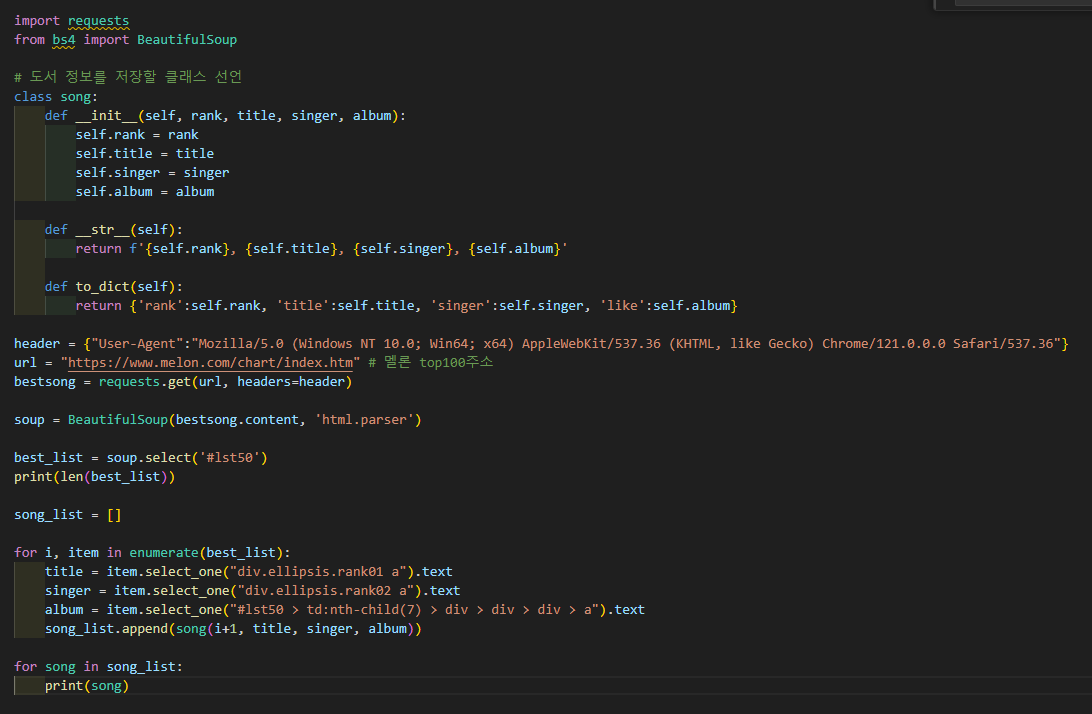
그래서 일단 좋아요수 대신 앨범명으로 대체하여 스크래핑함.
빌보드차트 100
https://www.billboard.com/charts/hot-100/
곡제목 100개에 동일한 id가 적용되어 있는 것을 발견하였음.
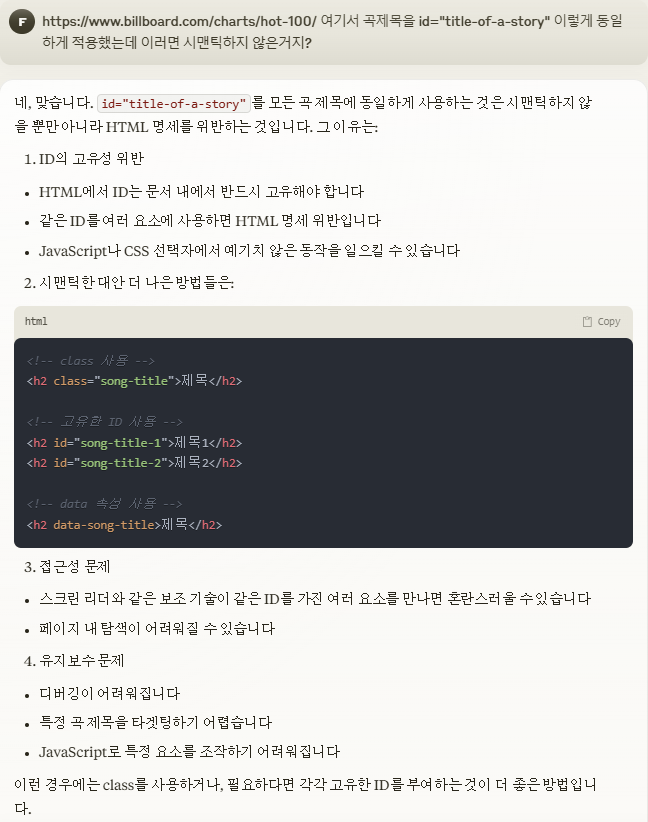
이러면 무려 HTML 명세 위반이라고한다.
야놀자 vs. 여기어때
잡코리아 vs. 사람인
웹 크롤링 소송 문제가 화두가 되었음.
(배상액 산정의 기준이 궁금하다.)
https://www.google.com/robots.txt 등에서 제한사항을 확인 가능.
selenium으로 동적 데이터 불러오기는 내일 배운다. (TBD)
번외
출처 : 빅데이터 시대, 올바른 인사이트를 위한 통계 101×데이터 분석
통계
제1종 오류, 위양성 (false positive) : 실제로는 차이가 없음에도 차이가 있다고 판단하는 오류. (잘못된 귀무가설 기각 및 대립가설 채택), 유의수준 α (제1종 오류가 일어날 확률). 유의수준 α를 미리 정해서 오류가 일어날 확률을 통제함.
a = 0.05란 귀무가설이 옳을 때 평균적으로 20번 중 1번 정도 귀무가설을 착오로 기각하고 대립가설을 채택한다는 뜻.
제2종 오류 : 실제로는 차이가 있는데도 차이가 있다고 말할 수 없어 귀무가설을 기각하지 않는 판단을 내리는 오류. β : 제2종 오류가 일어날 확률. 표본크기 n이 커질수록 작아짐.
검정력(power of test) : 1-β
일반적으로 1-βfmf 80%로 설정. α와 달리 직접 통제할 수 없음.
α와 β는 상충관계.
효과크기(effect size) : 얼마나 큰 효과가 있는지 나타내는 지표. 평균값의 차이에 비해 표준편차가 클수록 2개 분포의 겹치는 부분이 커지므로, 효과크기 d는 작아지고 평균값의 차이는 검출하기 어려워짐. 검출하고 싶은 효과크기를 미리 설정하는 것이 바람직함.
α, β, n, d의 네 값 중 셋을 결정하면 나머지 하나는 자동으로 정해짐.
다양한 검정
모수검정(parametric test) : 모집단이 수학적으로 다룰 수 있는(파라미터로 설명할 수 있는) 특정 분포를 따른다는 가정을 둔 가설검정. 대부분 모집단의 분포가 정규분포인 경우에 해당.
정규성이 없으면 비모수검정. : 좌우 비대칭, 양봉형, 이상값 있음 등.
등분산성 : 분산이 같은 성질.
일표본 t검정 : 귀무가설 - 모집단 평균(μ)은 OO이다. 대립가설 - 모집단 평균(μ)은 OO이 아니다.
웰치의 t검정 : 2개 집단의 분산이 다르더라도 검정 가능. 귀무가설 - 2개 집단의 평균값은 같다. 대립가설 - 2개 집단의 평균값은 다르다.
정규성 조사
Q-Q 플롯
샤피로-윌크 감정
콜모고로프-스미르노프(K-S) 검정
비모수 검정 : 데이터에 정규성이 없을 때.
1. Mann-Whitney U 검정 (두 독립된 집단 비교) : 두 독립적인 집단 간에 중앙값 차이를 비교하는 검정. 정규성 가정 없이 두 집단의 차이를 검정할 때 사용.
사용 예시: 두 집단의 평균 차이가 아니라 순위 차이를 비교하려는 경우.
2. Wilcoxon 부호 순위 검정 (두 관련된 집단 비교) : 두 관련된 집단 간에 차이를 비교하는 비모수 검정. 쌍을 이루는 두 집단의 차이가 정규분포를 따르지 않을 때 사용.
사용 예시: 같은 집단에서 두 가지 조건을 비교할 때.
3. Kruskal-Wallis H 검정 (세 개 이상의 독립된 집단 비교) : 세 개 이상의 독립된 집단에서 중앙값 차이를 비교하는 방법. 정규성이 가정되지 않는 경우 사용.
사용 예시: 세 개 이상의 그룹의 차이를 비교할 때.
4. Friedman 검정 (세 개 이상의 관련된 집단 비교) : 세 개 이상의 관련된 집단 간의 차이를 비교하는 비모수 검정. 주로 반복 측정 데이터를 분석할 때 사용.
사용 예시: 세 가지 이상의 조건에서 측정을 반복한 데이터.
5. Spearman의 순위 상관 계수 (두 변수 간 상관 관계) : 두 변수 간에 비선형적인 관계를 찾을 때 사용하는 비모수 방법. 정규성 가정이 필요하지 않음.
사용 예시: 두 변수 간의 순위 상관 관계를 찾고자 할 때.
6. 부트스트랩 방법 (Bootstrap) : 부트스트랩 방법은 샘플 데이터를 바탕으로 여러 번 재샘플링하여 통계적 추정을 수행하는 방법. 정규성에 대한 가정이 필요 없으며, 작은 표본에서도 사용할 수 있음.
등분산성 조사 : 바틀렛 검정, 레빈 검정. 귀무가설 - 2개 모집단의 분산은 같다. 대립가설 - 2개 모집단의 분산은 같지 않다. p<0.05 귀무가설 기각.
비모수 검정의 대푯값 비교 : 이 때는 평균값 대신 분포의 위치를 나타내는 대푯값에 주목하여 해석.
윌콕슨 순위합 검정 (Wilcoxon rank sum test) : 평균값 대신 각 데이터 값의 순위에 기반하여 검정 실시. 귀무가설 - 2개 모집단의 위치가 같다. 대립가설 - 2개 모집단의 위치가 다르다.
맨-휘트니 U 검정도 동일한 방법.
플리그너-폴리셀로 검정
브루너-문첼 검정
분산분석(ANOVA)
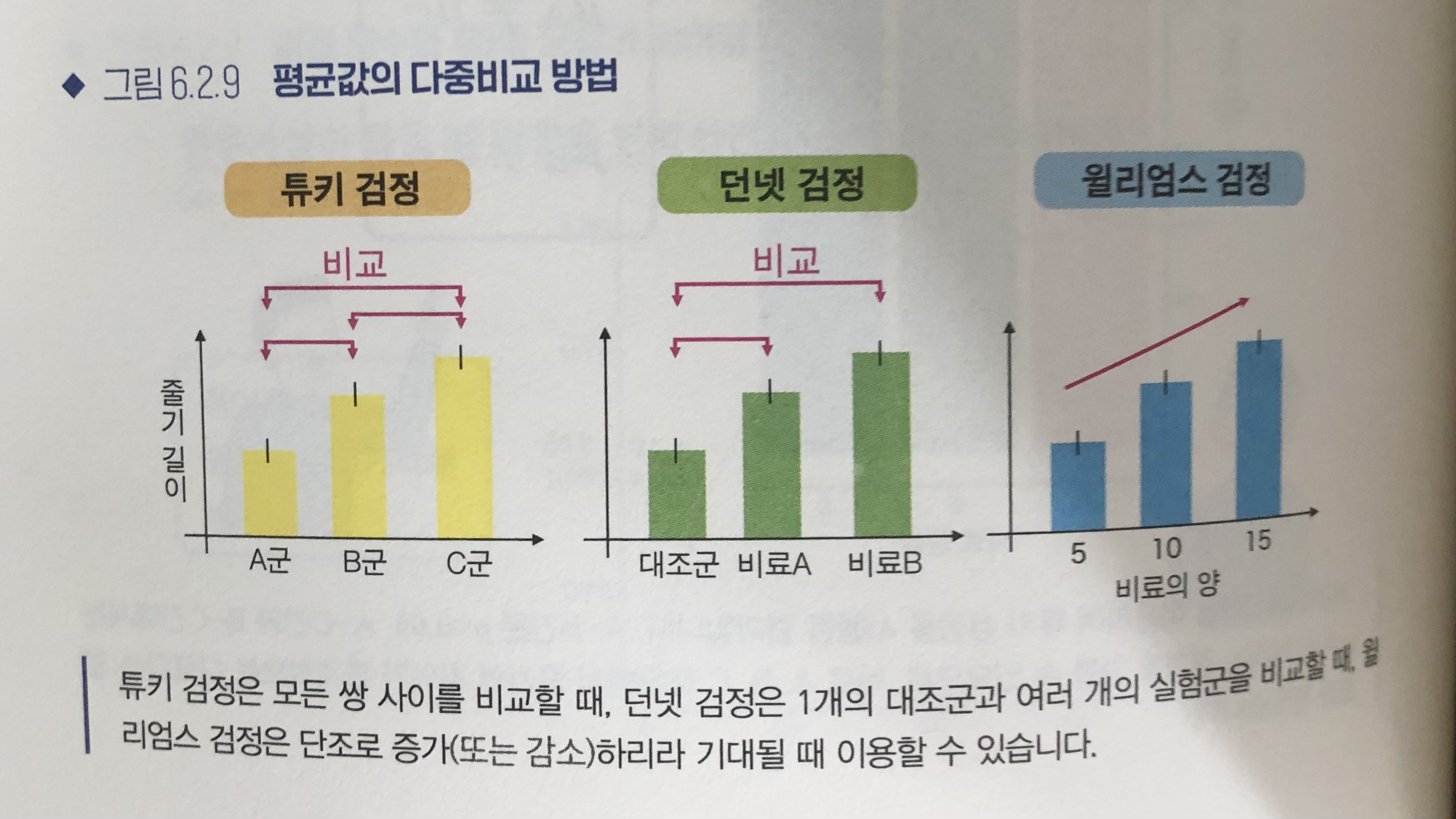
다중비교 검정
본페로니 교정
튜키 검정
던넷 검정
윌리엄스 검정
3집단 이상의 비모수검정
크러스컬-월리스 검정
스틸-드와스 검정 (튜키 검정에 상응)
스틸 검정 (던넷 검정에 상응)
비율 비교 : 이항 검정
귀무가설 - 앞면이 1/2, 뒷면이 1/2의 확률로 나온다. (치우치지 않음)
대립가설 - 앞면이 1/2, 뒷면이 1/2의 확률로 나오지 않는다. (치우침)
카이제곱검정 : 먼저 귀무가설의 확률분포에서 얻을 수 있는 기대도수를 계산. 1) 적합도 검정(귀무 - 모집단은 상정한 이산확률분포이다), 2) 독립성 검정(귀무 - 2개의 변수는 독립이다)
회귀 : y=f(x) 함수로 변수 사이의 관계 공식화.
x : 설명변수, 독립변수
y : 반응변수, 종속변수
피어슨 상관계수 r
스피어만 순위상관계수 p (spearman's rank correlation coefficient p) : 데이터의 x, y 축 중 하나 이상에 정규성이 없을 때. 비모수 상관계수 p 사용.
켄달 순위 상관계수 r도 이와 유사. (표본크기 n이 매우 작을 때; 10 미만)
선형회귀
최소제곱법
회귀계수
신뢰구간, 예측 구간
결정계수 : R^2
R^2이 1에 가까울수록 잘 들어맞음.
선형회귀에서 정규성과 등분산성
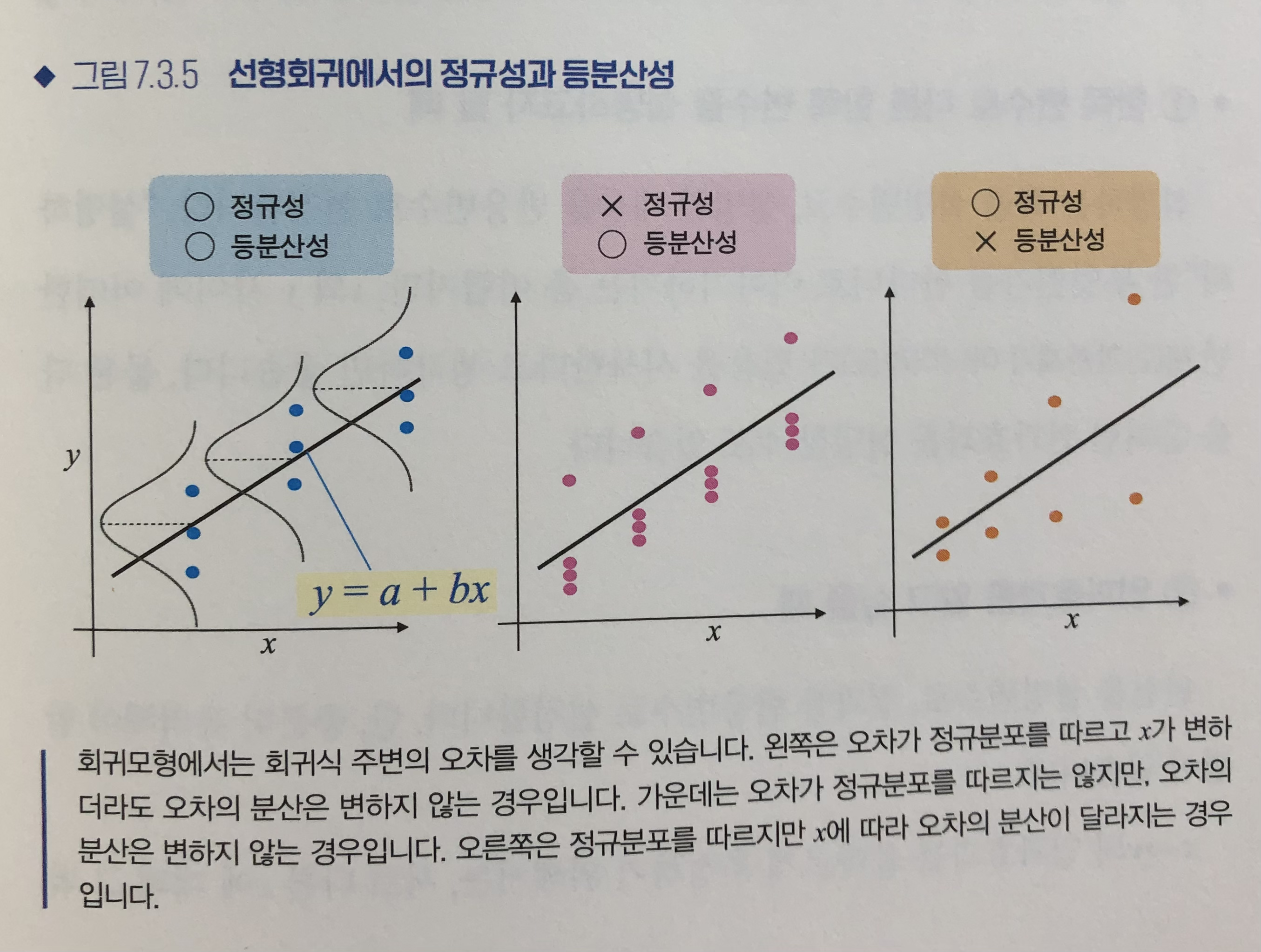
브루쉬-페이건 검정 : 설명변수 x가 변할 때 잔차의 분포가 달라지는지 조사.
다중회귀 : 설명변수가 여러개인 것
회귀평면
편회귀계수 : 상관계수가 1에 가까운 강한 상관이 있을 때는 다중공선성이 있는지 의심하고 대처해야함.
범주형 변수를 설명변수로 : 가변수
공분산분석(ANCOVA) : 일반 분산분석 데이터 + 양적 변수 데이터가 있는 경우. 공변량.
고차원 데이터 : 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가 - 차원의 저주.
다중공선성 : 설명변수가 여러개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우. 추정값의 신뢰성이 떨어짐.
다중공선성 정도를 측정하려면 분산팽창인수 VIF(variance inflation factor)를 계산. VIF 값은 각 설명변수마다 산출됨.
VIF > 10이라면 2개 사이의 상관이 아주 강한 것.
VIF는 상관계수와 밀접하게 관련. VIF=10 이면 상관계수 0.95 정도.
다중공선성이 강한 경우 회귀계수를 해석하기 어려움. 그래서 서로 상관이 있는 변수 중 하나를 없애거나, 주성분분석 등 차원 축소 방법을 이용하여 설명변수의 개수를 줄임. (예측이 목적이 회귀라면 회귀계수가 무엇이든 상관없어 다중공선성도 문제시하지 않는 경우가 흔함)
예측 모델에서 회귀계수가 덜 중요한 이유:
예측의 관점
예측 모델의 목적은 새로운 입력값 X가 주어졌을 때 Y값을 정확히 예측하는 것
이때 중요한 것은 최종 예측값의 정확도이지, 그 과정에서 각 변수가 얼마나 기여했는지가 아님
수학적 설명
Y = β₁X₁ + β₂X₂ + ε 라는 회귀식이 있을 때
X₁과 X₂가 강한 상관관계가 있다면, β₁과 β₂의 값은 불안정하고 신뢰할 수 없음
하지만 β₁X₁ + β₂X₂의 전체 합은 안정적으로 유지됨
즉, 개별 계수는 불안정해도 전체 예측값은 신뢰할 수 있음
해석 vs 예측
회귀계수는 "X가 1단위 증가할 때 Y가 얼마나 변하는가"를 설명함
이는 인과관계나 영향력을 해석하는 데 중요하지만 순수한 예측에서는 이러한 해석이 불필요함
회귀모형의 형태 바꾸기
1. 상호작용 : 설명변수 간의 상승효과
상호작용을 넣으면 해석이 어려워짐
설명변수의 개수가 늘면 상호작용항의 수가 폭발적으로 늘어남
상호작용의 형태는 다양한데도 곱셈으로만 나타냄
설명변수와 상호작용항의 다중공선성 문제가 있음
상호작용항을 적용하는 경우:
상호작용이 있다는 것이 선행연구에서 밝혀지거나 기대되는 때
데이터에 분명한 상호작용이 있을 때
상호작용 유무에 관심이 있을 때
2. 다원배치(이원배치) 분산분석
상호작용항이 유의미하지 않다면 각각의 주효과(main effect)를 그대로 평가.
3. 비선형회귀
예시 : 효소의 화학 반응에서 기질농도와 반응속도의 관계
미하엘리스-멘텐식을 따름. (Lineweaver-Burk plot으로 확인 가능)
파라미터 추정에 컴퓨터를 이용함.
미분계수가 0이 되는 지점이 여러 개일 가능성도 있으므로 국소 최적해에 빠질 위험에도 주의해야함.
근데 왜 비선형인지 궁금해짐. 곡면형 회귀여서 그런지 알아보았음.
비선형적인 관계가 두 개 이상의 변수를 포함하는 경우에 곡면(또는 고차원 곡선)을 형성하는 것과 관련이 있음. 미하엘리스-멘텐 식은 1차원에서 비선형적인 관계를 형성하는 경우에 해당한다고 볼 수 있음.
미하엘리스-멘텐 식은 직접적으로 선형 회귀 분석을 적용하기 어렵지만, 일부 선형화 기법을 사용하여 선형 회귀를 적용할 수도 있음. 예를 들어, Lineweaver-Burk plot은 미하엘리스-멘텐 식을 선형적으로 변환한 그래프임. 하지만 원래 식 자체는 비선형적 .
ML 기반 회귀모델 수업 전 선형대수학 등을 공부하는 것이 좋다.
