🤔 결정트리란?
- 분류와 회귀 문제에 널리 사용하는 모델
- 다중출력도 작업 가능
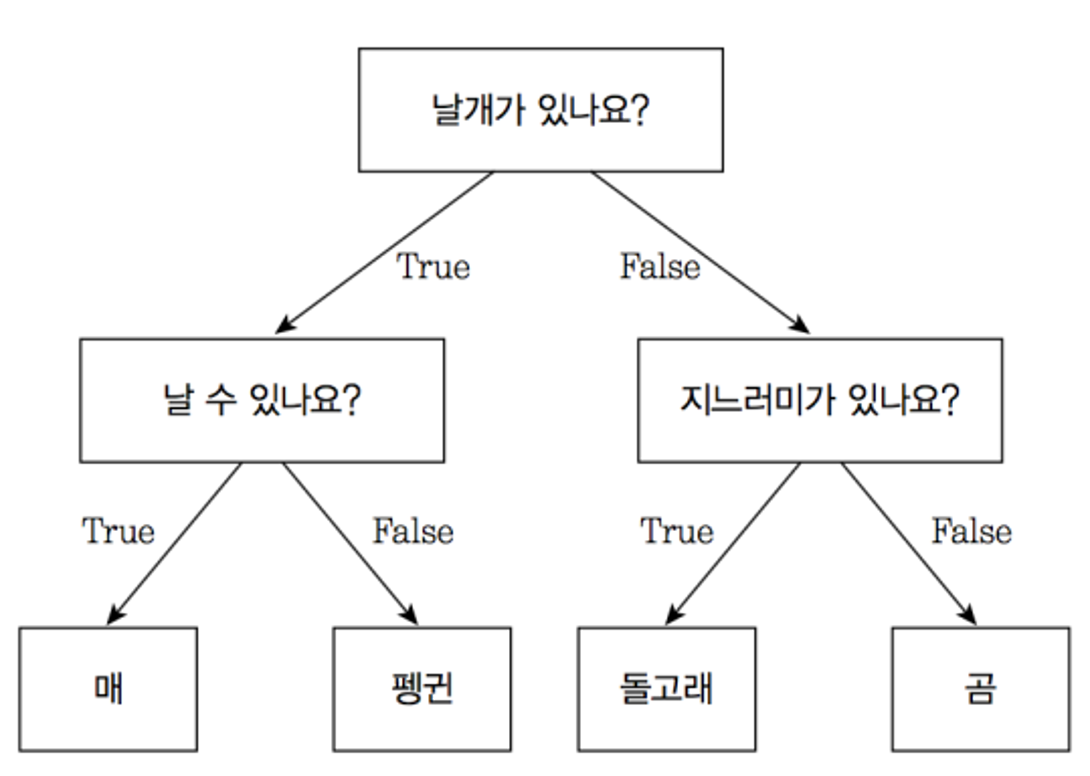
- 결정에 다다르기 위해 예/아니오 질문을 이어 나가면서 학습
Hands On Machine Learning 실습
6.1 결정 트리 학습과 시각화
- 어떻게 예측을 하는지 살펴보는 것을 목적으로 한다.
- 붓꽃 데이터셋에
DecisionTreeCrlassifier을 훈련시키는 코드다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # 꽃잎의 길이와 너비
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth = 2)
tree_clf.fit(X,y)import os
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file = os.path.join("iris_tree.dot"), # image-path -> os.path.join
feature_names = iris.feature_names[2:],
class_names = iris.target_names,
rounded = True,
filled = True
)from graphviz import Source
Source.from_file(os.path.join("iris_tree.dot"))
# sample 속성: 얼마나 많은 훈련 샘플이 적용되었는지 헤아린 것이다.
# 리프 노드의 gini 속성: 불순도를 측정한다. (깊이 1인 왼쪽 노드는 Iris-setosa훈련 샘플만 가지고 있으므로 순수 노드이고 gini점수가 0이다. 깊이 2의 왼쪽 노드는 1-(0/54)**2 - (49/50**2 - (..)))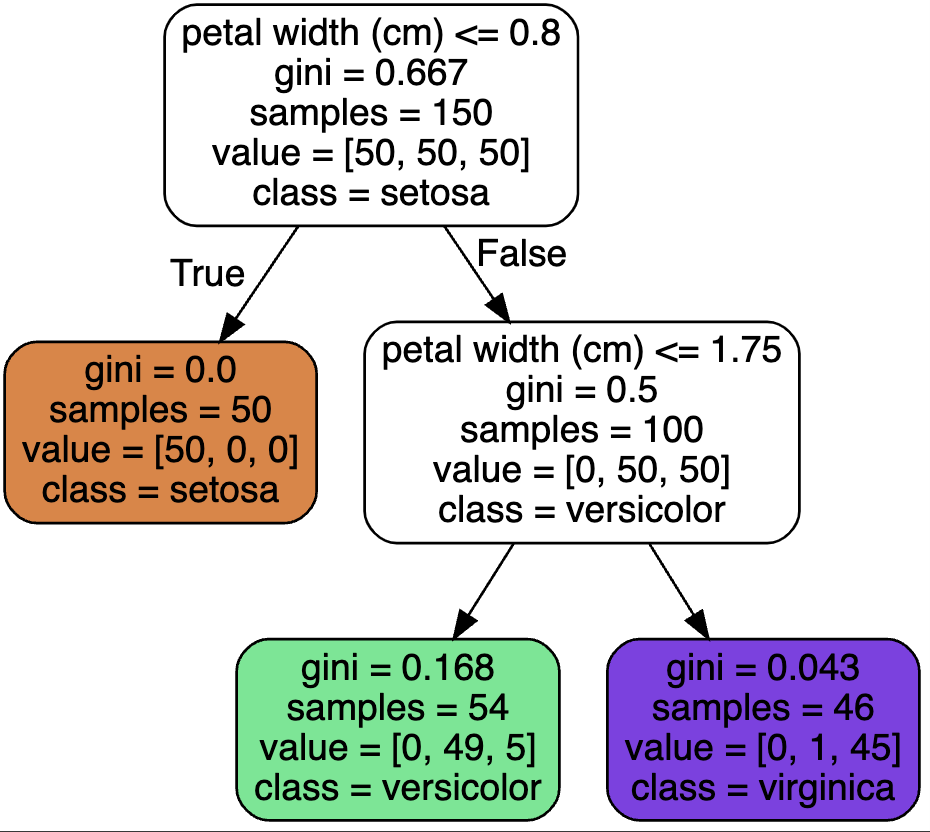
6.2 예측하기
- 트리가 어떻게 예측을 만들어내는가?
- 루트 노드 : 깊이가 0인 맨 꼭대기의 노드
- 리프 노드 : 자식 노드를 가지지 않는 노드
- 불순도를 측정하는 방법 ➡️ 지니 불순도
- 깊이가 1이면 2개로 나뉘어지고, 깊이가 2이면 2분할, 3으로 하면 깊이 2의 두 노드가 각각 결정 경계를 추가로 만들게 된다.
6.3 클래스 확률 추정
- 한 샘플이 특정 클래스 k에 속할 확률을 추정할 수 있다.
tree_clf.predict_proba([[5,1.5]]) # [길이, 너비]
>>> array([[0. , 0.90740741, 0.09259259]])tree_clf.predict([[5,1.5]])
>>> array([1])6.4 CART 훈련 알고리즘
- 사이킷런은 결정 트리를 훈련시키기 위해 CART 알고리즘을 사용한다.
- classification and regression tree Algorithm
- k:하나의 특성, t_k: 특성 k의 임계값
- CART 알고리즘이 훈련세트를 성공적으로 둘로 나누었다면 같은 방식으로 서브셋을 또 나누고 또 나누고... 반복
- 그래서 언제 끝나느냐?: 최대 깊이가 되거나 불순도를 줄이는 분할을 찾을 수 없을 때
6.5 계산 복잡도
- 루트 노드 ➡️ 리프 노드
- 약 O(log_2(m))
- 각 노드는 하나의 특성값만 확인하기 때문에 특성의 수와 무관하게 O(log_2(m))이다.
6.8 회귀
import numpy as np
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth = 2, random_state = 42)
tree_reg.fit(X, y)export_graphviz(
tree_reg,
out_file = os.path.join("regression_tree.dot"),
feature_names = ["x1"],
rounded = True,
filled = True
)
Source.from_file(os.path.join("regression_tree.dot"))텐서플로우 참고하여 추가 학습
결정트리 만들기
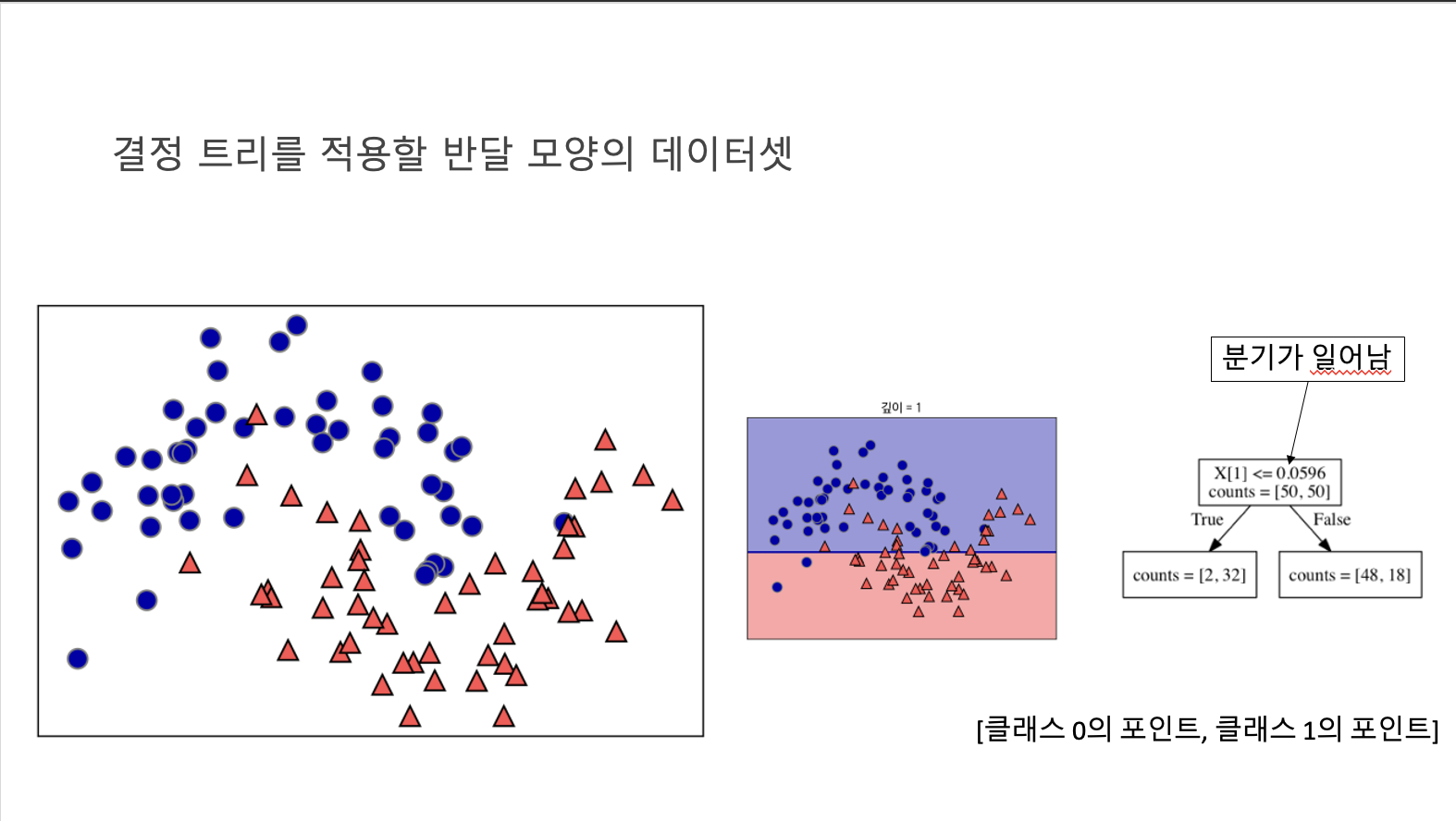
- 직선이 의미하는 x[1]<=0.0596의 테스트에서 분기가 일어난다.
- 이 테스트를 통과하면 포인트는 왼쪽 노드에 할당되는데 이 노드에는 클래스 0에 속한 포인트는 2개, 클래스 1에 속한 포인트는 32개다.
- 그렇지 않으면 포인트는 오른쪽 노드에 할당되며 이 노드에는 클래스 0의 포인트 48개, 클래스 1의 포인트 18개가 포함되었다.
- 이 두 노드는 그림의 윗부분과 아랫부분에 해당합니다. 첫 번째 분류가 두 클래스를 완벽하게 분류하지 못해서 아래 영역에는 아직 클래스 0에 속한 포인트가 들어 있고 위 영역에는 클래스 1에 속한 포인트가 포함되어 있다.
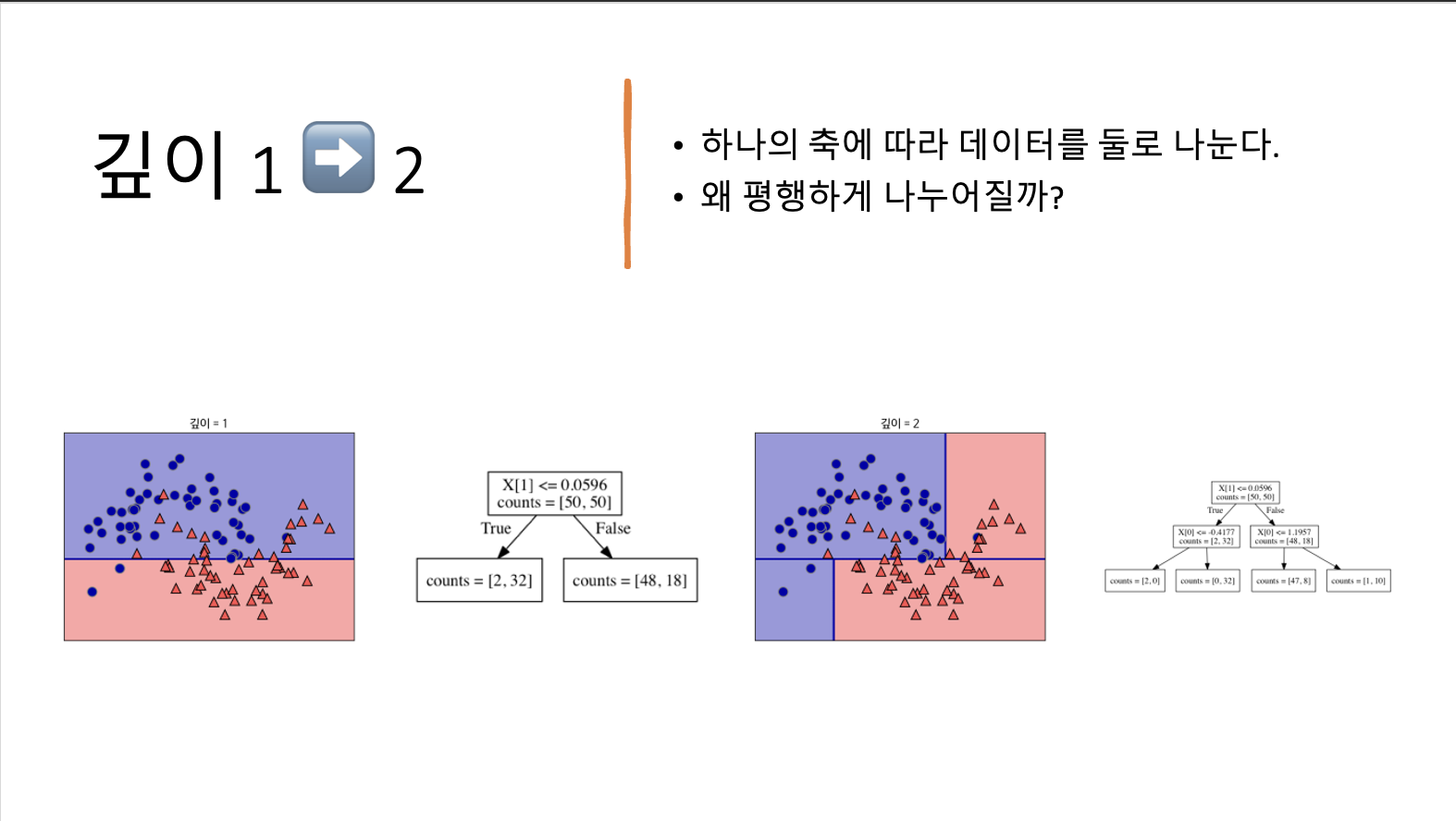
- 각 테스트는 하나의 축을 따라 데이터를 둘로 나누는 것으로 생각할 수 있다.
- 각 테스트는 하나의 특성에 대해서만 이루어지므로 나누어진 영역은 항상 축에 평행하다.
- 데이터를 분할하는 것은 각 분할된 영역이 (결정 트리의 리프) 한 개의 타깃값(하나의 클래스나 하나의 회귀 분석 결과)을 가질 때까지 반복된다.

타깃 하나로만 이뤄진 리프 노드를 순수 노드pure node라고 한다.
Q. 여기서 예측을 어떻게 하는가?
새로운 데이터 포인트에 대한 예측은 주어진 데이터 포인트가 특성을 분할한 영역들 중 어디에 놓이는지를 확인하면 된다.
그래서 그 영역의 타깃값 중 다수(순수 노드라면 하나)인 것을 예측 결과로 한다. 루트 노드에서 시작해 테스트의 결과에 따라 왼쪽 또는 오른쪽으로 트리를 탐색해나가는 식으로 영역을 찾을 수 있다.
같은 방법으로 회귀 문제에도 트리를 사용할 수 있다. 예측을 하려면 각 노드의 테스트 결과에 따라 트리를 탐색해나가고 새로운 데이터 포인트에 해당되는 리프 노드를 찾는다. 찾은 리프 노드의 훈련 데이터 평균 값이 이 데이터 포인트의 출력이 된다.
일반적으로 트리 만들기를 모든 리프 노드가 순수 노드가 될 때까지 진행하면 모델이 매우 복잡해지고 훈련 데이터에 과대적합된다. ➡️ 즉, 정확도가 100이 된다.➡️ 즉 훈련 세트의 모든 데이터 포인트는 정확한 클래스의 리프 노드에 있습니다.
위의 그림에서 오른쪽 그래프를 보면 과대적합된 것으로 볼 수 있다.
결정 경계가 클래스의 포인트들에서 멀리 떨어진 이상치 outlier 하나에 너무 민감하다.
복잡도를 제어
사전 가지치기- 트리의 최대 깊이나 리프의 최대 개수를 제한
- 노드가 분할하기 위한 포인트의 최소 개수를 지정하는 것
사후 가지치기
scikit-learn에서 결정 트리는 DecisionTreeRegressor와 DecisionTreeClassifier에 구현되어 있습니다. scikit-learn은 사전 가지치기만 지원한다.
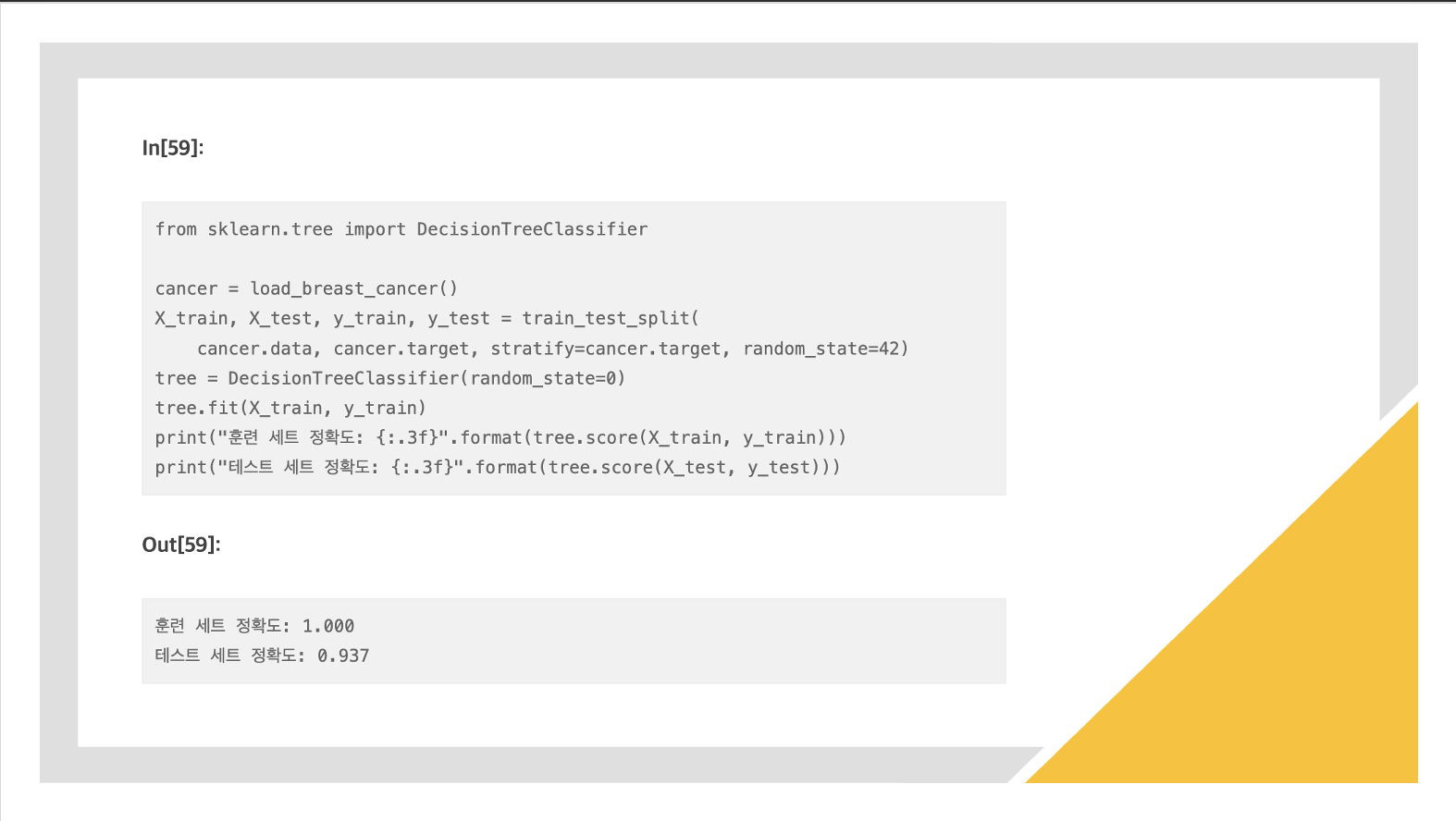
과적합 모델
-
모든 리프 노드가 순수 노드이므로 훈련 세트의 정확도는 100%입니다.
-
테스트 세트의 정확도는 이전에 본 선형 모델에서의 정확도인 95%보다 조금 낮다.
-
훈련 세트의 정확도는 당연히 1이 되고, 테스트 세트의 정확도는 93퍼센트가 된다.
사전 가지치기를 트리에 적용한 모델

"일정 깊이에 도달하면 트리의 성장을 멈추게 하는 것"
- max_depth=4 옵션을 주면 연속된 질문을 최대 4개로 제한한다.
- 트리 깊이를 제한하면 과대적합이 줄어든다.
- 이는 훈련 세트의 정확도를 떨어뜨리지만 테스트 세트의 성능은 개선시킨다.
분류 알고리즘은 어떻게 쓰이는가?
- 분류 알고리즘
Logistic RegressionSVMDecision Tree
이때까지 배웠던 SVM, Logistic Regression, Decision Tree은 분류문제에 쓰이는 알고리즘이었다.
이것들이 그런데 각각 다른 용도로 하나씩 쓰이는지 의문점을 갖게 되었다.
앙상블: 여러개를 혼합하여 사용한다.
각각의 알고리즘은 따로 쓰일 수도 있겠지만, 역시 각자 장단점이 존재하기 때문에 서로 보완해주기 위해서 같이 혼합하여 쓰이는 경우가 많았다.
Bagging(자루넣기): 똑같은 일을 여러개 시키고 나서, 잘되는 점수만 뽑아간다.
Stacking(쌓기): 하나를 실행시켜서 나온 결과를 모아서 다른 곳에 또 넣어서 결과를 본다.
Boosting(밀어주기): 다른데서 정보를 살짝 받아서 진행한다.
앙상블 예제
앙상블된 실제 사례가 궁금해서 찾아보았다.
SVM과 Decision Tree를 이용한 혼합형 침입탐지 모델에 관한 논문을 찾게 되었다.




SVM은 이산형 데이터를 이용하지 못하기에 Decision Tree로 이를 보완하였다고 한다. 이를 통해 확연히 탐지율이 향상되었음을 확인할 수 있었다고 한다.
스터디에서 그런데 저 마지막 자료 화면에 "향후로는 ~~~ 연구가 필요하다." 파트에서 한 스터디원이 내가 미처 생각하지 못했던 점을 지적해주셨다.
이 논문이 나온 시기는 2007년으로 상당히 오래된 시점이었다. 그리고 뒤에 이어지는 논문을 보니 최근의 논문도 존재했으며 이것 역시 SVM와 Decision Tree를 앙상블하여 사용하였다.
즉, "이미 나름 충분한 연구가 이루어져서 탐지 시간을 줄이기 위해 학습 데이터 양을 조절하는 방법을 고안하지 않았을까?"
라는 의문점이다.
이에 관해서는 다음 Chapter7에서 앙상블 방법을 다루고 있는데 그때 더 자세하게 정리하도록 하겠다!

