

Life is a maze and love is a riddle (인생은 미로 사랑은 수수께끼)
생각해봅시다!!
- 검은 방을 흰 방으로 바꾸어야 할 최소의 수... 라고 생각하시니까 문제가 복잡해지는 겁니다.
- 이렇게 시각을 전환하면 어떨까요?
- 검은 방도 지나갈 수 있지만, 지나갈 때
1의 거리 비용이 발생한다. - 흰 방은 지나가도 비용이 발생하지 않는다.
- 검은 방도 지나갈 수 있지만, 지나갈 때
- 그러면 이 문제를 시작점에서 끝점까지 이동하는 최단 거리을 구하는 문제로 바꿔 풀 수 있습니다.
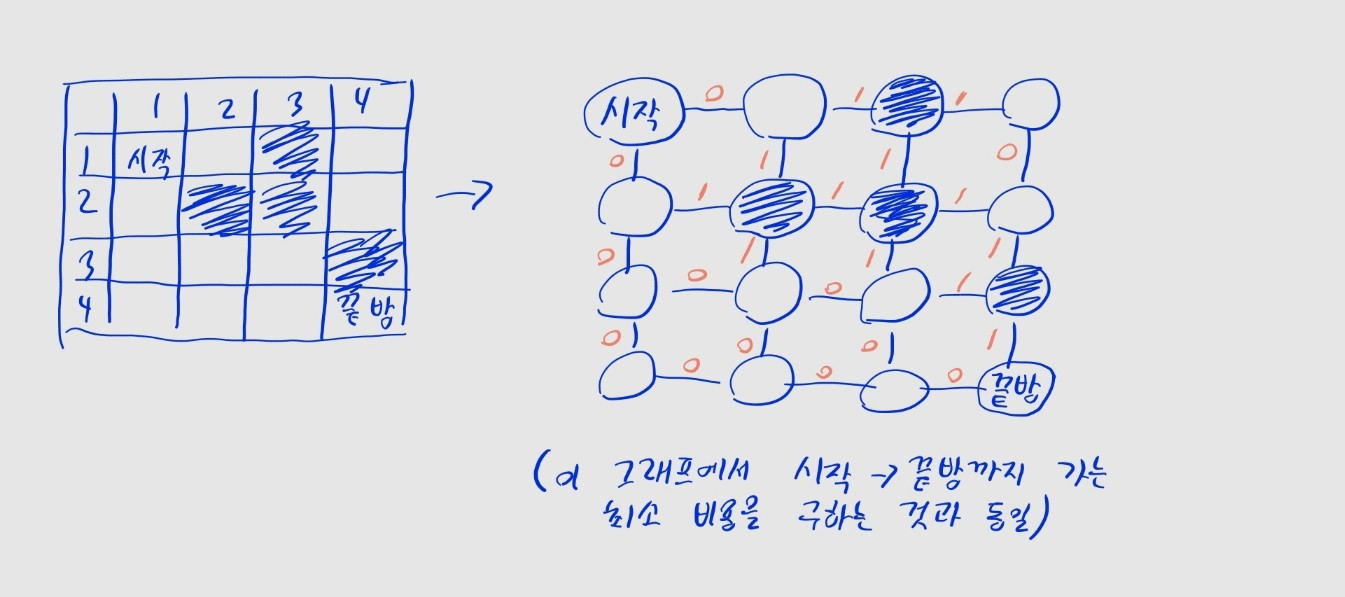
다익스트라 알고리즘
- 방을 노드, 방과 방 사이를 간선이라고 했을 때, 비용이
1인 간선도 있고0인 간선도 있습니다. - 비용이 간선마다 다르니까, 다익스트라 알고리즘을 쓰면 되겠군요.
- 알고리즘이 종료된 후, 첫 방에서 마지막 방까지의 비용을 정답으로 출력하면 됩니다.
2차원 최단거리 테이블 만들기
# 미로의 시작 칸과, 미로 각 칸의 거리
N = int(input())
grid = [] # 미로 정보
for _ in range(N):
grid.append(list(map(int, input().strip())))
INF = float('inf')
# 미로의 시작 칸과, 미로 각 칸의 거리
distance = [[INF] * N for _ in range(N)]- 일반적인 다익스트라와 다르게 2차원 배열로 구성된 미로를 탐색해야 합니다.
- 즉 최단거리를 저장할 테이블도 2차원이여야겠죠?
distance[i][j]는 미로의 시작 칸과, 미로의i행j열 칸 간 최단 거리를 나타냅니다.
시작점 설정
def djikstra():
# (거리, x좌표, y좌표) 꼴로 푸시
queue = []
# 시작점 x=0 y=0, 거리는 0으로 설정
heapq.heappush(queue, (0, 0, 0))
distance[0][0] = 0
# 상, 좌, 하, 우 순서대로
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]
# (이후코드에서 계속)- 마찬가지로 우선순위 큐에도 튜플
(거리, x좌표, y좌표)를 푸시해줍니다. heappop으로 원소를 꺼낼 때는, 첫 값인거리가 최솟값인 튜플부터 반환됩니다.
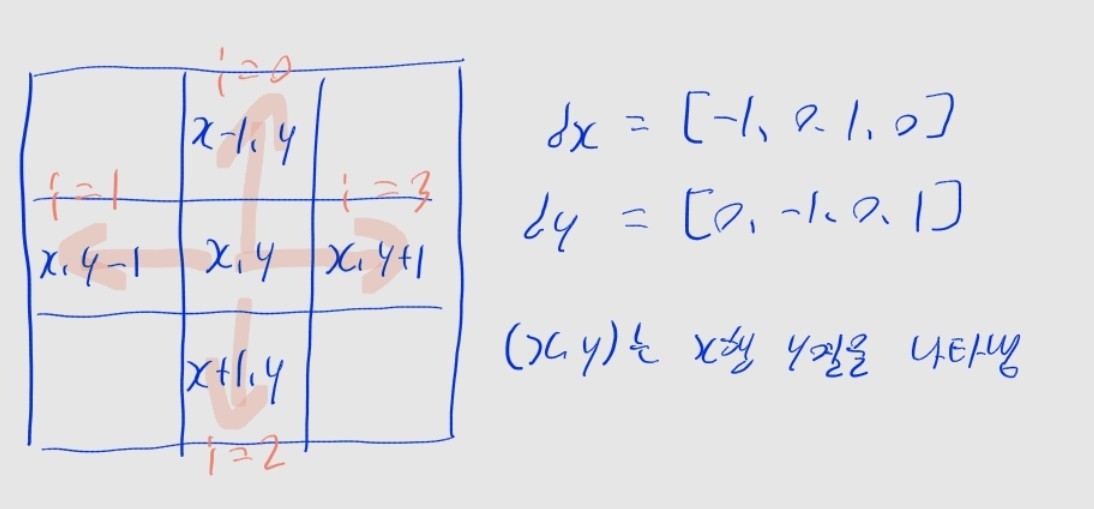
다익스트라 알고리즘
def djikstra():
# (이전코드에서 계속)
# 다익스트라 알고리즘
while queue:
dist, x, y = heapq.heappop(queue)
if distance[x][y] < dist:
continue
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
# 범위를 안 벗어나는지 확인
if 0 <= nx < N and 0 <= ny < N:
if grid[nx][ny] == 1: # 흰 방 (1)
new_dist = dist
else: # 검은 방 (0)
new_dist = dist + 1
# 기존에 구한 거리보다 짧으면 갱신 및 힙에 푸시
if new_dist < distance[nx][ny]:
distance[nx][ny] = new_dist
heapq.heappush(queue, (new_dist, nx, ny))- 현재
(x, y)와 인접한(nx, ny)를 확인하는 부분에선i를 순회하며dx[i],dy[i]을x,y에 더해nx,ny를 계산함으로써, 상하좌우를 둘러보는 식으로 구현할 수 있습니다.
- 인접한 좌표가
- 흰 방이면 비용이 소요되지 않으므로, 비용 계산은 큐에서 꺼내온
dist를 그대로 사용합니다. - 검은 방이면 1의 비용이 들기 때문에, 비용 계산은
dist에 1을 더해 주어야 합니다.
- 흰 방이면 비용이 소요되지 않으므로, 비용 계산은 큐에서 꺼내온
- 나머지는 일반적인 다익스트라 알고리즘과 비슷합니다.
- 이후 다익스트라 함수를 실행한 뒤,
print(distance[-1][-1])로 마지막 칸까지의 최단거리를 출력하면 됩니다.
풀이
import heapq
import sys
input = sys.stdin.readline
N = int(input())
grid = [] # 미로 정보
for _ in range(N):
grid.append(list(map(int, input().strip())))
INF = float('inf')
# 미로의 시작 칸과, 미로 각 칸의 거리
distance = [[INF] * N for _ in range(N)]
def djikstra():
# (거리, x좌표, y좌표) 꼴로 푸시
queue = []
# 시작점 x=0 y=0, 거리는 0으로 설정
heapq.heappush(queue, (0, 0, 0))
distance[0][0] = 0
# 상, 좌, 하, 우 순서대로
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]
# 다익스트라 알고리즘
while queue:
dist, x, y = heapq.heappop(queue)
if distance[x][y] < dist:
continue
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
# 범위를 안 벗어나는지 확인
if 0 <= nx < N and 0 <= ny < N:
if grid[nx][ny] == 1: # 흰 방 (1)
new_dist = dist
else: # 검은 방 (0)
new_dist = dist + 1
# 기존에 구한 거리보다 짧으면 갱신 및 힙에 푸시
if new_dist < distance[nx][ny]:
distance[nx][ny] = new_dist
heapq.heappush(queue, (new_dist, nx, ny))
djikstra()
# 첫 칸에서 마지막 칸까지 거리
print(distance[-1][-1])시간 복잡도
- 미로의 행 및 열 수를 으로 둘 때
- 미로 입력을 받는 데 .
- 다익스트라 알고리즘의 시간복잡도는, 노드 수를 , 간선 수를 로 뒀을 때
- 노드 수 -> 개(모든 방),
- 간선 수 -> 각 방은 상하좌우로 최대 4개 방과 연결되므로, 최대 개
- 즉 시간복잡도는
- 최종 , 이므로 시간초과가 날 일은 없음.
기억할 점
- 통과하게 되는 장애물의 수를 구하는 문제는, 0과 1의 가중치만을 가진 간선으로 이루어진 그래프에서 다익스트라 알고리즘을 수행하는 문제로 바꿔 풀 수 있다.
