[알고리즘] 부분합, 누적합

부분합, 누적합

• 배열의 일부 구간에 대한 합을 빠르게 구할 수 있게 해주는 스킬
• n개의 원소로 이루어진 배열이 주어졌을 때 반복문을 통해 배열의 합을 구하려면 $O(n)$이 걸리는데 부분합을 이용하면 모든 부분합을 $O(1)$에 바로 구하기 가능

1차원 배열

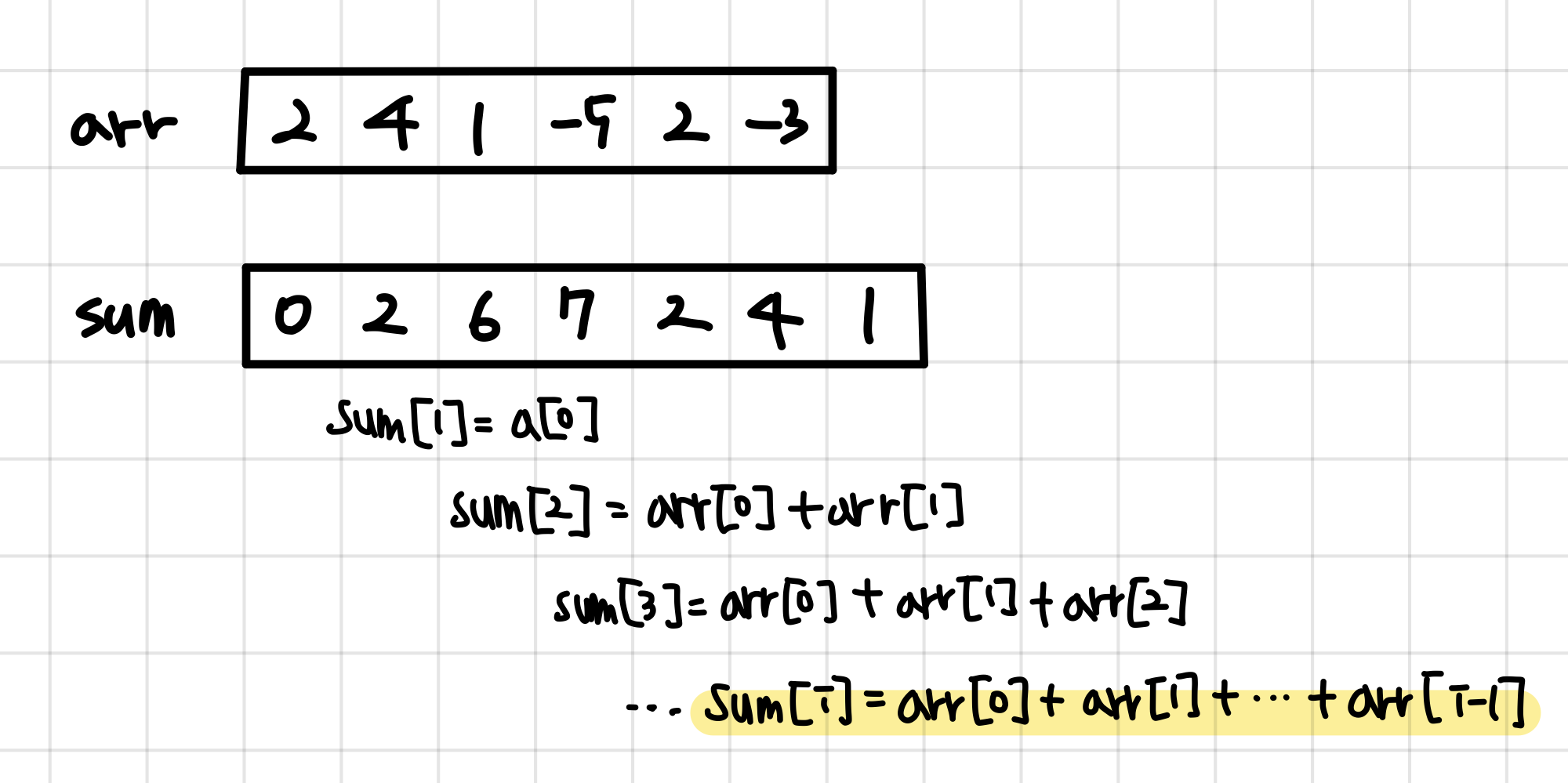
활용법

2차원 배열

점화식: sum[i][j] = arr[i-1][j-1] + sum[i-1][j] + sum[i][j-1] -sum[i-1][j-1]

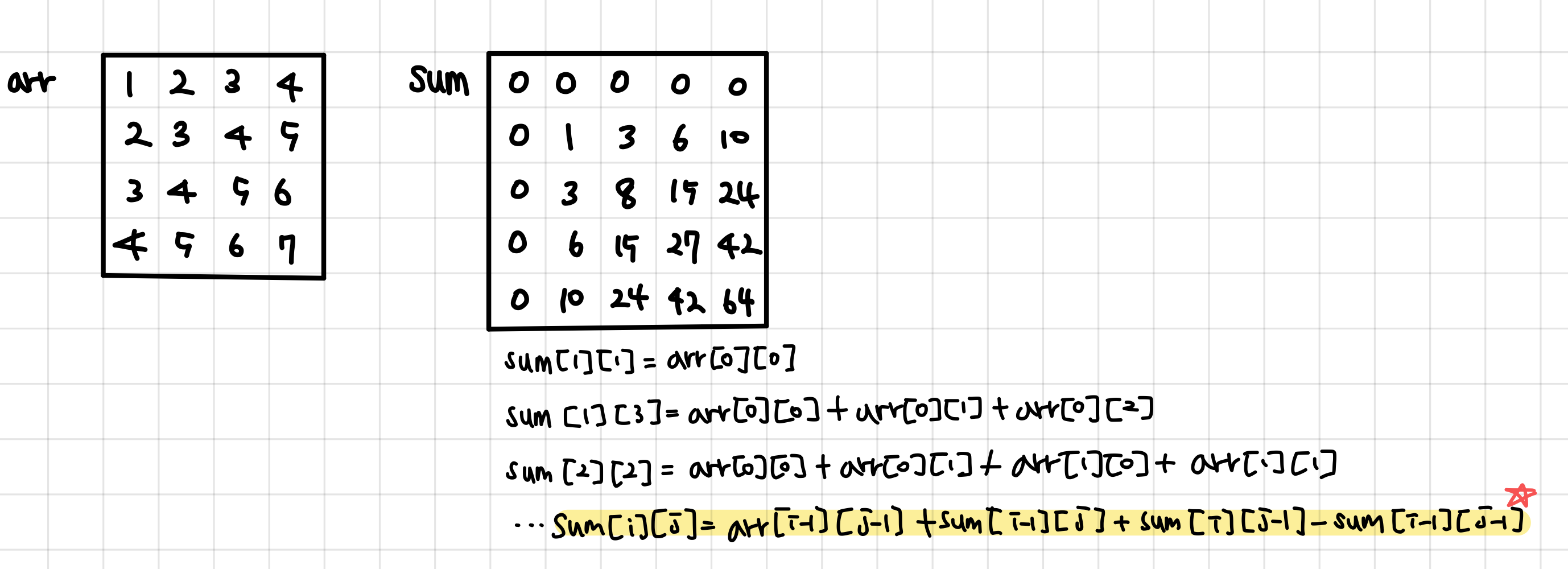
⭐️ 활용법

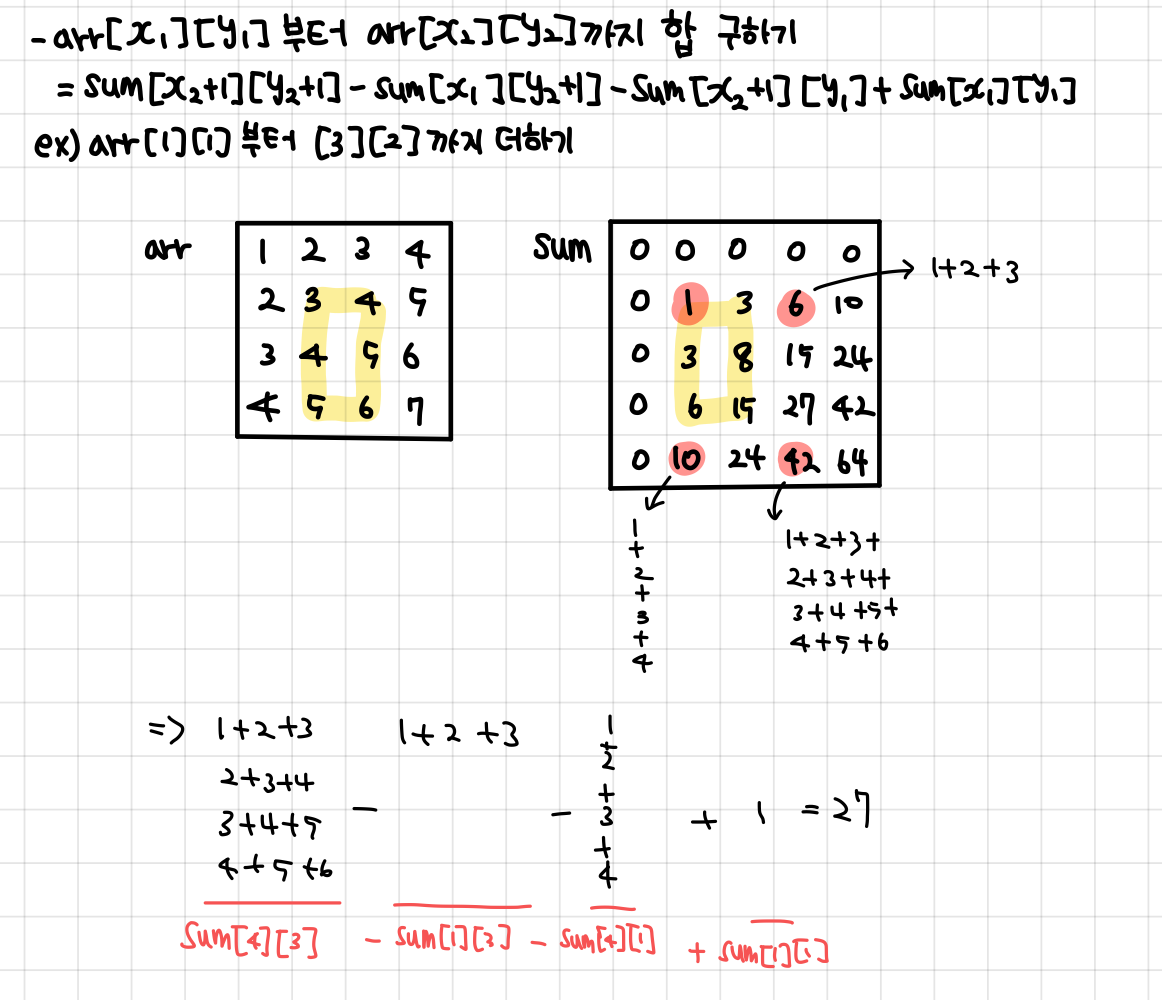
• arr의 (x1,y1)부터 (x2,y2)까지 합
  = sum[x2+1][y2+1] - sum[x1][y2+1] - sum[x2+1][y1] + sum[x1][y1]
  

https://yiyj1030.tistory.com/489