[논문 : NLP] Class-Based n-gram Models of Natural Language

임수정·2022년 3월 10일

NLP

목록 보기

3/4

[논문 정보]

Author : Peter F.Brown 외 4명
Paper Link : https://aclanthology.org/J92-4003/
Year : 1992
Venue: Computational Linguistics, Volume 18

[Abstract]

저자가 풀려고 하는 문제(노란색)
- 텍스트에서 이전 단어들이 주어지면 다음 단어를 예측하는 task(= Language Model 구축)
제안 방안(초록색1)
- 단어를 클래스로 분류하고, 그 클래스를 이용해 n-gram 모델을 만들자.
제안 방안에 대한 직관(초록색2)
- 단어 간 동시 발생 빈도(co-occurrence)를 고려해 단어에 클래스를 부여
- 자주 같이 출현하면 비슷한 클래스일 수 있다.
제안 방안에 대한 증명(파랑색)
- syntactically(문법적으로), semantically(의미적으로) 그룹지었을 때 두 경우에서 모두 단어들의 클래스를 뽑아낼 수 있음을 보임

[Introduction]

구체적인 문제 상황 & 목표
- Task
  - 텍스트에서 이전 단어들이 주어지면 다음 단어를 예측하는 task(= Language Model 구축)
- Problem
  - 일부 단어가 노이즈가 있는 채널을 통과하면 왜곡되는데, 왜곡된 단어를 복원하지 못하는 문제가 존재
  - 이 문제를 해결하기 위해서는 어떤 단어가 노이즈가 있는 채널에 들어갈 지에 대한 확률을 예측해야 함
- Goal
  - 어떤 단어가 왜곡될지(노이즈가 있는 채널에 들어갈 지)에 대한 확률 예측
  - 추가적으로, 통계적 방법으로 단어들을 군집화(클래스로 분류)하는 과정도 진행
논문 진행 과정
- Language Model 소개, n-gram 소개
- 단어들을 그룹화, 즉 클래스로 분류하여 n-gram model을 만드는 방법 소개
- 서로 다른 두 개의 단어 그룹에 mutual information을 적용해 본 실험 설명
참고 사항 (논문에 실제로 쓰여 있던 부분이다. 신기..)
- 이 논문은 수학적, 특히 통계적 표기나 정의를 자유롭게(?~~무자비하게~~) 사용한다.
- 따라서 통계적 표기나 정의 등이 익숙하지 않은 독자의 경우 아래 두 논문을 읽고 오는 것을 추천
  - Feller, W. (1950).
    An Introduction to Probability Theory and its Applications, Volume I. John Wiley & Sons, Inc.
  - Gallagher, R. G. (1968).
    Information Theory and Reliable Communication. John Wiley & Sons, Inc.
- 독자들이 논문을 읽으며 집중해야 할 부분(= 미리 알고 오면 좋을 부분)
  - Conditional probabilities
  - Markov chains
  - Entropy
  - Mutual Information

<잠깐 개념 정리>

위에서 4가지 개념을 미리 알아오라고 했으니.. 간단히 살펴보자 (~~논문에서 설명해주면 좋으련만..~~)

1. Conditional probabilities (조건부 확률)

주어진 사건이 일어났다는 가정 하에 다른 한 사건이 일어날 확률
A라는 사건이 일어났을 때, B라는 사건이 일어날 확률은 다음과 같이 식으로 표현된다.
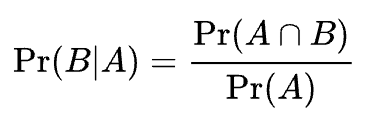
위의 식을 좀 건드려보면, 사건 A,B의 교집합의 확률은 다음과 같이 나타낼 수 있다.
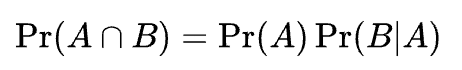
즉, 두 사건이 동시에 일어날 확률은 사건 A가 일어날 확률과 A가 일어났을 때 B가 일어날 확률의 곱이다.
보다 일반적으로, 임의의 n개의 사건 $A_1, ..., A_n$ 에 대하여 $\displaystyle \operatorname {Pr} (A_{1}\cap \cdots \cap A_{n-1})>0$ 이라면,
아래 식이 성립한다.
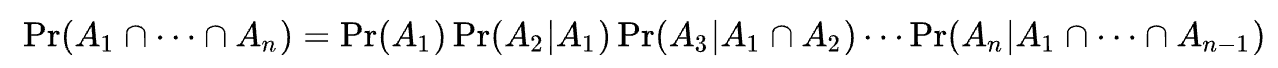
추가적으로 두 사건 중 하나라도 양의 확률을 가질 경우 다음 조건이 서로 동치 이다.
$Pr(B|A) = Pr(B)$ $\Leftrightarrow$ 두 사건 A, B는 독립이다.
즉, 두 사건 A, B가 독립이라면 A가 일어나든 일어나지 않든 B는 영향을 받지 않을 것이므로 A 사건의 전제의 유무의 관계없이 확률이 동일한 것이다.
또한 A, B가 독립일 때 사건 A,B의 교집합은 $Pr(A \cap B) = Pr(A)Pr(B|A) = Pr(A)Pr(B)$ 로 표현된다.

2. Markov chains (마르코프 연쇄) : '마르코프 특성'을 지니는 '이산 확률과정'

정의도 어려운데, 하나씩 살펴보자.
먼저 '확률 과정' = '어떤 사건이 발생할 확률이 변화하는 과정'을 의미한다.
'이산'시간 = '시간이 연속적으로 변하지 않고 이산적으로 변하는 것'을 의미한다.
'마르코프 특성'= '과거 상태들과 현재 상태가 주어졌을 때, 미래 상태는 과거 상태와는 독립적으로 현재 상태에 의해서만 결정된다는 것'이다.
다시 말해, 과거와 현재 상태 모두를 고려했을 때 미래 상태가 발생할 확률과 현재 상태만을 고려했을 때 미래 상태가 발생할 확률이 동일하다는 것이다.
기억나는 마르코프 프로세스의 예시를 들면, 우리가 자동차를 운전할 때 다음에 브레이크를 밟을지 엑셀을 밞을지 방향을 틀지 등을 선택하기 위해 필요한 정보는, 지금 당장 보이는 길의 모양과 지금 내가 브레이크를 밟고 있는지, 엑셀을 밟고 있는지에 대한 정보이다. 사실 그 이전에 이 사람이 운전을 어떻게 해왔고, 이전 길이 어떻게 생겼었는지는 다음 행동 예측과는 무관한 정보이다.)
이를 식으로 나타내면 다음과 같다.
$Pr(X_{n+1}|X_n) = Pr(X_{n+1}|X_1, X_2, ..., X_{n-1}, X_n)$
마코프 프로세스는 이처럼 과거 상태를 기억하지 않기 때문에 메모리리스(memoryless) 프로세스로 불린다. 또한 마코프 프로세스는 마코프 체인(Markov chain, MC)이라 불리기도 한다.
조금 더 자세한 설명을 링크를 첨부한다 : https://bskyvision.com/573

3. Entropy

Entropy : 정보를 표현할 때 필요한 최소 자원량
- What is a common currency of information?(정보를 어떻게 일반화해서 보여줄 수 있을까?)
  - 언어도 정보의 하나인데, 일본어, 한국어, 영어 모두 표현방식이 다르다.
  - 이러한 정보들을 표현하는 통용된 방식을 만들 수는 없을까?
정리하는데 참고했던, Entropy와 Mutual Information을 너무 잘 설명해놓은 영상이 있어서 첨부한다.
: https://www.youtube.com/watch?v=z1k8HVU4Mxc

4. KL Divergence, Mutual Information

어떤 식으로 해결하고자 했는가. 어떤 장점이 있는가(시간 여유가 된다면, 이전에는 어떤 방법이 있었고 그 방법들의 단점)
- 1. Language Model
- 1. 단어가 클래스로 분류되는 n-gram model - 바로 옆 클래스끼리의 mutual information이 크다.
- 1. mutual information을 다른 word clustering 방식에 적용
그 방법에 대한 intuition (수학 없이)
방법에 대한 이해(수학적으로)
방법의 성공성을 보여주기 위해 사용한 데이터, 메트릭, 성능비교
부족하다 생각되는 것, 애매한 것, 혹은 좋았던 점 등의 Discussion point

Mutual Information
Perplexity

Q. 질문:
mutual information과 loss in average mutual information과 다른점 ?
loss in average MI가 적은애들을 merge한다라는게 비슷한 의미를 가진 단어끼리 merge한다라고 해석하는게 맞나?
MI가 두 단어의 상관성을 나타내고, 비슷한 의미의 단어끼리 같은 클래스로 merge해야하기 때문에 MI가 큰 애들끼리는 묶어야한다고 이해할 수 있는데 loss in average MI가 적은애들끼리 merge한다고 해서 잘 이해가 안됨.

논문의 473page 두번째 문단에 정의는 돼있는데 \Ik, \I_k(i,j)의 정의에 대한 전개가 위에 쭉 있는데 그걸 놓쳐서 정확하게 이해를 못하겠음. \I{k-1} = \I_k(i,j) 로 연결지어 생각했을 때 k 번째 sequence의 페어 i,j의 MI에서 (k-1)번째 sequence의 페어 i,j페어 의 MI를 뺀 값?으로 생각할 수 있는 것 같은데..

답변:

우리가 낮춰야 하는 loss값
$L_k(i,j) = I_k - I_k(i, j)$

논문에서

the average mutual information( $I_k$ ) remaining after we merge $C_k(i)$ and $C_k(j)$

라고 했으므로 실질적으로 loss( $L_k(i,j)$ )를 낮추려면 $- I_k(i, j)$ 을 낮춰야 함. 즉 $I_k(i, j)$ 값을 키워야 함.
그러니 $i, j$ 는서로 의존도가 높은 애들끼리 merge를 한다고 이해하는 게 맞을 것 같습니다.

조금 더 자세히 보면, 논문 수식에서 아래와 같은 수식이 나옵니다.

$I_k(i,j)$

$= I_k - s_k(i) - s_k(j) + q_k(i,j) + q_k(j, i) + q_k(i +j, i +j) + \sum_{l}{q_k(l,i + j)} + \sum_{m}{q_k(i + j,m)}$

--> 식을 좌변 우변으로 넘기고 넘기면,

$s_k(i) + s_k(j) - q_k(i,j) - q_k(j, i) - q_k(i +j, i +j) - \sum_{l}{q_k(l,i + j)} - \sum_{m}{q_k(i + j,m)} = I_k - I_k(i,j) = L_k(i,j)$

이렇게 $L_k(i,j)$ 를 풀어 쓴 식을 해석해보면
$i/j$ 와 다른 것들의 평균 의존성( $s_k(i)$ , $s_k(j)$ )은 낮추고,
$i, j$ 끼리의 의존성( $q_k(i,j)$ , $q_k(j, i)$ )은 높이고,
i+j(merge 한 것)과 다른 것들 간의 평균 의존성
( $\sum_{l}{q_k(l,i + j)}, \sum_{m}{q_k(i + j,m)}$ )은 높이게(개연성을 위해) 학습이 되는 것 같습니다.