xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems 논문 및 정리

우수민·2021년 4월 12일

논문 기록

목록 보기

9/10

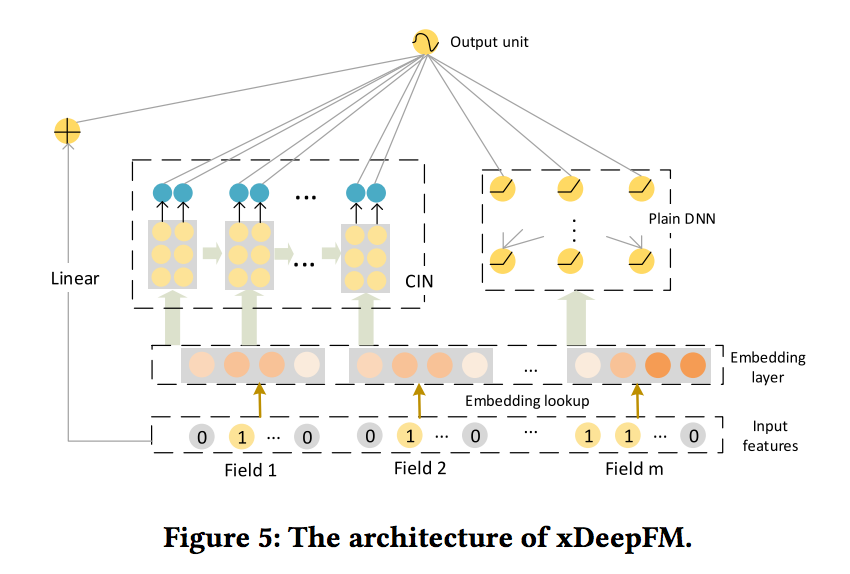
-> 이전의 DeepFM과의 차이점은 CIN부분이라 할 수 있다.

ABSTRACT

Combinatorial featrues은 많은 상용 모델의 성공에 필수적이다. -> 다만 직접 이러한 피처들을 제작하면 비용이 크다.
벡터곱의 관점에서의 Factorization based models은 피쳐들간의 패턴은 자동으로 학습하고 모이지 않는 특징으로 일반화 할 수 있다.
DNNs모델의 큰 성공으로, 최근 연구자들은 저차원 및 고차원의 특징의 상호 작용을 학습하기 위해 위해 몇몇 DNN 기반의 factorization 모델을 제안했다.
명시적인 방식으로 그리고 벡터 수준에서 특징적인 상호 작용을 생성하는 것을 목표로 하는 Novel Compressed Interaction Network(CIN)를 제안
CIN은 Convolutional Neural Network(CNN) 및 Recurrent Neural Network(RNN) 모델과 일부 기능을 공유함을 보여준다.
CIN과 클래식 DNN을 하나의 통합 모델로 결합하고 이 새로운 모델 eXtreme Deep Factorization Machine (xDeepFM) 라고 부른다.
xDeepFM은 bounded-degree도 기능 상호 작용을 학습할 수 있다. 반면, low- 와 high-order 피쳐의 상호작용을 학습 할 수 있습니다.

1 INTRODUCTION

feature은 많은 예측 시스템의 핵심적인 역할을 한다. raw features은 드물게 최적의 결과를 가져오기 때문에 데이터 과학자는 일반적으로 최상의 예측 시스템을 생성하거나 데이터마이닝을 위해 기능을 변환하는 데 많은 노력을 한다.
feature transformation의 유형 중 하나는 the cross-product transformation over categorical feature입니다. 이러한 피너는 cross features 또는 multi-way features이라 불리며 이들은 여러 raw feature을 상호작용을 측정한다.
기존의 교차 피쳐 엔지니어링에는 세가지 주요 단점
1. 높은 품질의 feature은 높은 비용이 든다.
1. web-scale 추천 시스템과 같은 큰 예측 시스템은 모든 교차 기능을 수동으로 추출할 수 없다.
2. hand-crafted 크로스 기능은 훈련 데이터에서 보이지 않는 상호 작용을 일반화하지 않는다.
Factorization Machines(FM)는 각 특징 i를 latent factor vector vi = [vi1, vi2, ..., viD]에 포함시키고 pairwise feature interactions은 잠재 벡터의 inner product으로 모델링된다 :
논문에서는 비트 벡터를 사용하여 잠재 벡터의 요소(FM)를 나타낸다.
classic FM은 arbitrary higher-order feature interactions으로 확장될 수 있지만, 한 가지 주요 단점은 모든 정보(유용하거나 유용하지 않거나)를 포함한다. ->이러한 features의 상호 작용으로 인해 노이즈가 발생하고 성능이 저하될 수 있다.
접근 방식은 DCN(Deep & Cross Network)을 기반으로 하며, 제한된 각도의 특징 상호 작용을 효율적으로 캡처하는 것을 목표로 합니다.
In this paper, we propose a neural network based model to learn feature interactions in an explicit, vector-wise fashion. -> 이 논문에서는, 신경망 기반 모델을 제안하며 explict, vector-wise fashion의 상호작용을 학습한다.
접근방식은 DCN(Deep & Cross Network)을 기반으로 하며, bounded degree의 특징 상호 작용을 효율적으로 포착하는 것을 목표로 한다.
그러나 2.3 장에서 DCN이 특별한 형식의 상호 작용으로 이어질 것이라고 주장할 것이다.
따라서 DCN의 교차 네트워크를 대체하기 위해 새로운 Compressed Interaction Network (CIN)를 설계한다.
CIN은 기능 상호 작용을 명시적으로 학습하고 상호 작용의 정도는 네트워크 깊이에 따라 증가한다.
Wide & Deep 및 DeepFM 모델을 따라, explicit high-order interaction module을 implicit interaction module과 전통적인 FM 모듈과 결합하고 joint model인 eXtreme Deep Factorization Machine(xDeepFM)라 부른다.

2 PRELIMINARIES

2.1 Embedding Layer

컴퓨터 비전이나 자연어 분야에서는 인풋데이터는 일반적으로 이미지 또는 텍스트 신호이다. -> raw data를 직접적으로 DNN을 적용할 수 있다.
web scale 추천 시스템에서 input data는 차원이 크고 sparse하기 때문에 (공간적 또는 시간적) 상관 관계가 명확하지 않다. -> 따라서 multi-field categorical form은 관련 작업에서 널리 사용된다.
아래의 이미지는 예시 input instance :
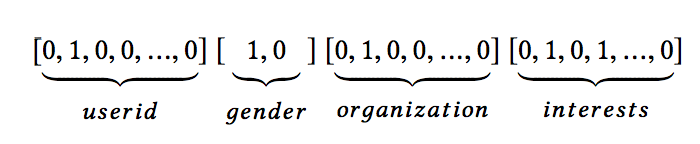
embedding layer은 row feature input에 적용되어 낮은 차원의 밀도가 높은 실수값 벡터로 압축한다.
- univalent(하나의 경우만 1이고 나머지는 0 : 위의 이지미에서 userid와 gender) -> 필드 임베딩으로 사용
- multivalent(univalent가 아닌경우 : 위의 이미지에서 organization과 interests)

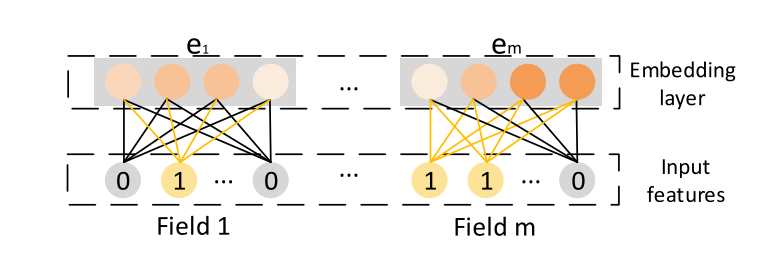
embedding layer의 결과는 넓게 연결된 벡터이다.
여기서 m은 필드 수를 나타내고 ei ∈ R^D는 하나의 필드를 포함한다.
인스턴스의 피처 길이는 다양할 수 있지만 임베딩의 길이는 m x D와 같다.(D : 필드 임베딩의 차원)

2.2 Implicit High-order Interactions

FNN, Deep Crossing, Wide & Deep의 deep 부분은 필드 임베딩 벡터 e에서 feed-forward neural network을 이용하여 고차원 특징 상호 작용을 학습한다.

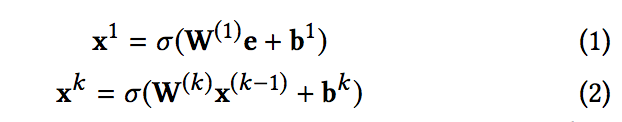
FM or Product Layer를 제외하고는 구조는 매우 유사합니다.(실제 xDeepFM은 DeepFM(아래 이미지)에서 FM구조가 CIN으로 변경된 것이다.)
이 아키텍처는 bit-wise fashion의 상호작용으로 모델링된다. 다시 말하면, 같은 필드안에 있는 요소는 필드 임베딩 벡터에 서로 영향을 미칩니다.
임베딩 벡터 e에 DNN을 적용하는 것 외에도 아키텍처에서 양방향 상호 작용 레이어를 추가한다. 따라서 비트 및 벡터와의 상호 작용이 모델에 포함된다.

2.3 Explicit High-order Interactions

high-order feature interaction을 명시적으로 모델링하는 것을 목표로 한다.
기존의 fully-connected feed-forward network와 달리, hidden layer은 다음과 같은 cross operation 의해 계산됨:

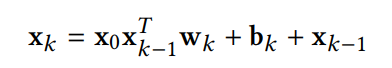
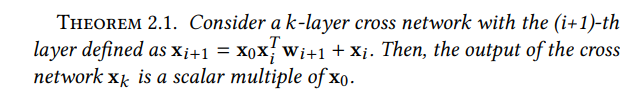
(증명 제외)

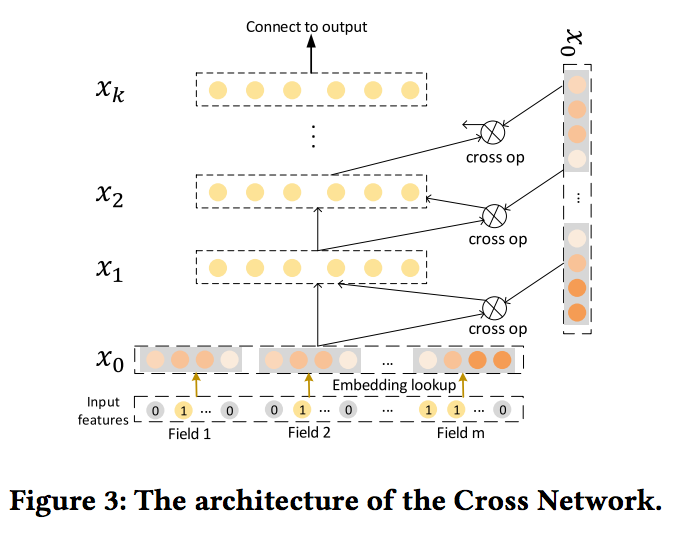
여기서 wk, bk, xk ∈ R^mD는 각 k 번째 층의 가중치, 바이어스 및 출력이다.
특징적인 상호 작용은 매우 효율적이며 (DNN 모델과 비교할 때 복잡성은 무시할 수 있음) 단점은 다음과 같다.
- (1) CrossNet의 출력은 특수한 형태로 제한되며, 각 숨겨진 레이어는 x0의 스칼라 배수이다.
- (2) 상호 작용은 비트 방식 (bit-wise fashion)으로 이뤄진다.

3 OUR PROPOSED MODEL

3.1 Compressed Interaction Network

Compressed Interaction이라는 새로운 cross network를 설계:
- (1) 상호 작용은 비트 단위가 아닌 벡터 단위로 적용
- (2) 고차원 특징 상호 작용이 명시적으로 측정
- (3) 네트워크의 복잡성은 상호 작용의 정도에 따라 기하 급수적으로 증가하지 않음
임베딩 벡터는 벡터와의 상호 작용을 위한 unit로 여겨지기 때문에 이후 필드 임베딩의 출력을 공식화한다.

(기타 특징 및 정보 생략)

각각의 layer에서, X^k는 아래의 수식으로 계산된다 :
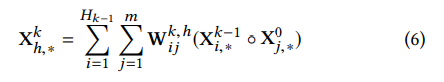
◦ : Hadamard product
(ex : ⟨a1, a2, a3⟩ ◦ ⟨b1, b2, b3⟩ = ⟨a1b1, a2b2, a3b3⟩)
Xk는 X^k-1과 X^0 사이의 상호 작용을 통해 도출되므로, 피처 상호 작용이 명시적으로 측정되고 상호 작용의 정도는 층 깊이에 따라 증가한다.
CIN의 구조는 RNN과 매우 유사하며 다음 은닉층의 출력은 마지막 은닉층과 추가 입력에 의존한다.(그림3처럼 연결되는 구조라 의존한다고 한다.)
모든 레이어에 벡터를 포함하는 구조를 유지하므로 상호 작용은 벡터 수준에서 적용됩니다.(기존의 DeepFM과 달리 그림 4처럼 계산과정을 통해 벡터를 유지하기 때문에 벡터 수준에서 적용된다고 한다.)
(6)의 식은 컴퓨터 비전에서 잘 알려진 CNN 과 밀접한 관련이 있다.

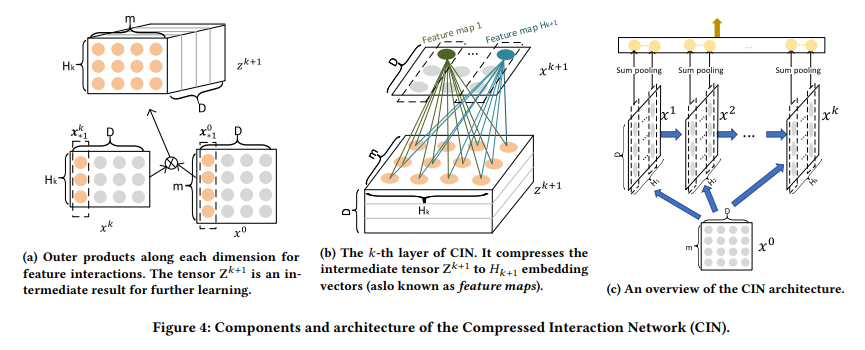
위의 그림 4(a)를 보면 중간 텐서 Z^(k+1)은 은닉층x^k 및 원래 특성 행렬 x⁰의 각 임베딩 차원을 따라있는 외부 곱다. 각 은닉층 x^k를 계산하는 과정은 컴퓨터 비전에서 잘 알려진 CNN과 밀접한 관련이 있다. 여기서 Z^(k+1)은 특별한 유형의 이미지로 볼 수 있으며 W^(k,h)는 필터이다.
그림 4(b)에서 볼 수 있듯이, 작성자는 임베딩 차원을 따라 Z^(k+1)을 가로 질러 필터를 밀어 넣고 숨겨진 벡터 x^(k+1)을 얻는다. 이는 일반적으로 컴퓨터 비전에서 feature map이라고 한니다. 따라서 x^k는 H_k 서로 다른 feature map의 모음이다.
그림 4(c)는 CIN의 아키텍처에 대한 개요를 제공한다. T는 네트워크의 깊이를 나타낸다. 모든 은닉층 X^k는 출력 단위와 연결되어 있다. 저자는 은닉층의 각 특징 맵에 합계 풀링을 적용하고 k 번째 은닉층에 대해 길이 H_k의 풀링 벡터 p^k를 얻는다. hidden layer의 모든 풀링 벡터는 출력 단위에 연결되기 전에 연결된다.