[Python] 머신러닝 완벽 가이드 # 10. 회귀 알고리즘

✏️ 10. 회귀 알고리즘

---

회귀(Regression) 개념

• 회귀는 현대 통계학을 이루는 큰 축

• 회귀 분석은 유전적 특성을 연구하던 영국의 통계학자 갈톤(Galton)이 수행한 연구에서 유래했다는 것이 일반론

  • “부모의 키가 크더라도 자식의 키가 대를 이어 무한정 커지지 않으며,
    부모의 키가 작더라도 대를 이어 자식의 키가 무한정 작아지지 않는다.”

• 회귀 분석은 이처럼 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법

회귀 개요

• 회귀는 여러 개의 독립변수(X)와 한 개의 종속변수(y) 간의 상관관계를 모델링하는 기법을 통칭한다.

• 𝑦 = 𝑓(𝑋)

  • 아파트 가격 < - > 방 개수, 아파트 크기, 주변 학군, 역과의 거리 등
𝑦 = 𝑤1𝑥1 + 𝑤2𝑥2 + 𝑤3𝑥3 + ⋯ + 𝑤𝑛𝑥𝑛

• 𝑦 는 종속변수, 즉 아파트 가격

• 𝑥1, 𝑥2, 𝑥3, ⋯ , 𝑥𝑛은 방 개수, 아파트 크기, 주변 학군, 역과의 거리 등 독립 변수

• 𝑤1, 𝑤2, 𝑤3, ⋯ , 𝑤𝑛은 이 독립 변수의 값에 영향을 미치는 회귀 계수(Regression Coefficients)

머신러닝 회귀 예측의 핵심은 주어진 Feature와 Target 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.

회귀 유형

• 회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러 가지 유형으로 나뉜다.

• 회귀에서 가장 중요한 것은 회귀 계수로서, 이 회귀 계수가 선형인지 아닌지에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다.

• 독립변수의 개수가 한 개인지 여러 개인지에 따라 단일 회귀, 다중 회귀로 나뉘게 된다.

• 정형 데이터의 경우 선형 회귀가 비선형 회귀보다 대부분의 경우 성능이 월등히 좋다.

독립변수 개수	회귀 계수의 결합
1개 : 단일 회귀	선형 : 선형 회귀
여러 개 : 다중 회귀	비선형 : 비선형 회귀

선형 회귀의 종류

• 일반 선형 회귀(LinearRegression)

  • 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며,
    규제(Regularization)를 적용하지 않은 모델

• 릿지(Ridge)

  • 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델

• 라쏘(Lasso)

  • 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식

• 엘라스틱넷(ElasticNet)

  • L2, L1 규제를 함께 결합한 모델

• 로지스틱 회귀(Logistic Regression)

  • 로지스틱 회귀는 회귀라는 이름이 붙어있지만, 사실은 분류에 사용되는 선형 모델

단순 선형 회귀(Simple Regression)을 통한 회귀의 이해

• 가격이 아파트 평수로만 결정 되는 단순 선형 회귀로 가정하면 다음과 같이 가격은 아파트 평수에 대해 선형(직선 형태)의 관계로 표현이 가능하다.

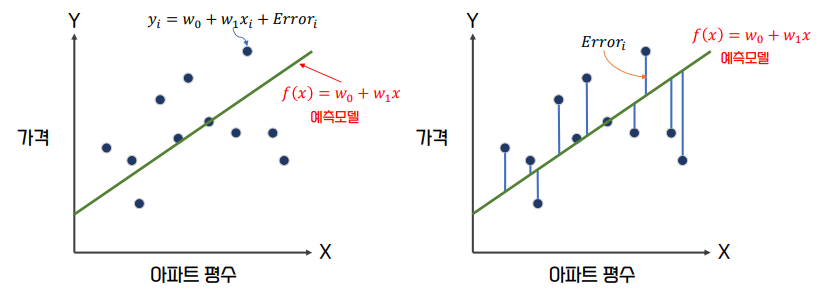
최적의 회귀 모델을 만든다는 것은 전체 데이터의 잔차(오류 값) 합이 최소가 되는 모델을 만든다는 의미이며 동시에 오류 값의 합이 최소가 될 수 있는 최적의 회귀 계수 w를 찾는다는 의미이다.

---

📌 참고 문헌

• 책

  • 📕 파이썬 머신러닝 완벽 가이드 / 권철민

• 해당 챕터의 실습 및 예제 코드는 아래 링크의 Machine Learning 참조 해주시면 됩니다.

  • ✍️ DataSci-Notes