
✏️ 11. RSS와 경사하강법
RSS 기반의 회귀 오류 측정
- RSS : 각 데이터 포인트의 오류 값(𝐸𝑟𝑟𝑜𝑟𝑖)의 제곱을 구해서 더하는 방식.
일반적으로 미분 등의 계산을 편리하게하기 위해서 RSS 방식으로 오류 합을 구한다.
즉, ∑𝐸𝑟𝑟𝑜𝑟2 = 𝑅𝑆𝑆 이다
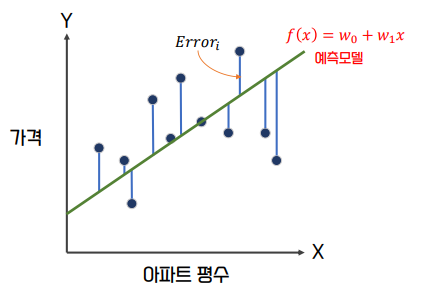
RSS의 이해
-
RSS는 이제 변수가 𝑤0, 𝑤1인 식으로 표현할 수 있으며, 이 RSS를 최소로 하는 회귀 계수(𝑤0, 𝑤1)를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심 사항
-
RSS는 회귀식의 독립변수 X, 종속변수 Y가 중심 변수가 아니라 회귀 계수 𝑤가 중심 변수임을 인지하는 것이 매우 중요하다.
-
학습 데이터로 입력되는 독립변수와 종속변수는 RSS에서 모두 상수로 간주
-
일반적으로 RSS는 학습 데이터의 건수로 나누어서 다음과 같이 정규화된 식으로 표현
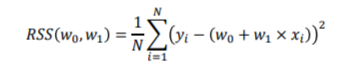
회귀의 비용 함수
-
회귀에서 RSS는 비용(Cost)이며 w 변수(회귀 계수)로 구성되는 RSS를 비용 함수(Cost Function)라 한다.
-
머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값(오류 값)을 지속해서 감소
-
최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것이 목적.
-
비용 함수를 손실함수(Loss Function)라고도 한다.
경사 하강법(Gradient Descent)
-
W 파라미터의 개수가 적다면 고차원 방정식으로 비용 함수가 최소가 되는 𝑤 변숫값을 도출할 수 있다.
-
하지만 𝑤 파라미터가 많다면 고차원 방정식을 동원하더라도 해결하기가 힘들다.
- 𝑤가 2개라면 이차방정식, 3개라면 삼차방정식… 100개면? 백차방정식이 된다.
-
경사 하강법은 이러한 고차원 방정식에 대한 문제를 해결해주면서 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식이다.
-
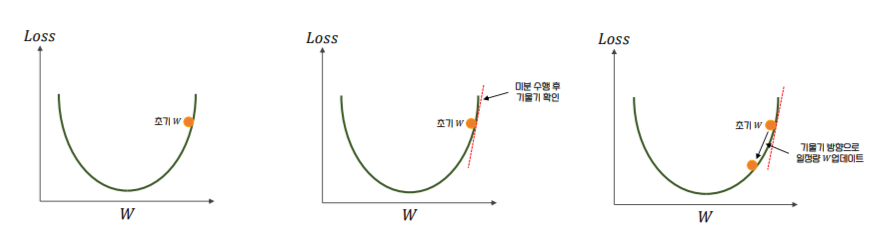
경사 하강법의 사전적 의미는 ‘점진적 하강’ 으로 ‘점진적으로’ 반복적인 계산을 통해 𝑊 파라미터 값을 업데이트 하면서 오류 값이 최소가 되는 𝑊 파라미터를 구하는 방식이다
-
경사 하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제값의 차이가 작아지는 방향성을 가지고 𝑊 파라미터를 지속해서 보정해 나간다.
-
최소 오류 값이 100이었다면 두 번째 오류 값은 100보다 작은 90, 세 번째는 80과 같은 방식으로 지속해서 오류를 감소시키는 방향으로 𝑊 파라미터 값을 계속 업데이트 해 나간다.
-
오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그 때의 𝑊 파라미터를 최적 파라미터로 반환한다.
미분을 통한 비용 함수의 최소값 찾기
- 어떻게 하면 오류가 작아지는 방향으로 𝑊 값을 보정할 수 있을까?
-
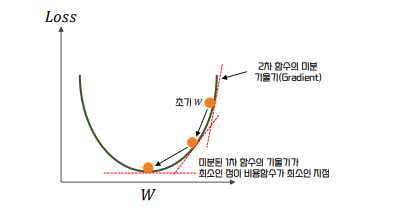
비용 함수가 다음 그림과 같은 포물선 형태의 2차함수라면 경사 하강법은 최초 𝑊 에서부터 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 𝑊 를 업데이트 한다.
-
마침내 더 이상 미분 된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그 때의 𝑊 를 반환한다.
📌 참고 문헌
-
책
- 📕 파이썬 머신러닝 완벽 가이드 / 권철민
-
해당 챕터의 실습 및 예제 코드는 아래 링크의 Machine Learning 참조 해주시면 됩니다.
