분류 모델의 성능 평가와 비교

지금까지 다양한 분류 방법들을 알아보았는데, 이 분류기의 성능을 어떻게 평가할 수 있을까?
단순하게 정확도를 보는 것도 방법이겠지만, 그 외에 여러가지 요소를 고려한 평가지표들을 살펴보자.

Confusion Matrix

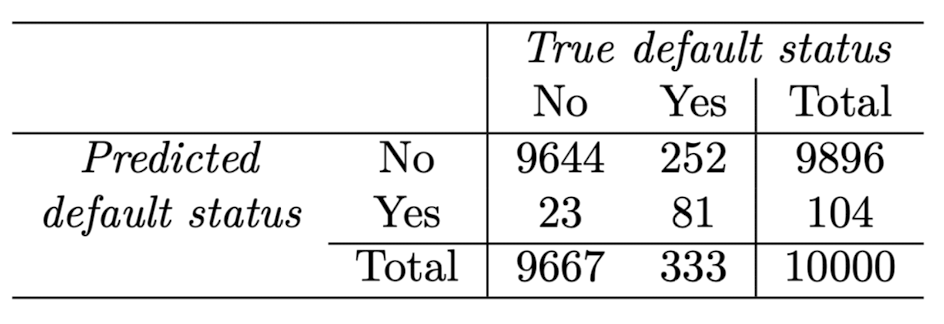
위 그림과 같은 표를 Confusion Matrix(혼동 행렬)이라고 한다. 이 표는 LDA를 이용해 카드값 연체 여부를 예측한 결과인데, LDA training error rate을 계산해보면 (23+252)/10000=0.0275로 2.57%이다.

그럼 Error rate(오분류율)이 낮다고 할 수 있는 걸까? 그렇지 않다.
Test error rate은 훨씬 더 클 것이고, 훈련 데이터의 연체 비율이 3.33%이므로 설령 모든 사람이 연체하지 않는다고 예측해도 Error rate는 3.33%이다.

혼동 행렬의 값들에 대해 알아보자.

• False positive(FP) = 23 : 실제로 No인 것을 Yes라고 판단
  통계적으로는 '귀무가설이 참임에도 불구하고 귀무가설을 기각하는 오류'로, 제 1종 오류 라고도 한다.
  제 1종 오류 발생 확률($\alpha$) = 23 / 104

• False Negative(FN) = 252 : 실제로 Yes인 것을 No이라고 판단
  통계적으로는 '귀무가설이 거짓임에도 불구하고 귀무가설을 채택하는 오류'로, 제 2종 오류 라고도 한다.
  제 2종 오류 발생 확률($\beta$) = 252 / 9896

• True Negative(TN) = 9644 : 실제로 No인 것을 No라고 판단
  Specificity(특이도) : 실제 False인 사례 중 False로 분류한 비율 = 9644 / 9667 = 99.9%

• True Positive(TP) = 81 : 실제로 Yes인 것을 Yes라고 판단
  Sensitivity(민감도) : 실제로 True인 사례 중 제대로 True로 분류한 비율 = 81 / 333 = 24.3%

클래스 분류 성능은 의료 분야에서 중요한데, 여기서 Sensitivity와 Specificity로 분류기나 검사의 성능을 나타낸다. 하지만 대부분의 문제에서 Positive를 옳게 판별하는 것에 관심이 있고 Negative를 옳게 판별하는 것에는 큰 관심이 없다.
따라서 Sensitivity를 높여야 하는데, 그를 위해 positive로 판정하는 기준을 낮출 필요가 있다.

현재 연체자를 분류하는 기준은

인데, 0.2 이상으로 임곗값을 낮추어

로 설정해보자.

위 기준을 바탕으로 예측한 Confusion Matrix는 다음과 같다,

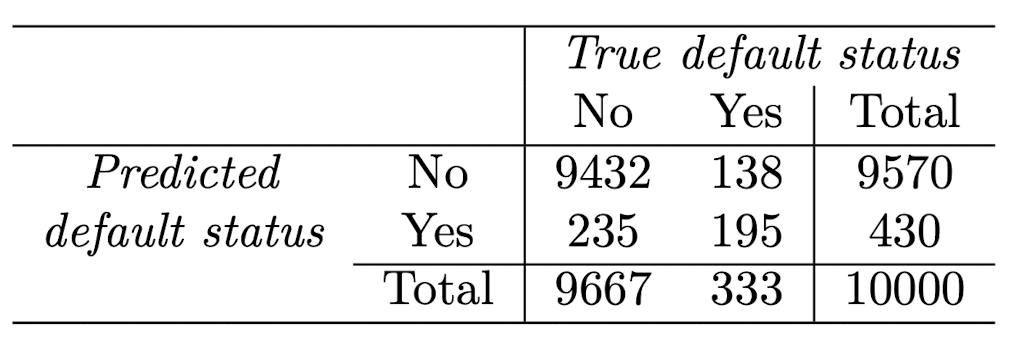
그리고 민감도를 계산해보면 195 / 333 = 58.6%로 연체자를 41.4% 못 맞추고, 특이도는 9432 / 9667 = 97.6%로 비연체자를 2.5% 못 맞춘다.
비연체자를 오분류하는 경우는 크게 신경쓰지 않으므로 특이도가 좀 커져도 괜찮다.

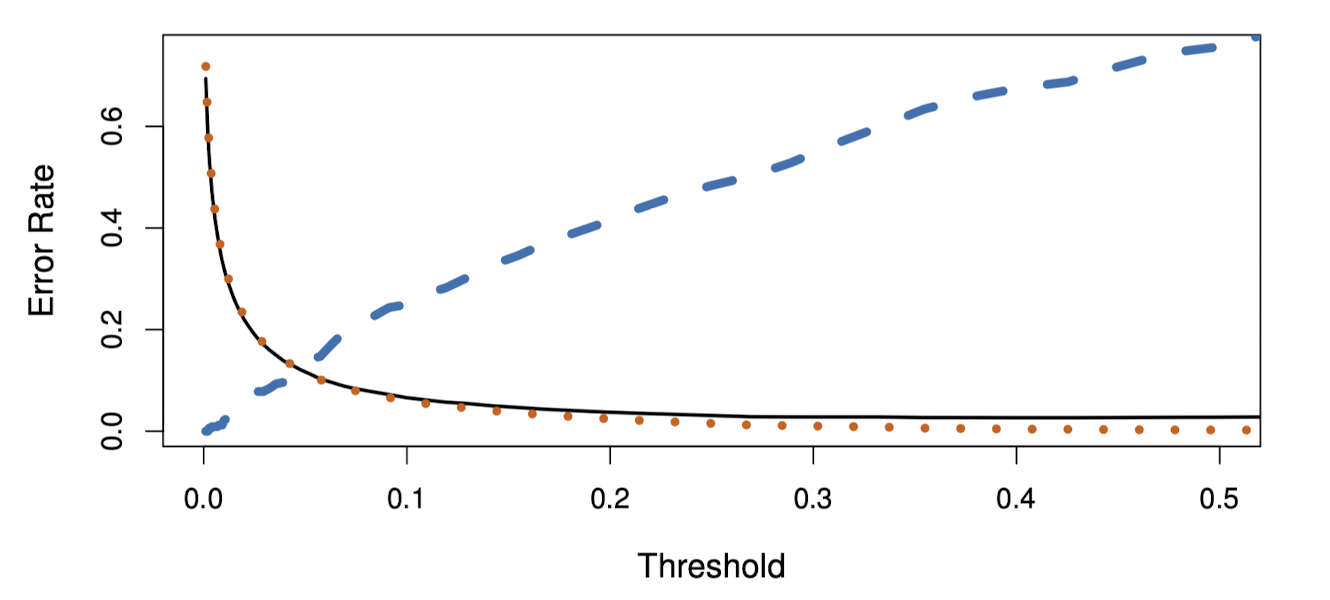
위 그림에서 파란색 점선은 (1-Sensitivity)로 연체자들 중 오분류된 비율, 주황색 점선은 (1-Specificity)로 비연체자들 중 오분류된 비율이다.

ROC Curve

ROC Curve는 Receiver Operating Characteristic Curve의 약자이다. 서로 다른 분류 모델의 성능을 비교할 때 유용하며, 가능한 모든 Threshold을 고려한다.

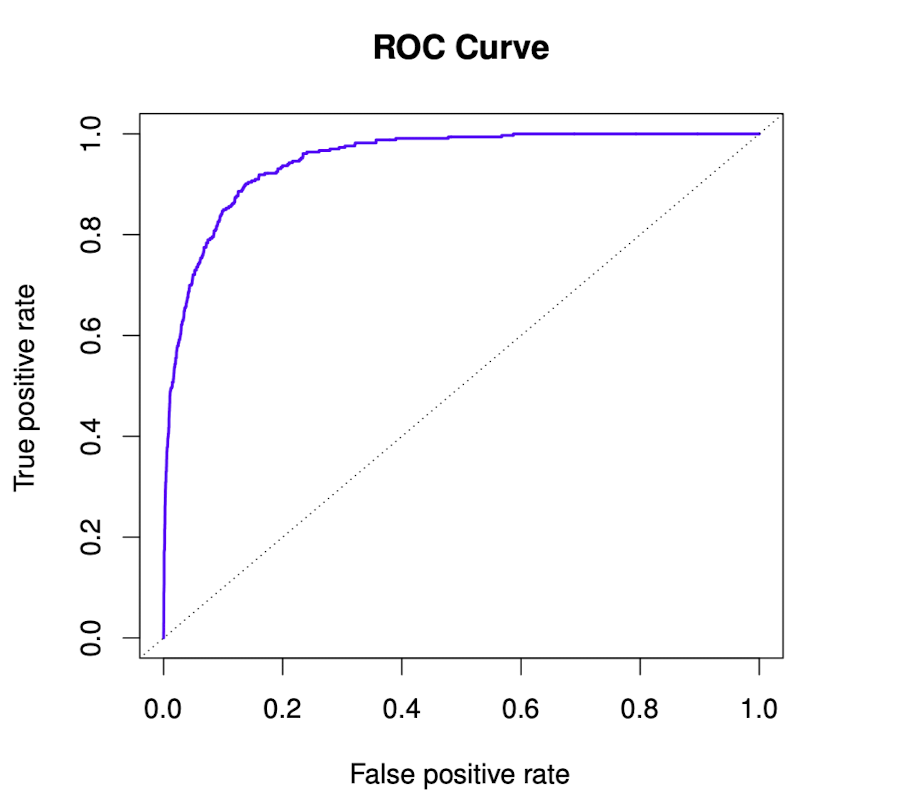
Y축은 TPR로, Sensitivity와 같은 값이며 X축은 FPR로 1-Specificity와 같다.
분류 모델의 성능은 ROC 곡선 아래의 면적(AUC : Area Under the Curve)에 의해 결정되는데,
AUC가 클수록 좋은 분류기가 된다.

Comparisons of Four Classification Methods

지금까지 다루었던 분류 모델은 로지스틱 회귀, LDA, QDA, Naive Bayes, KNN이 있다.

각 모델 간의 비교를 한번 해보자.

Logistic Regression vs LDA (K=2, p=1)

$p_1(x),\ p_2(x)=1-p_1(x)$ : 관측치 $X=x$이 클래스 1과 2로 분류될 확률
Logistic Regression : $log\frac{p_1}{1-p_2}=\beta_0+\beta_1x$
LDA : $log\frac{p_1}{1-p_2}=c_0+c_1x$

두 모델이 모두 선형 함수이므로, linear decision boundary를 만든다는 것을 알 수 있다. 로지스틱 회귀 모델의 $\beta_0, \beta_1$은 MLE를, $c_0,c_1$은 정규 분포에서 추정된 평균과 분산으로 구하면 된다.

만약 각 클래스들이 공통 공분산 행렬을 갖는 경우에는 LDA가 우수한 성능을 보인다. 하지만 밀도 함수가 정규 분포라는 것을 가정할 수 없다면 로지스틱 회귀가 더 우수한 성능을 갖는다.

KNN vs Logistic Regression or LDA

KNN은 비모수적 방법으로, 베이즈 정리를 기반으로 한 모델들과 다르게 결정 경계에 대해 어떠한 가정도 필요로 하지 않는다는 특징이 있다.
따라서 결정 경계가 매우 비선형적라면 KNN이 LDA나 Logistic Regression보다 더 우수하다.

KNN은 정확한 분류를 위해 예측 변수의 수에 비해 많은 관측값이 필요하다. 즉, $n$이 $p$ 보다 훨씬 커야 한다. 비모수적이기에 편향을 줄이지만, 그만큼 분산이 커지기 때문이다.

마지막으로 해석이 어렵다는 단점이 있다.

QDA vs Others

QDA는 KNN과 LDA and Logistic Regression의 절충안이라고 할 수 있다.
KNN만큼 유연하지는 않지만, 비선형 결정 경계를 가지면서도 모수적 방법을 사용하기 때문에 관측값이 적을 경우 KNN보다 더 정확하게 분류가 가능하다.

Naive bayes vs Others

나이브 베이즈는 예측 변수들 간 상관관계가 없고 밀도 함수가 정규분포를 따를 때 성능이 우수하다. 특히 Sample size $n$에 비해 예측 변수의 개수 $p$가 클 때 유용하다.

Simulation Studies

이제 각 분류기들의 실질적인 성능을 비교해보자. 6가지 다른 시나리오들에서 데이터를 생성했으며,
각각 이진 분류 문제를 다루고 있다.
시나리오 1~3은 베이즈 결정 경계가 선형이고, 시나리오 4~6에서는 비선형이다.

각 시나리오에서 100개의 랜덤 훈련 데이터 셋을 생성했고 각 분류 방법의 Test Error rate를 계산하여 박스플롯으로 나타냈다.

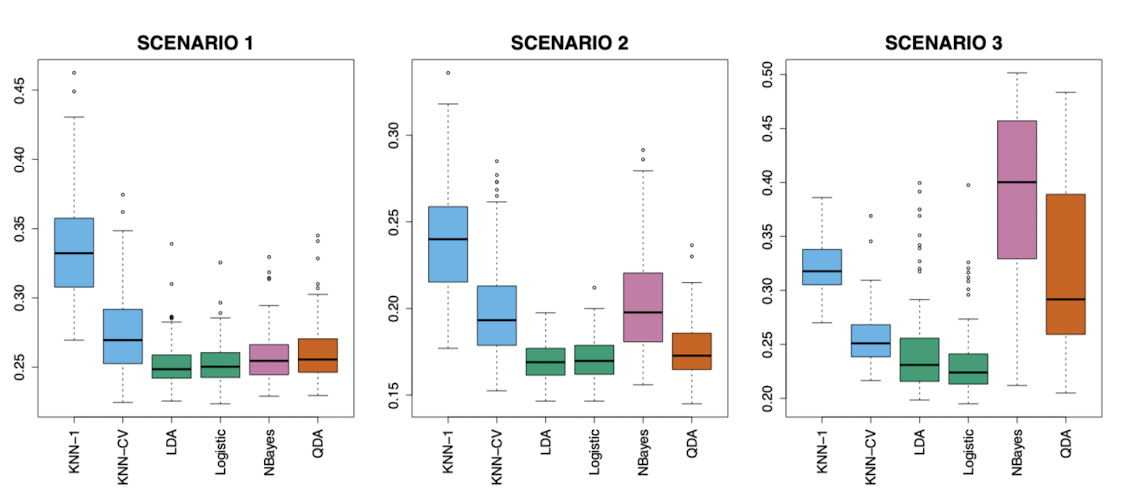
• 시나리오 1 : N=20, K=2, P=2, 클래스 별 평균 다름, 관측치는 서로 상관되지 않은 정규 분포 변수
  위 조건이 LDA에 적합하므로 LDA의 오분류율이 가장 낮다. 그리고 그와 비슷한 경계를 갖는 Logistic Regression 역시 좋은 성능을 보이고 있다.
  QDA는 필요 이상으로 유연하게 작용했기 때문에 LDA 보다 약간 낮은 성능을 갖으며, 비슷하지만 관측값들이 서로 독립적이고 정규분포를 만족한다는 가정이 있기 때문에 QDA 보다 약간 나은 성능을 보여준다.

• 시나리오 2 : 세부 사항은 시나리오 1과 동일하나 두 예측 변수가 -0.5의 상관관계
  시나리오 1과 거의 비슷하지만 예측변수 간 독립성이 위배되기 때문에 나이브 베이즈의 성능이 떨어졌다.

• 시나리오 3 : 시나리오 2와 비슷하게 예측변수 간 큰 음의 상관관계가 있고, 관측값들이 정규 분포를 따르지 않음.
  예측변수의 독립성 가정과 정규 분포 가정을 만족하지 않으나 결정 경계가 여전히 선형이었으므로 Logistic Regression이 가장 좋은 성능을 보였다.
  따라서 LDA에 약간의 성능 저하가 있었고 QDA와 나이브 베이즈는 큰 성능 저하가 발생했다.

• 시나리오 4 : 클래스 1에서는 예측변수 간 상관계수가 0.5, 클래스 2에서는 -0.5인 정규 분포에서 데이터가 생성됨
  위 조건에 QDA가 가장 부합하며, 결과적으로 이차 결정 경계가 만들어졌다.
• 시나리오 5 : 예측변수 간 상관관계가 없고, 설명 변수가 비선형 함수로부터 추출됨.
  데이터가 복잡한 비선형 관계를 갖기 때문에 선형 방법보다 QDA와 나이브 베이즈가 약간 나은 성능을 보였고, 유연한 KNN-CV가 높은 성능을 보인다.
  K=1은 필요 이상으로 복잡한 경계를 갖기 때문에 적절한 K값의 선택이 중요하다는 것을 알 수 있다.
• 시나리오 6 : 클래스 별로 다른 공분산 행렬을 갖는 정규분포에서 데이터가 생성됨. 샘플 크기가 n=6으로 매우 작음
  나이브 베이즈 가정이 만족되어 매우 좋은 성능을 보였지만 KNN은 너무 작은 샘플 크기 때문에 비교적 성능이 저조했다.
  LDA와 Logistic Regression은 비선형 경계를 갖지 않아 성능이 저조했다.
  QDA는 예측변수 간 상관관계를 추정하는데 너무나 큰 분산을 초래해 나이브 베이즈보다 성능이 떨어졌다.

결론적으로
1. 하나의 방법이 반드시 다른 방법보다 우월하지 않다.
2. 결정 경계가 선형일 때는 LDA와 Logistic Regression이, 비선형일 때는 QDA와 나이브 베이즈가 더 나을 수 있다.
3. 복잡한 결정 경계에서는 일반적으로 KNN의 성능이 좋지만, K값을 적절히 선택해야 한다.
라는 것을 알 수 있다.