[R] Resampling

sunnyboy·2024년 10월 18일

R cross validation

Data Mining

목록 보기

6/9

Cross Validation

Test Error Rate를 추정할 때 사용할 수 있는 Test Data가 없다면 어떻게 해야할까?

훈련 데이터셋 중 일부를 제외하고 모형을 적합한 뒤, 제외된 관측치들을 테스트 데이터셋처럼 적용하여
Test Error Rate를 추정할 수 있는 방법을 소개한다.

Validation Set Approach

Validation Set Approach의 절차에 대해 알아보자.

관측치들을 임의로 Training Set과 Validation Set로 나눈다.
Training Set을 가지고 모델을 적합한 뒤 Validation Set의 관측치를 적합된 모델에 대입하여 예측값을 얻는다.
Validation Set의 Response값과 예측값을 비교하여 Test Error Rate를 계산한다.(연속형 변수인 경우 MSE)

아래와 같은 단점도 존재한다.
1. Training Set과 Validation Set에 포함된 관측값에 따라 변동이 심함.
2. 관측값이 적을수록 성능이 나빠짐. >> Test Error Rate이 과대 추정됨.

ISLR 라이브러리의 Auto 데이터셋으로 Validation Set Approach을 구현해보자.

> library(ISLR)
> set.seed(1)
> train = sort(sample(1:392, 196))
> test = setdiff(1:392, train)
> lm.fit = lm(mpg ~ horsepower, data = Auto, subset = train)
> summary(lm.fit)

Call:
lm(formula = mpg ~ horsepower, data = Auto, subset = train)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.3177 -3.5428 -0.5591  2.3910 14.6836 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 41.283548   1.044352   39.53   <2e-16 ***
horsepower  -0.169659   0.009556  -17.75   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.032 on 194 degrees of freedom
Multiple R-squared:  0.619,	Adjusted R-squared:  0.6171 
F-statistic: 315.2 on 1 and 194 DF,  p-value: < 2.2e-16

> yhat = predict(lm.fit, newdata = Auto[test,])
> mean((Auto$mpg[test] - yhat)^2) # Test MSE
[1] 23.26601

2차, 3차 모형도 적합하여 Test MSE를 비교해보자.

> # degree of 2
> lm2.fit = lm(mpg ~ poly(horsepower, 2), data = Auto, subset = train)
> yhat = predict(lm2.fit, newdata = Auto[test,])
> mean((Auto$mpg[test] - yhat)^2) # Test MSE
[1] 18.71646
> # degree of 3
> lm3.fit = lm(mpg ~ poly(horsepower, 3), data = Auto, subset = train)
> yhat = predict(lm3.fit, newdata = Auto[test,])
> mean((Auto$mpg[test] - yhat)^2) # Test MSE
[1] 18.79401

이 Training Set에서는 2차 모형을 사용하는 것이 가장 좋은 성능을 갖는다.

LOOCV (Leave-One-Out Cross-Validation)

하나의 관측치 $(x_i,y_i)$ 를 Validation Set으로, 나머지 관측치 ${(x_1,y_1),..., (x_{i-1},y_{i-1}),(x_{i+1},y_{i+1}),...,(x_n,y_n)}$ 들을 Training Set으로 사용.
모델은 n-1개의 Training Set 관측치로 적합하고 $x_i$ 를 적합된 모델에 대입하여 관측값 $(\hat y_i)$ 추정.
이 과정을 n번 반복하여 $\hat y_1,...,\hat y_n$ 을 추정하고 Test MSE를 계산. $MSE_{test}=\frac{1}{n}\sum_{i=1}^n(y_i-\hat y_i)^2$

LOOCV의 장점으로는
1. Validation Set Approach에 비해 편향이 훨씬 적다.
2. Test Error Rate을 과대 추정하지 않음 >> Test Data를 거의 다 썼기 때문.
3. 여러 번 적용해도 항상 동일한 Test MSE를 얻음.

단점은 계산하는데에 시간이 오래걸릴 수 있다는 것이다.

LOOCV를 Auto 데이터셋으로 구현해보자.

> glm.fit = glm(mpg ~ horsepower, data = Auto)
> summary(glm.fit)

Call:
glm(formula = mpg ~ horsepower, data = Auto)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 39.935861   0.717499   55.66   <2e-16 ***
horsepower  -0.157845   0.006446  -24.49   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for gaussian family taken to be 24.06645)

    Null deviance: 23819.0  on 391  degrees of freedom
Residual deviance:  9385.9  on 390  degrees of freedom
AIC: 2363.3

Number of Fisher Scoring iterations: 2

> library(boot)
> cv.err = cv.glm(Auto, glm.fit)
> cv.err$delta # MSE of parameter (mpg, horsepower)
[1] 24.23151 24.23114

delta의 값들 중 첫 번째는 일반적인 예측값이고, 두 번째는 편향 보정이 된 예측값이다.
일반적으로 두 값이 비슷하기 때문에 첫 번째 값을 사용하면 된다.

이번에는 1차부터 5차 회귀모형을 적합해 교차검증을 실시해보자.

> cv.error = rep(0, 5)
> for (i in 1:5){
+   glm.fit = glm(mpg ~ poly(horsepower, i), data = Auto)
+   cv.error[i] = cv.glm(Auto, glm.fit, K = 10)$delta[1]
+ }
> cv.error
[1] 24.18591 19.25879 19.13253 19.52528 18.84753

선형 모형에서 2차 모형 사이에는 추정된 Test Error가 크게 감소하지만, 그 이후부터는 뚜렷한 차이를 보이지는 못하고 있다.

K-fold CV

관측치 데이터셋을 임의로 크기가 거의 같은 k개의 fold로 분할하여 하나의 fold는
Validation Set으로 사용하고 나머지 k-1개의 folds는 Training Set으로 사용.
모델은 Training Set으로 지정한 k-1개의 folds를 가지고 적합한 뒤, 남은 Validation Set의 관측치를 모델에 대입하여 예측값을 얻음.
이 과정을 k회 반복하여 $\hat y_1,...,\hat y_n$ 을 추정하고 Test MSE를 계산.

일반적으로 k=5 혹은 k=10으로 설정한다.

K-fold CV의 장점으로는
1. n번이 아니라 k번 모델을 적합하므로 LOOCV보다 계산이 효율적임.
2. LOOCV에 비해 Test Error Rate에 대한 정확한 추정이 가능함.

K-fold CV 가 더 정확한 추정치를 제공하는 것은 Bias-Varianve Trade-Off와 관련이 있다.
LOOCV는 각 Training Set에 n-1개의 관측값을 포함하므로 추정치에 대한 편향이 거의 없다는 것을 알 수 있다. 반면 K-fold CV는 Training Set에 적은 관측값을 포함하므로 약간의 편향이 있을 것이다. 따라서 편향 감소의 관점에서 볼 때 LOOCV가 K-fold CV보다 좋은 방법임이 분명하다.

하지만 편향뿐만 아니라 분산도 고려해야 하는데, LOOCV는 K-fold CV에 비해 더 높은 분산을 가지게 된다. 그 이유는 LOOCV에서 거의 동일한 Training Set으로 모델을 적합한다. 각 모델들이 강한 상관관계를 갖게 되는 것인데, 서로 강하게 상관된 모델로부터 얻은 추정치는 비교적 더 높은 분산을 갖는 경향이 있다.

즉, K-fold CV에서 k값에 따른 Bias-Varianve Trade-Off가 존재한다. 통상적으로 k=5나 k=10을 사용하는데, 이 값들은 너무 높은 편향이나 분산을 갖지 않는 Test Error Rate 추정치를 제공한다는 것이 알려져 있다.

K-fold CV도 R로 구현해보자.

> set.seed(17)
> cv.error_10 = rep(0, 10)
> for (i in 1:10) {
+   glm.fit = glm(mpg ~ poly(horsepower, i), data = Auto)
+   cv.error_10[i] = cv.glm(Auto, glm.fit, K=10)$delta[1]
+ }
> cv.error_10
 [1] 24.27207 19.26909 19.34805 19.29496 19.03198 18.89781 19.12061 19.14666 18.87013 20.95520

K-fold CV에서도 LOOCV와 마찬가지로, 선형 모형에서 이차 모형로 넘어갈 때는 큰 차이가 있지만 그 이후부터는 뚜렷한 차이가 없다.

Cross-Validation for Classification

앞서 반응변수 $Y$ 가 연속형 변수인 경우에 대해서 다루었다. 하지만 교차검증은 $Y$ 가 범주형 변수인 경우에도 유용한 방법이 된다. 단, MSE가 아닌 아래와 같은 값을 사용한다.

LOOCV for Classification $Err_{test} = \frac{1}{n}\sum_{i=1}^n Err_i,\quad Err_i=I(y_i\neq\hat y_i)$

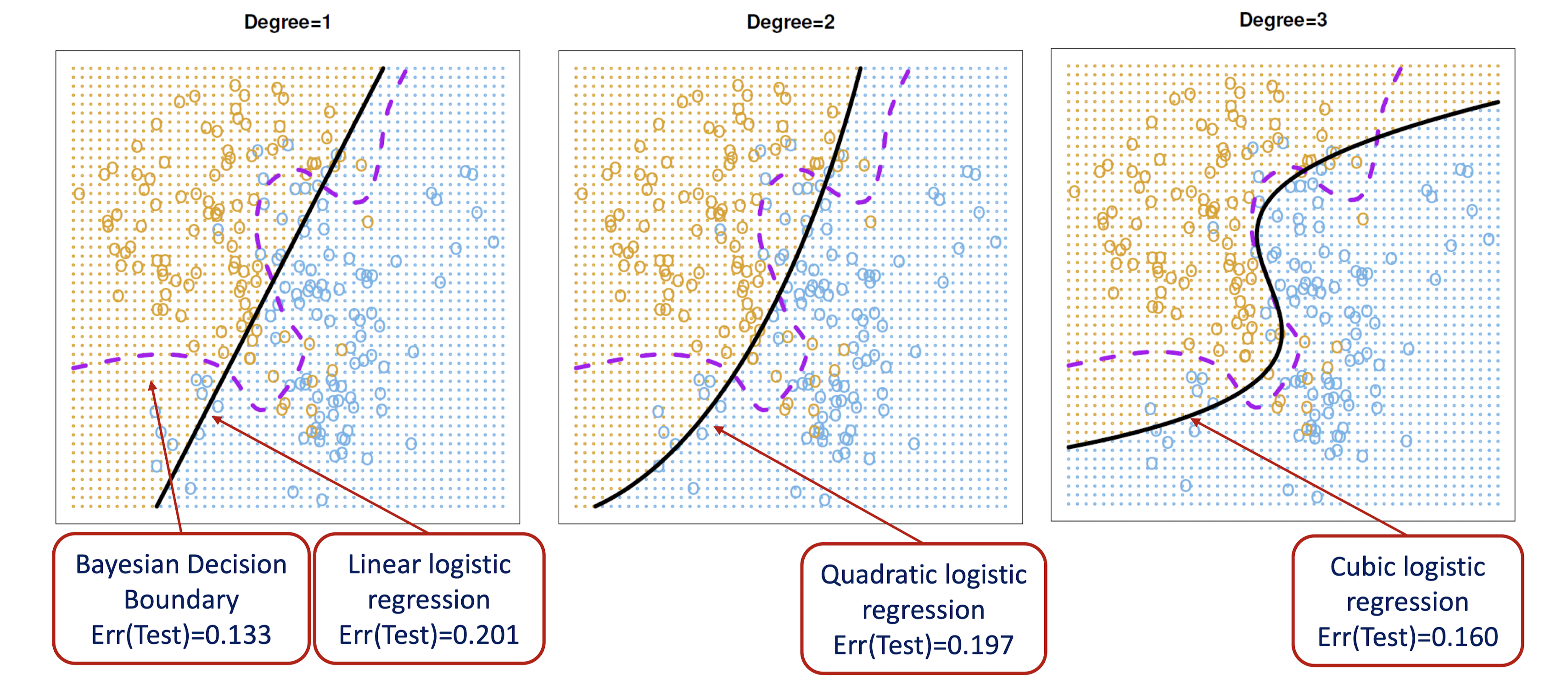
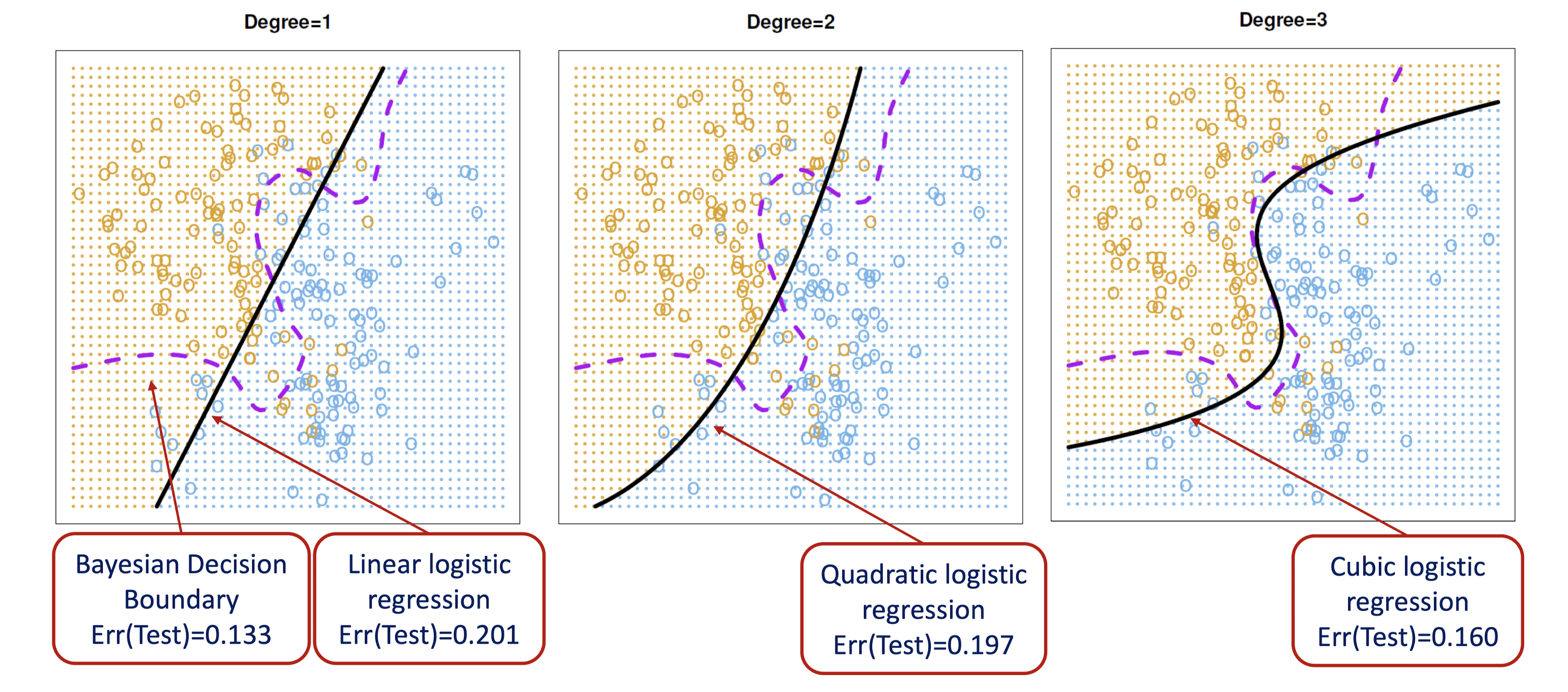
아래 그림은 각각 1차, 2차, 3차 logistic regression으로 생성한 결정경계를 베이즈 결정경계와 함께 나타낸 것이다. 3차항을 포함한 모형에서 가장 높은 성능을 보이고 있다.

아래 왼쪽 그림에서 검은색 선은 10-fold CV Error를 나타낸 그래프인데, 4차항을 포함한 logistic regression을 사용할 때 가장 낮은 오류율을 보인다.
실제 Test Error가 3차항일 때 최소라는 점을 고려하면 어느 정도 비슷한 값이라고 볼 수 있다.

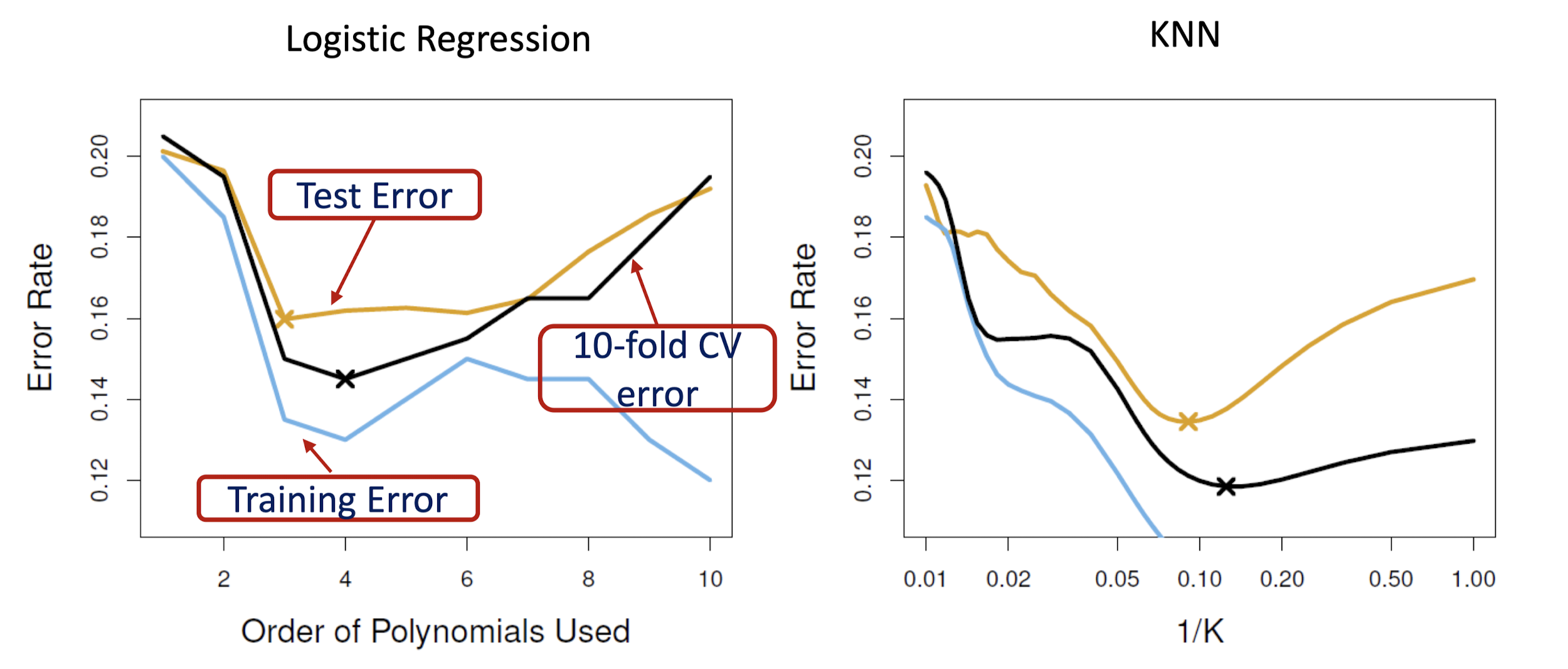
오른쪽 그림에서도 Test Error와 유사한 K값을 보인다. 하지만 실제 데이터에서는 Test Error를 알 수 없다.
10-fold CV는 Test Error를 과소추정하는 경향이 있긴 하지만 다항식의 차수나 K값은 유사하게 추정하므로 괜찮은 방법이다.

Bootstrap

$n$ 개의 관측치를 포함하는 $Z$ 라는 데이터 셋이 있다고 하자.
$Z$ 에서 복원 추출로 데이터 셋을 만드는 과정을 B번 수행하여 $Z_1^*,Z_2^*,...Z_B^*$ 라는 B개의 데이터셋을 만든다. 이 데이터셋에는 $Z$ 의 동일한 관측치가 두 번 이상 포함될 수 있고, 사이즈는 $Z$ 와 같다.

이때 $Z_1^*,Z_2^*,...Z_B^*$ 를 Boostrap Data Set이라고 한다.
이 부스트랩 데이터 셋에 대응하는 통계량 $\hat\alpha_1^*,\hat\alpha_2^*,...,\hat\alpha_B^*$ 을 추정한다면, 표준오차를 구해 추정값의 변동성을 추정할 수 있다.

SE_B(\hat\alpha) = \sqrt{\frac{1}{B-1}\sum_{r=1}^B(\hat{\alpha_r^*}-\bar{\alpha^*})^2},\quad \bar{\alpha^*}=\frac{1}{B}\sum_{r'=1}^B\hat{\alpha_{r'}^*}

이제 부스트랩 현실에서 적용할 수 있는 예를 하나 들어보겠다.

금융자산 X와 Y에 고정된 금액을 투자한다고 가정하자. 우리는 전체 자금 중 $\alpha$ 만큼을 X에 투자하고, $1-\alpha$ 만큼을 Y에 투자할 것이다.

이때 두 자산의 수입에는 변동이 있기 때문에 총 투자에 따른 위험을 최소화하는 $\alpha$ 를 결정해야 한다.
즉, 우린 $Var(\alpha X + (1-\alpha)Y)$ 를 최소화하고 싶다. $\alpha$ 를 다음과 같이 표현된다.

\alpha = \frac{\sigma_Y^2-\sigma_{XY}}{\sigma_X^2+\sigma_Y^2-2\sigma_{XY}}

ISLR 라이브러리의 Portfolio 데이터 셋을 이용하여 $\alpha$ 를 추정해보자.
우선 부스트랩이 아닌 기본 데이터셋 전체를 이용한 추정치를 구해보겠다.

> head(Portfolio)
           X          Y
1 -0.8952509 -0.2349235
2 -1.5624543 -0.8851760
3 -0.4170899  0.2718880
4  1.0443557 -0.7341975
5 -0.3155684  0.8419834
6 -1.7371238 -2.0371910
> alpha.fn = function(data, index) {
+   X = data$X[index]
+   Y = data$Y[index]
+   
+   (var(Y) - cov(X, Y)) / (var(X) + var(Y) - 2*cov(X, Y))
+ }
> alpha.fn(Portfolio, 1:100)
[1] 0.5758321

이번에는 전체 데이터셋에서 복원 추출을 허용하여 만든 데이터셋으로 추정치를 구해보겠다.

> alpha.fn(Portfolio, sample(1:100, 100, replace = TRUE))
[1] 0.5035355
> length(table(sort(sample(1:100, 100, replace = TRUE))))
[1] 61

이제 부스트랩 방법으로 추정치를 구해보자. 총 1000개의 데이터셋을 생성하겠다.

> library(boot)
> boot(Portfolio, alpha.fn, R=1000)

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = Portfolio, statistic = alpha.fn, R = 1000)


Bootstrap Statistics :
     original       bias    std. error
t1* 0.5758321 -0.003259533  0.09365668

구한 추정치 $\hat\alpha$ 는 0.5758321, 표준오차는 0.093 이다.

이제 앞서 Auto 데이터 셋에서 적합한 선형 모형의 회귀 계수 추정량을 부스트랩을 이용해 구해보자.
처음부터 순서대로 전체 데이터 셋, 복원 추출로 만든 데이터 셋, 부스트랩 데이터 셋을 사용해 추정했다.

> boot.fn = function(data, index) {
+   result = coef(lm(mpg ~ horsepower, data = data, subset = index))
+   return(result)
+ }
> boot.fn(Auto, 1:392)
(Intercept)  horsepower 
 39.9358610  -0.1578447 
> boot.fn(Auto, sample(1:392, 392, replace = TRUE))
(Intercept)  horsepower 
 39.5081551  -0.1548261 
> boot(Auto, boot.fn, R=1000)

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = Auto, statistic = boot.fn, R = 1000)


Bootstrap Statistics :
      original        bias    std. error
t1* 39.9358610  0.0532283200 0.858706987
t2* -0.1578447 -0.0005468276 0.007345117

부스트랩으로 구한 Std.Error와 summary()의 Std.Error를 비교하면 차이가 있다.

> summary(lm(mpg ~ horsepower, data = Auto))$coef
              Estimate  Std. Error   t value      Pr(>|t|)
(Intercept) 39.9358610 0.717498656  55.65984 1.220362e-187
horsepower  -0.1578447 0.006445501 -24.48914  7.031989e-81

선형 회귀모형은 여러 가정에 의존하고 있는데, 부스트랩은 어떤 가정들을 필요로 하지 않으므로
부스트랩 방법이 더 정확하게 추정하고 있다고 볼 수 있다.

이제 이차 회귀모형의 계수도 추정해보자.

> boot2.fn = function(data, index) {
+   result = coef(lm(mpg ~ poly(horsepower, 2, raw = T), data = data, subset = index))
+   return(result)
+ } 
> boot2.fn(Auto, 1:392)
                  (Intercept) poly(horsepower, 2, raw = T)1 poly(horsepower, 2, raw = T)2 
                 56.900099702                  -0.466189630                   0.001230536 
> boot2.fn(Auto, sample(1:392, 392, replace = TRUE))
                  (Intercept) poly(horsepower, 2, raw = T)1 poly(horsepower, 2, raw = T)2 
                  60.59668719                   -0.52200066                    0.00142021 
> boot(Auto, boot2.fn, R=1000)

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = Auto, statistic = boot2.fn, R = 1000)


Bootstrap Statistics :
        original        bias     std. error
t1* 56.900099702  1.020497e-01 2.1397048133
t2* -0.466189630 -2.059071e-03 0.0343076804
t3*  0.001230536  8.649654e-06 0.0001242662
> summary(lm(mpg ~ poly(horsepower,2,raw = T), data = Auto))$coef
                                  Estimate   Std. Error   t value      Pr(>|t|)
(Intercept)                   56.900099702 1.8004268063  31.60367 1.740911e-109
poly(horsepower, 2, raw = T)1 -0.466189630 0.0311246171 -14.97816  2.289429e-40
poly(horsepower, 2, raw = T)2  0.001230536 0.0001220759  10.08009  2.196340e-21

sunnyboy

Data Analysis, ML, Backend 이것저것 합니다

이전 포스트

분류 모델의 성능 평가와 비교

다음 포스트