[R] KNN

K-Nearest Neighbors (KNN)

또 다른 클래스 분류 방법 K-최근접 이웃(K-Nearest Neighbors : KNN)에 대해 소개하겠다.

주어진 $X$에 대한 $Y$의 조건부 분포를 추정하여 가장 높은 추정확률을 가지는 클래스로 분류하는 방법이다.

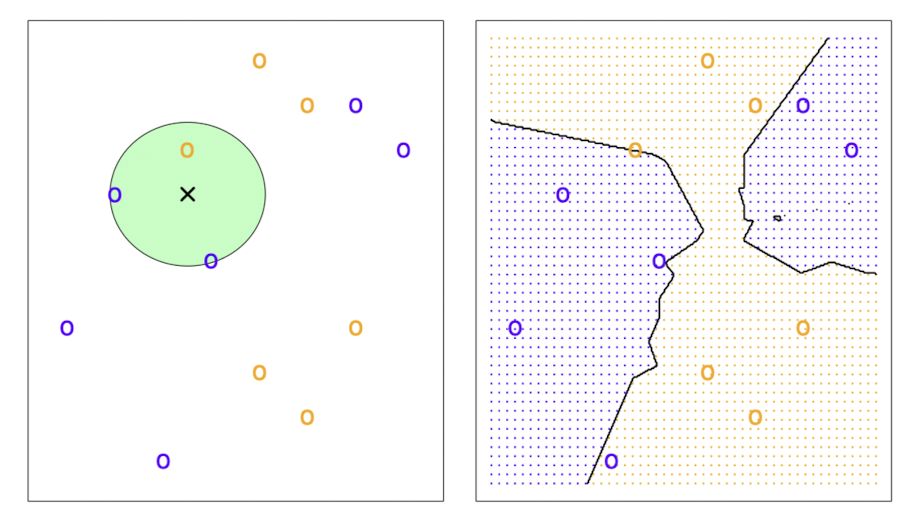
훈련 데이터 $x_0$에 가장 가까운 $K$개의 점을 식별하고, 그 점들의 집합을 $N_0$이라고 하자.
$N_0$ 내 각각의 클래스에 대한 조건부 확률을 그 비율로서 추정한 뒤 그 중 가장 높은 확률을 갖는 클래스로 $x$를 분류하는 것이다.

위의 왼쪽 그림은 K=3인 경우인데, 파란색의 비율이 2/3, 노란색이 1/3이므로 관측치 $x$는 파란색 클래스로 분류하게 된다. 오른쪽 그림은 모든 관측치에 대해 같은 방법을 적용하여 그린 KNN 결정 경계이다.
그럼 K값이 변함에 따라 경계가 어떻게 변화할지에 대해 알아보자.

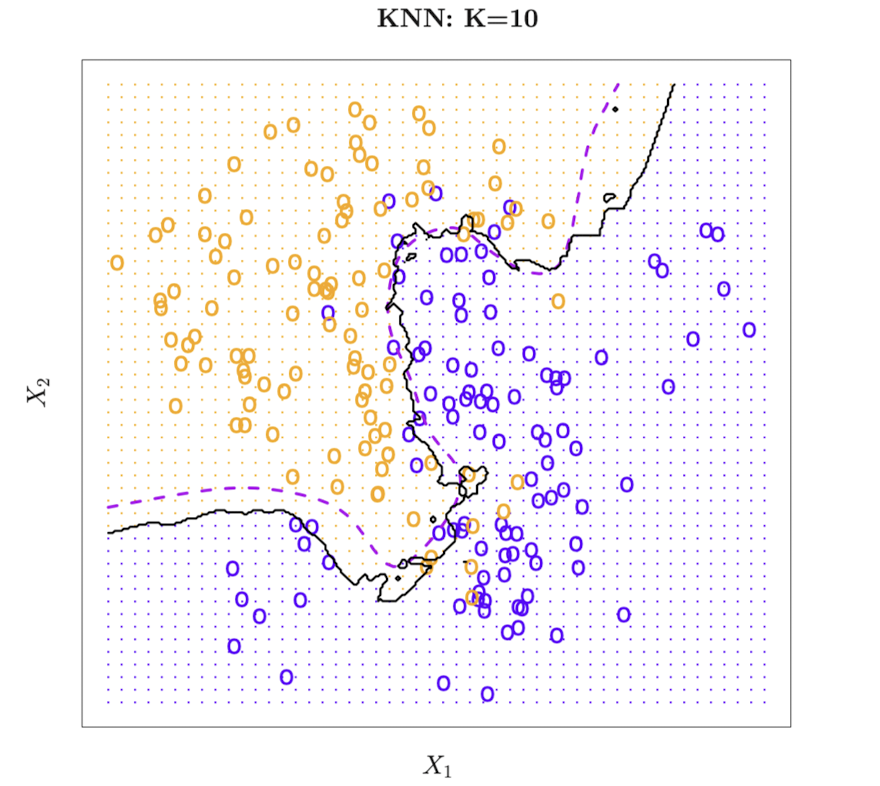
위 그림은 검은 실선으로 K=10 KNN 결정 경계, 보라색 점선으로 베이즈 결정 경계를 표시한 것이다.
두 경계가 상당히 유사하다는 것을 알 수 있다.

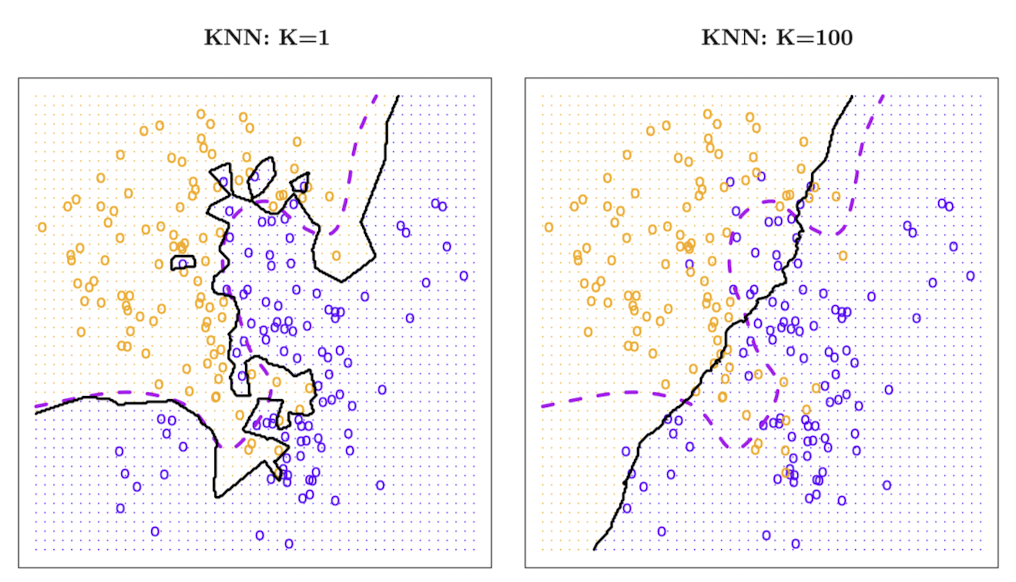
위 그림에서는 K=1과 K=100 KNN 결정 경계를 비교하고 있다. K=1일 때는 경계가 지나치게 유연하여 훈련 데이터에 과적합된 모습을 보이며, K=100일 때는 경계가 너무 단순해 데이터의 변동을 제대로 표현하지 못하고 있다.

따라서 KNN 모델에서는 모델의 유연성을 위해 적절한 K값을 선택하는 것이 중요하다.

위에서 다룬 이론을 바탕으로 class 라이브러리의 knn() 함수를 이용하여 주식 시장의 변동을 예측해보자.

> library(class)
> train.X = cbind(Lag1, Lag2)[train,]
> test.X = matrix(c(Lag1, Lag2), ncol = 2)[test,]

시뮬레이션의 결과를 재현하기 위해 랜덤 시드를 설정해준다. 우선 K=1 모델을 적합했다.

> set.seed(1)
> knn.pred = knn(train.X, test.X, Direction.train, k=1)
> mean(knn.pred == Direction.2005)
[1] 0.5

결과는 그렇게 좋지 않은데, 관측값들 중 50%만이 옳게 분류되었다. K=1 일 경우 훈련 데이터셋에 과적합 될 가능성이 있기 때문에, K=3으로 늘려서 다시 모델을 적합해보자.

> knn.pred = knn(train.X, test.X, Direction.train, k=3)
> mean(knn.pred == Direction.2005)
[1] 0.531746

K=3 으로 설정하니 약간의 성능 향상이 있었다.