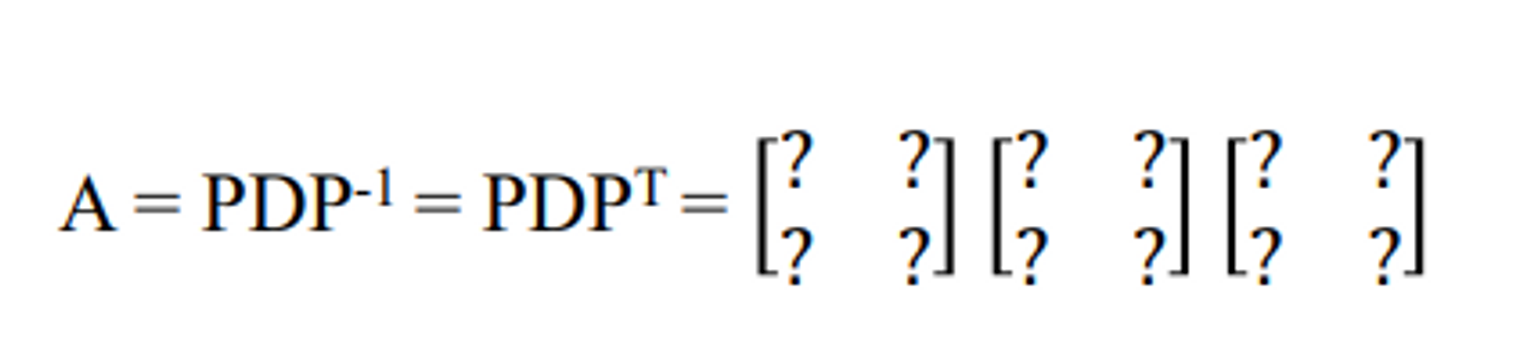💡 SVD 요약 : 매트릭스 연산(늘리고 돌리기)을 쉽게 보기 위해 나눔

• $A = UΣV^*$ : Σ mxn 일때 함
• $A^{-1} = VΣ^{-1}U^T$ : 인버스를 구하고 싶어서 Σ mxm 정방 행렬 + full rank라고 하고 품
  → 위 조건을 만족하지 않으면 어떻게 풀까? singular value가 0이면?
  

⇒ psuedo inverse : $A^†$

0이 곱해져서 되는 것만 살리고 안 되는 것을 알아서 잘 해보자 한 번

• $A^{†} = VΣ^{†}U^T$ : 수도 인버스 사용해 다음과 같이 변환 (Σ mxn)

• Jacobian psuedo inverse : $J^†$

• Dammped

🖤 Singular Value Decomposition 🖤

📌 SVD Introduction

pseudo-inverse matrix를 이해하기 위해서는 svd를 이해해야 한다

• eigen decomposition and polar decomposition 연관이 있다.
• In linear algebra, the SVD of a matrix is a factorization of that matrix into three matrices
  • factorization - 매트릭스를 조금 더 풀기 쉬운 것으로 쪼갠다
    -> 수학적으로 풀기 쉬운 상황을 많이 만들어주기 때문

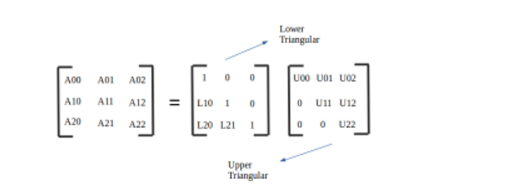
• Ax → 행렬 A를 곱한다는 것은
  → Linear Transformation : 일반적으로 벡터는 회전을 하는 것 or 늘어나는 것 즉 늘리거나 돌리거나 한다는 것이다.
  

✔ Transpose

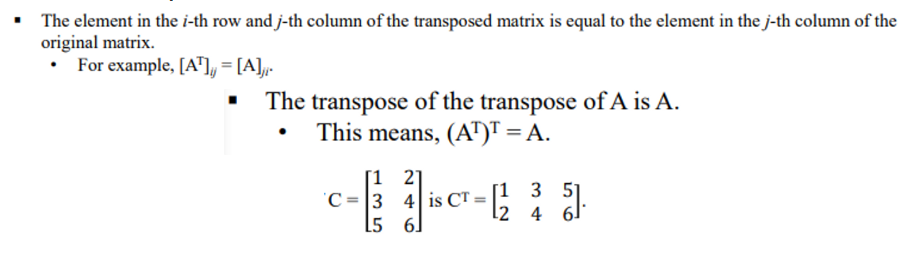
✔ Partitioned Matrix

매트릭스를 col 벡터들로 나누거나 row 벡터들로 나누는 것

📌 Eigenvalues & Eigenvectors

( 고유값과 고유벡터 )

$Au = λu$

• u : Eigenvector
• λ : Eigenvalues

• direction을 바꾸지 않고 벡터의 magnitude를 바꾸는 것은 scale을 곱하는 것밖에 없다
  • a vector u, and a scalar quantity λ, λu
  • Au = λu
    : u에다가 A를 곱해 회전하거나 스트래칭한 것과 똑같은 상황이 되는 λ를 eigenvalue of A 라고 한다
• 사실 중요한건 eigenvector이다.
  어떤 매트릭스에 eigenvector u를 곱하니 회전도 당하고 스케일리도 당했는데 사실은 그냥 스케일링 당한 거와 똑같게 된다는 것이다

📌 Eigen Decomposition of a matrix (AP = PD)

The matrix decomposition of a square matrix A into eigenvalues and eigenvectors is a kind of “matrix diagonalization.”

• A : eigenvalues들을 가짐

✔ Eigen Decomposition of a matrix

앞에서 Au = λu 를 설명함

→ 이것을 매트릭스 폼으로 AP = PD 로 만든다.

AP = PD를 만들면 P하고 D를 안다는 가정 하에 아래와 같은 꼴로 만들 수 있고 이로 인해 A의 역행렬도 다음과 같이 표현이 가능하다.

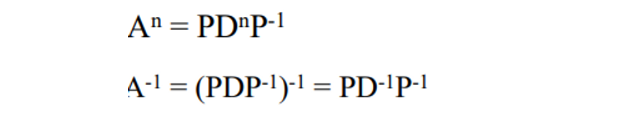
💭 예제

• P 가 orthogonal matrix 직교 행렬일때 아래와 같은 수식이 성립한다

orthogonal matrix : 직교 행렬

• $P^{-1} = P^T$
• Jacobian Transpose는 inverse를 구하지 않고도 풀 수 있는데 이게 바로 이 성질을 이용한 것
• 당연히 orthogonal이 아니기 때문에 잘 안되었던 것인데 그래서 그냥 너 거의 almost orthogonal이라는 가정을 하고 transpose를 한다
  

📌 Singular value

SVD를 설명하기 전에 일단 singular value A에 대해 이야기해보자

The singular values of a matrix are a set of numbers that can provide useful information about the matrix

→ Information? – matrix rank, pseudoinverse, etc.

$A^TA$

• m×n matrix A
• singular values
  • eigen value of $A^TA$ 에 suqre root를 한 값
  • denoted $σ_1, … , σ_i$ 로 표현, where i is the rank of A.

📌 Rank

• 선형대수에서 the rank of a matrix A is the dimension of the vector space generated by its columns
  → A의 랭크는 linearly independent columns of A 에 의해 결정됨
  
• 필수 불가결한 벡터의 개수
• full rank : m개가 전부 다 linearly independent , 이 매트릭스로 인해 표현되는 각 벡터들은 모두 자신만의 차원을 정의하는데 사용된다.

linearly dependent (선형 독립)

• set of vecter a, b, c가 있다.
  → c = 2a + b가 되면 c라는 벡터를 새롭게 정의할 필요 없이 a와 b로 나타낼 수 있다는 것이다.
  → [a b c] : Rank 2
  → Geomatric 관점 : c는 새로운 차원을 정의하지 않는다.
  

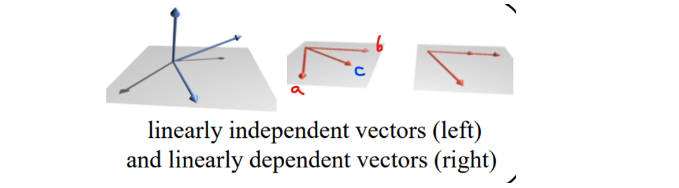
linearly independent

• 3차원 좌표계를 정의한 벡터들 x = [1 0 0 ] y = [0 1 0] z = [0 0 1]

💭 Example

• 세번째가 linearly independent
• c = a - b
• 보통 이렇게 간단하게 나오진 않는다

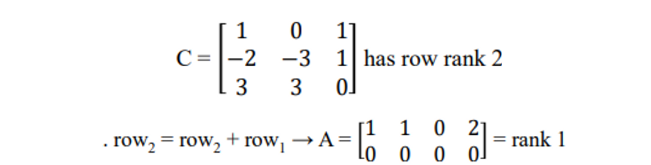
Then, how to solve?

-> 어떤 row가 0으로 변할 수 있는지 체크

row reduction

• 내가 현재 어떤 row가 있을 때 다른 것들을 어떻게 하면 되지?
  → 앞에 것들을 차례대로 0으로 만들면서 풀어 나간다.
  

📌 SVD

• The SVD of m×n matrix A is given by the formula $A = UΣV^*$
  • U: m×m complex unitary matrix.
    → col vec
    
  • Σ: m×n rectangular diagonal matrix with non-negative real numbers of the diagonal.
    → 대각선에만 정보가 들어 있는
    
  • V: n×n complex unitary matrix.
    → row vec
    → unitary matrix : $U^*U = I$를 만족하는 matrix
    

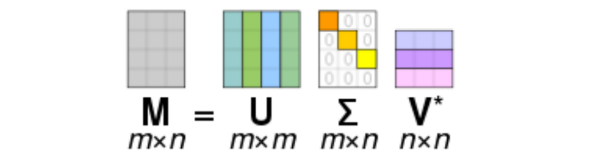
💁‍♀️ 실수부에서 다룰 때

• A가 실수 일 때, U와 V도 real orthogonal matrices, 이럴 때 SVD is often denoted $UΣV^T$
  → conjugate 는 허수부의 부호를 바꾸는데 실수라고 가정했으니 부호가 변하지 않는다. 즉 $V^* => V^T$ 실수부만 쓰기로 했기 때문에 conjugate는 사라지고 transpose만 남는다
  
• Σ : A의 singular values
  → singular values : $A^TA$의 eigenvale에 루트 씌운 값 (A를 분해할 때 사용)-
  
• The columns of U and the columns of V : left-singular vectors and right-singular vectors of A
  → sets of orthonormal bases
  

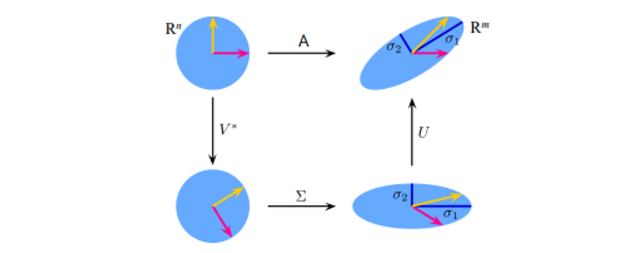
📌 Geometric meaning of SVD

• Eigenvector : it is stretched by the transformation
  벡터에 매트릭스를 곱한다는 것은 포인트 벡터를 돌리고 늘리고 하는 것과 연관이 있는 이야기라고 했다. 즉 어떤 방향으로 늘어날지 Scaling에 관련된 것
  

stretch하는 방향이 Eigenvector와 관련된 것, 얼마만큼 땡길거냐는 Eigenvalue에 관한 값

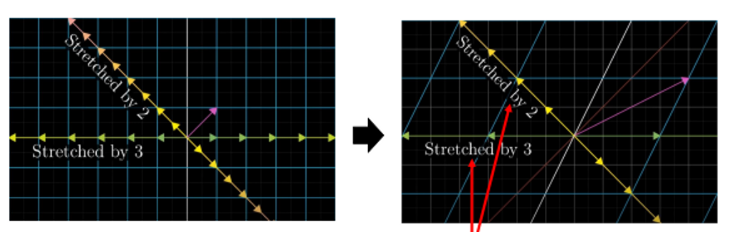
• 벡터를 돌리고 회전시켜 벡터가 아래처럼 변했는데 뭘했는지 알기가 너무 어렵다. 그래서 이해하기 쉽게 몇번의 회전 과 몇번의 늘림으로 표현한 것이 SVD이다

SVD를 사용하는 이유, 장점

• 매트릭스를 조작하는 과정에서 세분화해서 할 수 있다.
• 문제가 조금 더 쉬워진다. 단순한 로테이션과 스케일링으로 나타냈기 때문, 이를 나중에 다른 조작으로 풀어내기 쉬워지기 때문에 많이 사용한다.

📌 SVD calculation ($A = UΣV^T$ )

SVD를 실제로 계산하기 위해서는 $A^TA , AA^T$를 이용해야한다.

실제로 계산하기 위해서는 머리가 터지지만 pyhton에서 get svd 하면 빰하고 나오지만 계산과정을 알아야 뭔갈 할 수 있기 때문에 지금부터 배워보겠다.

• The eigenvectors of $A^TA$ make up the columns of V
• The eigenvectors of $AA^T$ make up the columns of U.
• The singular values in Σ are square roots of eigenvalues from $A^TA , AA^T$ → 두개의 eigenvalue결과가 같아서 어떤 걸로 해도 상관이 없다
  

SVD Example

💁‍♀️ 여기까지..

지금까지 psuedoinverse를 풀기 위한 기초였다. Eigenvalue, SVD 등을 배웠다.

이제부터는 Jacobian의 psedoinverse를 풀기 위한 방법을 배울 것이다.

---

🖤 The Moore-Penrose Pseudo Inverse 🖤

📌 Moore-Penrose inverse $A^+$

• inverse matrix를 구할 때 가장 많이 사용

• 보통 별도의 표시가 없으면 Moore-Penrose inverse 다.

• 그냥 수도 인버스라고 부르기도 함

• 보통 수도 인버스를 활용하는 가장 많이 사용하는 예시가 best fit
  -> 내가 주어진 데이터에 가장 근사한지 할 때

• entries가 real 이나 complex로 되어 있으면 보통은 unique한 해를 갖는다

📌 Pseudo-Inverse and Least Squares

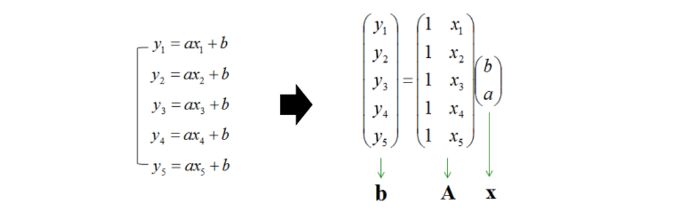
The method of least squares is a way of “solving” an overdetermined system of linear equations Ax = b, a system in which A is a rectangular m×n matrix with more equations than unknowns

overdetermined

• 너무 관측값이 많은 것
• y = ax + b 이면 식이 2개가 있으면 연립방정식을 풀 수 있다. 그런데 주어진 연립방정식이 너무 많은 경우가 이에 해당한다.
• 게다가 이 모든 것들이 노이즈가 껴 있어서 하나의 식으로 수렴하지 않아 문제가 된다.

• 계속해서 반복해 대입하면서 에러를 최소화한다.

• this point moves along a straight line y = dx + c

  작은 오브젝트의 모션을 관측했다고 가정해보자

  단위 시간 동안은 직선 운동을 한다고 가정하자
  

• 3개의 위치를 관측했다. 다음과 같은 equation을 만들 수 있다.

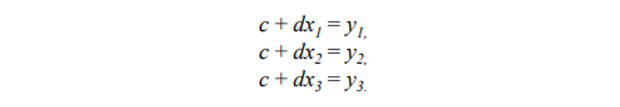
• 관찰에 노이즈가 껴 있기 때문에 직선 운동을 한다고 했지만 딱 직선 위에 관측이 안될 수 있다.

• 즉 에러가 존재해 SYSTME이 풀리지 않을 수 잇다.

• 에러가 있을 것 같으니까 e를 더해준다.

  그리고 e 빼고 다 이항 시킨다. 그리고 이것들을 모두 더하면 sum of the squares of the errors (SSE) 이 된다.

  ⇒ 즉 SSE를 0으로 만드는 방식으로 해를 구해야한다
  

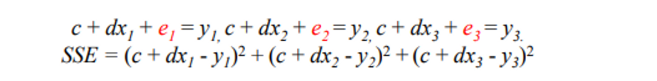
• We can rewrite the problem as y = Ax + e.
• Our goal is to minimize $e^Te$

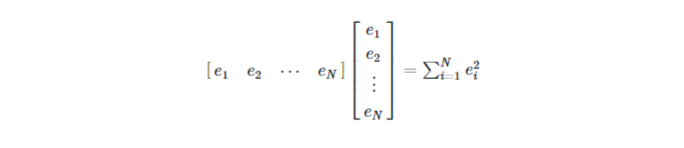
• 풀면 다음과 같다.

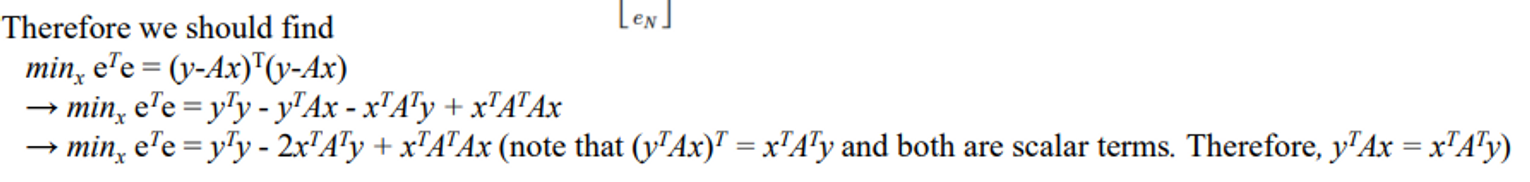
• 편미분에 대한 정의로 풀면 아래와 같이 된다.

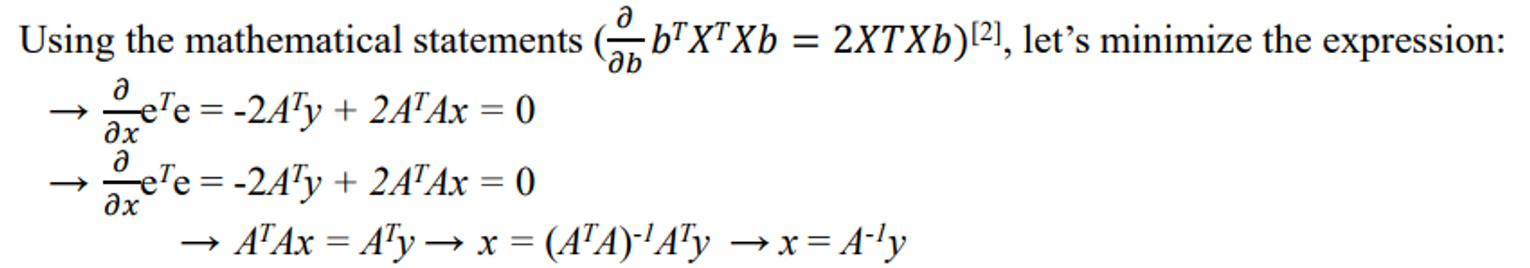
• 따라서 다음과 같이 말할 수 있다
  

---

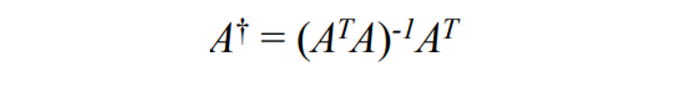
🖤 SVD and Pseudo Inverse 🖤

Moore-Penrose inverse 는 조건이 만족되어야만 쓸 수 있다. 근데 대부분의 상황에서 조건이 만족이 되고 만족이 안되더라고 하더라도 너는 만족이 된다 최면을 걸고 썼다. 근데 엄밀히 Moore-Penrose를 쓸 수 없는 상황이 있다. 그럴 때 SVD Pseudo Inverse를 사용한다.

📌 Pseudo Inverse and SVD

✔ computing inverse matrix using SVD

• 앞에서 배울 때는 Σ가 mxn matrix 였는데 여기서는 mxm이다
  → 왜냐면 앞에서 inverse matrix가 존재한다고 가정을 이미 했기 때문이다. inverse 가 존재하려면 mxm(정방행렬)이어야 하기 때문이다.
  

• $σ_i$ : singular values of the matrix A

• the columns of U : left singular vectors

• the columns of V : right singular vectors.

• U and V are orthogonal

  → their transposes are equal to their inverses $U^T = U^{-1}$, $(U^TU = I)$

  → Then, the inverse of A can be determined by $A^{-1} = VΣ^{-1}U^T$, where
  

→ 근데 이 식을 봤더니 A의 inverse를 한 것이 그냥 A랑 거의 비슷하므로 이제 $A^{-1}$을 사용하게 된다.

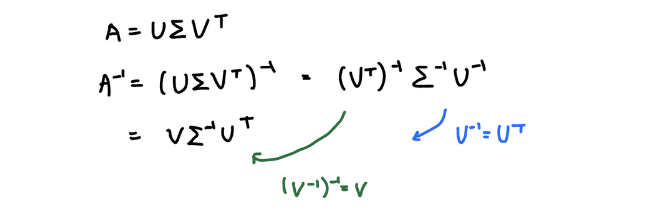
💁‍♀️ 문제점

• 앞에서는 쉽게 구했다. $Σ^{-1}$ 가 그냥 싱글러 밸류 역수이고 U랑 V도 다 알고 있으니 엄청 빠르게 구할 수 있었다.
  → 근데 우리가 이걸 mxm 매트릭스라고 가정하고 풀었다.
  싱글러 밸류가 m까지 다 들어가 있는 full rank이다. 두가지 조건이 들어간다. A 매트릭스가

  1. Full Rank matrix ( A가 zero singular value를 갖지 않음)

  2. mxm의 square matrix

     ⇒ 근데 이렇게 되면 nxm의 overdetermined 문제를 풀지 못한다.

그래서 psuedo inverse가 튀어 나온다.

In overdetermined systems matrix A does not have a unique inverse

• 만약에 full rank가 아니어서 시그마 값중에 0이 존재하면 $Σ^{-1}$은 존재할 수 없다.

  → 1/0 등장해서 인버스를 구할 수 없는 상황이 된다
  

• 더 자세하게 말하면, 싱글럴 밸류 0을 가지고 있으면 ..
  destory → geometry하게 설명을 해야한다.
  어떤 매트릭스 A를 곱했다는 것은 다른 차원으로 A가 날라갔다는 것을 의미, $A^{-1}$은 다시 돌아온다는 것을 뜻함.

  → 근데 싱글러 밸류에 0이 존재한다는 것은 차원을 넘어갈 때 싱글러 밸류 0이 간섭해서 곱해지는 데이터가 날아간다는 것이다. 원본데이터가 1 2 3 이든 0이 곱해져서 다 사라지는 것이다. 이로 인해 A의 역으로 가려니까 뭔지 모르겠는 것이다.

  ⇒ 즉 0을 곱함으로 인해 데이터가 소실된다는 것이다
  

0을 곱해 없애는 대신 어떻게든 살려보려는 노력을 해보자

• The matrix that recovers all recoverable information is called the pseudo-inverse and is often denoted A†

  → 완벽하게 복원 못하는 것을 맞으나 일단 복원가능한 애들은 복원해

  →싱글러 밸류를 곱해 차원 변환이 되었는데 반대로 가는 클루들이 충분해 복원할 수 있는 것들은 복원하고 잘 모르겠는 애들은 적당히으로 왠지 이거일 것 같으데 느낌으로 복원

  → 이것이 psuedo-inverse를 구하는 것이다.
  

• 0이 아닌 싱글러 밸류 쪽을 기존과 같이 만들어주고 나머지들은 그냥 0으로 둔 상태로 곱한다

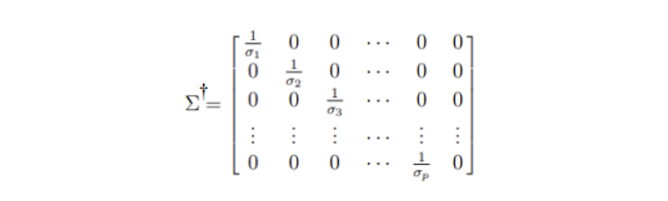
• 이전에는 $A^{-1} = VΣ^{-1}U^T$ 이었는데 $A^{†} = VΣ^{†}U^T$ 으로 바뀐다

📌 Jacobian Pseudo-inverse

• The pseudo-inverse of the Jacobian matrix is used when the matrix is not square or not invertible
  수도 인버스 자코비안은 매트릭스가 스퀘어가 아니거나 인버스가 아닐 때 사용하게 된다
  

✔ pseudo-inverse of J : $J^†$

• n x m matrix

• best possible solution to the equation $J∆θ = \vec{e}$ 을 제공한다

  → 세타가 주어졌을 때 end effecter의 desired 포지션 in change가 나오는 식이다. 원래는 $F∆θ = \vec{e}$ FK에서는 이건데 F라는 함수가 그냥 J라는 linearly approximation된 것으로치환해버리고 델타 세타 관측 개념으로 현재 내가 관측한 시점에서의 리니어 모션으로 approximation하는 것으로 정의했었다.

  → 그리고 이게 FK였기 때문에 반대로 풀어 IK를 구하려면 $J^{-1}\vec{e}^ = ∆θ$ 를 구해야한다. end effecte가 어떻게 움직이는지 position을 알고 있으면 나머지 관절들의 회전값이 구해지는 문제로 바꾸었다.

  → 여기서 $J^{-1}$이 필요했다. 근데 이게 없는 상황들이 종종 존재했다. 그래서 $J^{†}\vec{e}^ = ∆θ$ 를 풀어야 한다. 그렇기 때문에 $J^{†}$ J의 psuedo inverse를 구할 수 있으면 IK문제가풒ㄹ린다.
  

• 위에 두 개는 Moore 방식을 의미
  • m≥n : overdetermined
  • m<n : underdetermined (식이 부족함)
  • 두 조건이 다 안되면 SVD로 풀어야 한다

---

🖤 Damped Least Squares 🖤

📌 Introduction to Damped Least Squares (DLS)

💭 앞서 언급한 것들에 치명적인 문제

• 싱글러 밸류가 0 근처에 갔을 때 오작동을 잘 일으킨다

  수도 인버스를 사용하는 이유가 싱글러 밸류 문제를 잘 풀기 위해 사용하는 것도 있는데 싱글러 밸류 문제 근처에서 오작동을 일으키는 것을 잘 풀어보기 위해 제시되었다.
  

• 일반적인 인버스로 풀게되면 singularity problem을 절대 풀지 못한다

  → 혹시 풀 수 있다고 하더라고 singularity 근처에서 잘 안 풀린다.
  

• 이것을 해결하기 위해 수도 인버스가 등장한 것이다.

• 하지만 수도 인버스가 singularity 에서는 문제를 잘 풀지만 singularity 근처에서는 큰 오작동을 일으킨다.

• 이게 오작동을 일으키는 이유가

  중간에 $1 / σ$ 을 하는데 1/0이 되는거가 singularity problem이다.

  근데 이 σ가 0하고 가까워도 무한대로 가까워진다. 해가 구해지긴 하는데 갑자기 발산해버리면서 원하는 해가 안나온다.
  

• 그래서 Damped Least Squares가 나오게 된다.

✔Levenberg-Margquardt method

• $1 / σ+λ$ 를 한다. 이때 λ 는 tuning parameter이다

• 요 친구를 이용해 damping을 함

• λ가 충분히 커야 한다.

• 이런 것들을 정리하면 최종적으로 나오는 값은

이거다!

⇒ 분모에 $λ^2$을 더해주어 0으로 가는 것을 막음

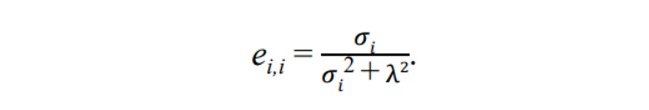
📌 Pseudo-inverse Damped Least Squares

• 형광펜 친 부분을 수학적으로 욱여넣었다

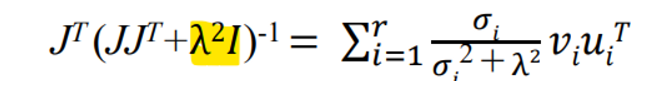
• 그래서 풀어봤더니 요러케 나왔다.

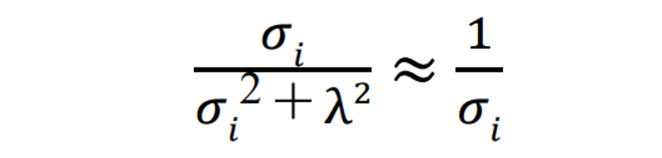
• 람다 근처까지는 값이 믿을 만하다는 이야기.

  ⇒ 람다를 설정함으로 인해 싱귤러리티 문제와 가까워지는데도 조금 더 stable하게 문제가 풀린다
  

• 그냥 least sqaure를 보면 싱굴러리티 근처에서 값이 막 발산함

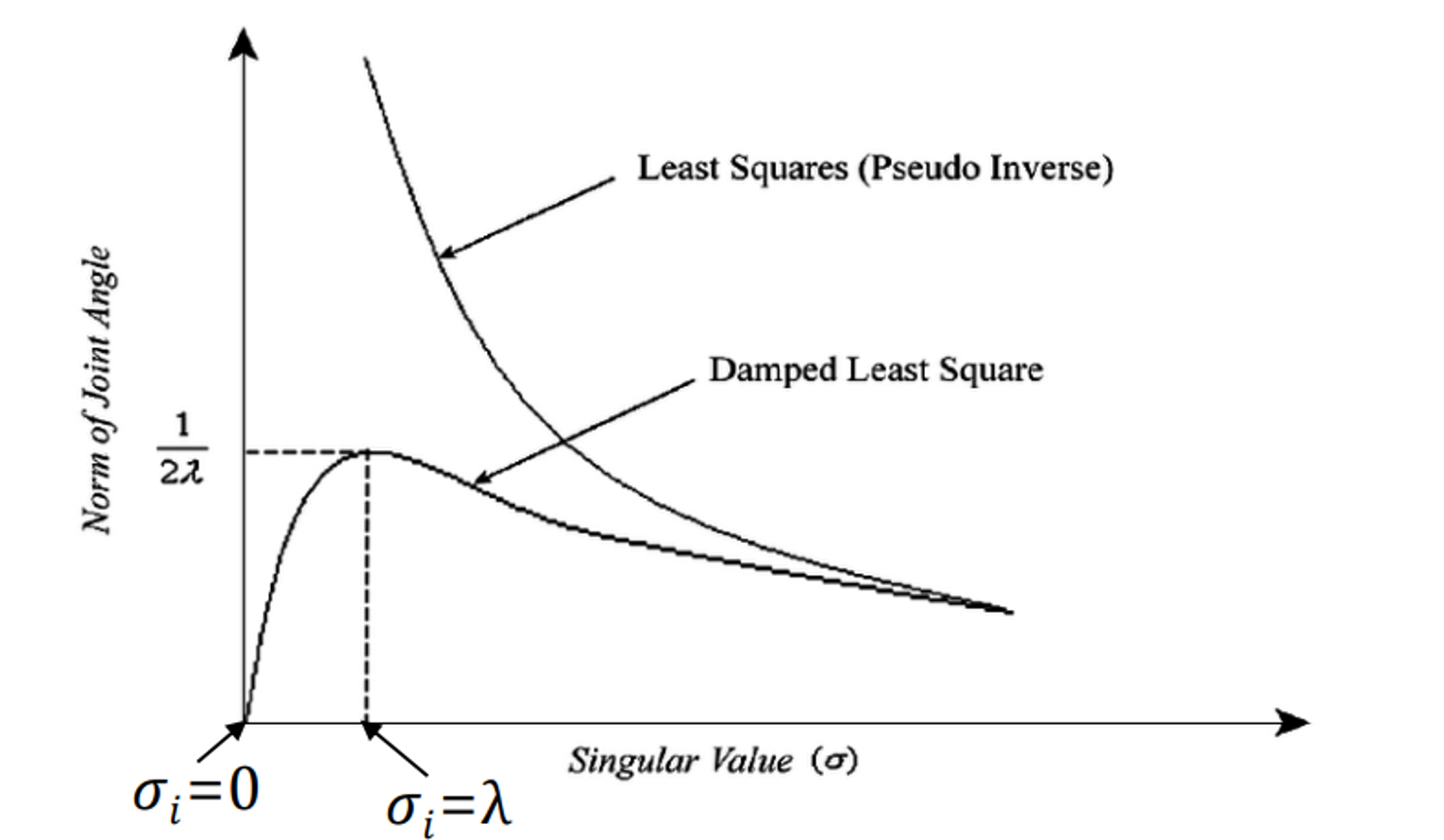
🧐 Damped Least Squares 정리

싱귤러리티 근처에서 발산하는 문제가 있어서 이 싱귤러리티 근처에서는 스테이블 하게 문제가 안 풀린다. 그래서 damping이라는 것을 분모에 넣어줌으로써 그 값 근처에서 까지는 stable하게 문제가 풀리도록 맞춰준 것이다.

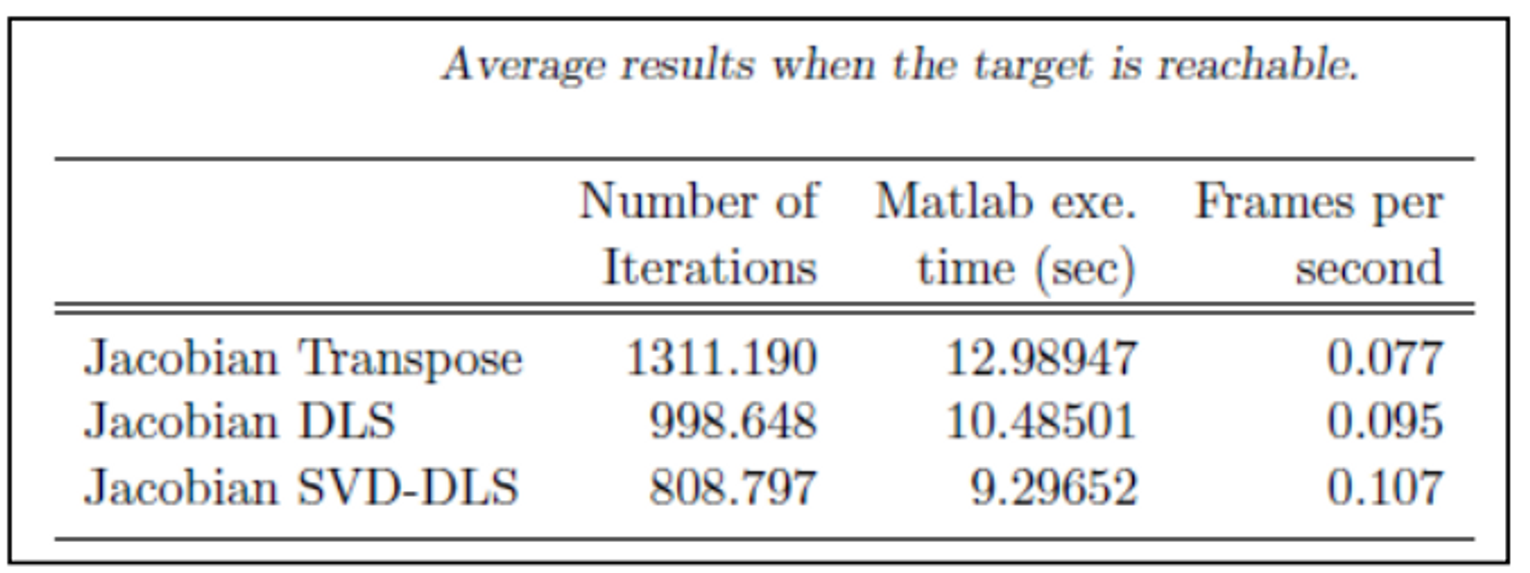
자코비안을 이용하는 것은 실전에서는 거의 안 쓴다. 다음 포즈 취하는데 0.1초 걸리는 것은 말도 안된다. 90년대 등장했을 때 로봇에 관점에서 많이 문제를 풀었다. 이 때 당시에는 느려도 상관이 없었고 문제 자체를 정의하는 것이 중요했다. 하지만 요즘은 빠르게 계산이 되어야 한다.

그러나 자코비언은 IK가 아니어도 다른 많은 곳에서 쓰이기 때문에 알아두면 좋다.

---

🖇 Reference

해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.