🖤 Introduction 🖤
📌 Newton Methods
Newton methods are iterative techniques used to solve nonlinear equations
자코비안은 문제를 수식 자체 하나만으로 "빰!"하고 풀어버렸다. 뉴턴의 방법은 해를 향해 점진적으로 전진해나가는 것이다. 단순히 문제를 가까이 간다는 것이 아니라 수학적으로 조금 엄밀하게 접근한다.
Problem definition
- 어떤 미지수를 풀 것인지 정의
- The IK problem is formulated as a system of nonlinear equations, where the unknowns are the joint angles or variables, and the goal is to find a solution that brings the end effector as close as possible to the target pose.
Problem linearization
- 선형적으로 풀어야 하는 미지수에 조금씩 다가간다
- linearization을 한다는 것은 이것을 직선으로 접근한다는 것이다. 충분히 작은 타임 스탬프에서 한다는 것이다.
Iterative update
- 그것을 iterative하게 반복한다
- linearization하는 것을 여러번 반복한다
Convergence check
- 충분히 했다고 생각되면 끊거나 에러가 너무 커지는 것 같으면 멈추는것
⇒ 이러한 방식들로 풀어내는 것들을 The Newton family of methods 라고 한다
- a second order Taylor series expansion을 이용해 풀게 된다.
- 어떤 f(x)가 있는 이것을 σ만큼 움직였다
→ 이것이 우변과 비슷하다
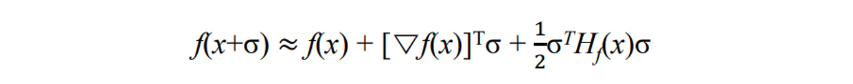
- Hessian matrix의 계산은 엄청나게 많은 비용이 든다. 심지어 뉴턴방식은 iteration을 돌아야 하니 엄청나게 많은 비용이 든다. 접근할 때 마다 Hessian을 구하고 해야한다.
→ 그래서 Hessian matrix을 구하는 대신 approximation of the Hessian matrix을 푸는 방식도 있다.- 대표적) the Broyden-Fletcher-Goldfarb Shanno (BFGS) method
📌 Newton Methods vs. Jacobian-based Method
Advantages of Newton method
Fast convergence
- initial guess(초깃값)이 충분히 좋다는 가정하에 convergence가 굉장히 빠르다.
- Jacobian보다 훨씬 빠르게 수렴에 도달한다
Quadratic convergence : iter을 반복할수록 빠른 수렴 + 적은 에러
-
특정 condition을 제공하면 Quadratic convergence을 제공한다
어떤 문제가 오든지 문제를 제대로 설정하고 condition을 지켰다면 시작만 하면 Quadratic convergence을 제공한다
Applicability to nonlinear problems
- 직관적인 해를 찾는다
- 자코비안은 해가 풀리지 않는 경우가 존재했다. 그래서 안 풀리는 경우에 traspose하고 damped 하고 별 짓을 다한다. damped 해도 싱글러 밸류 근처에서 완화만 될 뿐 이었다.
- 그러나 뉴턴의 방법은 그런 것 ㄱ없이 안정적으로 해를 찾는다
Disadvantages of Newton method
Sensitivity to initial conditions
- initial guess를 제대로 하지 못하면 헤맨다
Computation of Jacobian and Hessian
- 자코비안과 헤시안을 계산해야 한다는 코스트가 있다.
Inverse of Jacobian
- 이것까지 구해야 하는 경우가 있다…..
- 자코비안, 헤시안, 자코비안의 인버스까지? 장난행?
그래서 어떤 방식을 통해 최적화를 하게 된다. 자코비안은 한 번에 결과가 나오지만 뉴턴은 iterative 방식이기 때문에 approximation을 하게 된다.
🖤 Basics for Newton Methods 🖤
📌 Taylor Series
✔ power series의 한 종류
- f(x) : 모든 interval에서 given 가능하다.
- x = a일때 f(x)는 아래와 같이 정의 가능하다
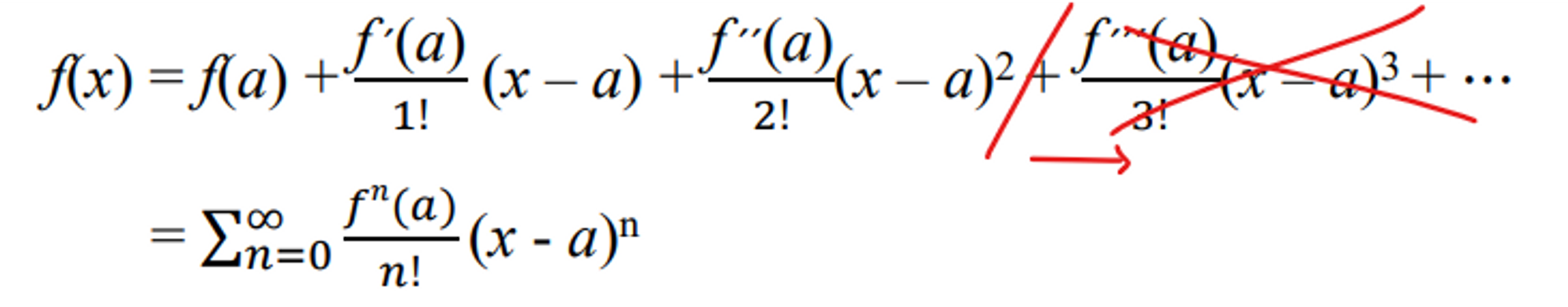
⇒ 모든 함수는 다른 함수들의 합으로 표현될 수 있는데 어떤 곡선은 그 곡선의 0차 미분 1차 미분 2 차미분 그것들을 어떤 방식을 통해 더해주면 표현이 가능하다.
⇒ 0차 1 차 2 차까지는 그래프의 모양에 영향을 주는데 3차부터는 작은 영향을 준다. 그래서 3차 부터는 무시해도 된다. 그래서 보통 2차 부분까지만 사용한다.
- If we set a = 0, then we have an expansion called the Maclaurin series expansion of f(x).
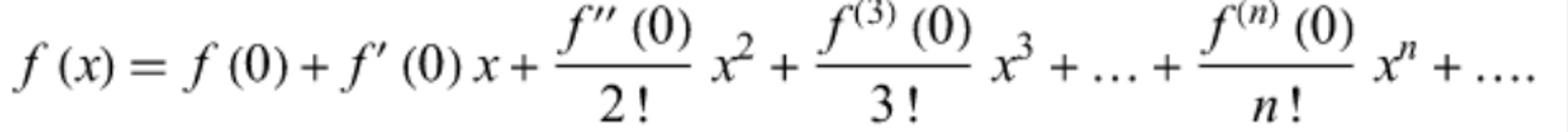
📌 Newton-Raphson Method (also known as Newton method) and IK
-
IK에서 Newton-Raphson method is referred Newton method
→ Newton-Raphson method : IK의 the roots of a nonlinear function을 찾는 것이다.
-
IK문제는 문제를 푸는 것이었다.
→ 이게 차가 0이라는 것은 goal position에 가 있는 것이다
→ F(x)가 0으로 가도록 minimize하는 문제를 풀고 있는 것이다.
✔ the solution to this problem is
→ Newton-Raphson root finding method을 적용할 수 있다
- initial guess → f 함수를 알고 있고 desired position도 알고 있으니 을 구할 수 있다.
- 빨간선 함수 인 곳에서 미분을 때려 slope가 나오는데 이것이 다시 x축과 만나는 점을 이라고 한다. → 이 과정을 계속 반복한다. 이것을 계속 반복하면 우리가 0으로 만들어야 하는 에 접근할 수 있다.
- slope는 y의 증가량/x의 증가량
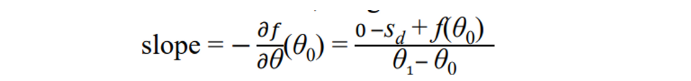
- 여기서 델타 세타를 구하면 아래 식과 같다
즉, 만 주어지면 △θ 을 바로 구할 수 있다.
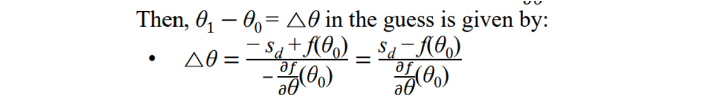
- update function
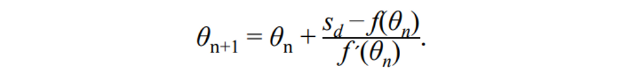
⇒ 이 과정을 반복할 수록 을 향해 간다 이를 통해 문제를 풀 수 있게 된다. 그래서 에 충분히 다가갔다고 판단했을 때까지 계산을 한다.
→ 근데 가 unknown이다. but 이다. 즉 이것을 이용해 보통 0.001 이하면 그만하게 된다. (threshhold이용)
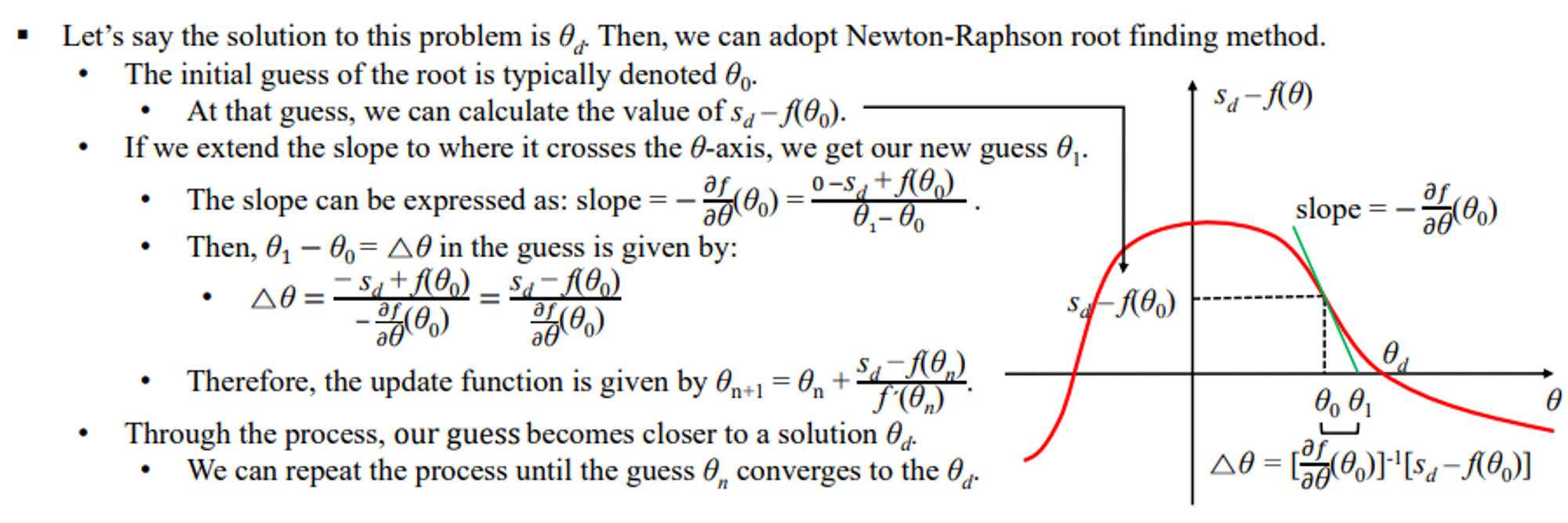
- y축은 : F(x)
- 빨간 선 함수는 우리가 모르는 함수
🖤 Newton-Raphson Method 🖤
root finding
- root finding은 0을 찾는 것이다.
Optimization
- Optimization 은 목적함수를 최소값으로 만들도록하는 것이다. 최소값은 반드시 0일 필요는 없다
⇒ 이 두개를 서로 상호전환이 될 수 있다.
📌 Newton Method and Optimization Problem
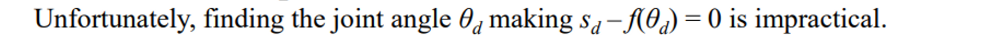
-
대신 이걸 뉴턴의 방법을 이용헤 최소화하는 방식을 optimazstion problem이라 하자
-
다음과 같이 정의
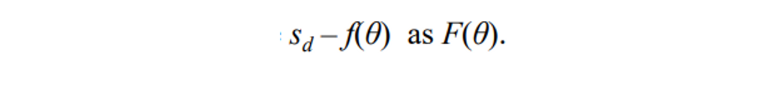
- 테일로 급수로 봐보자
- θ0 : initial guess
- △θ : 얼마나 움직일지
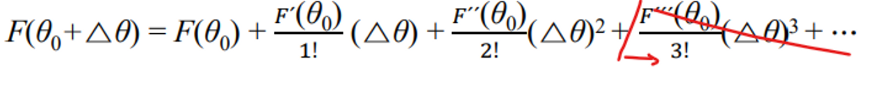
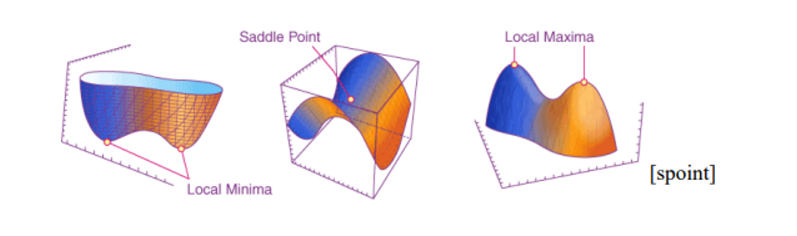
- (θ0+△θ) 가 최소(최대)에 이르길 원함 → stationary point에 도달했다는 것을 의미, 이것을 변곡점이라 한다. (일차 미분했을 때 0이 되는 점) → Stationary point can be of three types: local minimum, local maximum, or a saddle point
- 삼차 없애고 니분 한 번 했다. 그러면 아래와 같이 되고 정리를 하면 최종적으로 델타 세타는 블라블라 나온다.
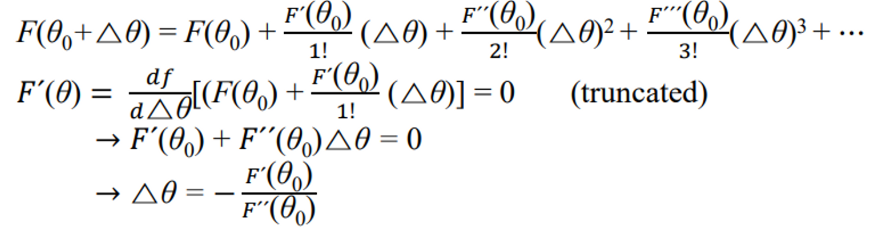
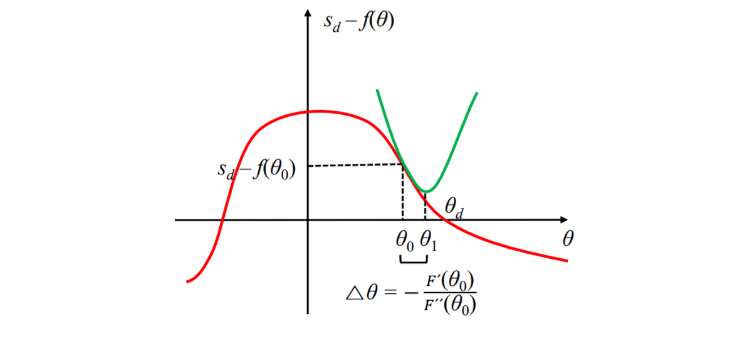
- 이거 그림으로 그리면 다음과 같다. 이전에 root finding을 할 때에는 선을 그어서 했는데 이제는 요러케 생긴 것을 그어서 이동한다.
📌 Multivariate Newton Method
-
IK problem is to solve the multivariate problem
Therefore, the single variable case (univariate case) should be
converted to the multivariate case.→ 앞에서는 미지수가 x 하나였는데 IK는 그렇지 않다.
→ 엔드 이펙터를 결정하는데 있어서 그에 관여하는 함수들이 여러개 이다. 그리고 이 세타들이 순수한 세타(다차원)들이 아니다. 즉 다차원 다방정식이다
-
뉴텀의 방식은 2개로 풀 수 있다는 것을 알았다.
-
0을 찾아가는 것 :
자코비안→ update funcion에 일차 미분만 들어감
-
미니넘 맥시멈을 찾아가는 optimization :
헤시안→ update funcion에 이차 미분이 들어감
-
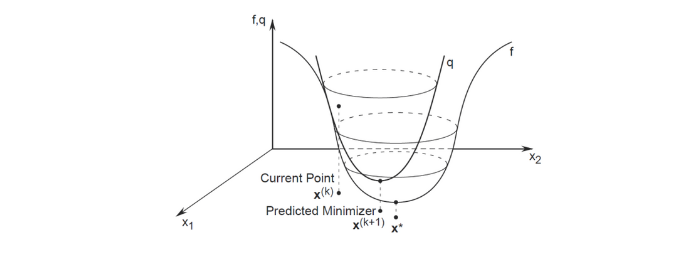
Let’s consider a multivariate root finding problem.
- The goal is to find the joint angles that satisfy the given end-effector pose end effecter의 pose가 주어졌을 때 가장 좋은 조인트 앵글을 찾는 것이다.
- the problem is formulated as a vector-valued function F(θ):
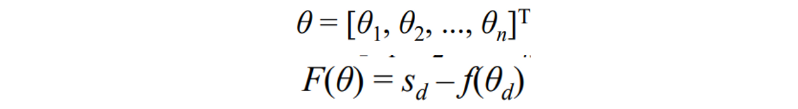
→ 가야하는 포즈 - 현재의 포즈 , 그리고 f는 그냥 FK 방식으로 품
- 다음과 같이 쓸 수 있다.
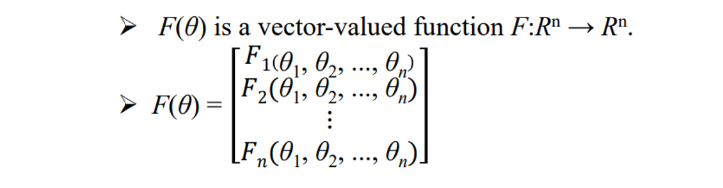
- 여러개의 Function과 여러개의 theta가 관여를 한다. 이것을 모두 일차미분을 시키기 위해 자코비안을 쓴다
- 이차미분은 무시한다. root finding에서

- 다음과 같이 정리가 된다.
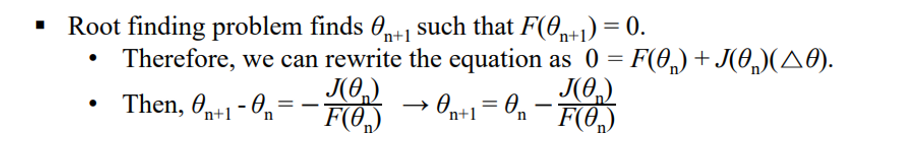
✔ 정리
1차 미분으로 풀었던 것이 J로 바뀌었다. J로 바뀐 것을 정리했더니 위와 같은 식이 나왔다.
✔ Multivariate Newton Method Example (root finding)
Assume that we have a robotic system with 4 end effectors and 8 joints, each defined by a three-dimensional
- Then F(θ) would be a 12-dimensional vector (3 position dimensions for each of the 4 end effectors).
multivariate optimization problem
-
The goal is to find the joint angles that minimize a scalar-valued objective function
-
우리가 앞에서는 0을 향해 가는 것 자체가 문제를 푸는 방식이었다. 근데 여기서는 이 e들의 제곱의 루트를 최소로 가는 것을 풀고자 함
→ root finding에서는 각자를 0으로 가는 것을 찾는 것이었음. 여기서는 최소화되는 것을 찾고자 하는 것이기에 그냥 다 더해버린다.

- The update function for the multivariate Newton-Raphson method can be derived using Taylor series expansion:

- 정리하면
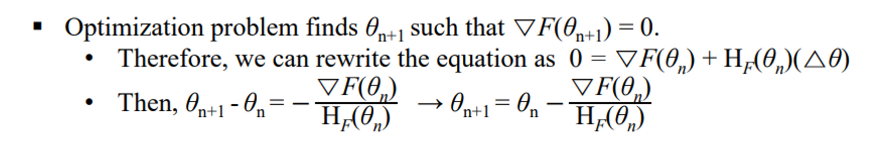
✔ Multivariate Newton Method Example (optimization)
왜 8x8이 나왔는지 염두해보고 공부

reciprocal of the second derivative
-
2차 미분 분의 일
-
함수를 얼마나 세게 업데이트 할 것인가? 델타 티를 구할 때 쓴다
-
얼마만큼 스템을 많이 갈 것인가를 결정할 때 사용
-
second derivative이 크면 거의 0으로 수렴
-
second derivative이 0과 비슷하면 reciprocal이 커진다. 즉 함수가 거기서 편평해진다는것이다.
아래 식을 보면 알 수있듯이 분모에 헤시안이 등장한다. 이 밑에 식을 쉽게 풀 수 있는 방법들을 이제 연구하기 시작한다.
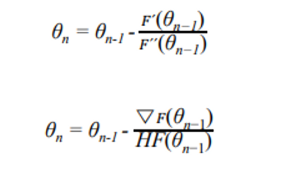
🖇 Reference
해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.