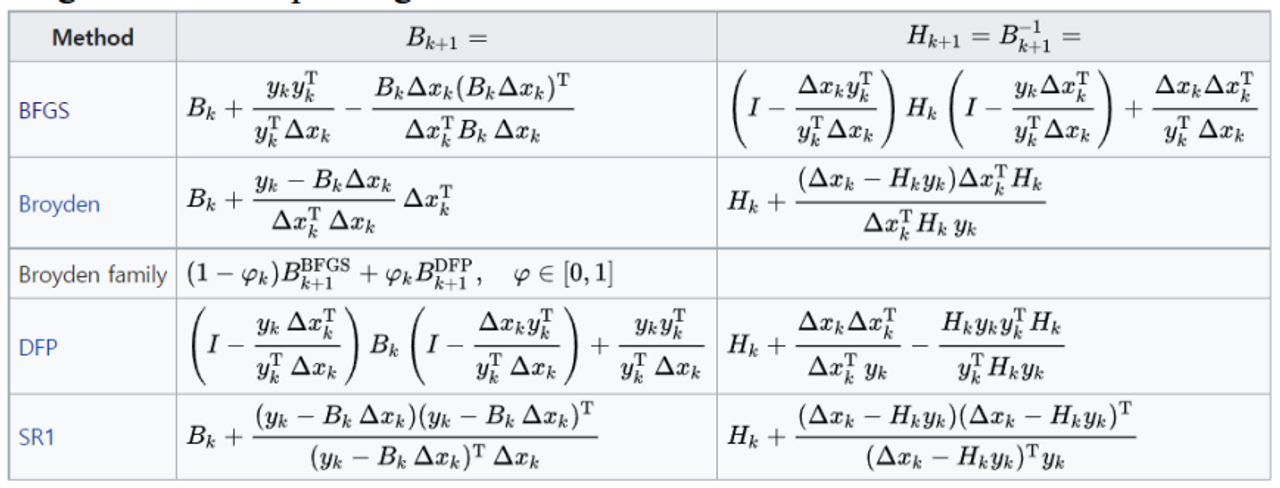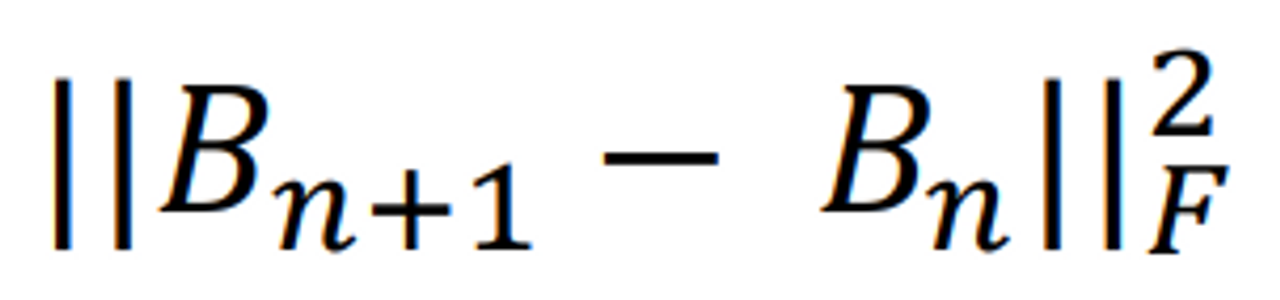5. Quasi-Newton Method for IK

🖤Introduction🖤
📌Quasi-Newton Methods
- 보통 이차 미분을 이용하는 method가 수렴이 더 빠르다.
→ it can be very expensive to calculate and store the inverse of the Hessian matrix at each iteration
→ 이차미분(헤시안)을 하는 것 자체가 굉장히 computational cost가 크다.
- 그래서 quasi-newton methods to approximate the Hessian 를 사용하게 된다.
→ 헤시안을 정확히 구하는 대신 approximate한다.
Quasi-Newton Computation flow:
- Start with an initial guess for the optimal solution.
- Compute the gradient at the current point.
- Approximate the Hessian matrix or its inverse.
- Update the solution using the approximated Hessian matrix.
- Repeat steps until a stopping criterion is met (reaching a maximum number of iterations or a desired level of convergence.)
📌Quasi-Newton VS. Newton method.
Advantages
- Reduced computational complexity.
- Faster Convergence (especially for ill-conditioned problems).
빠르게 수렴한다 - More robust as Quasi-Newton methods are less sensitive to the initial guess and can handle non-quadratic objective functions. 초기값의 상태에 조금 덜 민감하다. objective functions이 quadratic 하게 풀리지 않는다고 하더라도 괜찮다
Disadvantages
- Less accurate Hessian matrix.
뉴턴 메서드 비해 정확도가 떨어진다
- Slower convergence for some problems (when the approximations are not sufficiently accurate or when the problem is well-conditioned, the Newton method can converge more quickly than Quasi-Newton methods).
→ 초기값 자체가 이미 뉴텀 메서드로 충분히 수렴한 가능한 상태로 well conditioned되어 있는 상태에서는 굳이 쓸 필요가 없다. approximation이 들어가기 때문에 이게 잘 되지 않으면 충분한 성능을 내지 못한다. 실제로 아크로바틱한 동작에서는 잘 안되기도 한다.
🌊 Recent research topics:
- Improves hessian approximations.
- Parallelization and distributed computing.
- Application to machine learning.
- Understanding the convergence properties and establishing better stopping criteria.
🖤Basics🖤
📌Ill-conditioned problem
- 헤시안 매트릭스의 condition number 가 너무 크면 numerically challenging하게 만든다
-
condition number : ratio of its largest and smallest eigenvalues
eigenvalues 의 비율차이가 너무 클 때→ 벡터에 매트릭스를 곱하는 것이 Transform(회전 + 늘리는 것)을 의미했었다. 이때 가하는 힘을 e1, e2이렇게 나누어 표현했는데 만약 e1이 엄청 크고 e2가 엄청 작다면, e1가 가까운 쪽으로 움직이면 변화율이 엄청 크고 반대는 엄청 작다.
→ 분명 같은 timestamp로 움직이는데 한쪽 축으로는 팍 움직이게 된다.
→
delta x를 얼마나 설정하게 되느냐에 따라 수렴을 할 수 있을지 없을지 결정되는데 그래프의 변화율이 너무 커진다.
-
🌊 This can arise from various sources:
- Poor scaling of variables
- f(x,y) → x y가 scaling이 잘 못 됨.
- ex) 데이터를 인풋으로 넣어서 학습을 시키는데 어떤 것은 0-1000사이에 분포 0-100000000사이에 분포하는데 같은 파라미터로 두고 찾으면 안 찾아진다.
- High-dimensional problems.
- 너무 많은 파라미터를 쓰면 파라미터들 사이에 eigenvalue가 다양화되니
- Intrinsic properties of the objective function.
- 오브젝트 함수가 이미 그럴 수 밖에 없는 상황들이 있다.
🌊 This can be mitigated by using:
- scaling을 잘 한다
- Preconditioning
- ill-condition에 robost한 alrorithm을 사용한다
📌 Definite Matrix
한 마디로 그냥 명칭이다.

Positive-definite and positive-semidefinite은 convex optimization이라는 것에 기본이 된다
→ 포인트 p에서 헤시안 매트릭스가 양수이면 이 함수는 p에서 convex하다
→ p로 수렴한다는 것을 보장할 수 있다. itertative를 돌면 더 나은 해를 찾을 수 있는 것이 보장된다.
🌊 Definite matrix의 용도
- Definite matrices are important in optimization problems
→ curvature of the objective function를 제공하기 때문
→ 이 문제가 풀 수 있는지 없는지 판단할 때 이것이 positive인지 negative인지 판단하면 얼추 맞는다. 즉 많은 계산을 사전에 하지 않고도 문제가 풀리지 풀리지 않을 지 판단이 가능해진다.
-
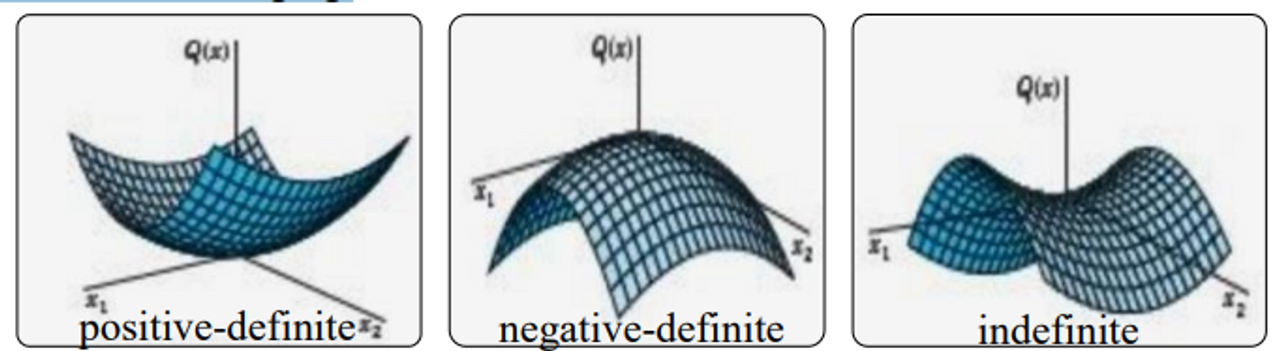
The properties of
positive-definite matrix Minclude1) all eigenvalues are positive
2) the matrix is invertible (역행렬가능)
3) the matrix is symmetric-
positive definite matrice는 convex functions에 매칭이 되고
-
하나의 global minimum 값을 갖는다
⇒ optimization 문제가 하나의 해를 갖는 것을 보장한다
-
-
The properties of
negative-definite matrix Minclude1) all eigenvalues are negative
2) the matrix is invertible
3) the matrix is symmetric.- 반대로 위쪽에 도달
-
그림에서
indefinite(3번째) 경우반드시 글로벌 미니멈이나 맥시멈으로 도달한다는 보장이 없다.
⇒ 문제를 optimization problem으로 풀 수 있을지도 없을지도 모를 때 definite matrix 성질을 이용해 미리 판단할 수 있다.
📌 Secant Method
-
root finding 알고리즘이다.
→ 뉴턴 메소드랑 비슷한 느낌을 가진다.
-
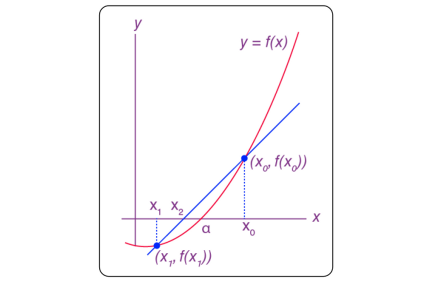
two previous points 를 이용해서 현재 추정중인 것의 일차 미분을 추정한다,
-
secant : 커브에서 두개의 distinct 포인트를 연결한 하나의 선을 말한다.
→ 원에서 지름을 지나지 않는 선
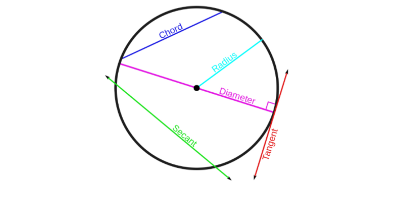
🌊일차 미분을 구할 수 없을 때 사용한다.
→ 함수 자체가 불가하거나 computational cost 때문에
→ 점 두개 이용해서 x증가량 y증가량 이용해서 마치 미분처럼 구할 수 있다.
→ 이차로 넘어가면 이전 두개 점에서의 일차미분과 값들을 이용해 구할 수 있다.
continuous function f(x)
- the goal is to find a root of the function
- 두개의 initial guess가 있다.
- iterative하게 돌면서 값을 찾아나간다

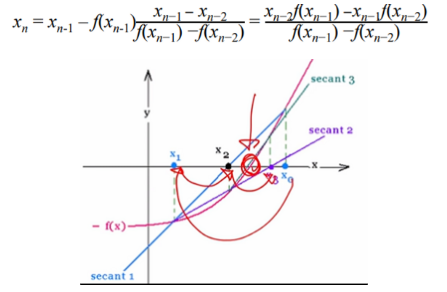
- recurrence relation
📌 Frobenius norm
- The Frobenius norm, also known as the Euclidean norm, is a matrix norm that is used to measure the size of a matrix
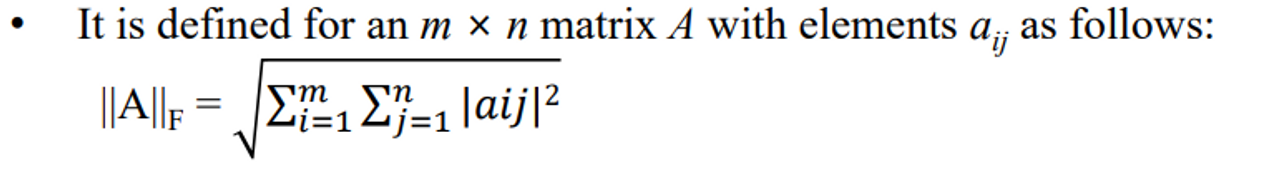
- The Frobenius norm has a relationship with trace properties
- tr(A) : 매트릭스의 대각성분을 전부 더한 것
- 아래 식과같은 성질을 가지고 있다.
real number로 오게 되면 conjugate가 사라지면서 가 된다.
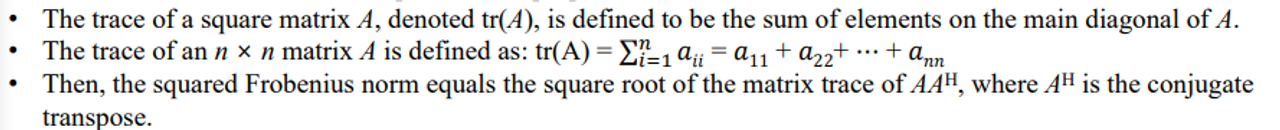
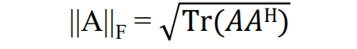
📌 Lagrange Multiplier
- Lagrange multiplier 은 optimization problem에 사용되는데 어떤 constraint가 function에 가해지는 상황에서의 최소와 최댓값을 찾는 것이다.
→ 이전에 어떤 함수를 그냥 optimization할 때는 함수만 미분을 했었는데 거기에 어떤 constraint가 걸렸을 때 최적화 문제를 푸는 것이다.
-
Lagrange multipliers 가 오브젝티브 함수에 적용
-
맥시멈 포인트를 찾고 있다면 등고선이어서 가운데로 갈 수록 값이 커진다.
→ g(x,y)로 constraint를 건다. 이 빨간선 위로는 넘어오면 안된다고 정하는 것이다.
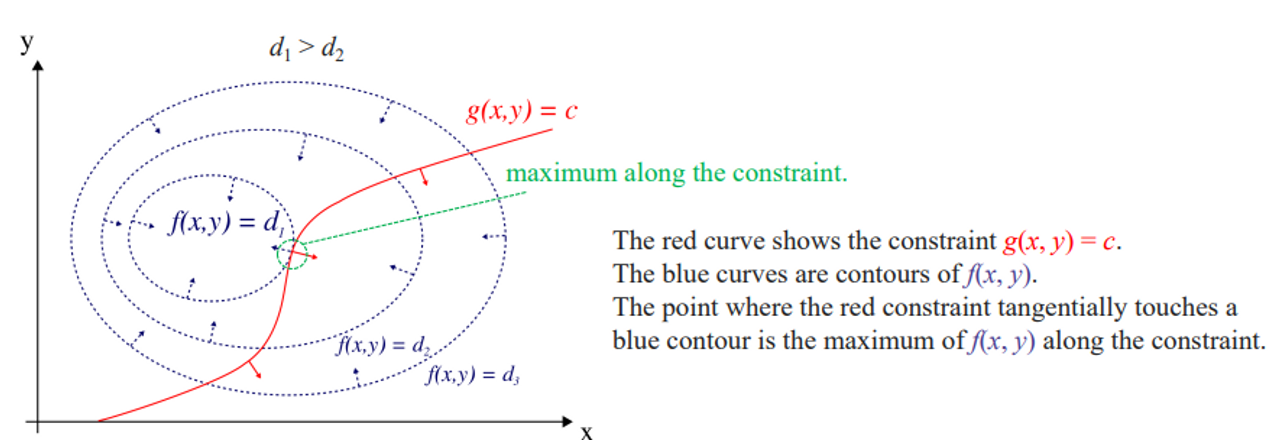
🌊 method overview
- f의 최대나 최소를 구하는 것이 목표이다.

- 아래와 같이 쓸 수 있다.
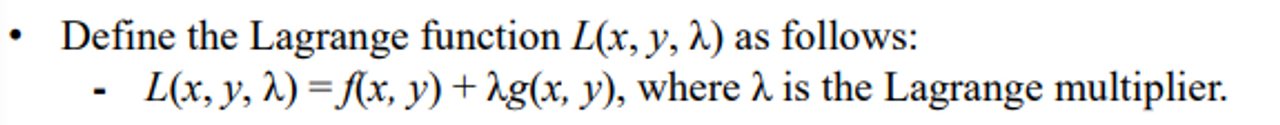
- 각각에 대해(3개) 모두 편미분을 한다. 그리고 이것을 모두 0으로 만드는 critical point를 찾는다.
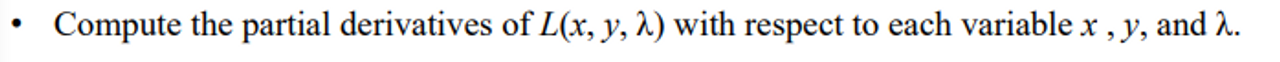
- 그리고 식을 풀어 optimal values for x and λ, y를 찾는다
- 구한 값들을 다시 함수f에 넣어 맥시멈 혹은 미니멈 값을 찾는다
⇒ multivariate 문제는 다루지 않는다. 너무 어렵기 때문^^
🖤Quasi-Newton Method🖤
ill-conditioned problem도 배우고 수렴하는지 수렴하지 않는지 사용하기 위해 Difinite Matirx도 배우고 secant method 이전 두 점의 일차 미분을 이용해 이차미분을 구할 수 있다는 것을 위에서 다루었다. Quasi-Newton을 수학적으로 정리하기 위해 필요한 Frobenius norm , Lagrange Multiplier 도 배웠다. 이 내용을 바탕으로 Quasi-Newton Method를 설명하고자 한다.
📌Search for extrema (optimization problem)
-
어떤 함수의
gradient = 0이되는 점을 즉일차 미분이 0이 되는 점을 찾는 것이다.- (Recall that ).
-
optimum region 근처에서는 Quadratic적으로 approximartion이 가능하기 때문에 수렴이 가능하다. 그렇기에 그 점 근처에서 gradient와 Hessian을 사용해서 그 쪽으로 향하도록 한다.
→ 여기 분모에 들어가는 헤시안을 approximation 할 것이다.
→ 다시 구하는 것이 아닌 이전에 구한 을 사용해 헤시안을 업데이트 한다. 이를 통해 코스트를 줄일 것이다.

How to approximate the Hessian matrix?
-
positive-definite matrix B를 이용한다.
-
이를 오브젝티브 함수의 그라디언트 정보를 이용해 업데이트 한다.
-
secant equation plays a crucial role in computing Hessian approximation based on the gradient information
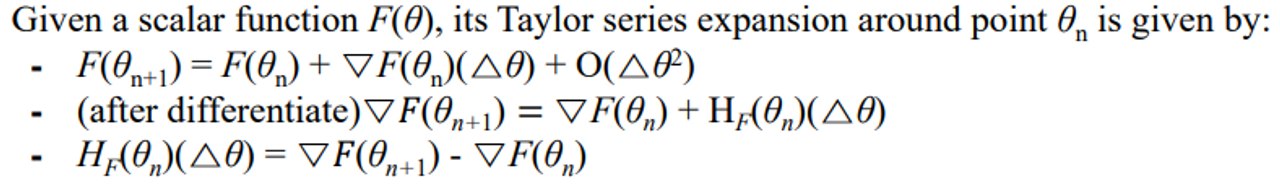
- 헤시안 매트릭스가 사이에서 거의 constant하다고 가정하면 바로 식을 넣을 수 있다. “헤시안 거의 비슷하지 않을까?” 하고 그냥 넣어버리는 데 정확하지 않은 헤시안을 뜻하기 위해
B로 표기
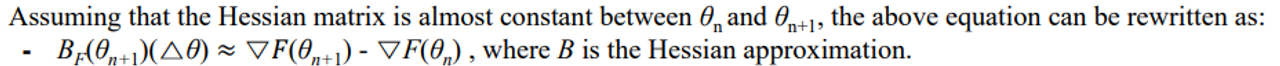
- 아래것들을 만족하게 된다.

- 아래 문제를 풀게 된다.

⇒ 여기까지는 Hessian Matrix를 일차미분 gradient로 부터 계산해내는 방법을 이야기 했다.
- 이전 스텝의 Hessian을 사용해서 현재 Hessian을 업데이트 하는 방법론
- There are several algorithms for updating B
Broyden-Fletcher-Goldfarb-Shanno Method
- BFGS은 최종보스이다.
- Positive definiteness : 결국 수렴할 수 밖에 없다
ex) SR1은 이것이 보장이 되지 않아 어떤 함수에서는 발산한다.
- Convergence 가 빠르다
- Numerical stability
→ SR1은 ill-conditioned Hessian approximations, which can cause
numerical difficulties.
- Positive definiteness : 결국 수렴할 수 밖에 없다
하지만 학부생 수준에서 다루기에는 어렵기 때문에 BFGS의 기본이 되는 Broyden Method Derivation를 다루도록 한다.
🖤Broyden Method Derivation🖤
- 목표는 다음과 같다
→ 수식을 통해 거의 같게 만드는 문제를 풀면 업데이트 함수로 진화할 수 있다는 것이다.
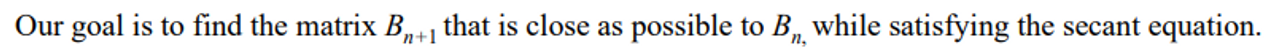
- This can be achieved by minimizing the Frobenius norm of the difference between Bn+1 and Bn, subject to the secant equation constraint:
-
지금 하고자 하는 것은 업데이트 전과 후가 비슷하도록 만드는 것이다.
-
secant성질을 만족해야한다 그래서 (subject to ~) 문장을 조건으로 건다.⇒ 무언가 minimize 하는데 constraint가 걸려있다 =>
Lagrange등장!
-
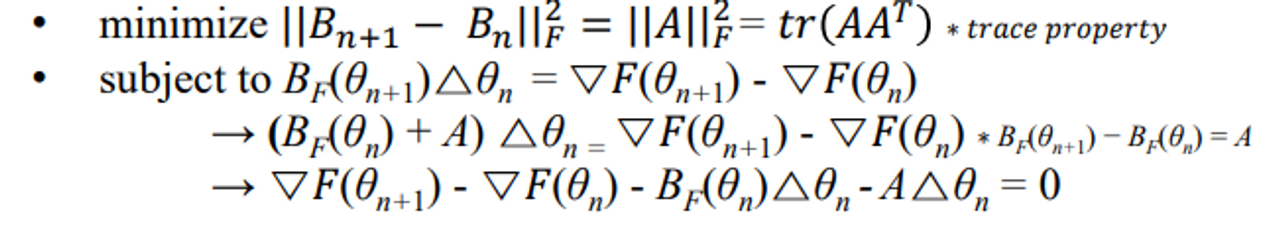
-
Here, Lagrange multiplier λ is used to form the Lagrangian:
- 그래디언트를 때리는데 람다는 사용하지 않는다. 왜냐면 어처피 0 이기 때문이다.
- A에 대해 편미분을 때리면 아래와 같은 식이 나오는데…
- 정리하면 최종적으로 식이 나온다.

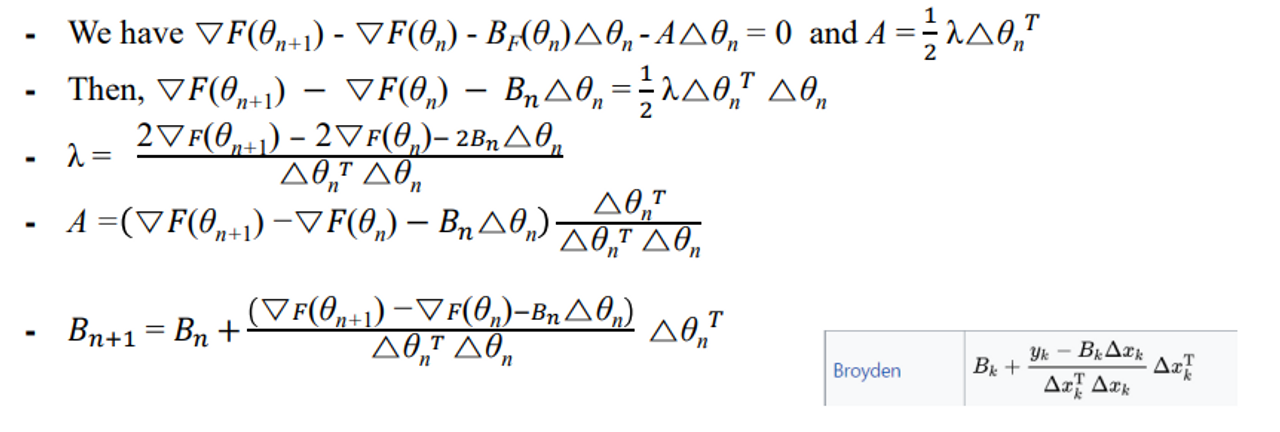
🌊 핵심 2가지 아이디어
- Hessian 을 업데이트 할 때 이 둘은 거의 차이가 없다.
- 그 때 이 것은 secant 성질을 만족한다
🖇 Reference
해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.