⚡ REVIEW ⚡

FK

루트로 시작하는 joint의 각도를 정의하면 child node의 joint의 위치를 결정할 수 있었다.

→ 각 joint의 세타값(각도)을 모두 알고 있으면 end effecter의 최종 포지션을 결정할 수 있었다.

⇒ 각 관절의 세타 값이 주어졌을 때 end effecter의 포지션을 정할 수 있다. 세타의 값을 모두 알아야 하기 때문에 힘들었다. 그래서 나온 것이 IK이다.

IK

엔드 이팩터의 x,y,z 포지션을 정해주면 나머지 joint의 각도를 다 정해진다.

🤍 Jacobian

• IK를 구하기 위해 inverse를 구해야한다
  → 이것을 linearly approximate하게 구하는 것이 $J^{-1}$ Jacobian의 inverse

  • 싱귤러리티 근처에서 잘 됐다.

  • invertable inverse가 존재해야했다

    → 그래서 Jacobian의 psudoinverse $J^+$ 등장하게 된다. 적어도 invertable 하지 않은 상황에서는 풀 수 있지만 여전히 Sigularity 에서는 문제를 풀지 못한다.

  • damped list 적용해서 조금이라도 더 신뢰하는 영역을 늘림

⇒ 여기까지 자코비안으로 푸는 것이었다.

🤍 Newton's method

• Newton method의 등장 (iterative + Quadatic conversion을 제공)
  iteration을 돌 때 굉장히 빠르게 해를 향해 나아감.

  • root finding : 0을 찾는 것

  • optimization : 변곡점을 찾는 것

    → 자코비안 보다 좋은 것은 빠르게 해를 찾을 수 있으며 상대적으로 Sigularity problem에 대해 자유롭다.

    → 반면 수렴을 하는데 Hessian Matrix를 사용하기 때문에 너무 많은 오버헤드이다.

    ⇒ Quasi-Newton Method 가 등장하며 이 단점을 없애버림

• 수학적으로 괜찮게 IK를 푸는 방법으로는 쿼시 뉴턴이다.

  → Quasi-Newton의 핵심 아이디어
  Hessian을 계산할 때 이전 스텝에서 구했던 Hessian과 현재 스텝에서 구한 일차 미분을 이용해 approximation하는 것이다.

---

여기서부터는 Heuristic Inverse Kinematics Algorithms 에 대해 살펴본다.

🖤 Cyclic Coordinate Descent

Iterative Heuristic Search

Cyclic Coordinate Descent (CCD)

우리 몸과 같은 관절체를 가장 빨리 구할 수 있는 방법

• 한번에 한 개의 joint를 옮겨 와서 포지션과 오리엔테이션 에러를 최소하하는 방법
• end effecter 부터 시작을 하고 toor joint를 향해 나아가며 각각 joint는 이 end effecter가 최대한 타겟 포지션과 가까이 있을 수 있는 방향으로 움직임
• 만족할만한 결과가 나올 때까지 반복한다
• 엄청나게 빠르다!

🖤Triangulation IK

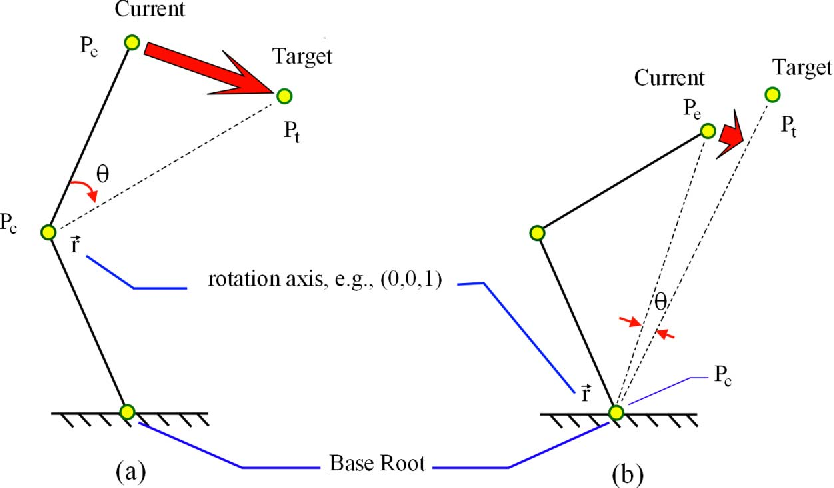
Law of Cosines for IK

• Triangulation Inverse Kinematics approach uses the cosine rule to calculate each joint angle starting at the root of the kinematic chain moving outward towards the end effector.
  root부터 시작을 해서 kinematic chain을 따라 바깥쪽으로 향한다.
  

• unconstrained joints를 사용했을 때 + 팔이 닿을 수 있는 거리 ⇒ 항상 답이 나옴
• Triangulation algorithm이 사용된다.
  → CCD algorithm보다 더 빠르게 low const로 해를 찾는다. 딱 한 번의 iteration으로 구한다.
  

1. 시작지점을 정한다
2. 루트로부터 첫번째 조인트를 a 나머지를 모두 b로 둔다. 코사인 법칙을 이용해서 풀면 풀린다.

문제는.. However, the results are not realistic.

이상한 결과가 나온다. 실제적이지가 않다.

• end effector 근처에 있는 조인트는 straighr line이다.
• end effector가 하나일 때만 제대로 작동, 여러개는 한번에 적용 불가
• complex한 character model에는 사용 불가
• constraints 가 있으면 답을 풀 수 없다
  → 내 관절은 몇 도 이상 꺾이면 안 돼. 이런게 있으면 풀 수 없다.
  

🖤Sequential Inverse Kinematics

Sequential Analytic-iterative IK

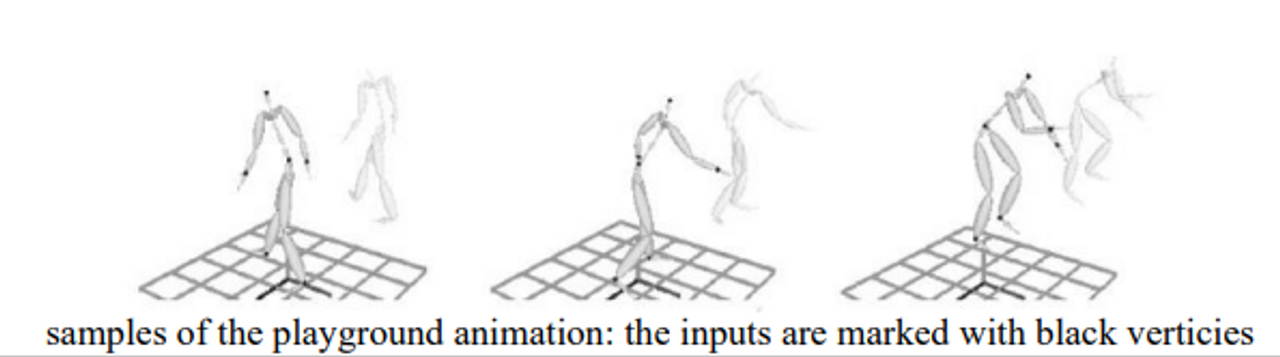
• 실시간의 3d human full-body movements를 reconstruct할 수 있다.

  → The inputs to this method are end effector positions, such as wrists, ankles, head and pelvis (the least possible input in order to be usable within a low-cost motion capture system in real-time), which are used to find the human pose.

  → input이 하나가 아니라 여러개의 end effecter의 포지션이다.

  → 그림에서 점들이 모두 입력으로 들어온 것

  → VR에서 보통 사용하는 느낌이다. 머리 팔 다리 루트의 포지션이 들어오면 다른 joint들의 포지션들을 구하는 것. 앞에 알고리즘 보다 조금 더 clue가 많은 상태이다.
  

The procedures are as follows:

1. The orientation of the root joint is estimated from the known positions.

   루트 조인트를 결정을 한다. 보통 허리 pelvis

2. The configuration of the spine is found using a hybrid IK method that combines this estimated orientation with the positions of the root and head markers.

   헤드와 루트를 이어 척추를 만든다.

3. Then the orientations of clavicles are determined with the positions of their known end-effector positions and the already positioned spine.

   어디를 바라보고 있는지 방향을 설정한다.

4. Finally each of the limbs(팔 다리) is situated according to their known end-effector positions.

   팔 다리를 대충 그린다.

---

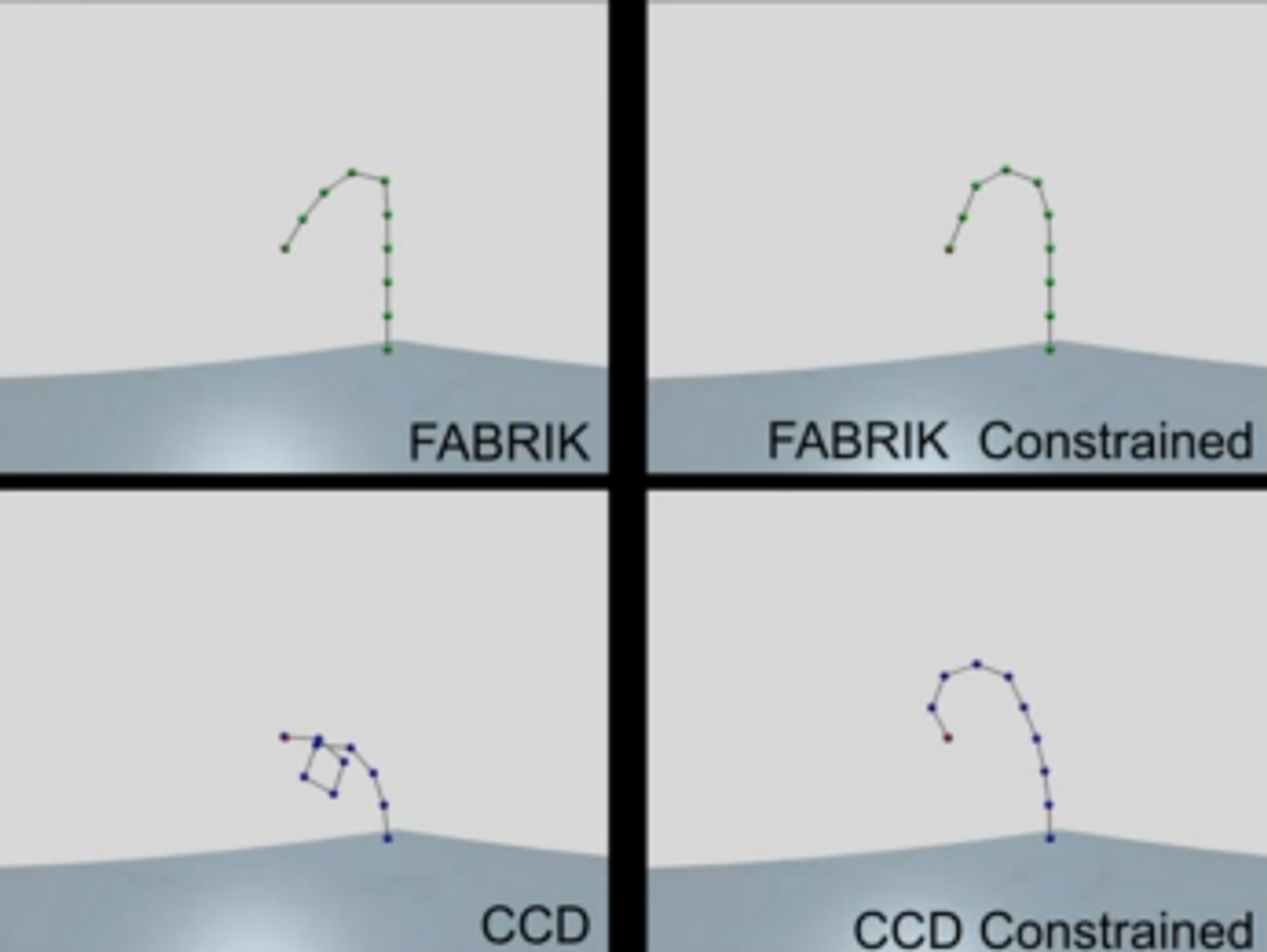
🖤FABRIK

A fast, iterative solver for the Inverse Kinematics Problem

• Forward and Backward Reaching Inverse Kinematics (FABRIK)
• 초 강력자! 언리얼도 이 알고립즘을 사용한다.

• joint가 연결이 되어 있을 때 어떤 알고리즘은 뒤에서부터 앞으로 어떤 것은 앞에서부터 뒤로 갔는데 패브릭은 이 두개를 모두 사용한다.

  →앞으로도 뒤로도 iterative하게 돈다
  

• 시스템 에러를 minimize하는 알고리즘이 들어간다.

• 엔드 이팩터부터 시작을 하고 하나하나 역으로 거슬러 올라오며 에러를 줄이는 방향으로 한 번에 한 조인트씩 조작을 가한다.

• 그 다음에는 반대 방향으로 돌아와 full iteration을 돈다.

• 로테이션 관점에서 생각하는 것이 아닌 포지션 관점에서 생각한다.

• it converges in fewer iterations, has low computational cost, and produces visually realistic poses.

• 회전하는 것이 쉬운 개념은 아니었다. 포지션을 바꾸는 것이 더 쉬운 개념이다. 때문에 심플하게 문제가 풀린다. rotation을 바꾸는 것은 쿼터니언이더라던지 지오메트릭 알지브라 라던지 복잡하기 때문이다.

  ⇒ 그래서 휴리스틱 알고리즘에서는 포지션을 수정해 풀게 된다.
  

• FABRIK has been integrated in several game engines, including the Unreal Engine, Unity3D, and Panda.

Before explaining the procedure, let’s define several parameters

• p1 : root joint
• pn : end effecter

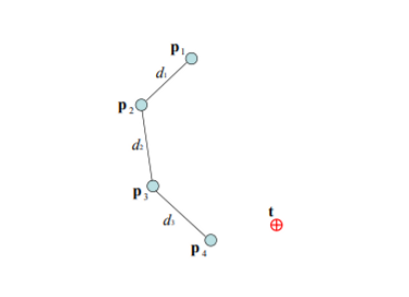
The procedures are as follows

1. Calculate the distances between each joint $d_i = 𝑝_{𝑖+1} − 𝑝_𝑖$ , for i = 1, ..., n-1.
   각 joint의 distance를 구한다. bone의 길이

2. Check whether the target is reachable or not; find the distance between the root and the target, and if this distance is smaller than the total sum of all the inter-joint distances, the target is within reach, otherwise, it is
   unreachable.
   타겟이 reachable 한지 안니지 확인한다. root와 타겟 사이의 거리가 각 bone의 길이보다 작으면 닿는다고 한다. 이걸 먼저 체크한다. 닿는다고 하면 그때 계산 시작한다. (만약 닿지 않는다면 그냥 쭉 핀다)
   

3. If the target is within reach, a full iteration is constituted by two stages.

   타겟에 닿을 수 있으면 full iteration(back + forward)를 돈다.

4. In the first stage:

   1. end effecter로부터 시작해 joijnt positon을 결정하느데 pn부터 시작해서 p1방향으로 한 번씩 돈다
   2. p4를 일단 그냥 타겟 포지션으로 옮긴다.
   3. p4와 p4’을 지나는 l_n-1을 구한다
   4. p4’의 새로운 포지션을 구했다. d3크기만큼 되는 위치에 p3를 둔다
   5. 그리고 이를 반복 한다
   6. 그러면 다했을 때 root가 움직이는데 이제 root를 타겟 포지션으로 삼아서 반대로 한 번 더 한다.

📌 FABRIK with Multiple End Effectors

In reality, most of the multibody models, such as hands, human or legged bodies etc., are comprised of several kinematic chains, and each chain
generally has more than 1 end effector.

• 몇개의 kinematic chain 으로 이루어져 있고 보통 1개 이상의 end effecter를 가지고 있다.

• multiple end effecter와 multiople target problem을 풀 수 있어야 한다.

• FABRIK can be easily extended to process models with multiple end
  effectors
  - 사전 정보가 필요하다
  - sub-base joint: 2개 이상의 체인이 연결되어 있는 곳
  ex) pelvis
  

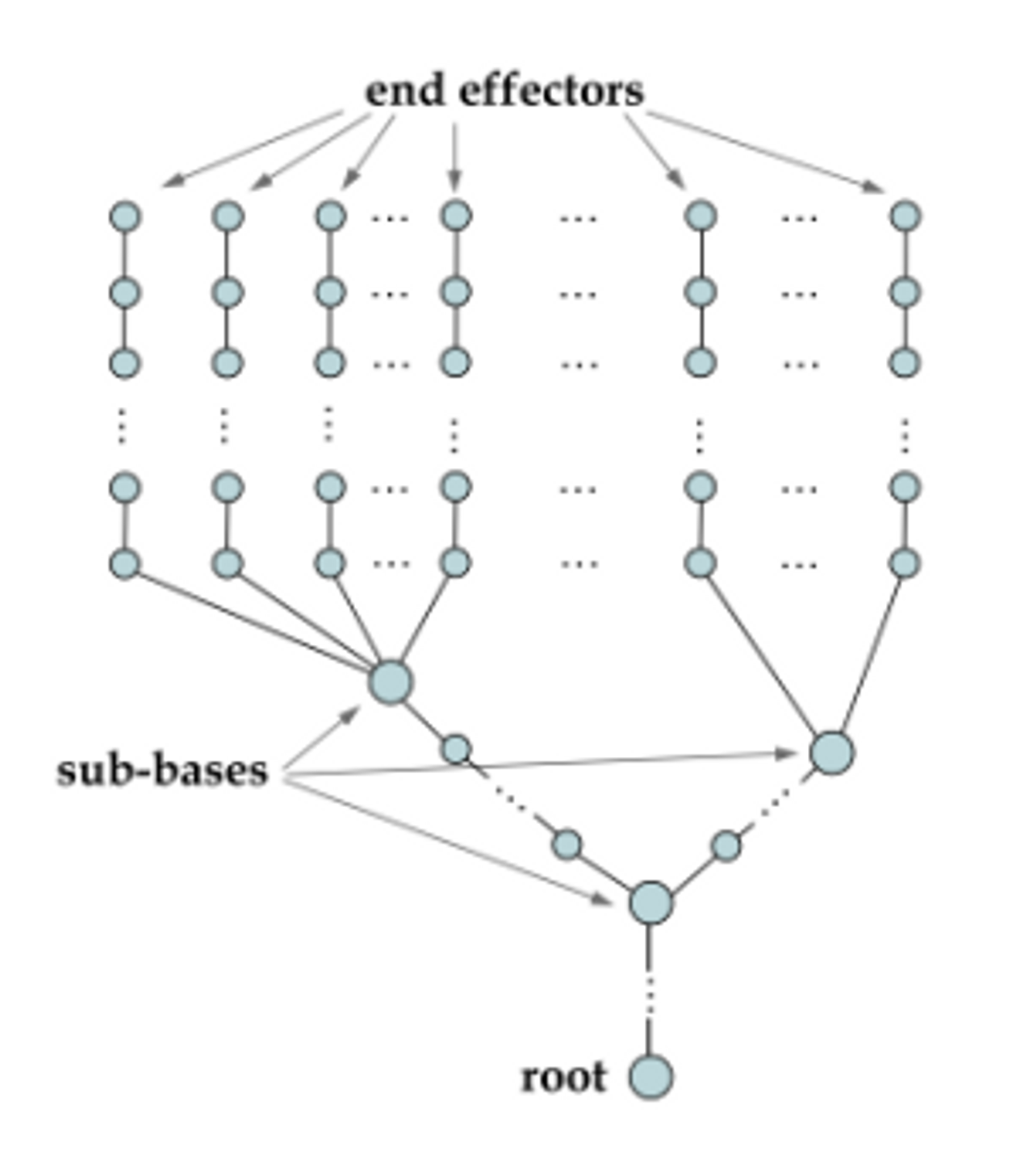
The algorithm is divided into two stages, as in the single end effector case.

First stage

1. 엔드 이팩터부터 시작을 하는데 parent sub-base까지만 간다. root까지가 아니라
2. 따로 풀었기 때문에 두개의 입장에서 parent sub-base의 위치가 다를 수 있다
3. 여러개를 average을 낸다.
4. sub base로 부터 root까지 다시 푼다.

Second stage

1. root부터 sub base까지
2. 그냥 root의 위치를 원래 있어야 하는 위치로 강제 고정 시키고 나머지를 옮긴다. 만약에 sub base 여러개 되면 average을 낸다.

📌FABRIK with joint limits (constraints)

joint constraint를 고려를 해야 한다.

앞에서 직선으로 옮기고 이런것 했는데 이때 옮긴 joint의 세타가 constraint를 만족하지 않을 수 있다.

• 실제와 같은 바디 모션을 만들기 위해서 joint들은 가동 범위라는 것이 정해져 있다.

• Since FABRIK is iterative
  → joint restrictions 각 스템마다 고려를 해준다.
  

• main idea
  → joint constraint를 지켜줄 수 있는 bound 내로 re-positioning and re-orientation of the target 해준다.
  

• 대다수의 존재하는 테크닉과 비교했을 때 3d에서 고려하는 문제를 2d로 가지고 와서 풀기 때문에 cost가 줄어든다.

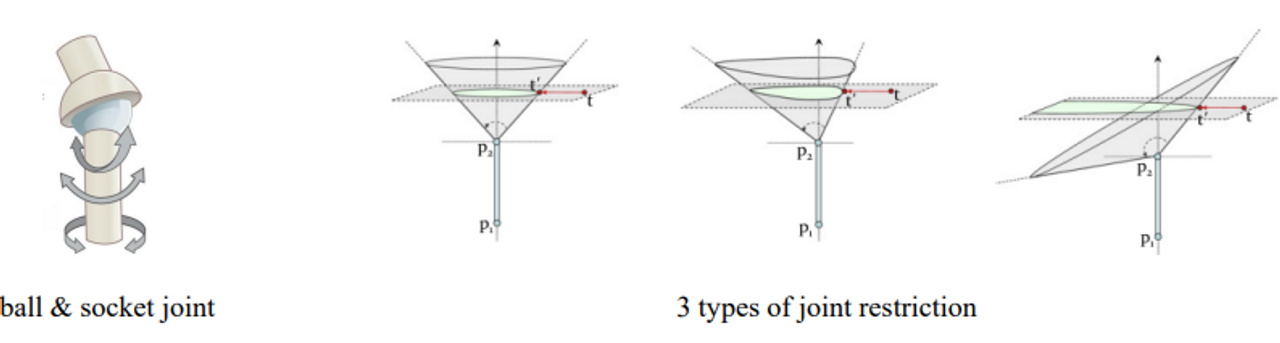
• Assume we have a ball-and-socket joint with orientational limits described by the rotor R and rotational limits described by the angles θ1, ..., θ4

• irregular cone의 형태로 a joint limit boundary 가 정해진다
  → 우리 joint가 모두 같은 restriction을 가지지 않기 때문에 온전한 콘의 형태가 아니라 조금 찌그러진 콘의 형태가 된다
  

• 보통은 3개의 conic section

1. If all θs are equal, the conic section is a circle.

   자르면 원의 형태

2. If there are θs are greater or smaller than 90 and are not equal, then the conic section has an ellipsoidal shape.

   자르면 타원 형태

3. If there are θs both greater and smaller than 90, then the joint boundary limits are defined by a parabolic
   shape.

⇒ 자를때 이전 조인트의 수직을 자름

• 편의를 위해 ellipsoidal shape라 가정을 한다 (실제로 대부분 이것임)

  → 가장 일반적인 케이스이기 때문에 이거 알면 된다.
  

• 3d에서 2d로 바꾸면 아래 그림과 같다
  → 타원 모양을 2d로 가지고 옴

  → t 와 t’의 거리를 최소화 시키는 점을 찾는다
  

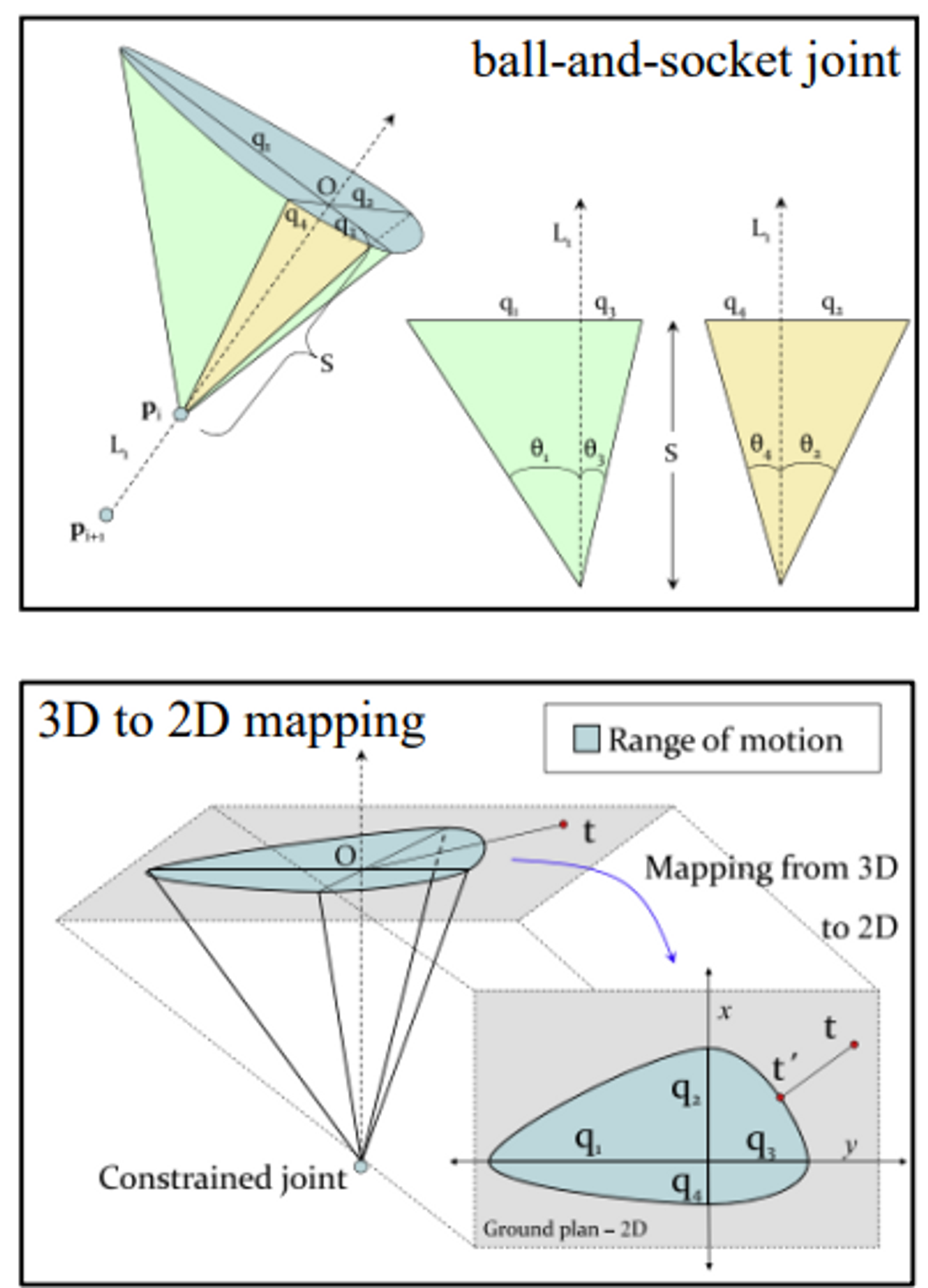
The orientation of the joint can be assigned as follows:

• end effecter의 위치를 타겠으로 옮긴 상황에서 p3’의 위치를 정해야한다.
  이전에는 직선을 그어서 본길이에 두었다.
  
• 가능한 위치인지 확인하고 가능한 것이면 가지고 온다.

• rotatitianl limit를 세타 1- 세타 n

1. 타깃과 O를 잇는 선에서

2. S를 결정한다. O와 p_i 사이
   q_j를 구한다

3. O가 원점에 위치하도록
   바운더리가 3차원 공간상에 정의되어 있는 것을 그냥 풀기에는 cost가 크니 2d문제로 바꾸려 한다. O를 원점으로 하는 xy 평면 위에 올려 놓고 문제를 풀기 위한 과정이다.

4. motion range(관절체의 가동 범위) 안에 타깃이 없을 때 가장 가까운 곳으로 가동 범위 안에 옮겨준다

5. 어느 사분면에 있는지 정해지면 어떤 값을 구해야하는지 알 수 있다

   → 코스트를 줄이기 위한 기묘한 방법들....

Incorporating rotational and orientational constraints within FABRIK

• p4를 target으로 끌고 오는데 포지션 뿐만 아니라 오리엔테이션도 바꾸어서 끌고 온다.
• 그 다음 p4와 p3를 쭉 이어서 본 위치로 끌고 온다
• p3’가 그냥 끌고 왔기 때문에 오리엔테이션이 이상하다.
• p3’을 motion range 바운드에 있도록 하는 오리엔테이션으로 바꿔 준다.
• 원래 p3’와 p2를 연결해 직선 거리에 끌고 왔어야 했는데 지금 range에 벗어났다. 그래서 그 range에서 가장 가까운 위치로 p2’를 끌고 온다. 그리고 리오리엔테이션을 해준다.

⇒ constraint가 걸린 친구도 잘 풀 수 있게 된다.

FABRIK produces visually the smoothest and most natural movements than previous IK methods
기존에 사용한 것보다 훨씬 좋다.

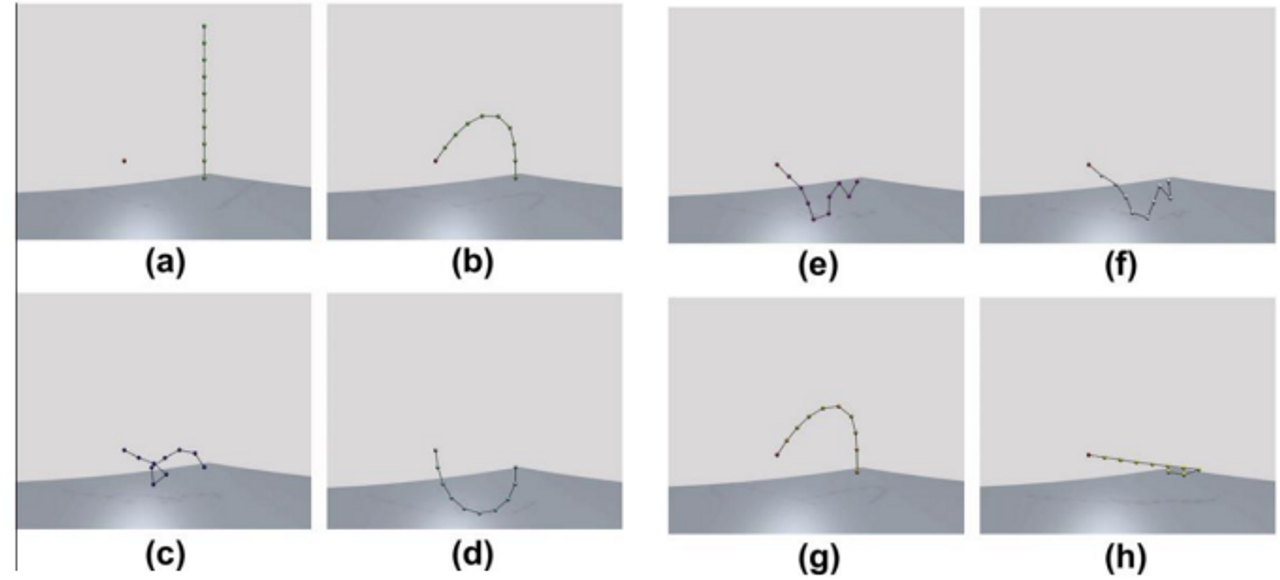
(a) Initial position, (b) FABRIK, (c) CCD, (d) J. Transpose, (e) J. DLS, (f) J. SVD-DLS, (g) Follow-the-leader, (h) Triangulation

FABRIK produces results significantly faster than all IK methods tested.

• CCD보다 10배 빠름
• 자코비안 based 보다 1000배 빠름
• FABRIK has the lowest computational cost and, at the same time, produces visually the smoothest and most natural movements.
  사람이 하는 것처럼 최소한의 힘을 들여 가는 것이 잘 표현.
  
• 적은 iteration + 목표 위치로의 빠른 수렴 + unreachable 해도 타겟을 향해 가까이 가는 것도 가능

---

🖇 Reference

해당 포스트는 강형엽 교수님의 게임공학[GE-23-1] 수업을 수강하고 정리한 내용입니다.