
Visualizing Images
- pixel 한 개가 담을 수 있는 정보의 범위는 크다
→ 소가 멀리 있으면 소의 머리 전체가 한 픽셀일 수도 있고 가까이에 있으면 눈 하나가 픽셀 하나일 수도 있다.
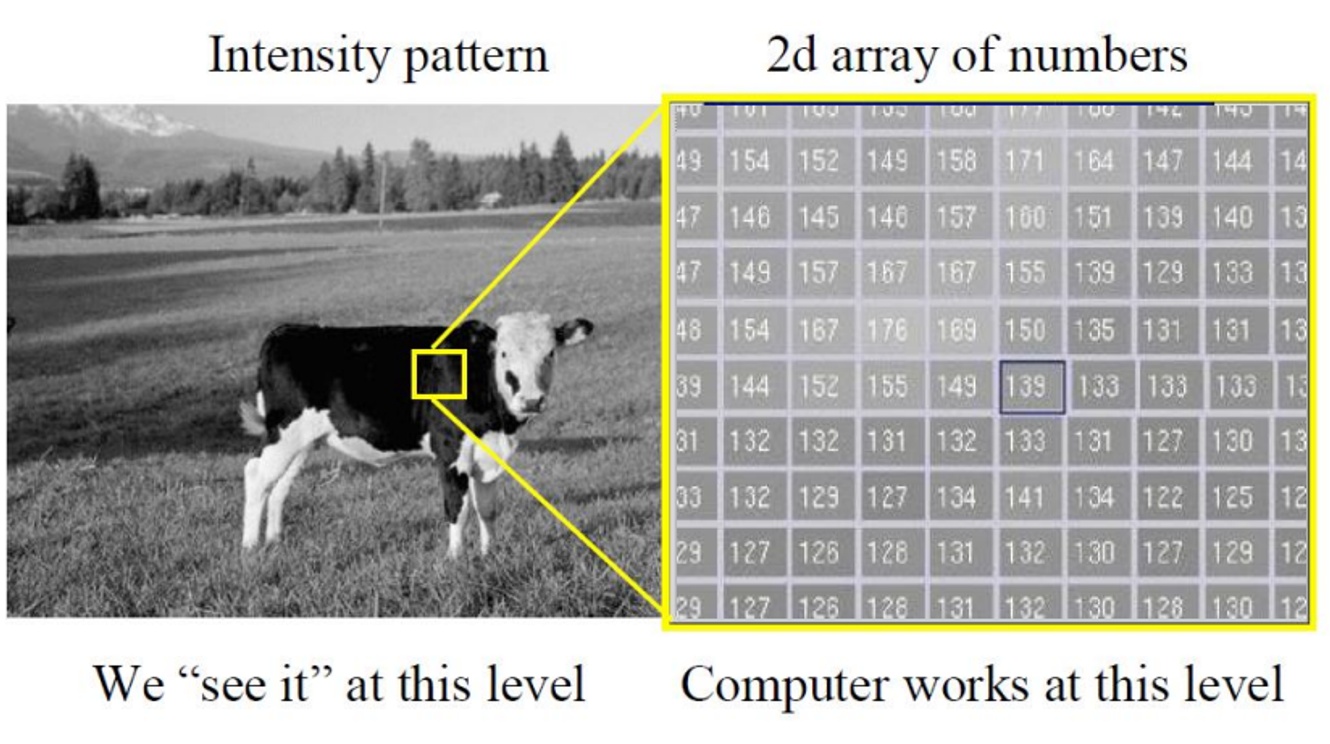
Image as Surfaces
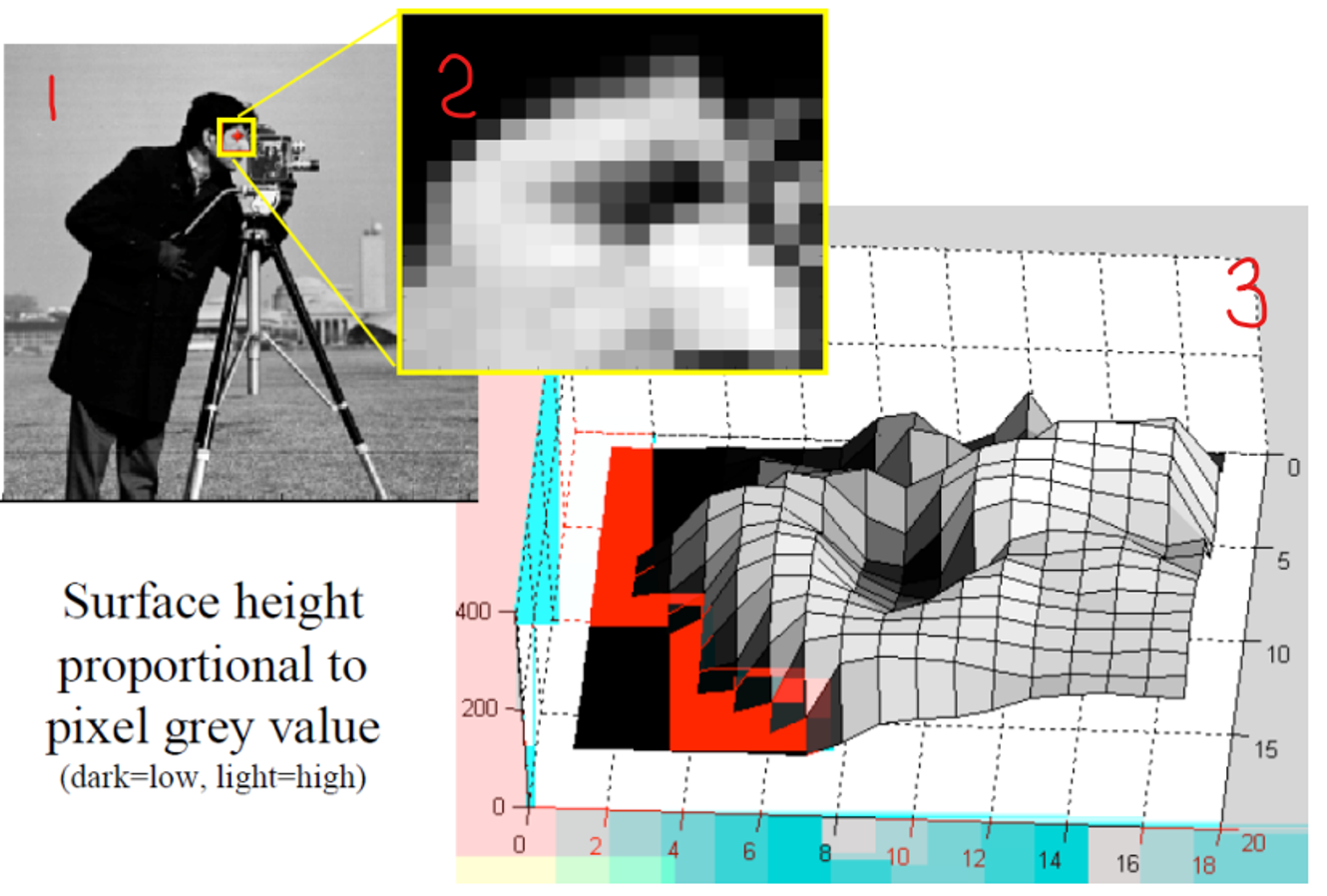
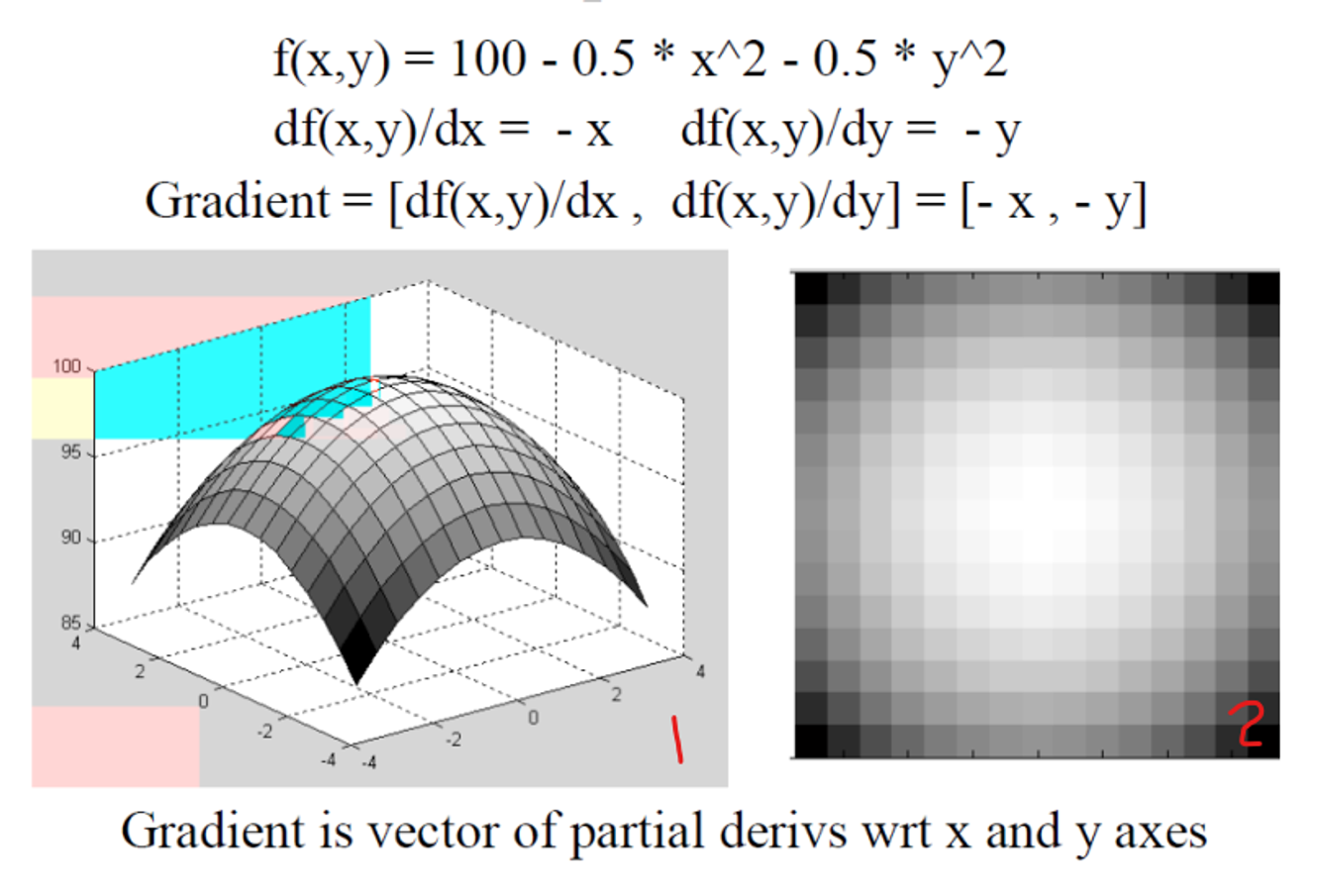
1번 사진→2번 사진을 떠올리는 것을 잘 할 필요가 있다.3번 사진
y 축 높이가 높게 표현될 수록 밝기가 높은 것을 볼 수 있다. 즉 2차원에서의 밝기가 그림 3번에서는 3차원의 높이로 표현이 되었다.
Example
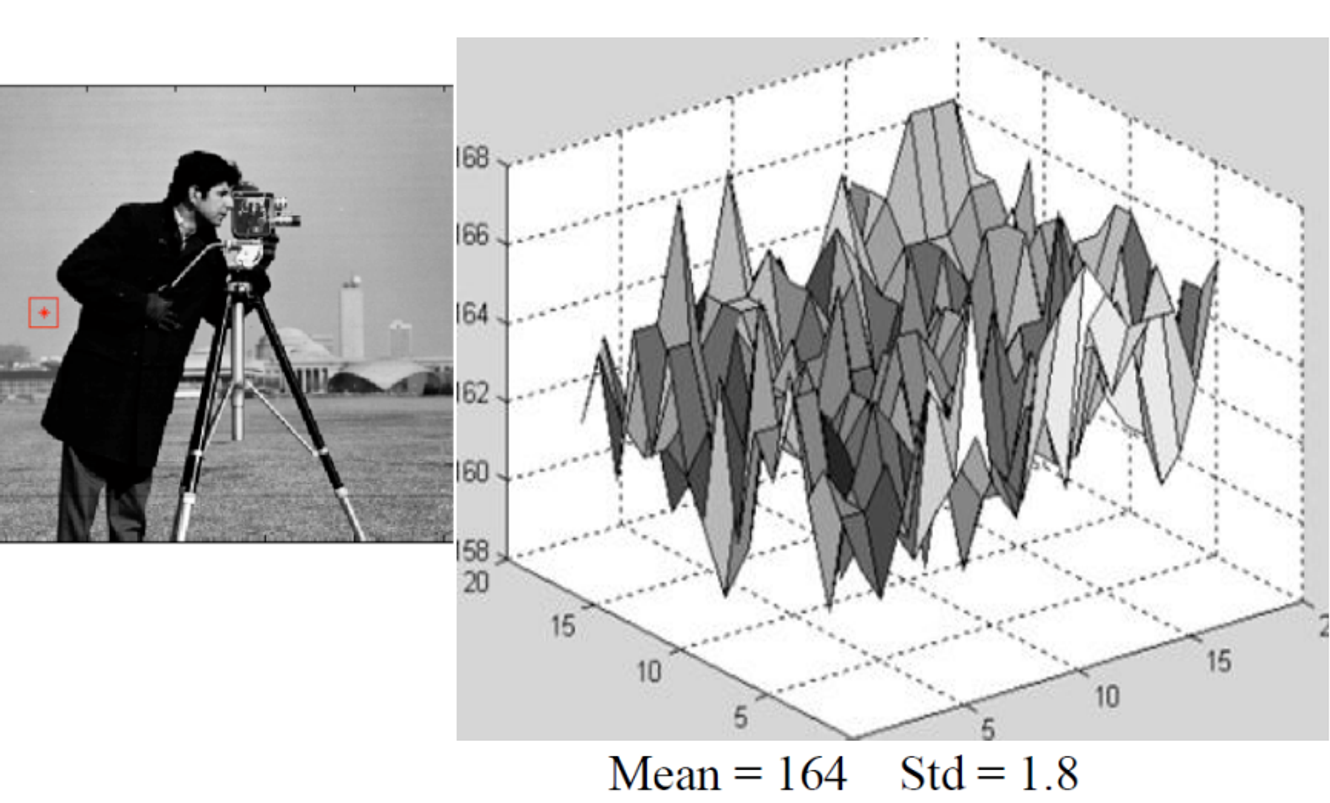
거의 밝기가 비슷하기 때문에 값이 거의 비슷하고 변화가 거의 없다.
하지만 왼쪽 사진을 보면 빨간부분이 밝기의 변화가 거의 없기 때문에 왼쪽그림에 삼차원으로 표현했을 때 기울기가 거의 없어야 하지만 기울기가 존재한다. 이는 noise때문이다.
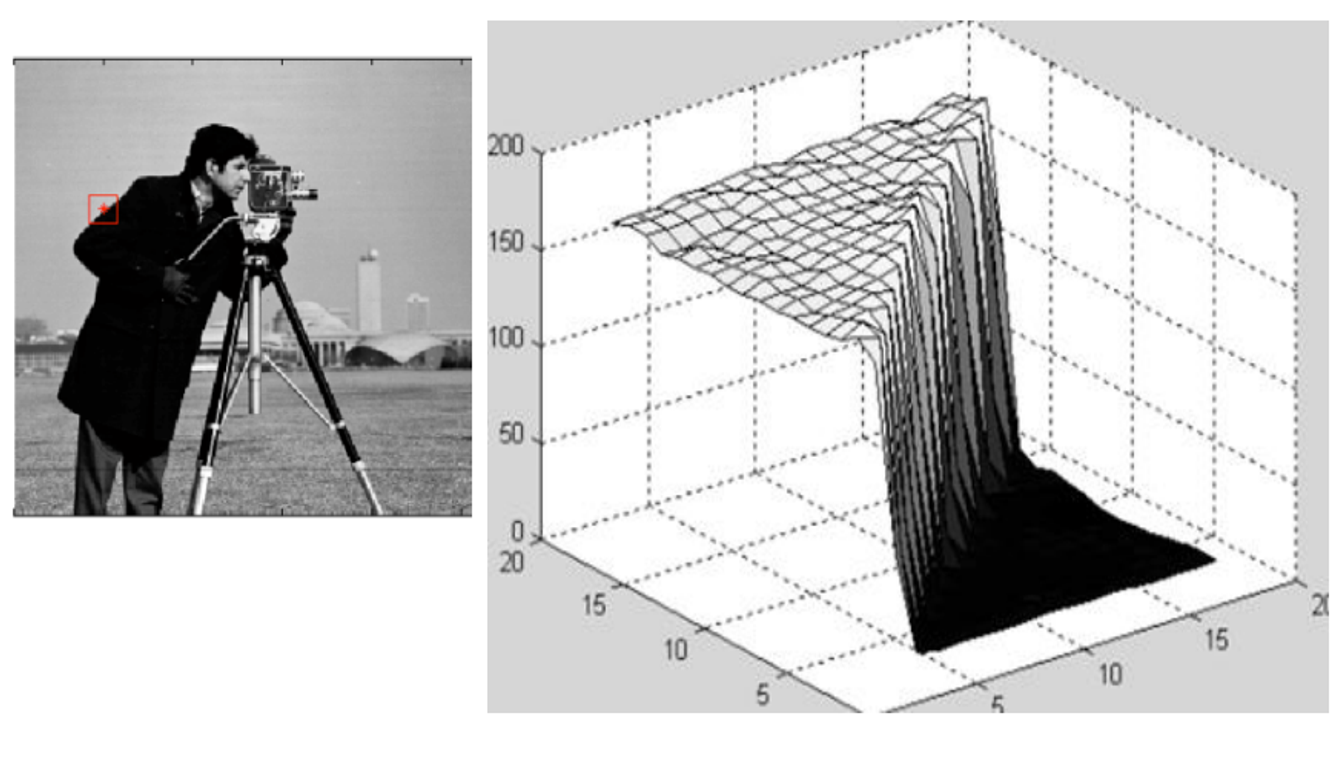
이번에는 왼쪽 그림에서 변화가 심하기 때문에 오른쪽에서 3차원의 모양이 거의 절벽처럼 나온다. 즉 형상의 변화가 심하고 기울기의 변화가 심한 것을 알 수 있다.
이처럼 이차원의서 밝기 변화를 3차원에서 높이 변화로 표현할 수 있다.
Gradient
✔ 1D Gradient
제일 쉬운 것부터 시작해보자.
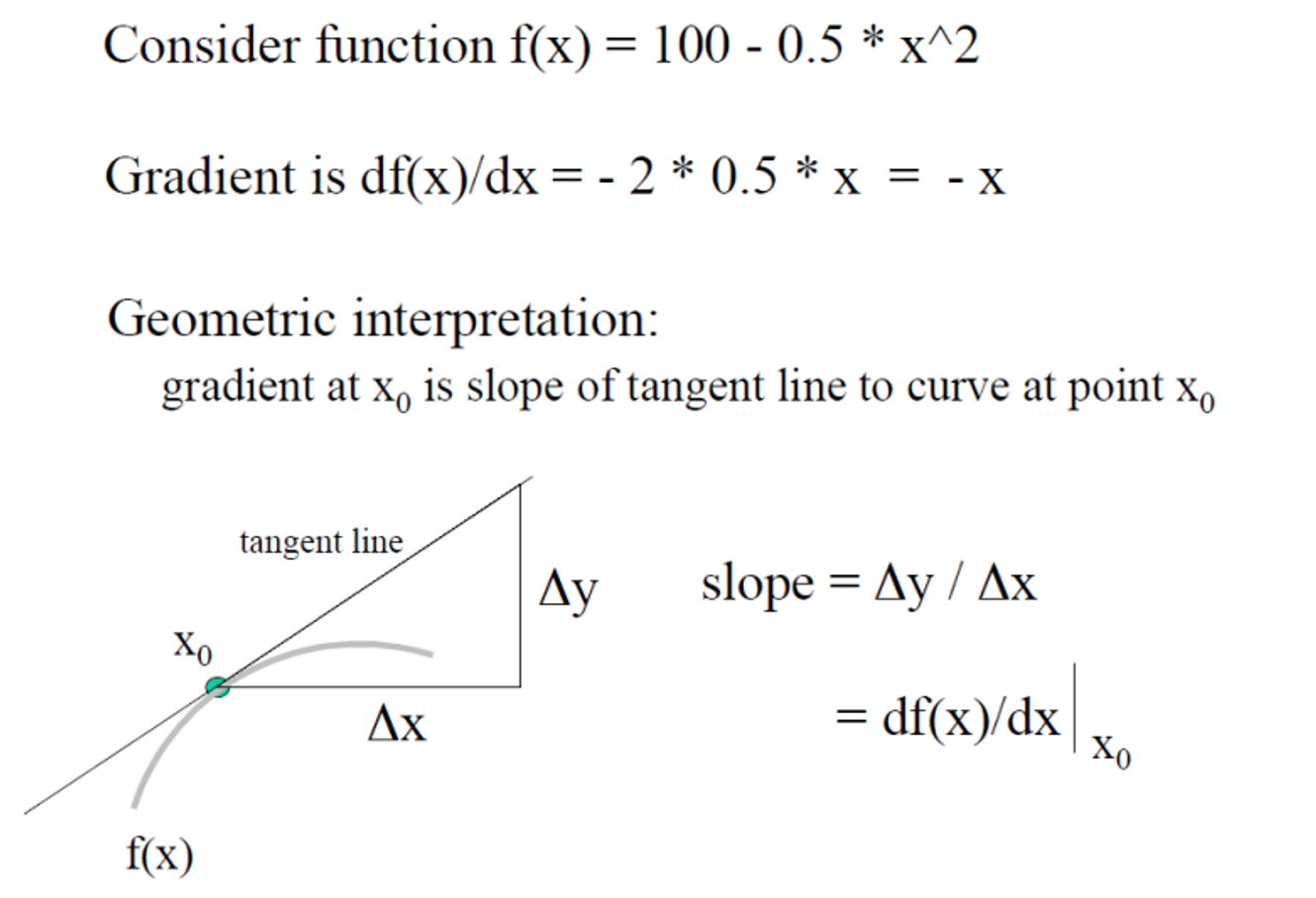
우리는 수학 시간에 평균 변화율, 순간 변화율을 구했다. 그렇지만 거의 순간 변화율만 사용을 한다. 하지만 우리는 이제 다시 평균 변화율로 돌아올 필요가 있다! 이제 우리는 수능 문제를 푸는 기계가 아니니 직접 데이터를 관측해서 구해야한다. 아무도 우리에게 수식을 쥐어주지 않는다.
결국 구하고자 하는 것이 어떤 순간의 변화율이어도 우리는 평균 변화율이 필요하다. 왜냐면 구하는 과정에서 approximation이 들어가 error가 존재하기 때문이다.
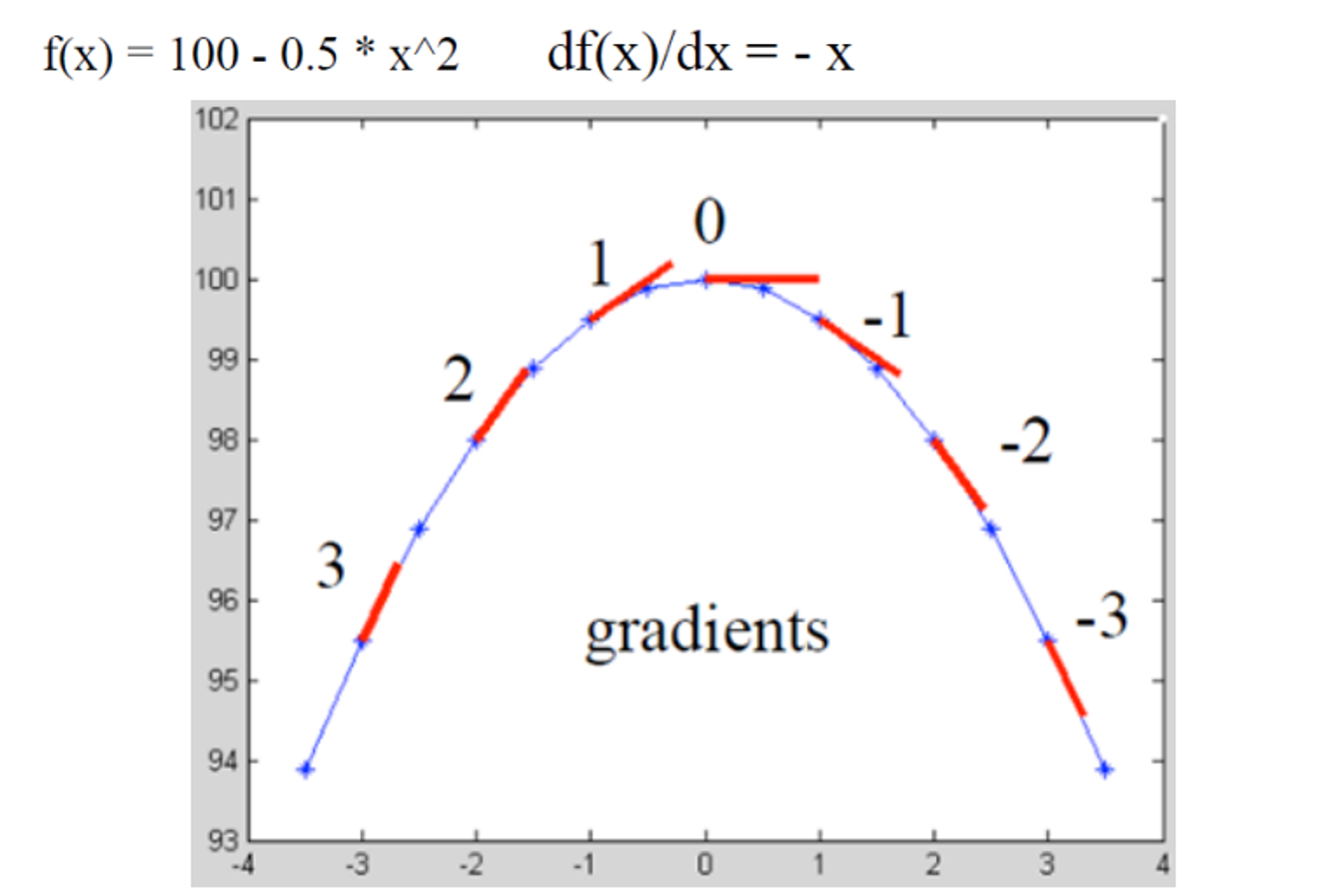
✔ 2D Gradient
사진에 표현된 화살표가 모이는 곳이 꼭대기 시작 부분이 끝에 해당한다. 이때 꼭대기 peak 지점에선 gradient는 0이다.
산을 오르고 내려가는 상황을 가정했을 때 3번 그림에서 동그라미 선은 등고선(=등밝기선 =등intensity선)이다. 빨간선을 따라가면 산을 올라가게 되고 파란선을 따라가면 산을 내려가게 된다.
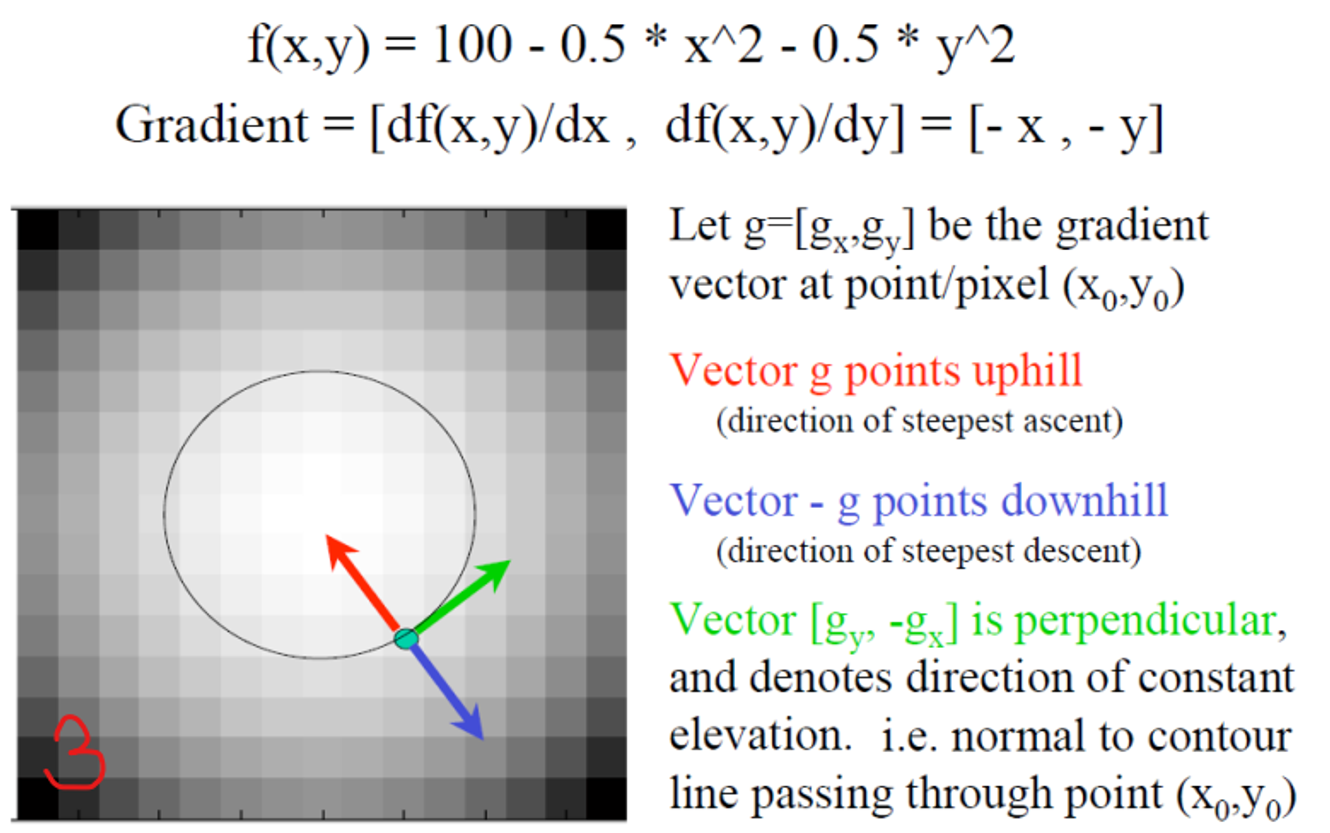
Image Gradient
- 화살처럼 gradient를 구할 수 있다.
- 등고선처럼 isolation이 발생하는 부분이 나중에 중요하게 적용될 수 있다.

Numerical Derivatives
우리는 지금 함수의 일차 미분
f'(x)를 구하고자 한다.아는 정보는
f(x+h),f(x)두 개이다.
-
Finite forward difference
일차 미분을 구하기 위해
f(x+h),f(x)을 사용한다. 테일러 시리즈 급수를 이용해 이차미분 이후 모르는 부분은 다 생략해버린다. 이게 이제 노이즈, 에러가 된다.최종식을 보면
O(h)가 에러가 된다. 이런 식으로 구할 수 있다.

- Finite backward difference

-
Finite Central difference
놀랍게도 1번 2번보다 3번이 더 정확하다.
- 명시적인 이유
가운데와 왼쪽, 가운데와 오른쪽이 아닌 가운데를 기준으로 왼쪽 오른쪽 값으로 구하기 떄문에 더 멀리 보아 지엽적인 상황에 둔감하기 때문이다
- 수학적 이유
실제로 1,2 번 식에서는 를 그냥 지웠지만 여기서는 두 식을 빼는 과정에서 자연스럽게 사라진다. 억지로 지운 값(error)이 줄어듬으로 더 정확해지는 것이다.
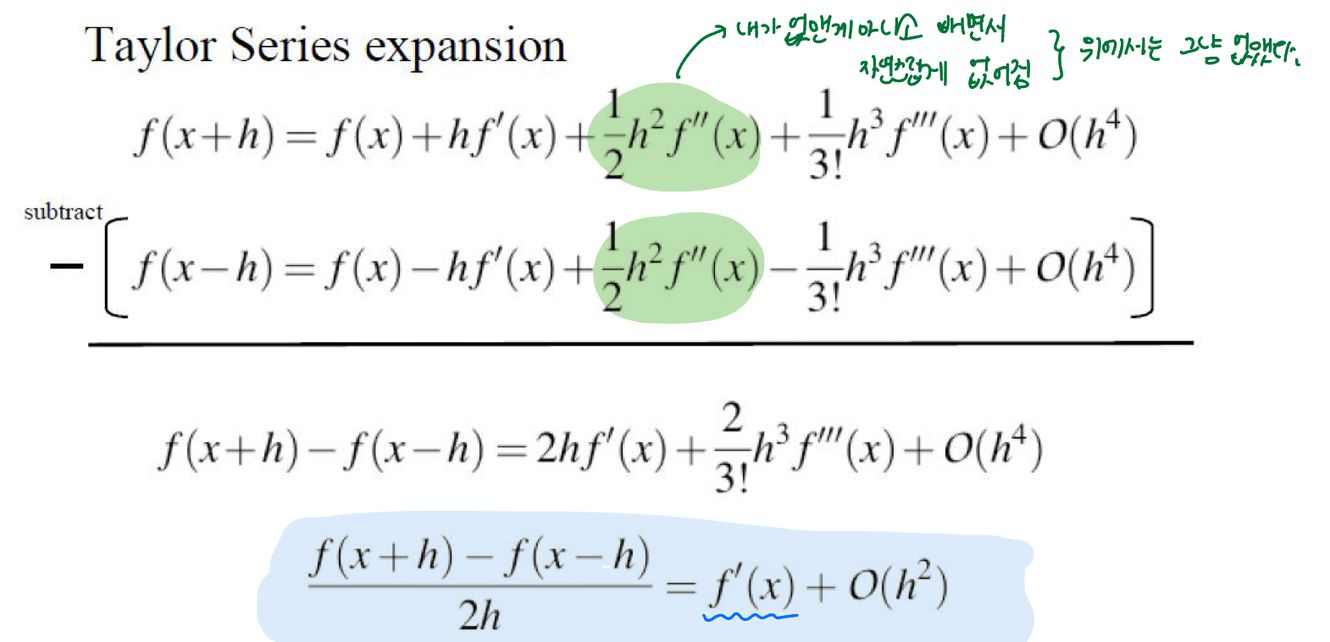
- 명시적인 이유
💡 Numerical Derivatives
일차 미분을 구하고자 할 때.
Example : Spatial Image Gradients
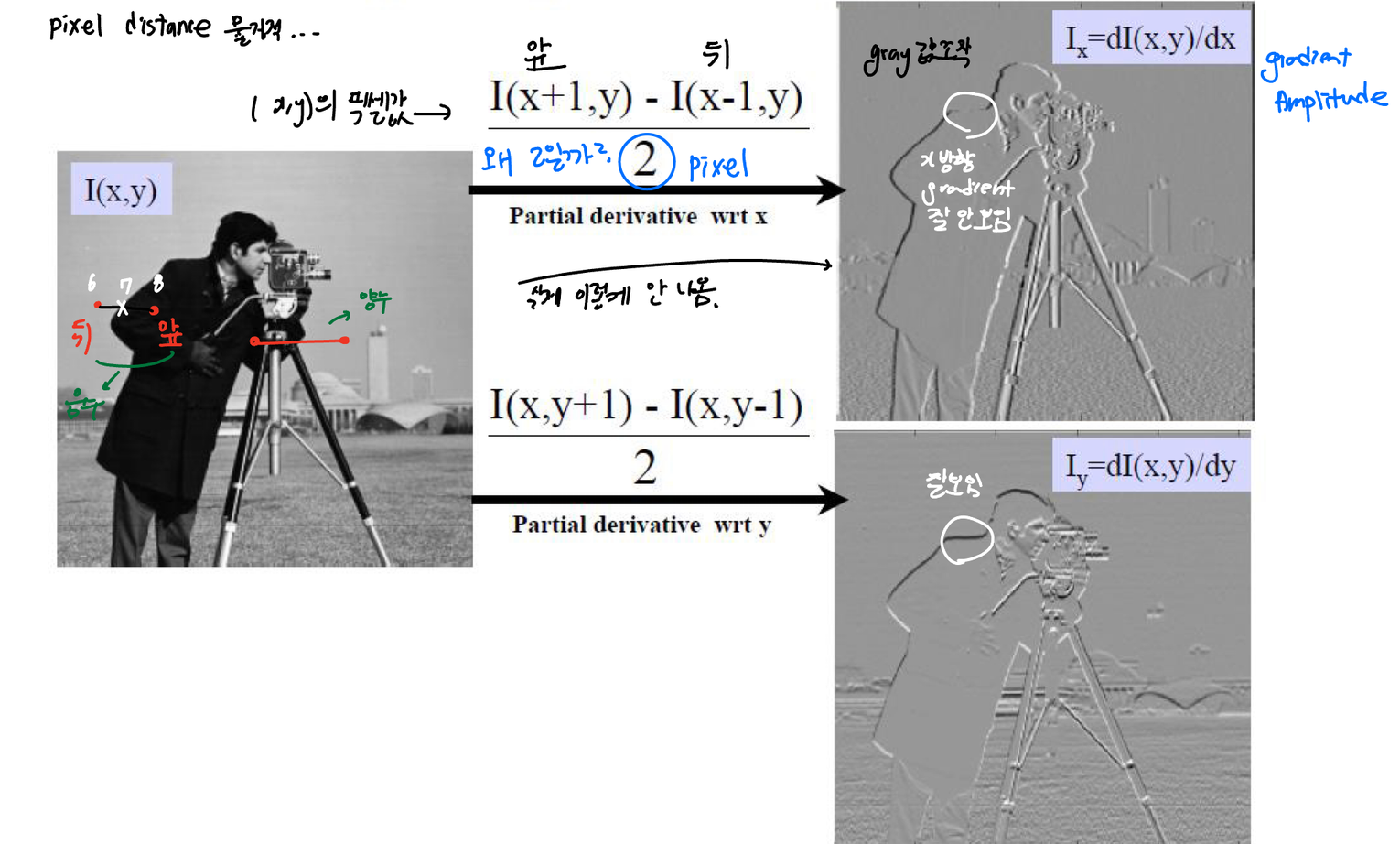
왼쪽그림 6,7,8을 픽셀이라고 가정했을 때 남자의 팔 부분은 음수이다. 오른쪽(앞)이 더 어둡고 왼쪽(뒷부분)이 더 밝기 때문이다. → 7픽셀에서는 gradient가 음수 값을 갖는다.
그렇게 gradient를 구했더니 오른쪽 첫번째 그림에서는 x축 방향으로의 gradient를 구해서 x 방향 gradient가 잘 보이지 않았다. 이에 y방향 gradient도 구해 이 둘을 합쳤다.
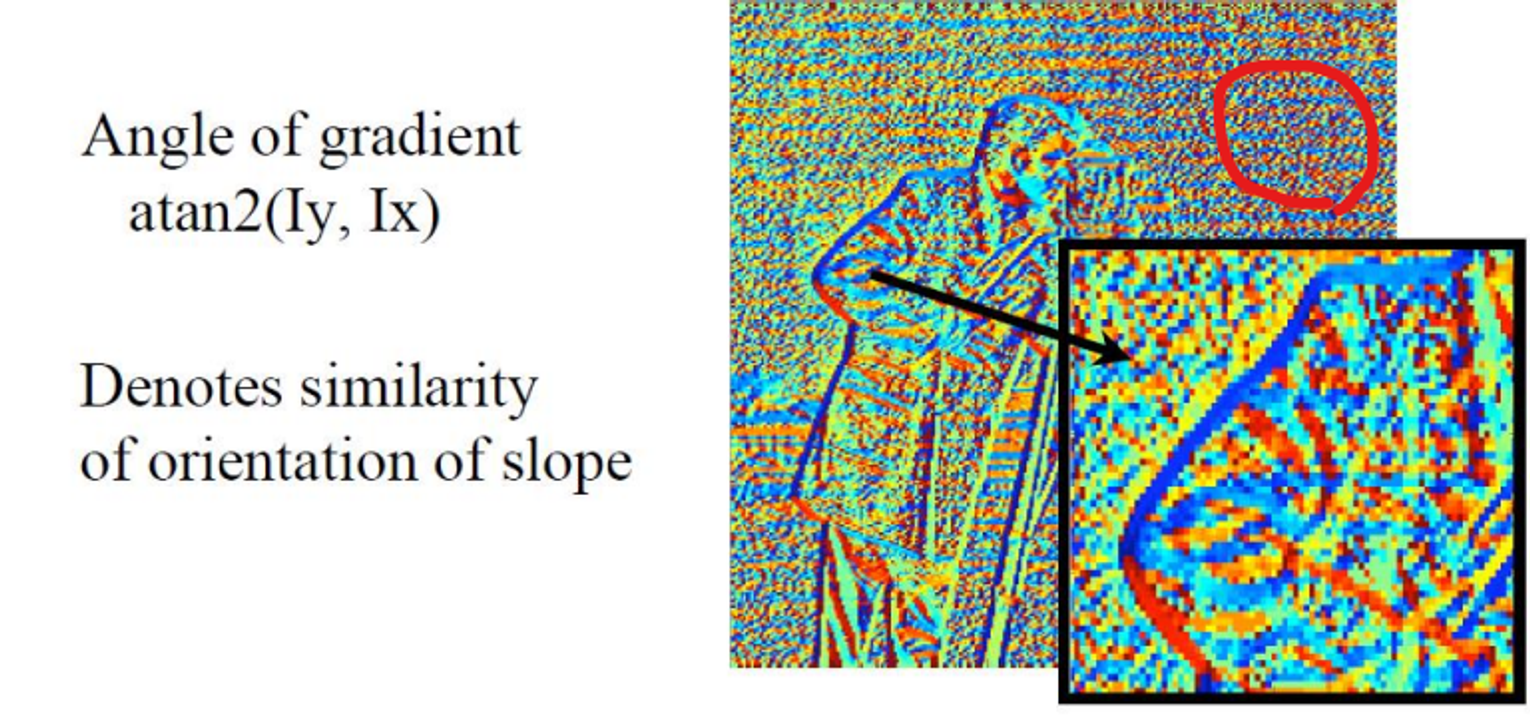
이 사진은 orientation을 Color로 나타낸 것이다.
빨간 동그라미를 친 부분은 원래 amplitude가 거의 0에 가까워 균일해야하는데 굉장히 지저분하게 표현이 되어 있다.
이는 아주 작은 amplitude가 있지만 orientation을 각각 존재하고 noise가 존재하기 때문에 이처럼 보인다. 그렇기에 Noise를 제거하는 과정이 필요한 것이다.
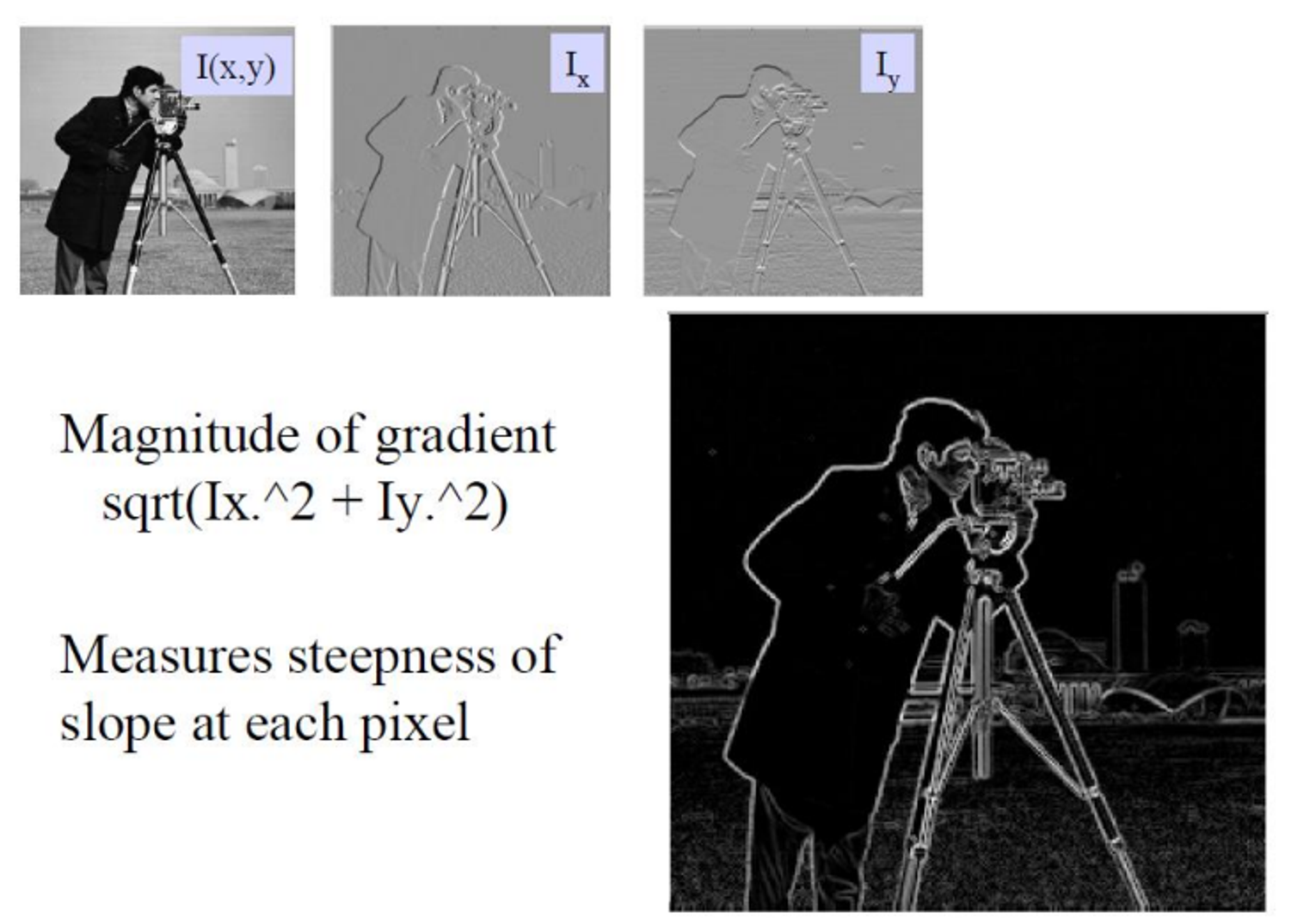
Functions of Gradient
✔ 3D gradient
3차원 gradient도 존재한다. t축으로 구할수는 있으나 큰 의미를 가지고 있진 않다. z축과는 갖는 의미가 다르다.
그러나 동영상에서는 조금 상황이 달라진다. t축이 하나 더 생기면서 3차원이 되면 아래 사진처럼 t축에 따라 한 픽셀이 시간에 따라 변화학는 것을 볼 수 있다.

✔ more specifically
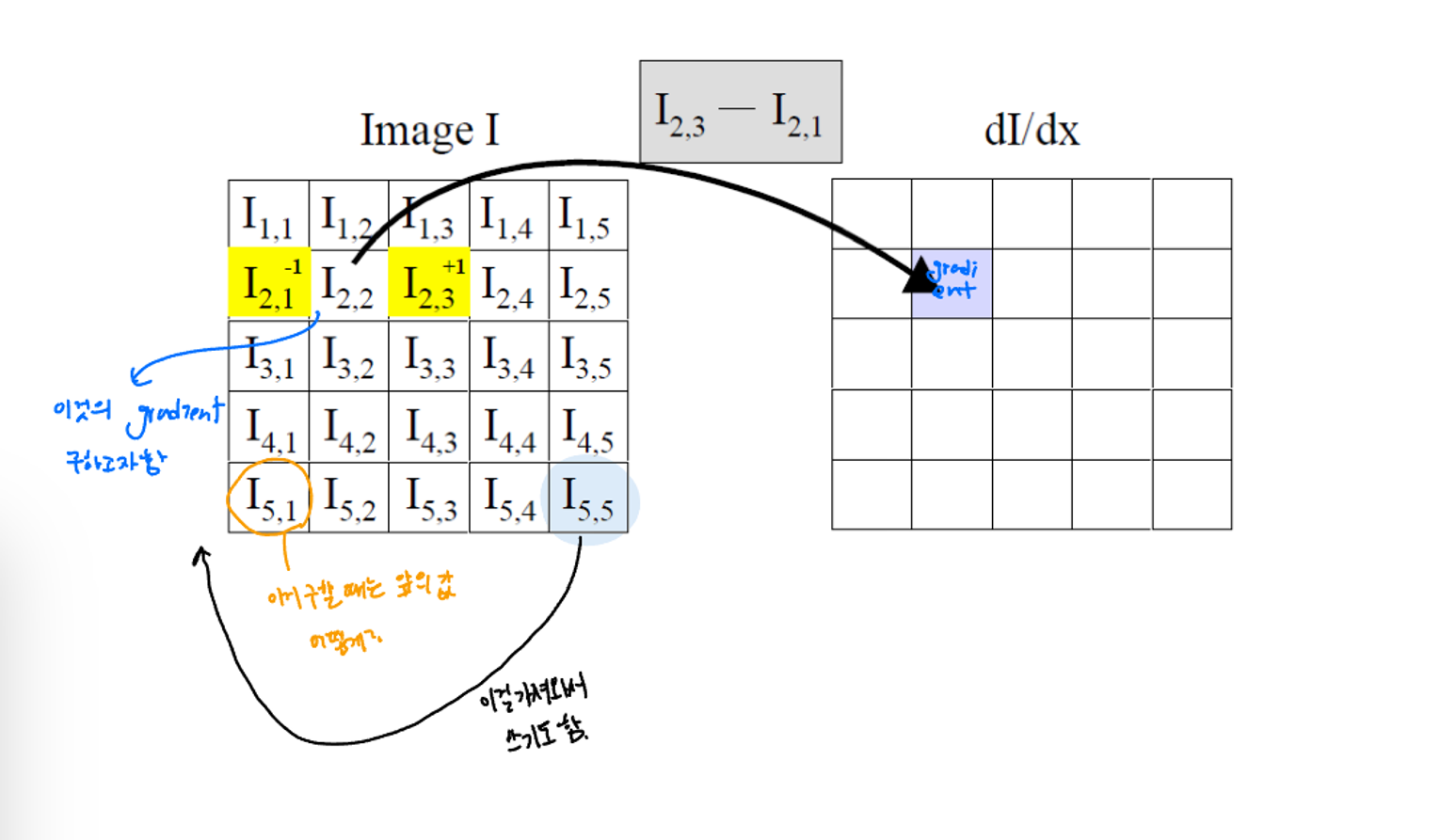
아래 사진처럼 있을 때 I_(2,2)의 그래디언트를 구하고자 한다. 그러면 양 옆에 있는 I를 이용해 그래디언트를 구할 수 있다. 그런데 만약에 끝에 있는 픽셀의 그래디언트를 구할 때는 어떻게 할까? 여러 방법이 있지만 아래 사진처럼 반대쪽 끝에 것을 가져와 쓰기도 한다


우와 너무 흥미있어 보이네요. 저도 듣고 싶어요! 좋은 글 감사합니다 ^^~