🔗강의 영상

목차

• Backpropagation
• Neural Network

Backpropagation(역전파)

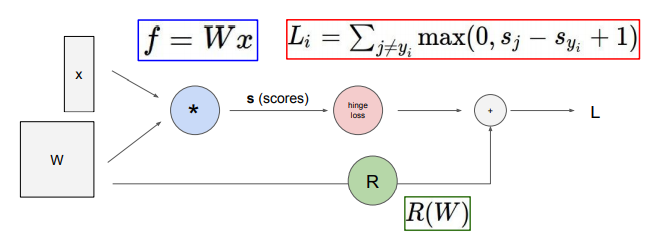
오차를 거슬러 올라가면서 각각의 파라미터에 대한 gradient를 계산하는 과정.
인접한 노드와의 관계를 이용해서 gradient값을 얻을 수 있다.
나는 아래 용어를 다 같은 의미를 지니는 것으로 이해했다.

• x의 gradient
• x에 대해 f를 미분한 값
• 함수 f에서 x에 대한 도함수 값
• df/dx
• x가 함수 f에 미치는 영향

동작 방법:

local gradient를 구하고 chain rule을 이용하여 재귀적으로 upstream gradient를 구한다.

• local gradient: 현재 노드의 기울기
• upstream gradient: 현재 노드로부터 이전 노드로 향하는 기울기

chain rule이란?

역전파에서 gradient를 얻기 위해서 사용된다.
두 함수를 합성한 합성 함수의 도함수에 관한 공식.

y = f(x)와 함수 z = g(y)를 합성한 함수의 미분법은 다음과 같다.

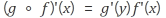
• 역전파 원리로 gradient 구하기. 예제1
  

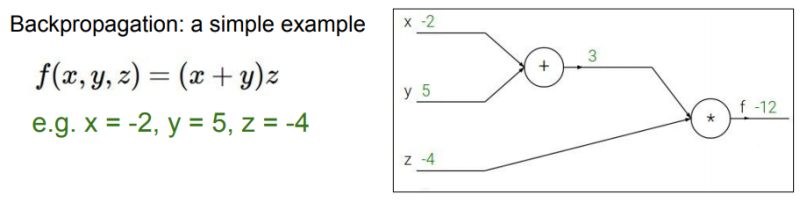
위 수식과 computational graph를 보고 x,y,z의 gradient값을 구하라

원리에 대한 풀이. chain rule을 이용

답

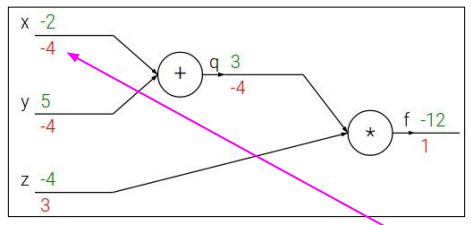
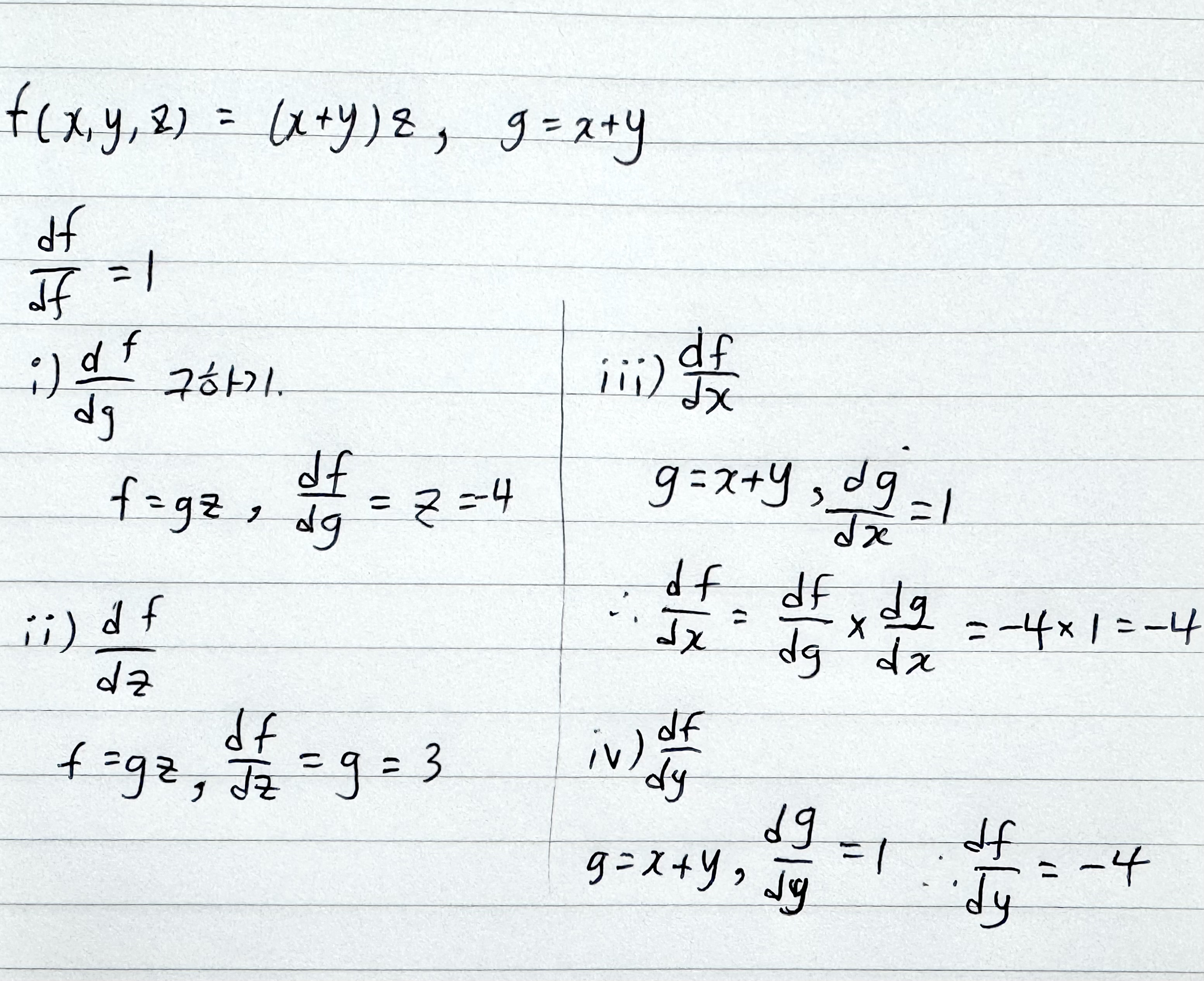
1. 주어진 함수:
   $f(x, y, z) = (x + y)z, \quad g = x + y$

2. 미분 조건:
   $\frac{df}{df} = 1$

3. 문제 풀이:

   
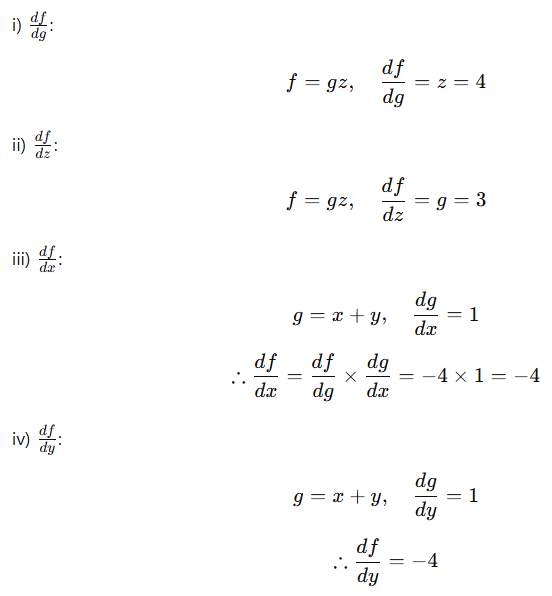
   node의 연산이 x(곱하기)인 경우, gradient = 곱해지는 상대(?) 변수의 계수
   node의 연산이 +인 경우, gradient = (함수의 gradient) * (해당 변수의 계수)

역전파 원리로 gradient 구하기. 예제2(sigmoid 응용)

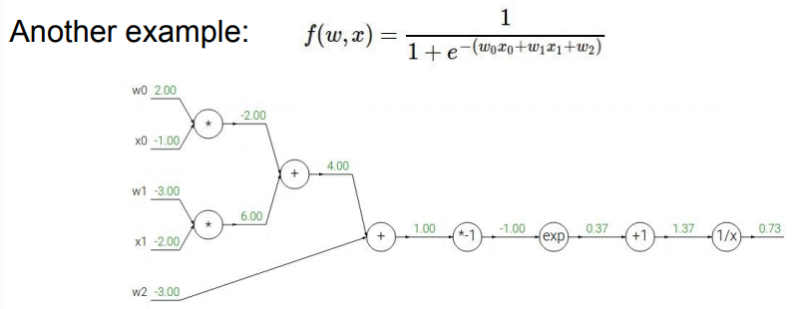
풀이는 이 블로그의 필기 자료로 이해했다.

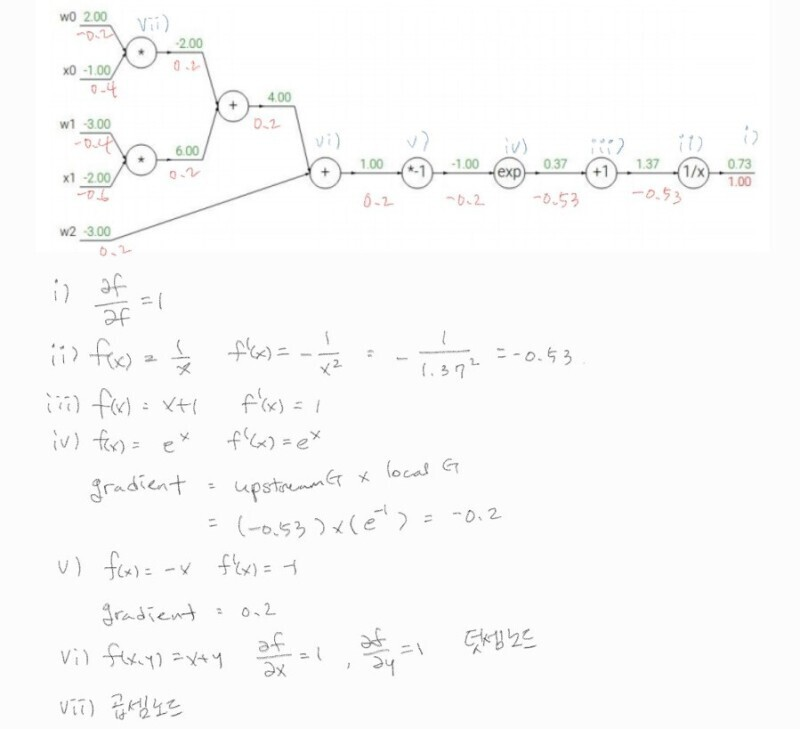
답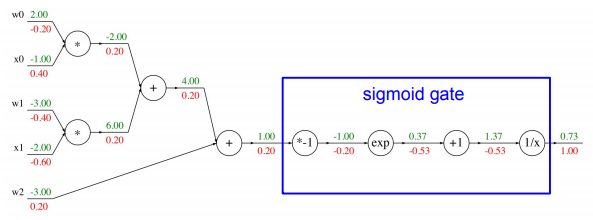

각 연산 단위인 node들을 하나로 묶어 그룹화 할 수 있다.
파란색 ‘sigmoid gate’ 상자 연산은 sigmoid fuction 연산과 동일하다. backpropagation을 수행할 때 우리는 해당 node의 local gradient값만 알면 되기 때문에 sigmoid fuction의 도함수 값만 알면 그림처럼 하나로 그룹화해도 정상적인 backpropagation을 수행할 수 있다.

예시3. 만약 input이 x,y,z가 아니라 벡터라면?

• 이 경우의 gradient는 Jacobian 행렬이 된다. (계산식은 이해 안 됨)

jacobian matrix (자코비안 또는 야코비 행렬)

• 다변수 벡터 함수의 모든 편미분을 모아놓은 행렬
• 비선형 변환을 선형 변환으로 근사시킨 것

풀이

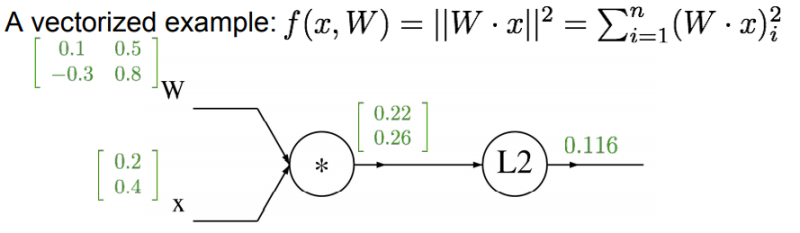
출처: 공대생 노트 창고

감사합니다.. 덕분에 이해했습니다.

답

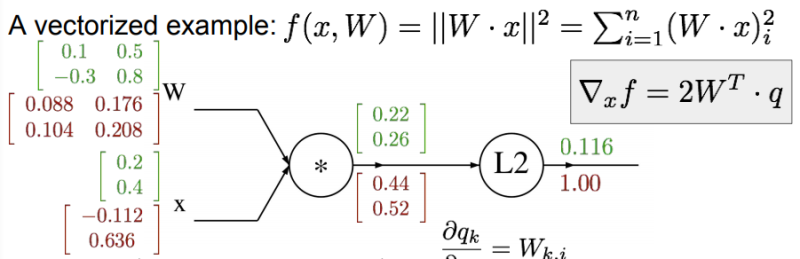
야코비 행렬의 각 행은 입력에 대한 출력의 편미분이 된다.

심화: 자코비안 행렬 이해하기

Neural Network (신경망)

방금까지는 layer가 하나인 lienar function만을 예시로 들었다.
이런 layer를 여러겹 쌓을 수 있다.

선형 레이어 쌓고 그 사이에 비선형 레이어를 추가.

다음 강의에서 배우게 될 활성화 함수

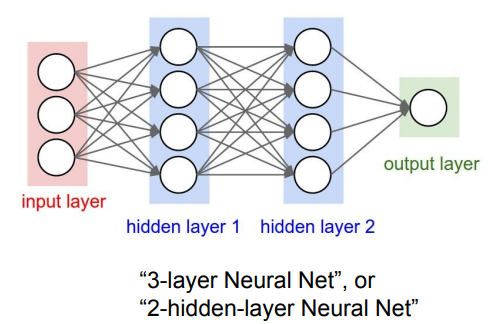
참고:
https://oculus.tistory.com/9
https://velog.io/@cha-suyeon/CS231n-4%EA%B0%95-%EC%A0%95%EB%A6%AC-Introduction-to-Neural-Networks#another-example

---

aside: 딥러닝 프레임워크 라이브러리 Caffe
https://github.com/BVLC/caffe