
목차
- 활성화 함수
- 데이터 전처리
- 모니터링, 파라미터 조절
활성화 함수
활성화 함수가 사용되는 곳
Neural Network의 동작
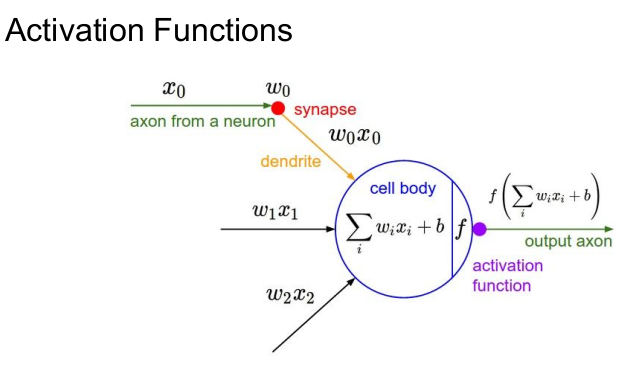
각 뉴런에서 전달된 입력값(xi)이 wi와 곱한 것을 모두 합하고 편향(bias, b)를 더한다. (5단원에서 FC/CNN을 거치는 과정임. 그리고 이 함수는 선형 함수다.) 비선형 함수인 활성화 함수와 연산하여 다음 뉴런으로 나간다.
활성화 함수를 사용하는 이유
- 신경망은 단순한 선형 함수여서 복잡한 패턴을 이해하기에는 무리가 있다. 따라서 비선형인 활성화 함수를 사용해서 더욱 복잡한 비선형 패턴을 더욱 잘 모델링하고 학습할 수 있게 된다.
활성화 함수 종류
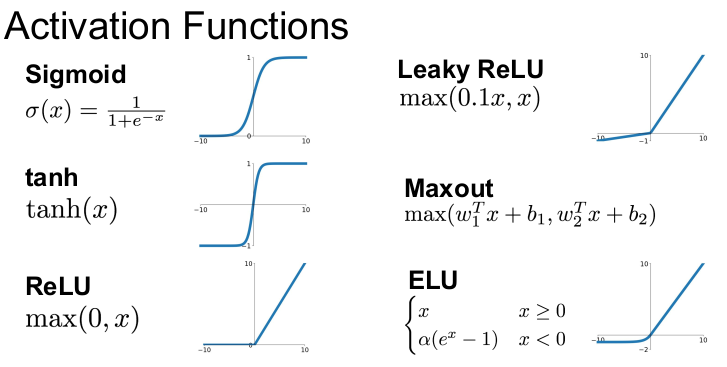
Sigmoid
뉴런의 firing rate를 saturation시키기 때문에 역사적으로 많이 사용되었다.
- firing rate (발화율): 실제 인간 뇌의 뉴런에서 일정 시간 동안 발화(신호를 보내는) 횟수
- saturation(포화): 출력값이 발산되지 않고 0또는 1사이로 제한된다는 의미.
- 즉 위 말의 뜻은 Sigmoid 함수가, 입력되는 신호의 강도에 따라 신호를 보내거나 보내지 않는 (실제 인간 뇌의) 뉴런의 행동을 모방하고, 그 출력값을 0과 1 사이로 제한한다는 것.
하지만 뉴런 값이 0과 1에 가까우면 vanishing gradient(기울기를 죽이는) 문제가 있음.

결과값이 지그재그로 이동함. = zero-centered하지 않음
exp()의 계산 비용이 비싸다 (계산 오래걸림)
탄젠트
출력값의 범위: [-1, 1]
zero-centered함
뉴런이 포화되었을 때 그래디언트를 죽임.
- 기울기가 포화된다란? 기울기가 매우 크거나 작아서 기울기를 올바르게 전파되지 못하는 현상.
ReLU
양수일 때 뉴런이 포화되지 않아 그래디언트가 죽지 않음
수렴 속도도 빠름.
현재 가장 많이 쓰이는 활성화 함수
not zero-centered
기울기가 음수일 때는 포화되기 때문에 출력이 0이 되어 해당 뉴런이 활성화되지 않는 문제( = dead ReLU)가 발생
- dead relu가 발생하는 경우
- 초기화를 잘못한 경우
- learning rate가 지나치게 높은 경우
leacky ReLU
어느 곳에서도 그래디언트가 죽지 않음.
PReLU
negative space에 기울기가 있음.
backpropagation으로 기울기 α를 결정하므로 Leaky ReLU보다 유연함
ELU
ReLU와 Leaky ReLU의 중간. ReLU의 모든 장점을 가지지만
복잡한 exp()(비싼 연산)을 계산한다.
Maxout "Neuron"
ReLU와 Leaky ReLU를 일반화시킨 활성화 함수
w1Tx+b1,w2Tx+b2의 최대값으로 구하기 때문에 선형적인 지역이 나타나므로 뉴런이 포화되지 않고 그래디언트도 죽지 않음
단점: 뉴런당 파라미터가 2배가 됨.
learning rate를 주의하면서 ReLU를 사용해야 한다.
데이터 전처리
zero-centered data로 만들기
정규화(normalized data)
모든 차원이 동일한 범위 안에 있게 해주어 전부 동등한 기여를 하게 함.
하지만 이미지 분석에서는 정규화는 할 필요가 없이 zero-centered 데이터로만 만들면 된다. 입력 이미지는 각 차원이 이미 특정 범위 안에 들어있기 때문
기울기를 초기화하는 방법
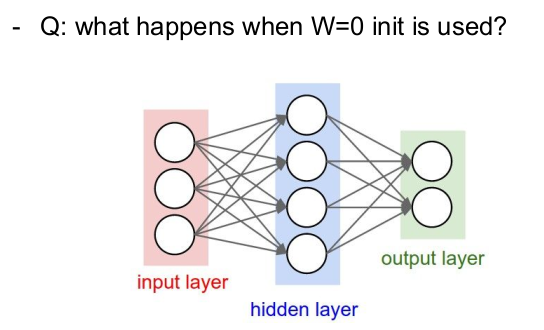
모든 가중치를 0으로 설정하면 모든 뉴런이 같은 일(연산)을 하게 됨. 따라서 출력값은 모두 같고 기울기도 모두 같게 되어 같은 가중치값으로 업데이트된다. (=symmetric breaking이 발생하지 않음.)
우리는 각 뉴런이 다른 가중치 값을 가지길 원함
초기화 방법1: 임의의 작은 값으로 초기화 - batch Normlization(배치 정규화)
gaussian의 범위(정규분포로 변환할때?)로 activation을 유지시키는 또 다른 방법.
미니배치(mini-batch)를 단위로 '입력 데이터'의 평균과 분산을 이용하여 정규화.
출력으로 나온 각 뉴런마다 bn을 적용.
reguralization 효과도 줌.
초기화 방법2: Xavier initialization
가우시안 표준 정규 분포에서 랜덤으로 뽑은 값을 "입력의 수"로 스케일링. 입출력의 분산을 맞춤
기울기 소실
입력에 대한 출력의 변화가 일정 범위에서 거의 일어나지 않는 현상.
모니터링, 하이퍼파라미터 조정
데이터 전처리 zero-mean
하이퍼파라미터 조정: cross-validation, grid search
