3.1 - Floating Point Number

1. Floating Point

• Scientific notations

  • 소수점 기준 왼쪽에는 숫자 하나만 존재
    -> Normalized : 왼쪽 숫자는 1 ~ 9
    

• Floating number 라고 불리는 이유 : 소수를 표현하는 방법은 다양하다.
  -> 소수점의 위치를 움직이면서 같은 소수를 다양하게 표현할 수 있다.
  ex) 2.7 = 27 x 10^-2, 270 x 10^-3 등

• Two representations by IEEE Standard 754
  : 정확도의 차이

  1. Single precision : 1-bit sign, 8-bit exponent, 23-bit fraction
  2. Double precision : 1-bit sign, 11-bit exponent, 52-bit fraction
     

2. Floating Point Representation In Binary

• Fraction and Exponent

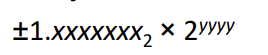
• Single precision representation
  

  • Sign : 부호를 결정
    -> 1 : 음수, 0 : 양수
  • Exponent : 표현할 수 있는 숫자의 크기 결정
    -> 8 bit : -128 ~ 127
    -> Range in decimal : 2.0 x 10^-38 ~ 2.0 x 10^38
  • Fraction : 얼마나 정밀하게 표현할 수 있는지를 결정
    -> fraction ↑, 정밀도 ↑

• Double precision representation
  

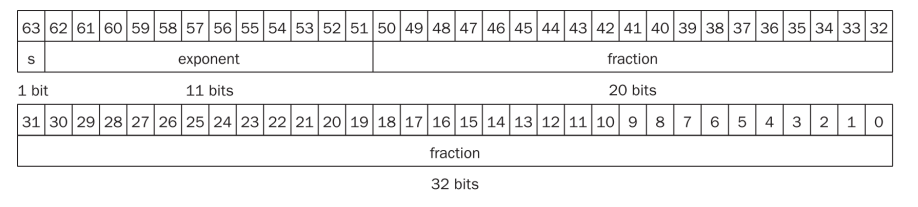
  • Sign : 부호를 결정
  • Exponent : 표현할 수 있는 숫자의 크기 결정
    -> 11 bit : -1024 ~ 1023
    -> Range in decimal : 2.0 x 10^-308 ~ 2.0 x 10^308
  • Fraction : 얼마나 정밀하게 표현할 수 있는지를 결정

• Biased notation

  • 2의 보수를 사용하기 때문에 시각적으로 X가 더 커보인다. (sorting 어려움)
    
    
    
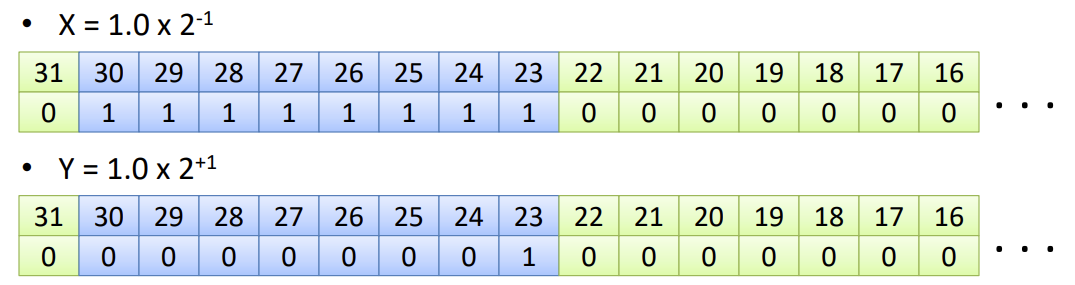
  • Rearranging the exponent value range : Sorting을 효율적으로 하기 위해서 bias 값을 더해서 표현한다.
    -> Bias : 2^(k-1) - 1, where k is the length of the exponent
    
    
    
  • IEEE uses a bias of 127 for single precision, 1023 for double precision
    -> 표현 될 때는 Exponent + Bias
    -> 해석 할 때는 Exponent - Bias
    
    
    
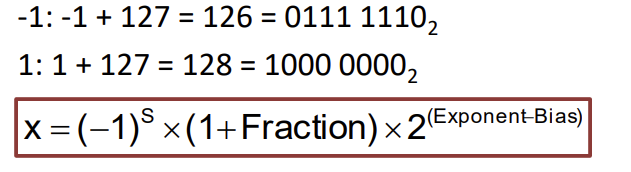
  • Example : 8 bit로 exponent를 사용할 때 표현할 수 있는 범위는 -128 ~ 127
    
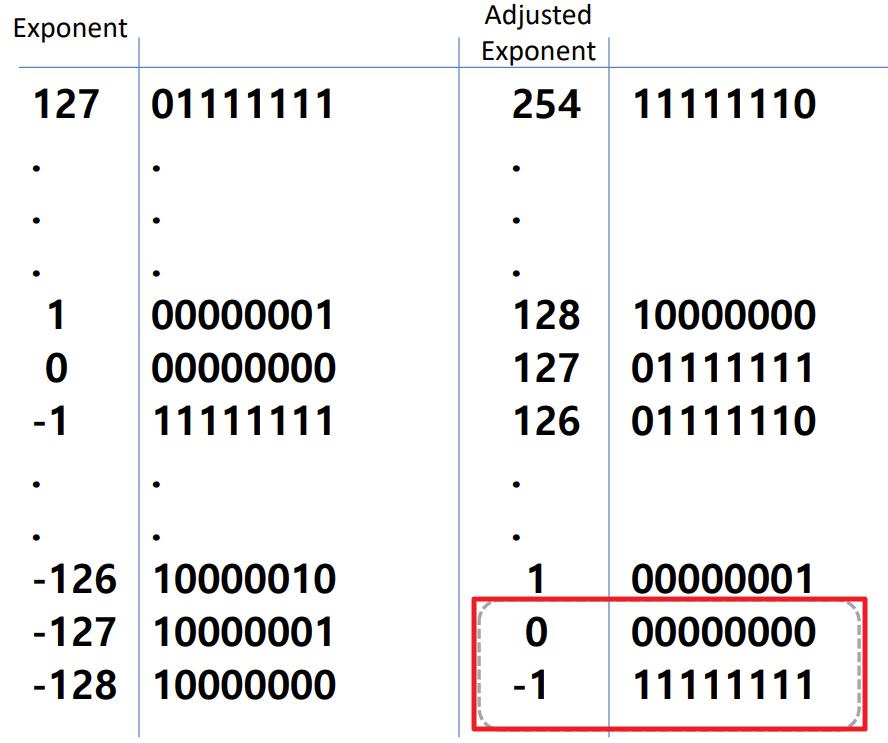
    • 왼쪽과 같이 표현하면 sorting하고 직관적으로 판단하기 어려움
    • 오른쪽과 같이 bias (127)를 더함으로써 각 bit가 위치한 곳만 보고 판단, sorting에 용이하다.
    • Exponent : 00000000, Fraction 0 -> 0 (reserved)
    • Exponent : 11111111(255), Fraction 0 -> Infinity (reserved)
    • Exponent : 11111111(255), Fraction Nonzero -> NaN

• Example

  1. Represent below
     
  2. Represent -0.75
  3. Represent 968.75
     -> 0 10000010 00110110000000000000000
  4. What number does this represent?
     

• Density of Floating Point Numbers
  : In 32 bits, the maximum number of different values that can be represented is 2^32
  -> Larger numbers are spaced more sparsely than smaller numbers