개요

본 블로그 포스팅은 수도권 ICT 이노베이션 스퀘어에서 진행하는 인공지능 고급-시각 강의의 CNN알고리즘 강좌 내용을 필자가 다시 복기한 내용에 관한 것입니다.

---

1. 선형회귀모델

회귀모델, 혹은 회귀분석 등 데이터 분석에 사용되는 머신러닝 도구를 학습하고자 하는데
말이 어렵다.
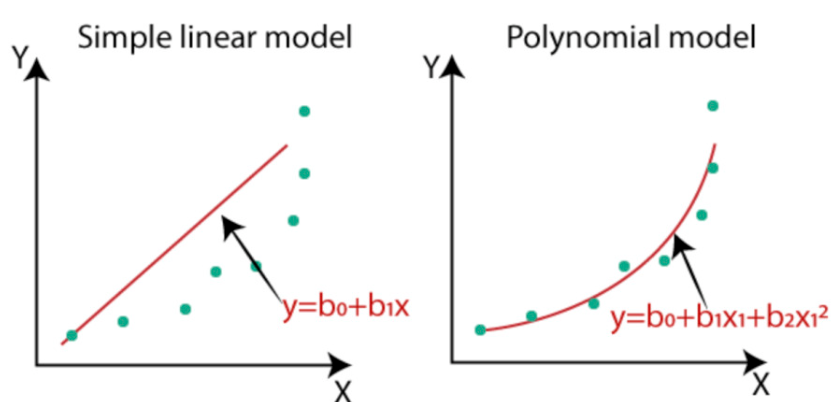위 그림처럼 어떤 데이터를 수집했을 때 그것에 따른 추세선을 그리는 작업을 회귀분석이라 보면 되고 이 추세선이 회귀모델에 속한다 보면 된다.

그러면 코드로 실습을 해보자

import torch
import torch.nn as nn
import torch.optim as optim

# 데이터 정의
x = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=torch.float32)
y = torch.tensor([3, 5, 5, 6, 7, 7, 8, 9, 9, 10], dtype=torch.float32)
# requires_grad=False로 선언된 값들이니 '상수'에 속한다 보면 된다. -> 따라서 변하지 않는 값

# 가중치와 편향 정의
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)
# 값이 변하는 변수에 속하며, 초기값은 랜덤으로 준다. -> 그리고 그 랜덤의 사이즈는 1차원 스칼라값이다.
# size = [1]

# 손실 함수 정의 -> 이게 Loss_func이다.
def compute_loss():
    y_pred = w * x + b
    loss = torch.mean((y - y_pred) ** 2) #오차는 음수가 나오면 힘드니 제곱해서 오직 양수로만
    return loss
    
# 학습 루프
for i in range(1000):
    optimizer.zero_grad()  # 옵티마이저의 변화도를 0으로 설정
    loss = compute_loss()  # 손실 값 계산
    loss.backward()        # 손실에 대한 역전파 계산
    optimizer.step()       # 가중치 업데이트

    if i % 100 == 0:
        print(f"{i}, loss: {loss.item()}")

print(f"final w: {w.item():.3f}")
print(f"final b: {b.item():.3f}")

전체 코드를 먼저 붙이고 코드리뷰를 하겟다.

1) 코드리뷰

x = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=torch.float32)
y = torch.tensor([3, 5, 5, 6, 7, 7, 8, 9, 9, 10], dtype=torch.float32)

여기서 x는 첫번재 그래프에서 x축을 그리려고 만든 데이터이고
y는 이 x가 시간(t)라 가정한다면, 시간마다 측정된 데이터 라 보면 된다.

이렇게 수식화 할 수 있으며, 여기서 y는 종속변수, x는 독립변수가 된다.

그리고 Tensor 자료형으로 치면 이 y랑 x는 전체 회귀모델을 세우고 예측을 하는 일련의 과정 동안 변동이 발생하면 안되는 값이니
(변동을 한다는 것은 중간에 수집한 데이터를 바꾸는 작업에 속하니) requires_grad=False 옵션으로 선언되었다 보면 된다.

# 가중치와 편향 정의
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

다음으로 w,b를 선언하였는데 이게 아래의 수식으로 모델링 된다 보면 된다.

여기서 w가 weight, b가 bias라고 표현하는데 아무튼 이 수식이

def compute_loss():
    y_pred = w * x + b
    loss = torch.mean((y - y_pred) ** 2) #오차는 음수가 나오면 힘드니 제곱해서 오직 양수로만
    return loss

이 함수구문에서 y_pred = w * x +b로 표현된다 보면 된다.

그럼 내가 임의로 추세선을 그려서 얻은 y값과
실제 y값은 차이가 나기 마련이다.

이것을 표현하기 위한 문자로 $\hat{y}$y_pred, $y$y를 설정했을 때

라는 수식을 만들 수 있다 이 $e$error을 0에 가깝게 하는 것이 목적이고
error을 전체 $y$데이터에랑 수식으로 얻은 $\hat{y}$에서 모두 더한값을 0으로 만들어야 하니
error을 구할 때 어떤 n번째 $y$, $\hat{y}$는 양수가 나올 수 도 있고, 어떤 k번재 $y$, $\hat{y}$는 음수가 나올 수도 있으니

깔끔하게 모든 error(n)에 대하여 제곱을 하고 더하는 식을 쓰는 식으로 Loss Function을 설계하는 것이다.

이 과정 Least Square Estimation이라 부르며, 이걸 다 포함한것이 def compute_loss():코드로 구현된 것이다.

# 옵티마이저 정의
optimizer = optim.Adam([w, b], lr=0.07)

이 코드는

# 학습 루프
for i in range(1000):
    optimizer.zero_grad()  # 옵티마이저의 변화도를 0으로 설정
    loss = compute_loss()  # 손실 값 계산
    loss.backward()        # 손실에 대한 역전파 계산
    optimizer.step()       # 가중치 업데이트

    if i % 100 == 0:
        print(f"{i}, loss: {loss.item()}")

와 함께 설명하려는데

처음 임의의 w와 b를 설정하고 Loss를 구했다 가정하자.
이 Loss(첫번째)가 0과는 큰 차이가 나는 값이 났으니
다음 w랑 b를 설정하고 다시 구한 Loss(두번째)는 Loss(첫번째) 보다는 개선이 되어야 할 것이다.

이 개선이 되게끔 해주는 함수가
optimizer = optim.Adam([w, b], lr=0.07)라 보면 된다.

이게 최적제어론 - 경사하강법 이거까지 설명해야 하는데 이건 넘어가도록 하겠다.

아무튼 Loss를 계속 0에 가깝게 만들어주는 함수가 저 옵티마이저이란 메서드이고
필요로 하는 인자는 개선을 시켜야 할 대상인 w랑 b, 또다른 인자로 lr(learning rate)는 0.07이란 값을 넣었는데

Loss(첫번째)란 값이 4란 값이 나왔을 때

Loss(두번째)값은 3.93, 즉 4 - lr값이 되게끔 해주는 step이라 이해하고 넘어가면 된다.

이게 경사하강법에서 Global Miniumum을 탐색하기 위한 다음 점의 행보를 결정해주는 값인데.. 아무튼 저 값이 크고 작음에 따라 아래의 그림처럼 최저점 탐색을 한다.. 보면된다.

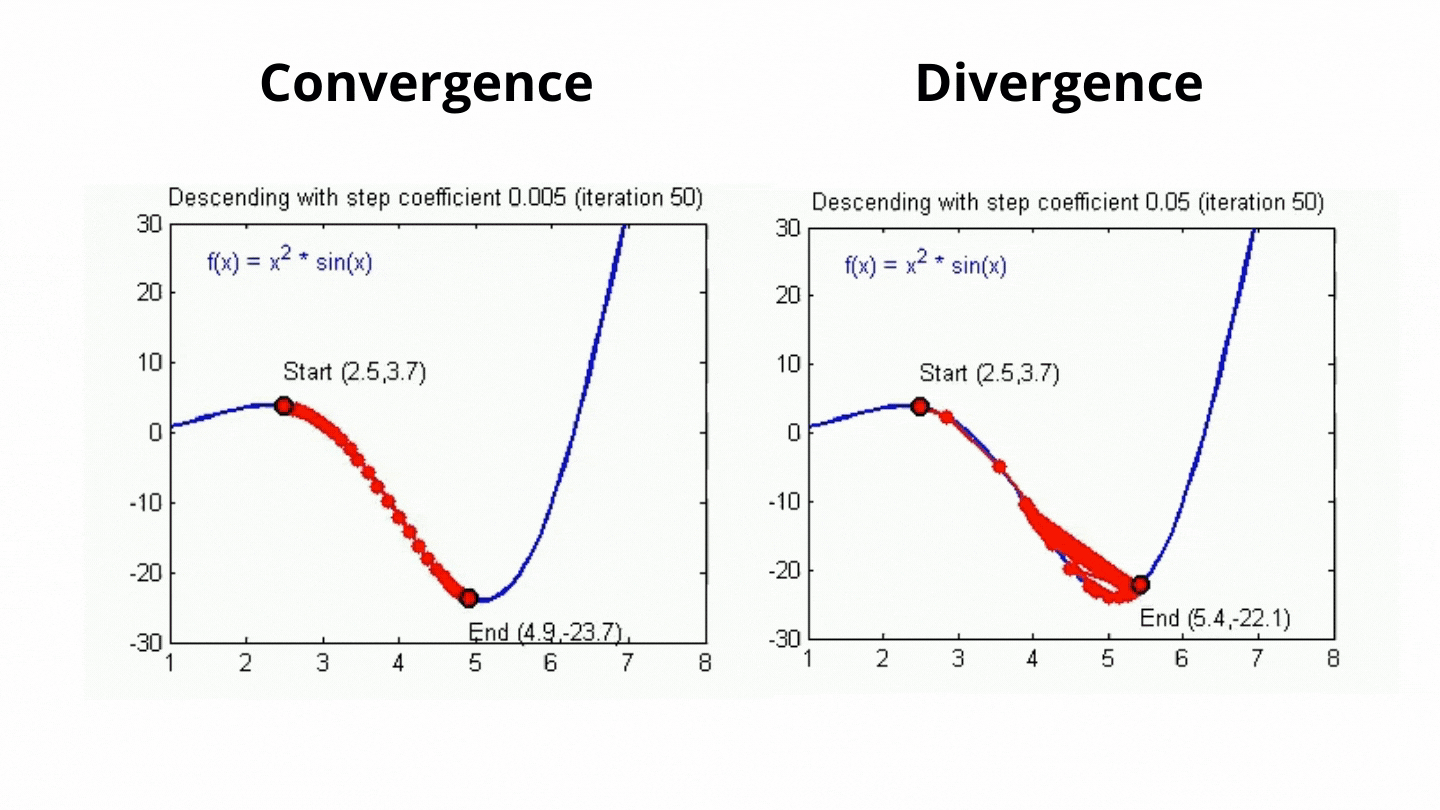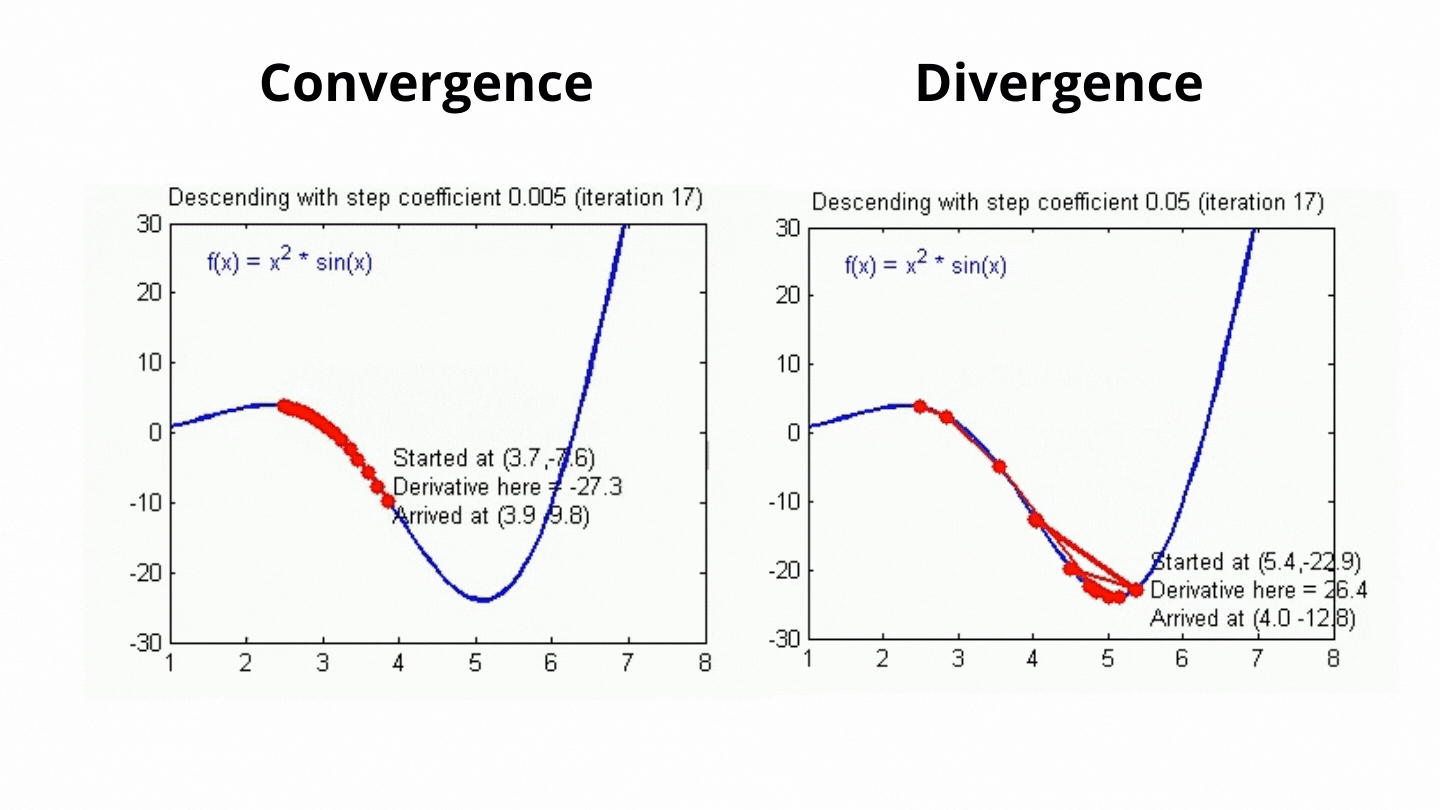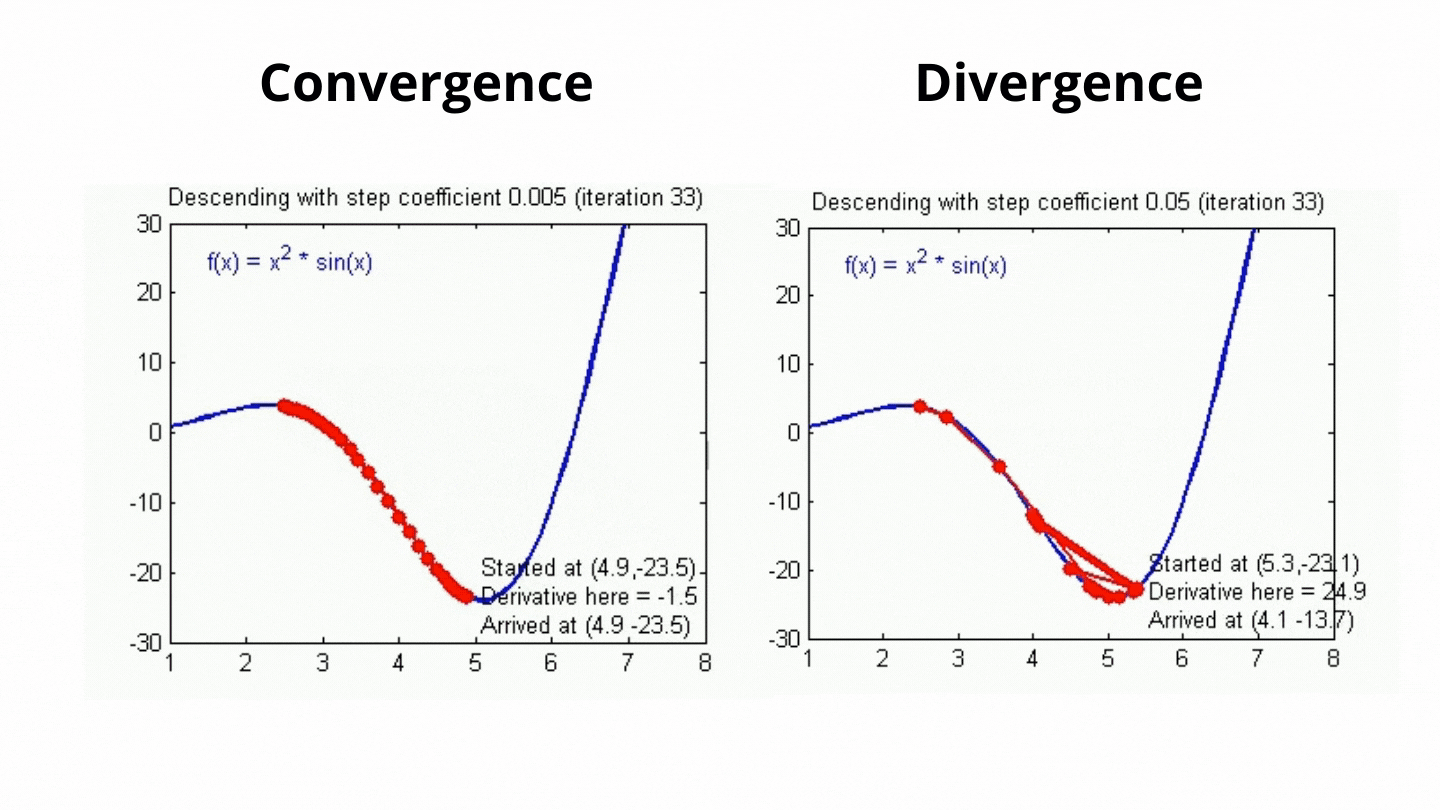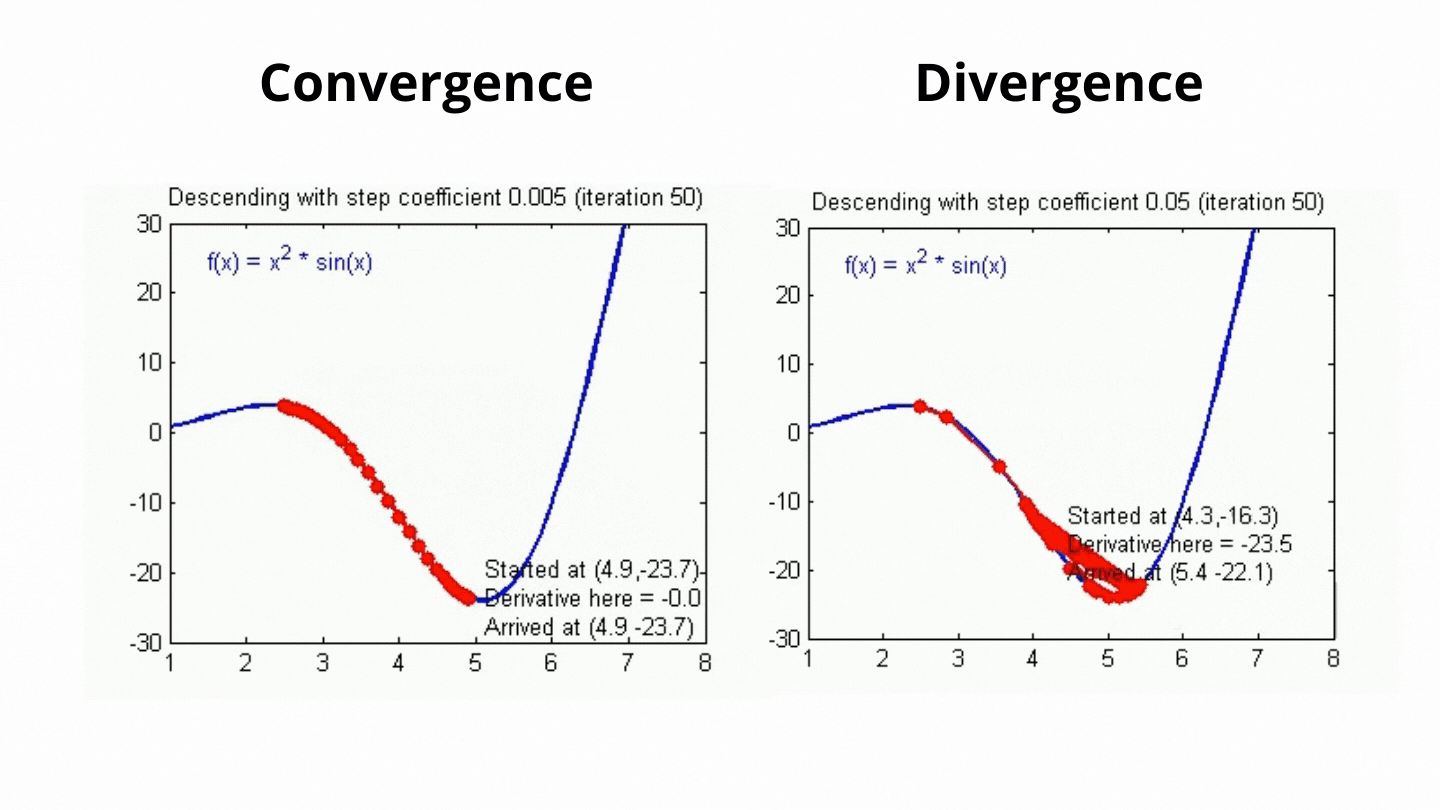
아무튼 위 gif이미지처럼 최저점(loss가 0에 가장 가까운 점)을 찾는 과정이 for i in range(1000):에서 수행된다 보면 된다.

위 코드 리뷰는 이정도로 하고 코드를 실행하면 아래와 같은 결과를 얻을 수 있을 것이다.

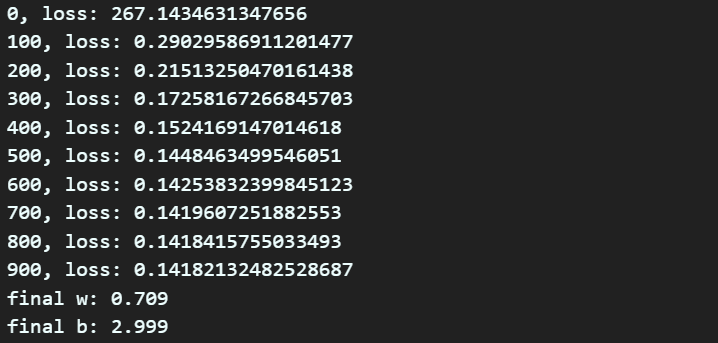
여기서 얻은 w랑 b를 y데이터랑 같이 연관하여 그림을 그리고 싶다면
아래의 코드를 실행하면 된다.

import matplotlib.pyplot as plt


x_np = x.numpy()
y_np = y.numpy()

# 학습된 가중치와 편향으로 예측
y_pred = (w * x + b).detach().numpy()

plt.plot(x_np, y_np, 'bo')  # 실제 데이터
plt.plot(x_np, y_pred, 'red')  # 예측한 데이터
plt.show()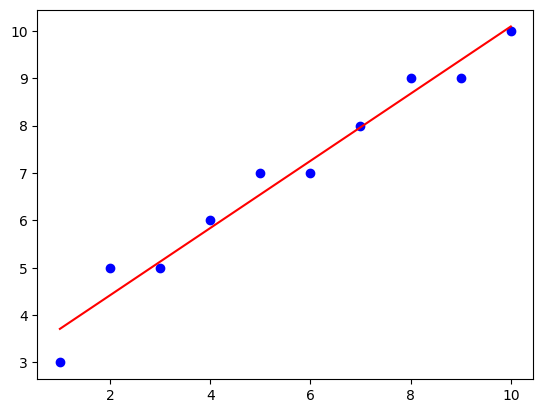

이때 그림을 그리는 y_pred에서

y_pred = (w * x + b).detach().numpy()

.detach() 메서드가 있다.
이 메서드는 Gradient의 역전파를 막는 함수로써
설명이 어려우니 변동되는 값이 될 가능성이 있는 y_pred를 상수로 고정하는 역할이라 보면 된다.

그러니까.. 결과를 출력해야 하는 시점의 데이터는 .detach()메서드를 붙여서 값을 고정시킨다 보면 된다. 그 이후에는 .numpy()메서드로 plot 메서드가 받아들일 수 있는 매트릭스 자료형인 numpy자료형으로 변환시키는 과정이라 보면 된다.

---

2. 신경망 모델

이번에는 신경망, 퍼셉트론 형식으로 비선형 회귀모델을 세워서 추세선을 그려보자

흔히 딥러닝 하면 보이는
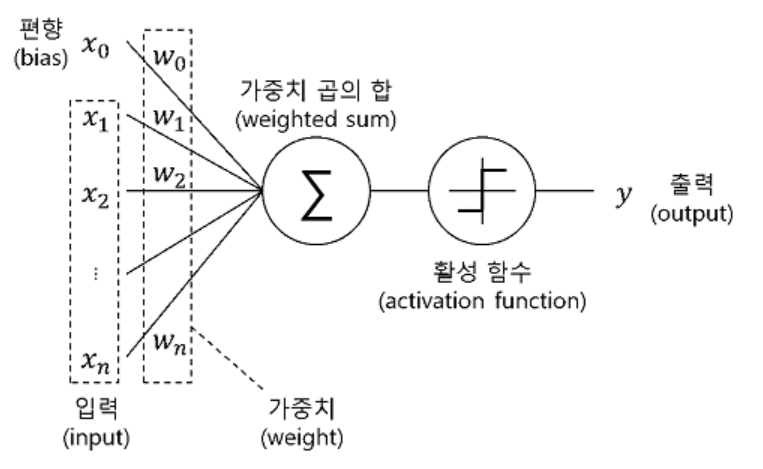위 그림을 코드로 구현해보자는 뜻이다.

import torch
import torch.nn as nn
import torch.optim as optim
from torchsummary import summary

# 데이터 생성
x = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=torch.float32).view(-1, 1)
y = torch.tensor([3, 5, 5, 6, 7, 7, 8, 9, 9, 10], dtype=torch.float32).view(-1, 1)

class SimpleModel2(nn.Module):
    def __init__(self):
        super(SimpleModel2, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(1, 10),
            nn.Tanh(),
            nn.Linear(10, 1)
        )
    
    def forward(self, x):
        # x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

model2 = SimpleModel2()

summary(model2, input_size=(1, ), device='cpu')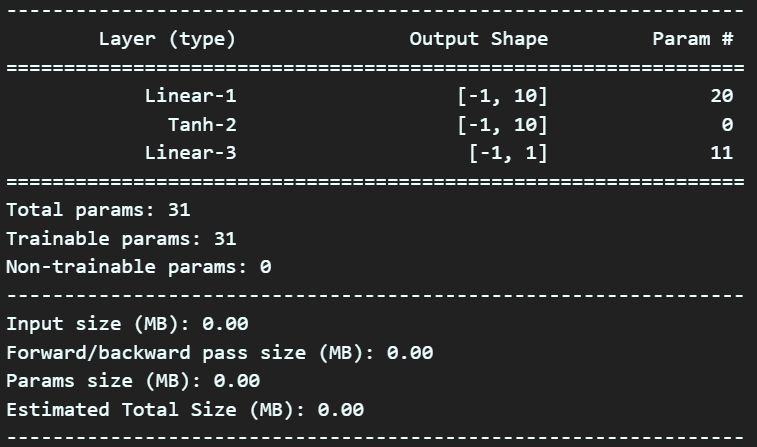

# 손실 함수 및 옵티마이저 정의
criterion = nn.MSELoss()
optimizer = optim.Adam(model2.parameters(), lr=0.01)

epochs = 1000
for epoch in range(epochs):
    model2.train()
    optimizer.zero_grad()
    
    outputs = model2(x)
    loss = criterion(outputs, y)
    
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')

# 예측
model2.eval()
with torch.no_grad():
    predicted = model2(x)
    print(predicted)

코드에 대한 설명을 하자면 아래와 같다.

# 데이터 생성
x = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=torch.float32).view(-1, 1)
y = torch.tensor([3, 5, 5, 6, 7, 7, 8, 9, 9, 10], dtype=torch.float32).view(-1, 1)

여기서 마지막에 .view(-1, 1)메서드가 붙었는데
이 메서드는 차원변환을 해주는 .reshape함수랑 동일한 기능을 한다 보면 되지만 메모리 절약 차원에서 view함수를 텐서 자료형의 차원변환에 더 많이 사용한다.

참고로 x와 y의 원본 데이터가 1차원(10)이기에 이를 2차원(10,1)로 만들어 준다 보면 된다.

일단 기본적으로 신경망에 입력할 때는 2차원 데이터로 입력시켜야 한다.

그러면 x 데이터가 아래와 같이 흔히 행렬에서 transpose(전치행렬 처럼 변한다

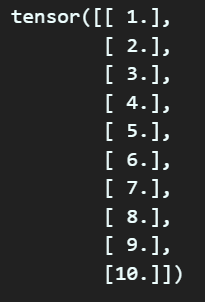
이 다음에 설계한 인공신경망에 x데이터를 통과시켜서 각각의 예측값 $\hat{y}$y_pred를 얻는것인데 이것에 대한 동작 클래스는 아래와 같다.

class SimpleModel2(nn.Module):
    def __init__(self):
        super(SimpleModel2, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(1, 10),
            nn.Tanh(),
            nn.Linear(10, 1)
        )
    
    def forward(self, x):
        # x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

여기서 nn.Sequential은 층으로 쌓으라는 코드이고
nn.Linear -> nn.Tanh -> nn.Linear 3개의 층을 차례로 넘어가라는 식이라 보면 된다.

여기서 사용되는
nn.Linear은 파이토치에서 제공하는 선형 변환 레이어로 인자는 2개를 필수로 필요하는데
각각 (in_features, out_features)이다.
1번 층 nn.Linear는 입력 텐서의 크기가 1인 것을 10으로 선형 변환을 하라는 뜻이며
x 데이터가 (10x1)이니 1번 층을 통과하면 10x10의 메트릭스가 된다.

이를 다시 Tanh 활성화 함수를 거쳐서 비선형성을 만들고 다시 10x10 Feature을 텐서 크기를 1로 축소시키는 2번 층을 거쳐서 (10x1) 차원의 $\hat{y}$y_pred이 만들어진다.. 이렇게 보면 된다.

$\hat{y}$y_pred과 $y$간의 오차를 구하는 Loss Function과 이 Loss를 GM으로 수렴시키는 수렴 방법론에 해당하는 옵티마이저는

# 손실 함수 및 옵티마이저 정의
criterion = nn.MSELoss()
optimizer = optim.Adam(model2.parameters(), lr=0.01)

에 나와있는 설정을 따르며, 이것에 대한 설명은 넘어가도록 하겠다...

그리고 모델의 훈련 for epoch in range(epochs):

그리고 훈련된 모델의 최종 예측 with torch.no_grad():

을 수행하여 최종 Loss 값에 해당하는 y_pred를 구하게 된다.

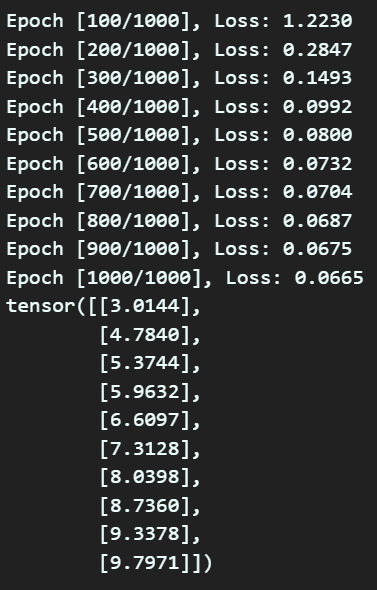
위 과정을 역시 그림으로 그리면 아래의 코드를 사용하면 된다

import numpy as np
import matplotlib.pyplot as plt

# 시각화
x_np = x.numpy()
y_np = y.numpy()
predicted_np = predicted.numpy()

plt.plot(x_np, y_np, 'bo', label='Original data')
plt.plot(x_np, predicted_np, 'r', label='Fitted line')
plt.legend()
plt.show()