개요
본 블로그 포스팅은 수도권 ICT 이노베이션 스퀘어에서 진행하는 인공지능 고급-시각 강의의 CNN알고리즘 강좌 내용을 필자가 다시 복기한 내용에 관한 것입니다.
0. Tensor - Numpy
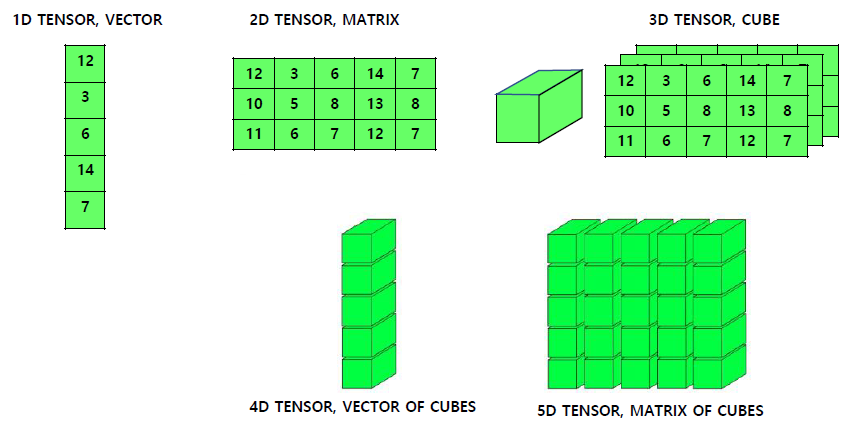강의에서 Tensor 자료형과 이를 다루기 위한 Numpy자료형의 변환, 그리고 Numpy자료형으로 전환시 이점과 사용 가능한 메서드에 대한 강의가 진행되었으나, 짧게 설명하고 넘어가겠다.
n1 = np.arange(24).reshape(3,-1)np.reshape메서드에서 마지막 -1 항목의 경우 자동계산에 속하는 것으로, [3x?]배열로 마지막 ?는 알아서 채우라는 뜻이다.
현재 코드로는 n1은 np.arange로 1차원 리스트에 원소가 24개이니 자동으로 [3x8]행렬로 재배치된다.
# 1차원 텐서 생성
a = torch.arange(6)
print("원래 텐서:\n", a)
# 2차원 텐서로 변경
view_tensor = a.view(2, 3)참고로 np.array보다는 Tensor 자료형에서 직접 모양 변환을 더 많이 사용하며, 이때 torch.view() 메서드를 사용한다.
n3 = np.arrange(24).reshape(2,-1, 4)
n4 = np.transpose(n3, (1,2,0))2차원 이상의 np.array형태 자료형은 axis번호로 차원의 축을 관리하는데, 0, 1, 2,,, 이런식으로 번호를 매긴다.
이 축의 순서를 교체하는 메서드가 np.transpose이다.
x1 = np.array([0, 1, 2])
x1_1 = np.expand_dims(x1, axis=0)np.exepnd_dims은 np.array 자료형의 차원 확장하는데 사용되는 메서드이나
차원의 확장, 축소는 Tensor자료형을 numpy 자료형으로 변환해서 작업하기 보다는
Tensor자료형에서 torch.squeeze, torch.unsqueeze메서드를 활용해 다이렉트로 차원관리하는 경우가 더 많다.
tensor_1 = torch.tensor([[[1, 2, 3]], [[4, 5, 6]]])
#0번째 차원 제거
tnesor_2 = tensor_1.squeeze(0)
#0번째 차원 추가
tensor_3 = tensor_1.unsqueeze(0)다음으로 행렬을 연결하는데 사용되는 np.stack메서드이다.
# 두 개의 2차원 배열 생성
a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[7, 8, 9], [10, 11, 12]])
# 새로운 축(axis=0)을 따라 배열 쌓기
stacked_array = np.stack((a, b), axis=0)
print(stacked_array)
print("shape:", stacked_array.shape)
# 새로운 축(axis=1)을 따라 배열 쌓기
stacked_array = np.stack((a, b), axis=1)
print(stacked_array)
print("shape:", stacked_array.shape)
# 새로운 축(axis=2)을 따라 배열 쌓기
stacked_array = np.stack((a, b), axis=2)
print(stacked_array)
print("shape:", stacked_array.shape)이 또한 Tensor자료형을 연결(concatenate)하는 메서드인 torch.cat을 더 많이 사용한다.
# 2차원 텐서 생성
t1 = torch.tensor([[1, 2], [3, 4]])
t2 = torch.tensor([[5, 6], [7, 8]])
# 0번째 차원을 따라 연결 (행을 기준으로 연결)
result_dim0 = torch.cat((t1, t2), dim=0)
print("0번째 차원을 따라 연결 결과:\n", result_dim0)
# 1번째 차원을 따라 연결 (열을 기준으로 연결)
result_dim1 = torch.cat((t1, t2), dim=1)
print("1번째 차원을 따라 연결 결과:\n", result_dim1)1. 합성곱 연산
입력 데이터에 대하여 필터(커널)을 적용해 새로운 합성곱 결과물을 결과를 만들어 내는 것이 Convolution Neural Network(CNN)의 기본이라 볼 수 있다.
이 CNN은 시각 데이터 처리에 효과적이고, 합성곱 연산을 통해서 입력 데이터의 중요한 특징을 자동으로 추출, 이 추출된 특징을 여러 층(Layer)으로 전달하여,
시각 데이터 처리의 목표인 분류, 탐지, 세분화 등의 작업에 활용한다.
이 합성곱 연산은 아래의 이미지처럼 커널이 입력 이미지(Map) 위를 움직이며 픽셀별로 원소곱을 한 뒤 이 결과값을 모두 더하는 과정이라 볼 수 있다.
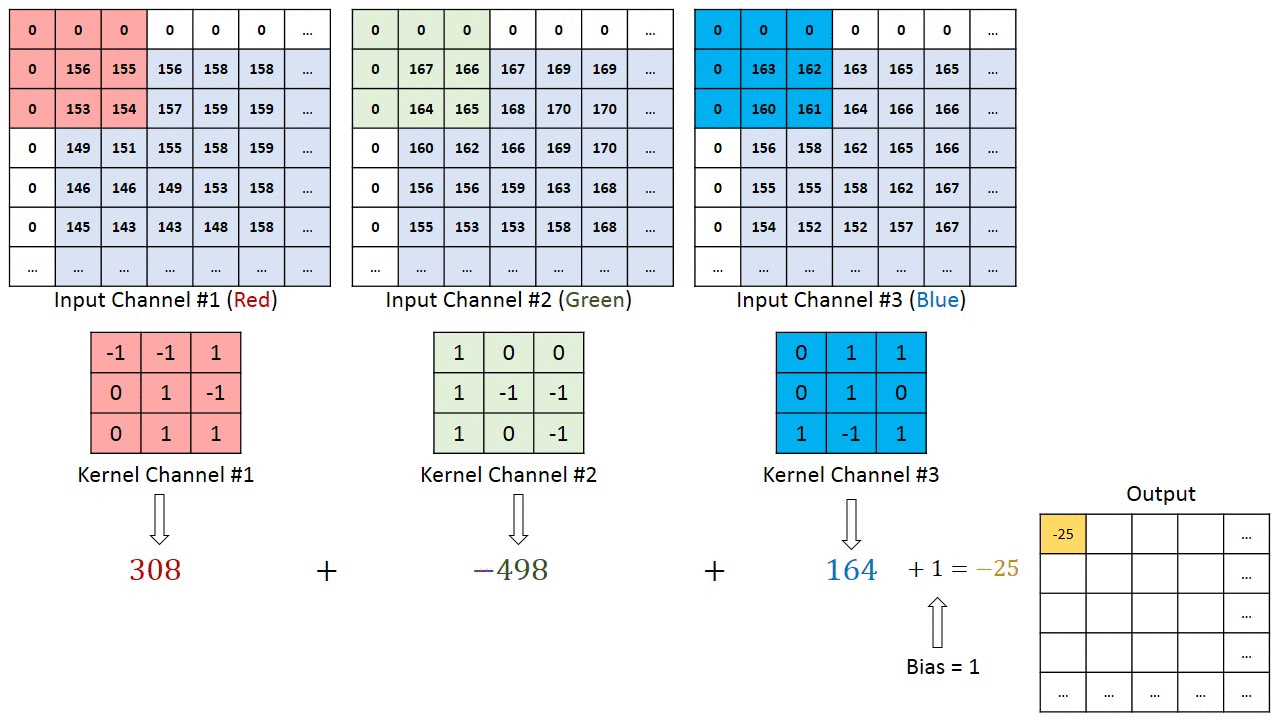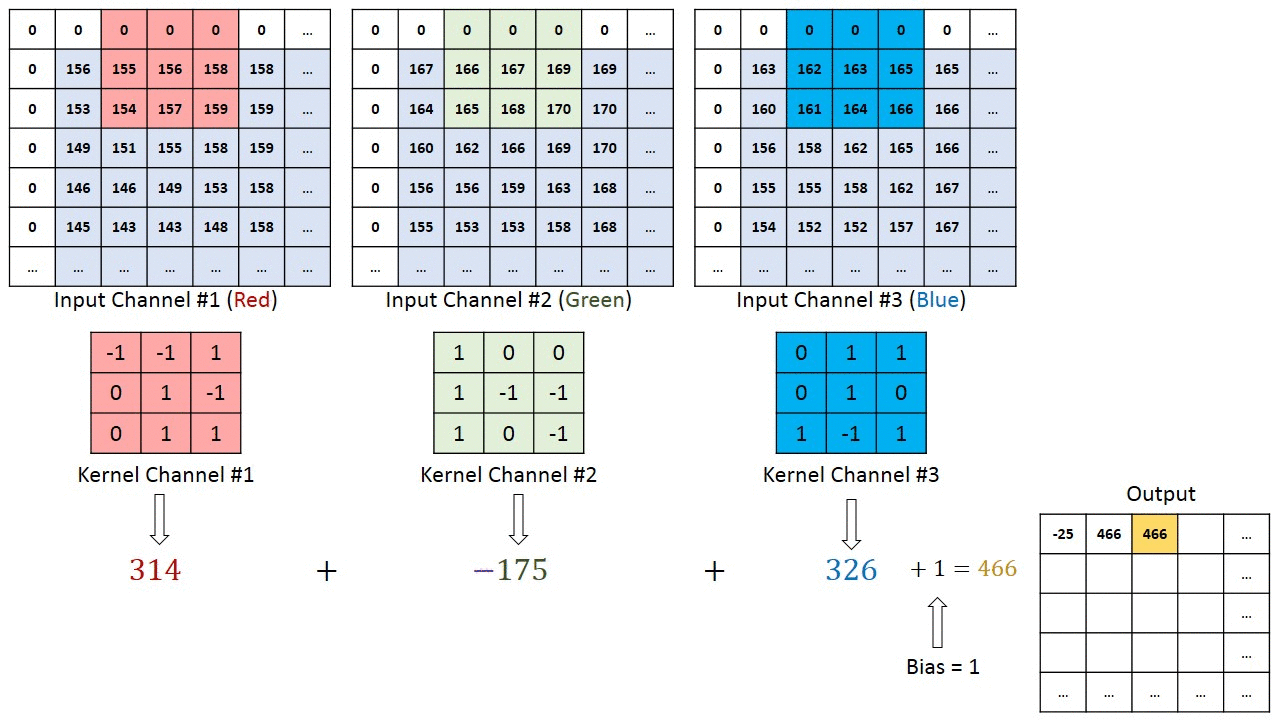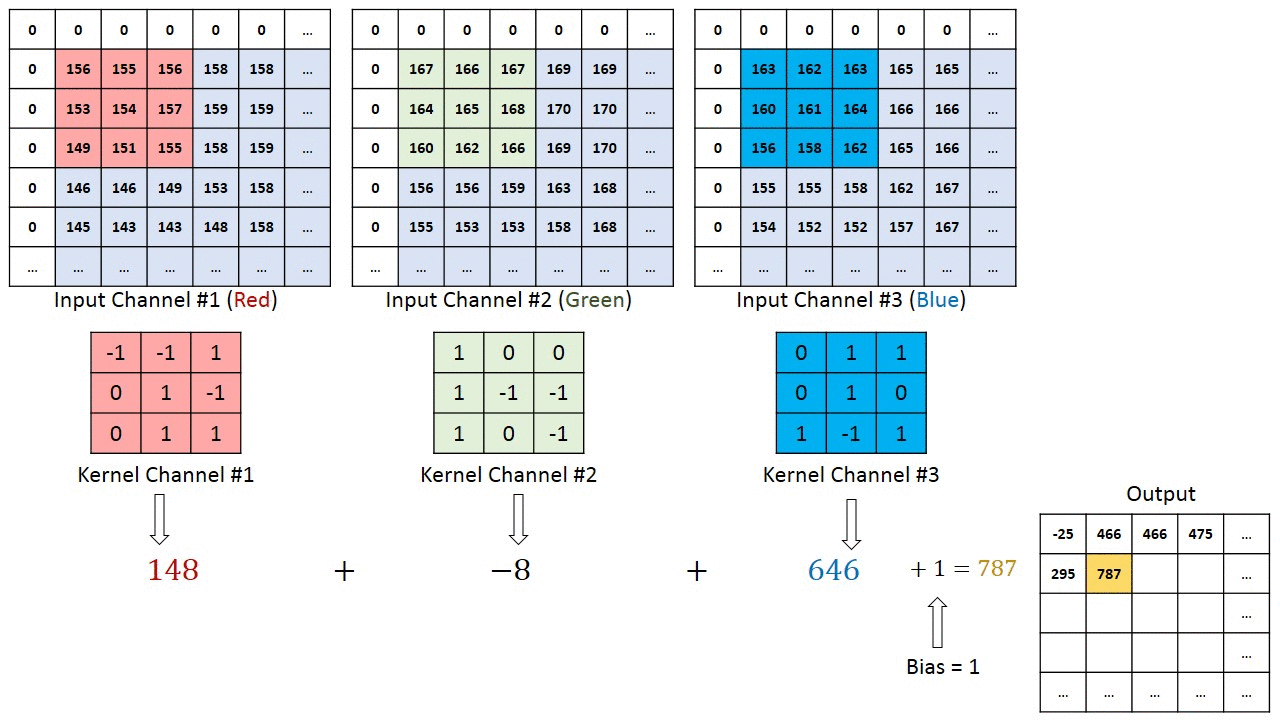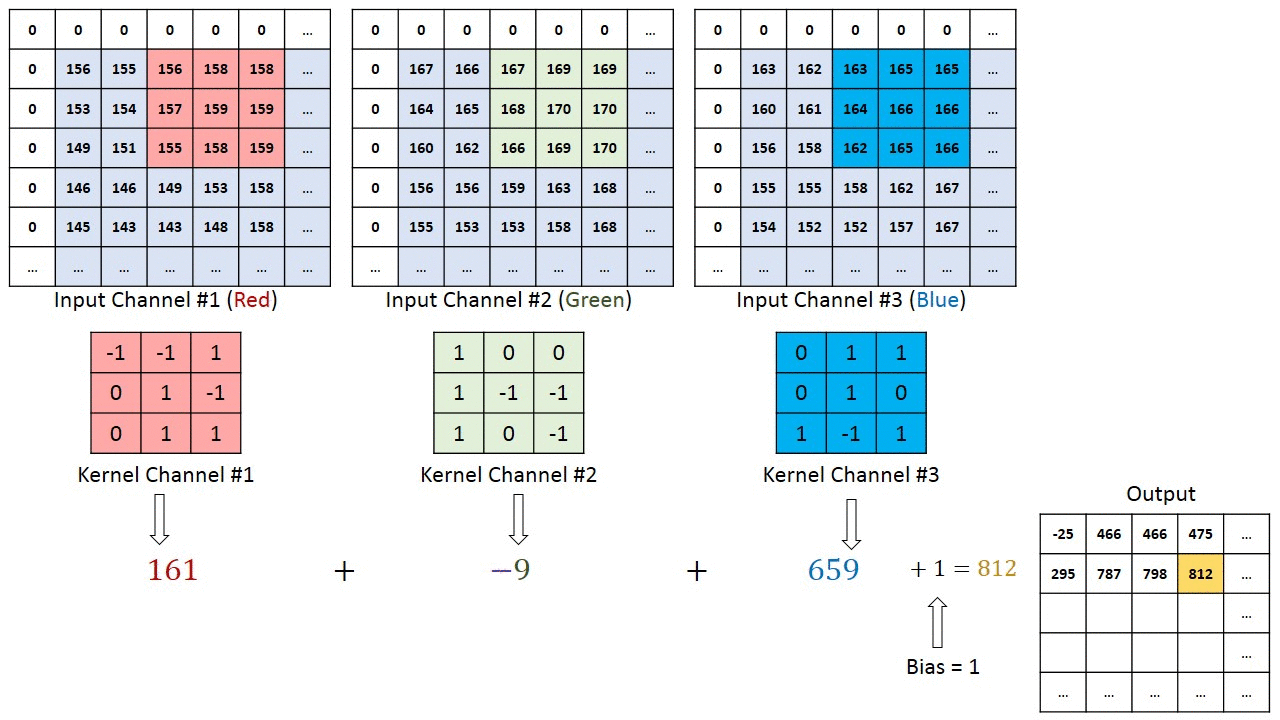이 합성곱을 사용하면 중요한 정보를 유지하면서, 노이즈를 줄일 수 있는 장점이 있는데
이것에 대한 기본 원리는 이동 평균 필터에서 유래하였다.
1.1 이동평균 필터
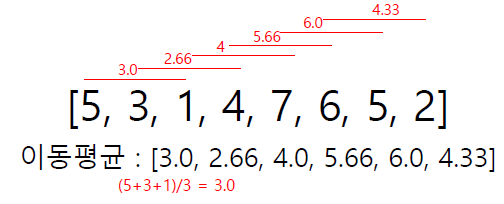위 사진처럼 이동평균을 구현해보자
data = [5,3,1,4,7,6,5,2]
h = 3
mov_avg = [None]
#원본 데이터와 같은 길이를 갖게 하기 위하여
#시작점과 끝점에 각각 'None'를 첨가한다.
for i in range(1, len(data) -1):
cal = sum(data[i-1:i+2]) / h
mov_avg.append(round(cal, 3))
mov_avg.append(None)
print(mov_avg)
위 코드의 출력결과는 사진과 같으며, 이를 그래프로 그리면 아래와 같다.
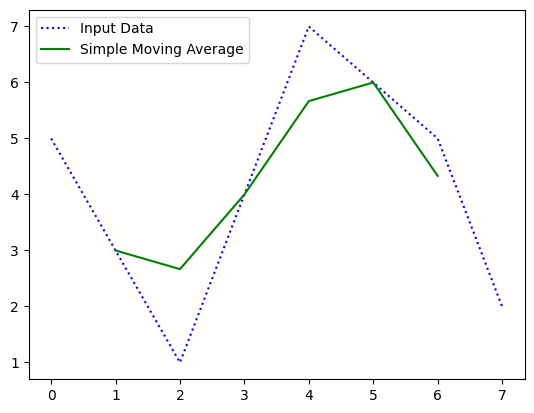시각화 하면 더 명확하게 데이터가 갖는 패턴을 유지함을 알 수 있다.
1.2 가중 이동평균 필터
이동 평균 필터를 응용하면 위 사진처럼 최신 정보 혹은 특정 포인트에 높은 가중치를 주어 이동 평균을 구하는 가중 이동 평균 필터를 만들 수 있다.
data = [5,3,1,4,7,6,5,2]
h = [0.2, 0.3, 0.5]
wm_avg = [None]
for i in range(1, len(data)-1):
cal = np.array(data[i-1:i+2]) * np.array(h)
wm_avg.append(round(sum(cal), 3))
wm_avg.append(None)
print(wm_avg)
위 결과를 원본, 이동평균, 가중이동평균별로 비교 분석하면 아래와 같다
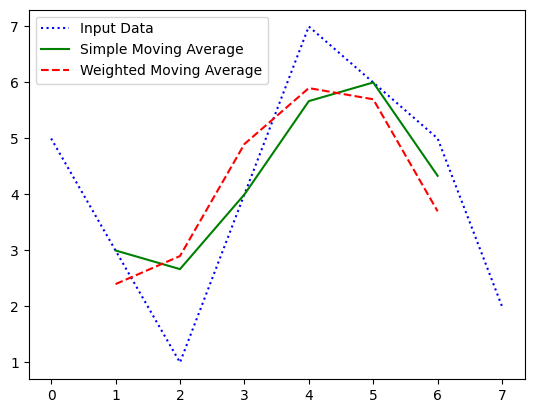
여기서 h = [0.2, 0.3, 0.5]를 커널(필터)로 확장하고 신경망의 weight matrix으로 볼 수 있을 것이다.
1.3 경계 찾기
이 기본적인 weight matrix로 이미지의 edge를 찾는 예제를 한번 만들어 보자
#가중평균 필터를 응용한 엣지 찾기
data = [0, 0, 0, 10, 10, 10, 10, 10, 10, 10, 0, 0, 0]
#일반적으로 'edge는 인접한 지역에서 값이
#급격하게 변하는 현상이 있다
#위 리스트에서는 3~4번, 10~11번에서
#급격한 값의 변화가 있고 여기가 edge지점이다.
h = [-1, 2, -1]
wm_avg = [None]
for i in range(1, len(data)-1):
cal = np.array(data[i-1:i+2]) * np.array(h)
wm_avg.append(round(sum(cal), 3))
wm_avg.append(None)
print(wm_avg)원본 데이터와 edge 검출을 위해 작성한 weight matrix(h)을 시각화 한다면 아래 처럼 급격한 값의 변화가 있는 지점을 쉽게 찾아낼 수 있다.
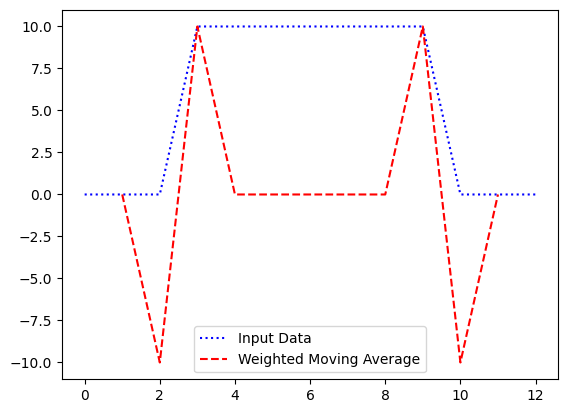
2. 이미지 합성곱
Conv Layer은 필터를 사용해 데이터의 특징을 추출하는 기능을 수행하며, 이때 이미지가 가진 지역적인 패턴을 인식 가능하기에 인식 대상 개체가 위치 및 포즈가 변화해도 인식 성능을 유지하는 장점이 있다.
이때 사용되는 이미지 필터는 입력 데이터에서 특징을 추출하기 위한 요소로써
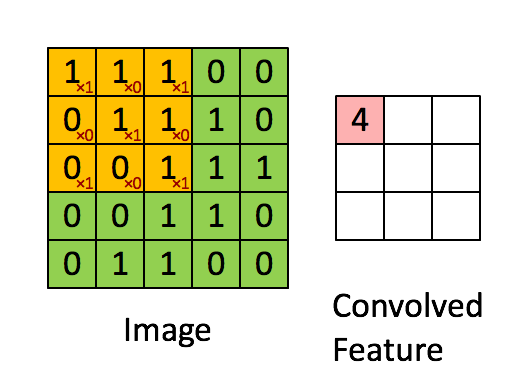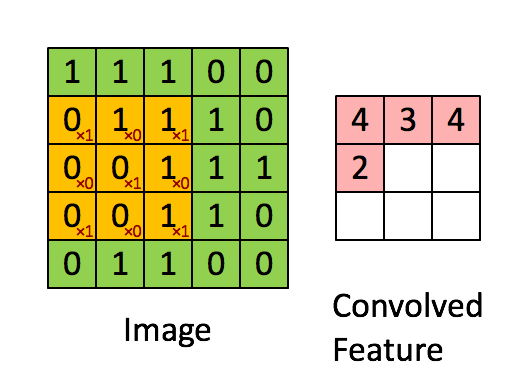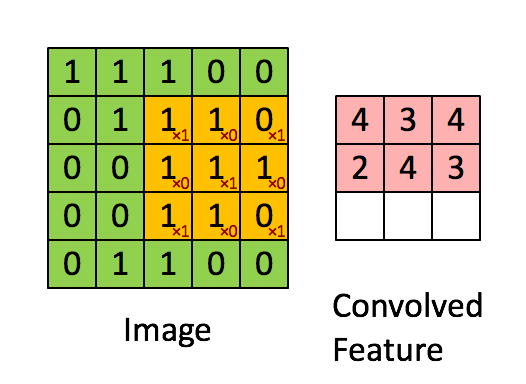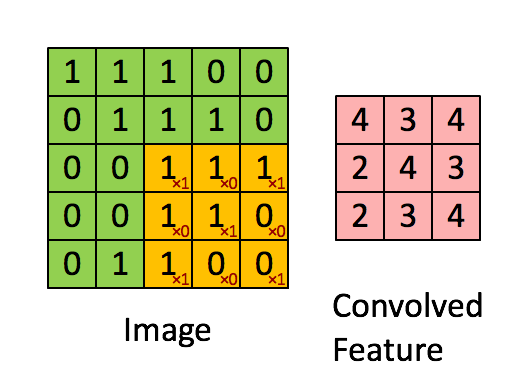위 사진처럼 노란색 행렬(이미지 필터)가 이미지에서 특징을 추출해낸다.
이때 이미지 필터에 적용된 가중치는 Convoled Feature를 출력하는 동안 값이 변하지 않으며(가중치 공유)
작업을 완료하고 다음 작업인 역전파 과정 때 가중치의 업데이트가 이뤄진다.
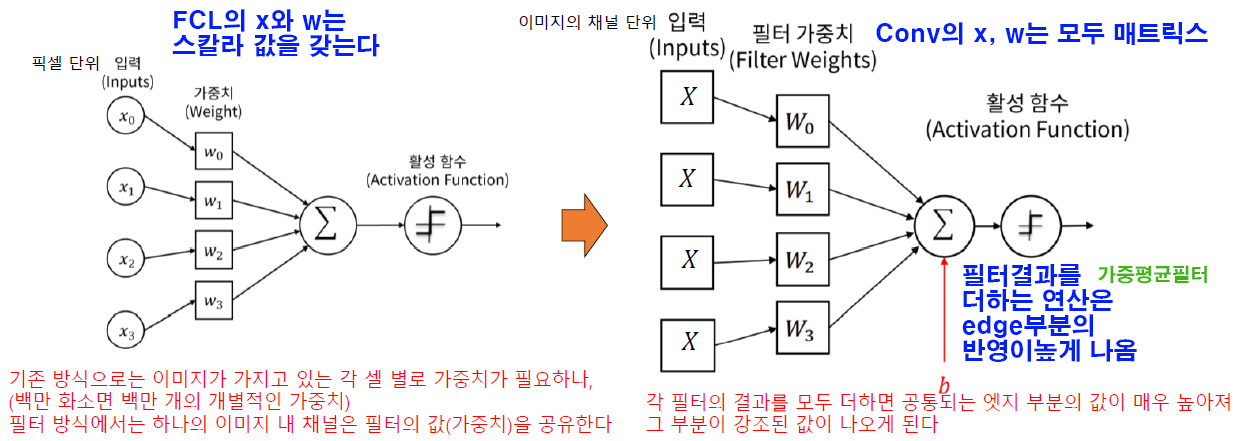w(필터)의 경우 초기값은 random함수로 난수가 배정되지만 역전파 과정을 통해 점차 loss를 0으로 수렴하게 만드는 feature map이 출력되도록 값이 업데이트 된다.
