Concept of Convolutional Neural Network

Receptive Fields

시각 피질 안의 각 뉴런들은 일부 범위 안에 있는 시각 자극에만 반응한다 !

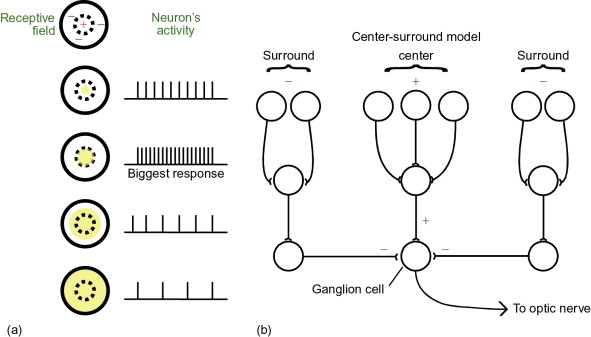
• 각 뉴런들의 receptive field 가 합쳐져서 우리 눈에 보이는 전체 시야를 감싸게 된다.
• 어떤 뉴런은 수평선에 반응하고 어떤 뉴런은 다른 각도의 라인에 반응한다.
• The bigger the receptive field, the more complex the pattern → Higher level 에 위치한 뉴런들은 Lower level 에 위치한 뉴런의 output 에 기반한다.
  • 위 개념을 CNN 에 적용하면, CNN 에서 Lower layer 의 뉴런들과 Higher Layer 의 뉴런들은 weight 를 공유하는 사이라는 말이다.

CNN 에서의 receptive field 란, 입력의 feature 가 영향을 받는 (i.e. feature 에 highly contribute 하는) input space 내의 영역을 뜻한다.

• 이 receptive field 내에서 중앙에 위치한 pixel 일수록 feature 에 더 중요한 역할을 하는 것으로 가정한다.
  

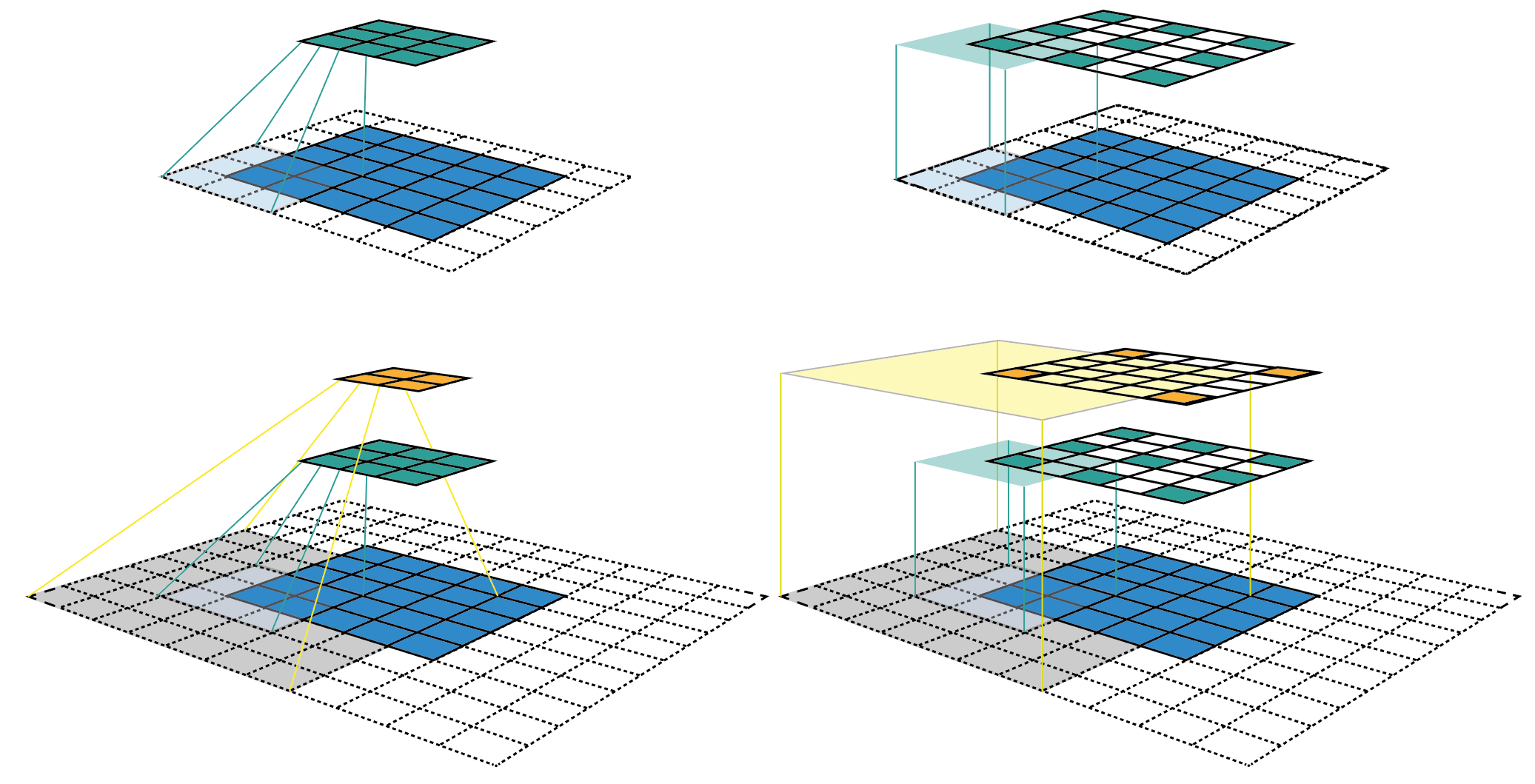
왼쪽의 경우 Feature map size 를 줄여 나가기 때문에 feature 가 계속 dense 하지만, 오른쪽의 경우 feature map size 를 고정하여 점점 sparse 해지게 된다. 이러한 특성 때문에 feature map size 를 줄여나가도 문제가 없는 것이다!

왜 이미지 분류에서는 Fully Connected 기반의 DNN 을 사용하기 힘든가
A. 이미지의 크기에 비례하여 parameter 의 개수가 많아지기 때문. 이는 Hidden layer 를 많이 쌓을 수록 더 큰 문제가 되며 이 때문에 차원수를 줄이고 각 층을 부분적으로 연결하는 convolution filter 의 역할이 중요함.

Convolutional Layer

Convolution Layer 에서 convolution 연산을 수행하는 weight 의 세트를 convolution filter (or convolution kernel) 이라고 부른다. 보통 {3, 5, 7} 의 사이즈를 갖고 있다.

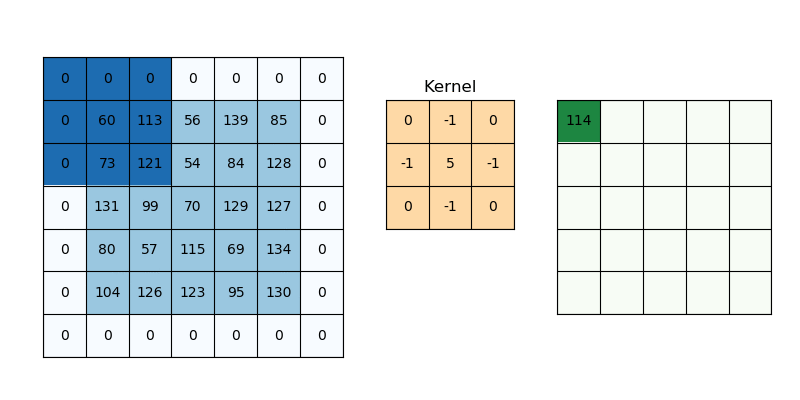
• 5*5 이미지에서 convolution filter 를 사용하여 값을 추출하면 이보다 작은 feature map 을 얻을 수 밖에 없다. 입력과 똑같은 크기의 feature map 을 얻기 위해 이미지의 가장 자리에 zero padding 을 수행하여 임의로 input size 를 늘려주는 작업이 선행된다.
• 언젠가는 feature map 을 줄이는 단계가 있는데 이때는 Stride 를 1보다 큰 값으로 지정하여 receptive field 를 띄엄띄엄 보는 효과를 준다.

CNN 에서의 학습이란?

Horizontal Line 에 대한 feature 를 배우는 filter 를 적용하여 위와 같은 feature map 을 추출할 수 있다. Deep Learning 을 거치면 어떤 filter 를 배워야 할지 일일이 설정할 필요없이 알아서 무엇을, 어떤 weight 로 배워야 할지 설정한다는 것이다.

• 각 레이어에서 Convolution filter 의 개수만큼 feature map 을 생성한다.

Memory Issue

CNN 의 가장 큰 어려움 중 하나는, convolutional layer 가 많은 양의 메모리를 필요로 한다는 점.
(기본적으로 대부분의 경우에 input size 가 크고, Backprop 을 하는 동안 forward pass 에서 계산했던 모든 weight 를 필요로 하기 때문)

예를 들어, AlexNet 의 첫번째 conv layer 에서 필요한 parameter 개수와 연산량은 아래와 같이 계산할 수 있다.

• Output Feature Map size: 55 55 96
• Kernel Size: 11 11 3
• Bias: 96

Number of Parameters

$11\times11\times3\times96 + 96 = 34,944$

만약 fully connected layer 를 사용했다면....?
55x55x3x55x55 = 27,451,876

Number of Calculations

$55\times55\times96\times11\times11\times3 = 105,415,200$

Pooling Layer

parameter 수를 줄이기 위해 input 의 일부만 sampling 하는 것

Pooling Layer 는 가중치 없이 입력값을 간단한 함수를 거치게 하여 변환하는 정도에 그침. 대신 출력값이 입력값보다 훨씬 작은 dimension 으로 mapping 시킬 수 있으므로, 연산량과 parameter 수를 줄이는데에 효과적.

따라서 Conv Layer 뒤에 dimension 을 줄이는 용도로 사용하고 거의 세트로 딸려온다고 해도 무방함.

• Max Pooling: 일정 영역에서의 최대값만 뽑아냄
  • Translation Invariance: 영역의 최대값만을 따지기 때문에 shift 된 이미지라 할지라도 동일한 출력을 생성함.
    e.g.) max([0, 0, 0, 1]) == max([1, 0, 0, 0])
  • 일반적으로는 Max Pooling 을 사용함.
• Average Pooling: 일정 영역에서의 평균값을 뽑아냄

CNN Architecture

첫번째 층을 제외하면 일반적으로는 33 또는 55 필터를 가진 Conv Layer 몇개 + Pooling Layer 1개의 반복적인 구조

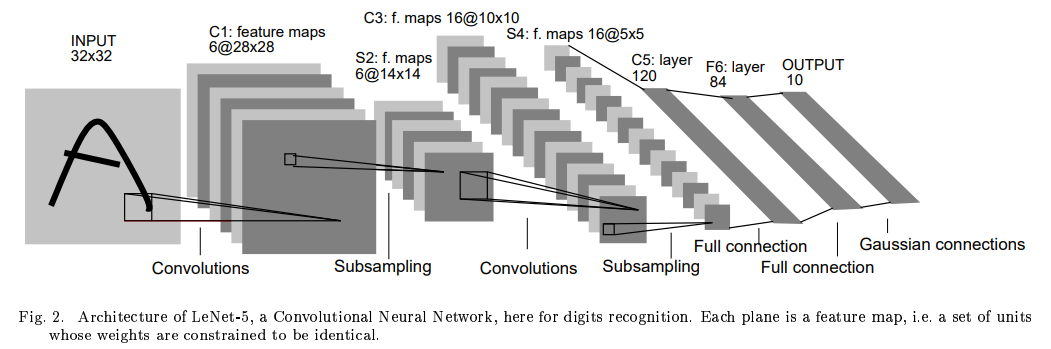
LeNet-5 (1998)

CNN의 조상(?)

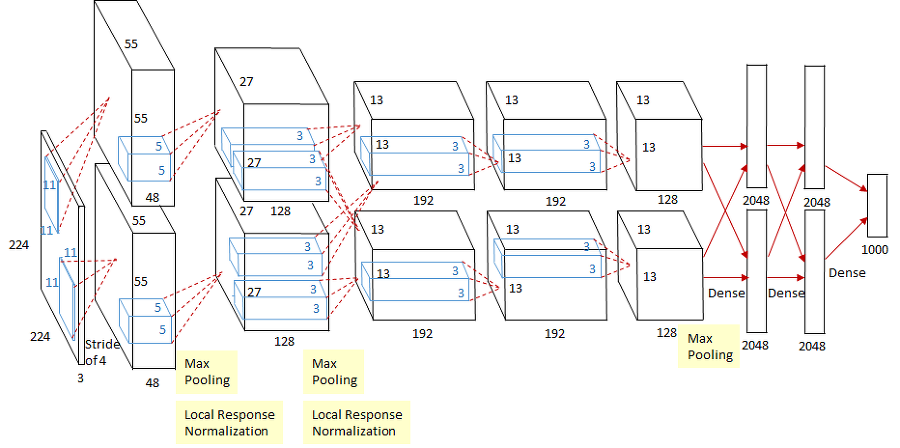
AlexNet (2012)

대 CNN 시대의 시작

의의

• 최초로 convolutional layer 를 연속으로 쌓은 구조
• ReLU activation 이 흥하게 된 계기가 아니었을까
• Data Augmentation 을 수행하여 성능 향상
• 여러가지 Regularization 기법 적용
  • Dropout: 0.5의 비율로 적용했는데 말그래도 뉴런의 반을 누락시킨다는 당시에는 파격적인 구조
  • Local Response Normalization: 가장 강하게 활성화된 뉴런이 다른 특성 맵에 있는 같은 위치의 뉴런을 억제하는 방법.

GoogLeNet (a.k.a Inception v1, 2014)

1*1 convolution filter 를 적용한 inception module 개념을 창조

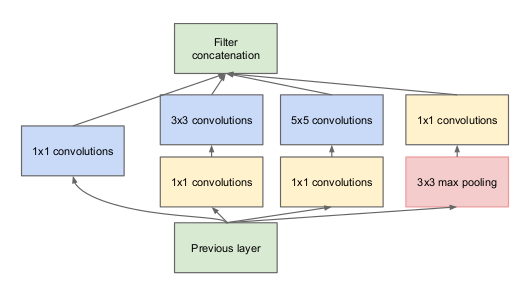
1. previous layer 의 input 이 서로 다른 레이어에 전달됨
2. 각기 다른 크기의 convolution layer 가 서로 다른 패턴을 학습
3. 이때 Stride = 1 과 동일한 패딩 사이즈를 적용하여 출력시 concat 이 될 수 있도록 동일한 출력 사이즈를 갖도록 설계
4. 전체 네트워크의 구조는 몇개의 simple convolutional layer 를 거친 후 이러한 inception module 을 9개 쌓는 구조.

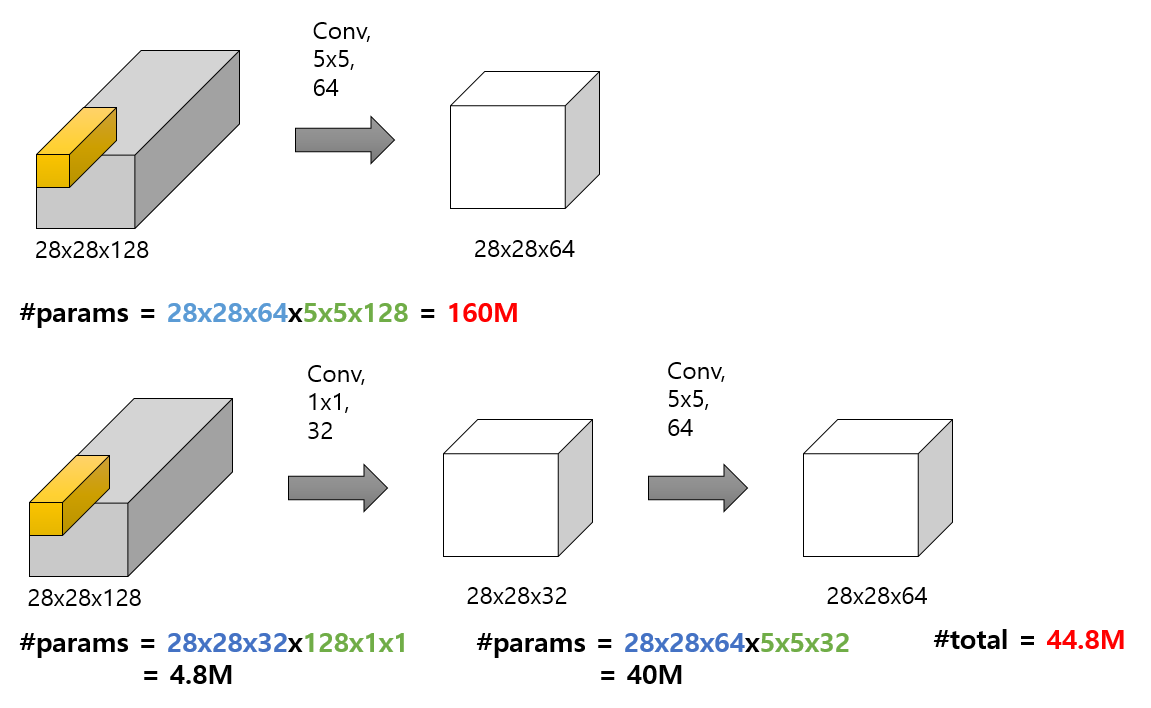
1x1 Convolution (a.k.a Point-wise Convolution)

1 사이즈 이기 때문에 입력의 한 개 픽셀값에 대한 특성을 출력하는 필터라고 이해할 수 있음.

얼핏 들으면 쓸모 없어 보이지만 다음과 같은 장점이 있다.

1. 가로, 세로가 아닌 깊이 단위의 패턴을 잡을 수 있음.

2. feature map 의 개수를 줄여서 parameter 개수를 줄이는 bottleneck layer 의 역할을 담당.

   

3. 3x3 하나를 넣는것보다 3x3 + 1x1 레이어의 조합으로 더 복잡한 패턴도 담당할 수 있음.
   (1*1 필터가 ReLU 같은 non-linear 한 역할을 해주기 때문인 것으로 이해함)

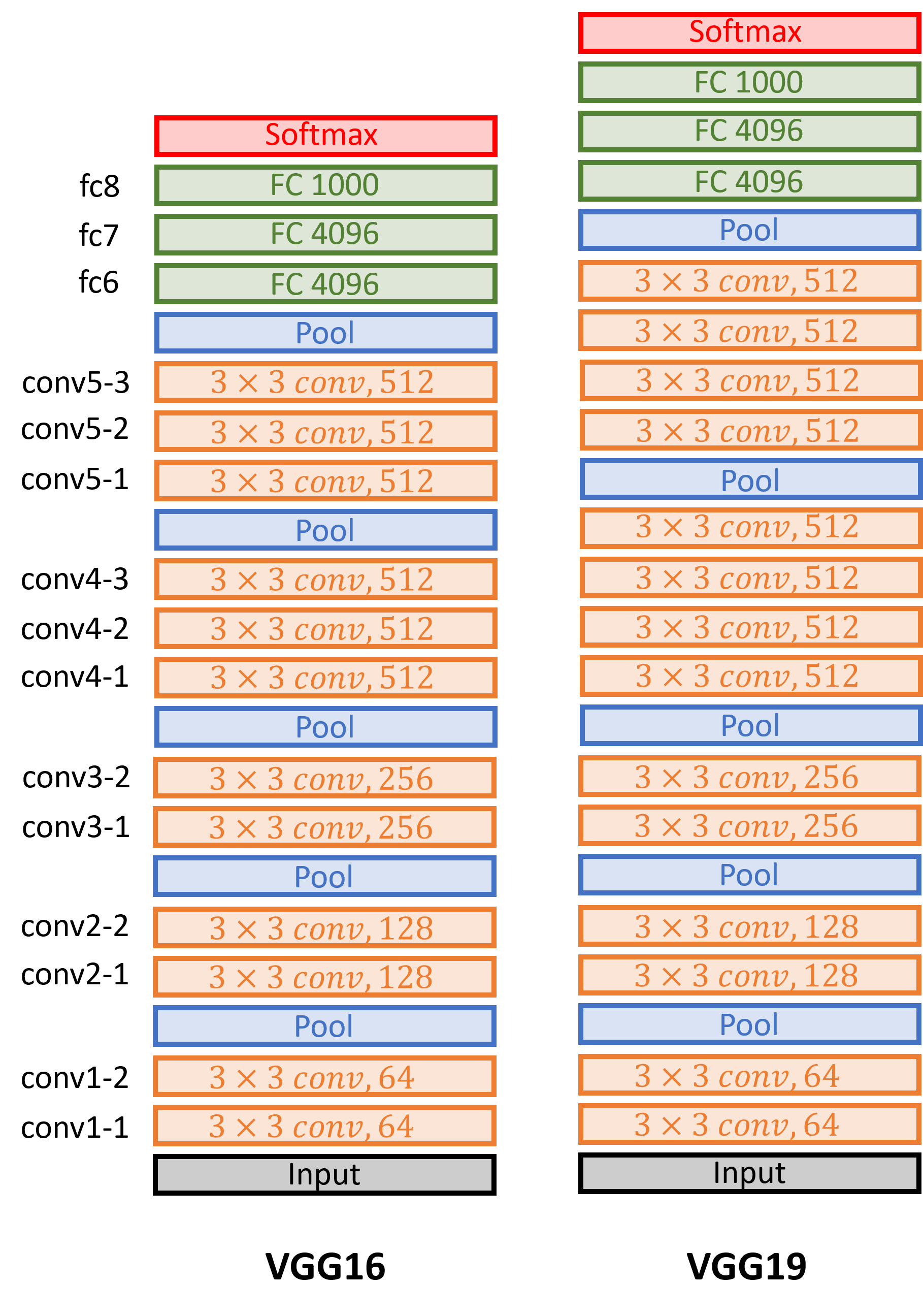
VGGNet (2014)

우리가 생각하는 정석적인 CNN 에 가장 가까운 모델

굳이 특징이라면 FC Layer 에서도 2개의 hidden layer 를 사용했다는 점.

ResNet (2015)

간단한 아이디어로 엄청난 성능 향상을 이루어낸 역사적인 아키텍쳐

당시 hidden layer 를 많이 쌓는 것이 답이 아닌가 라는 방향으로 연구가 많이 진행됐지만 생각보다 그 효과가 크지 않아 어려움이 있었음.

이때 깊은 네트워크를 이렇게 쌓으니 되더라 라는 해법을 제시한 논문

Skip Connection (a.k.a Shortcut connection)

input 이 layer 를 skip 하고 더해진다고 하여 붙여진 이름

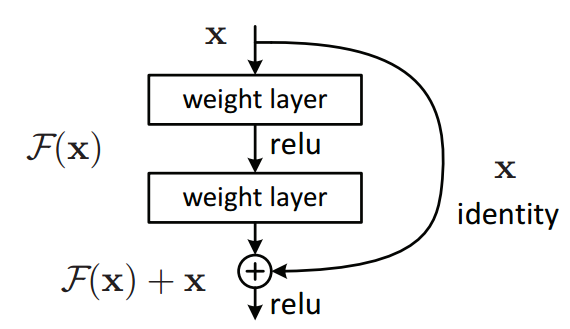
• x를 input 이라 하고 F(x) 가 기대하는 출력값에 대한 함수라고 할 때, 기존의 학습 방식은 올바른 F(x) 를 찾는 것이 목적.
• 그러나 output 에 input 을 더해주어 F(x)+x 의 형태를 얻고자 한다면, input 과 output 의 차이가 없어야 올바르게 학습이 되었다고 볼 수 있기 때문에 F(x) 가 0이 되어 x가 identity mapping 이 되는 방향으로 학습 하게 되는 것.
• x를 F(x)+x 로 매핑하는 함수 H(x) 가 있다고 할 때, min(H(x)-x) 가 학습의 목적이며 yhat - x = residual 이라고 부르는 것과 같이 이와 같은 모듈 구조를 Residual Block 이라고 지칭함.
• Convolution Layer 사용시에 이러한 Skip Connection 구조를 사용하여 전체 네트워크를 구성함.

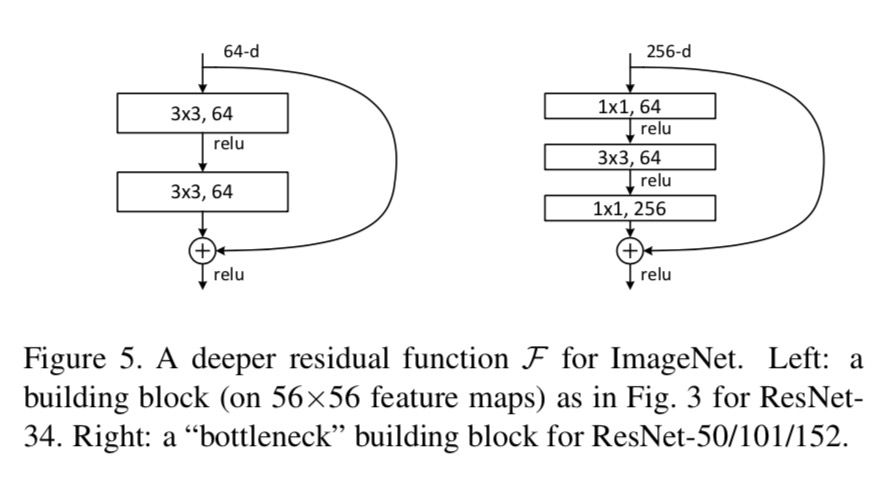
• 입력과 출력을 더할 때 이미지의 H, W가 같아야 더할 수 있는데 Stride = 2 를 사용하게 되면 일정 구간에서 크기가 작아지게 됨.
• 이를 해결하기 위해 이런 구간마다 Residual block 에 1*1 convolution layer 를 추가하여 dimension 을 맞춰주는 bottleneck layer 역할을 부여함.

Xception (2016)

Inception Module 이 왜 성공적이었는가?

일반적인 CNN 에서 처럼 하나의 convolution filter 가 종합적인 특성을 파악하는 것이 아니라, 3x3 과 5x5 가 분리된 구조를 지니면서 Spatial (위치) correlation 과 Channel-wise correlation 을 분리해서 분석하기 때문이다.

그렇다면 Channel 과 Spatial 한 mapping 을 완전히 분리해보자.

Depthwise Separable Convolution

이미지의 각 채널 (R, G, B) 를 분리하여 각각의 채널에 대해 convolution filter 를 적용하고 이를 합치게 됨. 각각의 채널에 대해 적용하기 때문에 input 과 output 의 channel 수가 동일하다.

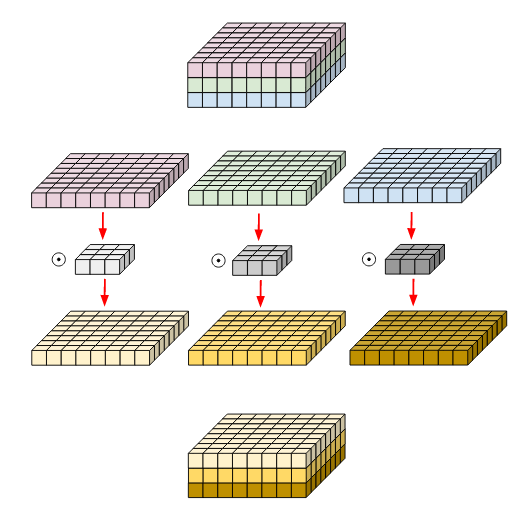
Xception 에서는 이 모듈구조를 활용하는데 두 개의 단계로 나누어서 사용한다.

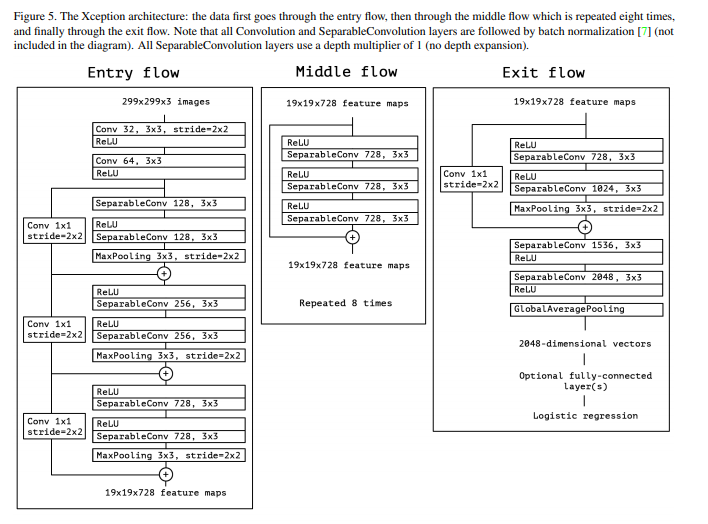
1. 분리된 채널마다 3*3 사이즈의 spatial 필터를 적용
2. 채널 사이의 패턴 학습을 위해 1*1 convolution (channel-wise) 필터를 적용

Separable convolution 을 사용할 때 입력 이미지에 바로 사용하게 되면 채널이 3개밖에 없으므로 최초에는 일반적인 conv layer 를 거쳐서 채널 수를 늘려주는 작업을 수행한다.

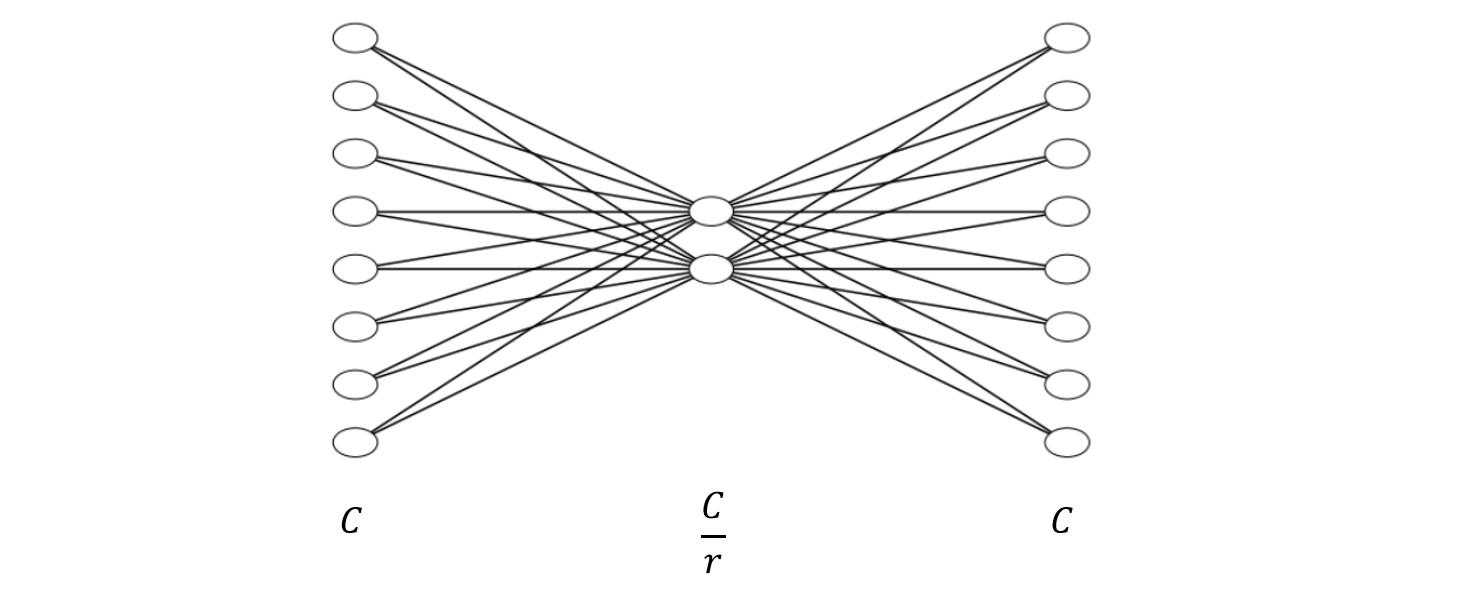
SENet (2017)

어느 아키텍쳐에나 적용할 수 있는 SE block 을 개발

Squeeze Operation

채널의 중요한 정보만 짜내는(?) 연산 → 어떤 특성이 일반적으로 가장 크게 활성화 되는지를 학습하는 것

이 짜내는 연산의 방법으로 Global Average Pooling (GAP) 을 사용하여 채널마다의 평균값을 계산함.

Excitation (Recalibration)

GAP 으로 얻은 맵을 훨씬 작은 차원에 매핑하고 이를 다시 이전 feature map 의 개수만큼 calibration 값을 출력함.

이러한 과정을 통해 얻은 calibrated vector 를 feature map 과 곱하여 관련 있는 특성의 값은 높이고 관련 없는 특성의 값은 낮추는 효과를 얻을 수 있음.

Object Detection

Predicting Bounding Box

물체의 위치를 찾는 것은 물체 주위의 bounding box 를 찾는 문제로 풀이하는데, 일반적으로는 물체 중심의 x, y 좌표와 박스의 너비, 높이를 예측하는 과정임.

이는 이미지 분류와 달리 숫자를 맞추는 문제로서, regression 을 수행하여 값을 예측함.

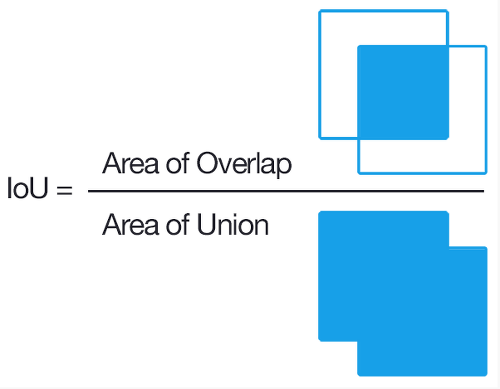
Bounding Box 에 대한 evaluation metric 으로 IoU (Intersection over Union) 이 흔하게 사용됨.

Box 의 클래스를 평가하기 위한 metric 으로는 mAP (mean Average Precision) 이 사용된다.

1. 하나의 클래스에 대해 recall-precision trade-off 를 이용하여, recall 을 0.0~1.0 까지 늘렸을 때 max precision 값의 평균을 계산.
2. 모든 클래스에 대해 1번을 수행하고 이에 대해 다시 평균을 계산.

Detection in general

일반적으로는 다음과 같은 스텝으로 이루어진다.

1. 이미지를 일정한 grid 로 나눈다.
2. Convolution filter 가 Sliding Window 방식으로 이미지를 훑으면서 각 Grid 마다 target object 가 있는지 없는지를 찾는다.
3. 객체 크기가 다를 수 있기 때문에 서로 다른 필터가 서로 다른 크기의 물체를 각자 찾는다.
4. 각 grid 마다 탐색된 bounding box 를 줄이는 작업을 수행한다 (Non-max suprresion)
   • NMS: threshold value 이하의 bounding box 를 모두 삭제하며 가장 높은 점수를 지닌 박스와 많이 겹치는 다른 박스들을 모두 제거.
5. 박스에 대한 클래스를 분류한다.

YOLO (2015, 2016, 2018)

앞선 방법과 달리 이미지를 여러번 나누어 보는 것이 아닌 한 번만 본다고 해서 You Only Look Once

물체가 있는 곳을 먼저 따는 Region Proposal Network 에 클래스를 분류하는 Classifier 를 붙인 2-stage 방식이 아니라 하나의 영역에서 한 번에 box와 class를 얻어내는 최초의 1-stage detector 라는데에 큰 의의가 있다.

1. 물체에 대한 대략적인 대표 크기를 지닌 Anchor Box 를 설정한다. 이는 ML 알고리즘으로 찾을 수도 있고 그냥 간단하게 설정할 수도 있다.
2. 학습하면서 Anchor box 의 크기를 얼마나 조정해야 타겟에 적합할지를 예측함.
3. 하나의 이미지에 대해 N개의 grid 를 생성하고 각 grid 마다 정해진 개수의 bounding box 를 생성한다.
4. Bounding Box 를 예측할 때 박스의 중심이 grid 안에 놓인 것만을 예측하도록 훈련된다.
5. 이때 각 grid 에서 물체에 대한 bounding box 와 분류한 클래스의 확률을 한 번에 예측한다.

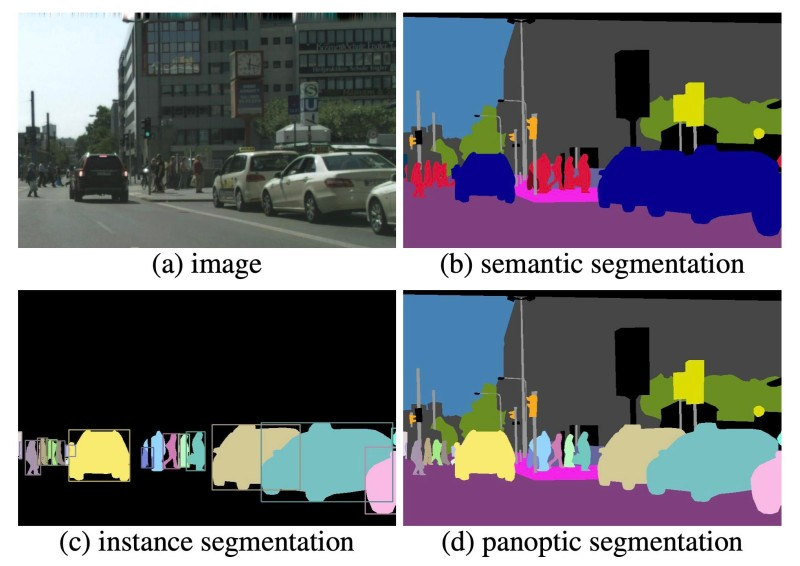
Semantic Segmentation

Segmentation 종류에는 우리가 아는 Pixelwise Classification 의 형태만 있는건 아니다.

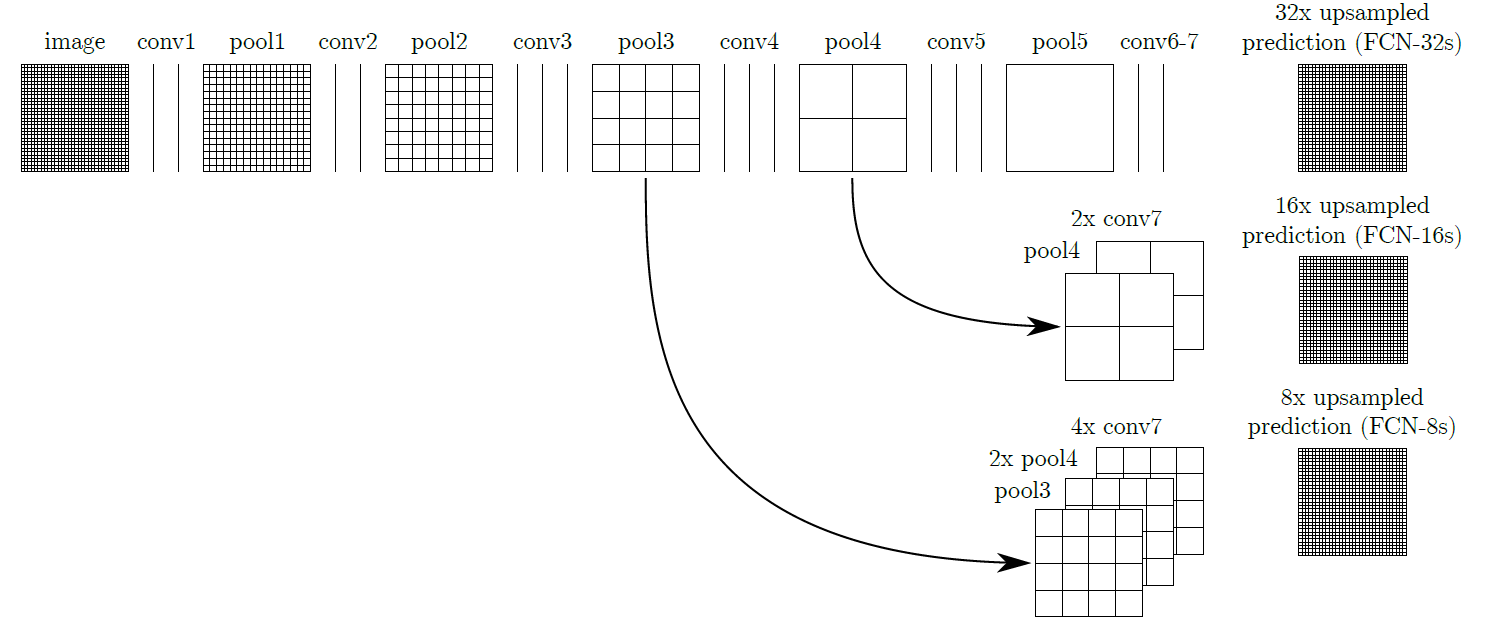
FCN

Fully Convolutional Network. 즉, 모든 레이어를 convolution 으로 대체하겠다!

Segmentation 에서 기존 네트워크 구조의 한계

• Fully Connected Layer 에 들어가는 input 이 Flatten 된 형태로 들어가다보니 이때 위치정보가 사라지게 된다.
• 물체의 class 만을 파악하는데는 문제가 없지만 위치를 파악해야 하는 task 에서는 사용할 수 없다.

Dense 층을 Conv 층으로 대체했을 때의 장점

• 위치 정보를 보존할 수 있다.
• 이미지 크기에 제한이 없다.
  • Dense 층에서는 입력 크기에 대해 정해지는 뉴런의 개수가 존재한다.
  • 서로 다른 이미지 크기에 대해서는 마지막에 출력되는 feature map 의 크기가 달라진다.

Upsampling Layer (a.k.a Deconvolution)

Convolution 연산이 특징을 추출하여 최종적으로 압축된 feature map 을 뽑아내는 역할을 수행했다면, Upsampling 연산은 추출된 feature map 을 바탕으로 크기를 키워주는 역할을 한다.

Upsampling 의 방법으로 일반적인 interpolation 방법보다는 Transposed Convolutional Layer 를 사용한다.

• Convolution Matrix 를 transpose 하여 연산하기 때문에 이러한 이름이 붙었다.
• 수학적 이해를 원하면: https://zzsza.github.io/data/2018/06/25/upsampling-with-transposed-convolution/

Skip Combining

위와 같은 upsampling 은 해상도 확장에 있어 좋은 역할을 수행하지만 작은 feature map 에서 키운것이기 때문에 디테일이 떨어질 수 있다.

이를 보완하기 위해 convolution 연산을 수행할 때 같은 단계에 있던 feature map 을 가져와서 더해주는 작업을 거친다.