Generation - 2

TOLL TERRY·2024년 2월 21일

업스테이지AI_패스트캠퍼스

upstageAI_패스트캠퍼스

목록 보기

16/20

생성 모델 평가 지표의 필요성

판별 모델의 종류
정답(GT)가 존재하므로, 모델의 출력을 정답과 비교하기 용이
범주형 데이터를 사용하는 경우 분류문제와 연속형 데이터는 회귀문제

평가지표

범주형 데이터

정확도

각 클레스별 데이터의 정확도 accuracy를 평가함.

f-1 score

각 클래스별 데이터가 불균형한 경우엔, 정확도만으로 평가하지 않고 정밀도, 재현율, f-1score(정밀도와 재현율의 조화평균)를 이용함.

연속형 데이터

MSE(유클라디안거리), MAE(맨하튼 거리)

회귀 분석에서는 실제 값과 모델이 예측한 값의 차이를 기반으로 평가함.

결정계수(R-squared), 상관계수(corrlelation)

주어진 데이터의 값의 범위가 다른 경우, MSE와 MAE만으로 평가할 수 없음.

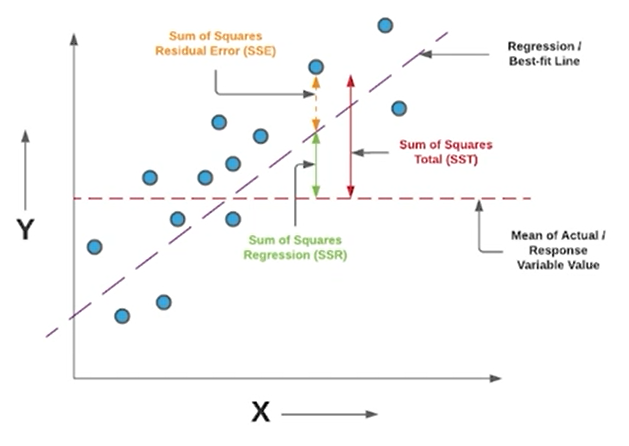
위와 같이 데이터의 1000개의 중에 100개, 100개 중에 10개를 틀린다면, 둘다 0.1프로만큼의 차이가 발생한다는 점을 MSE, MAE만으로는 평가하기 어려움.

생성 모델 평가의 어려움

판별 모델과 달리 비교할 정답이 존재하지 않아, 결과를 직접적으로 비교할 대상이 없음.
학습 데이터를 정답으로 사용할 경우, 학습 데이터를 그대로 복제하는 현상이 발생함.

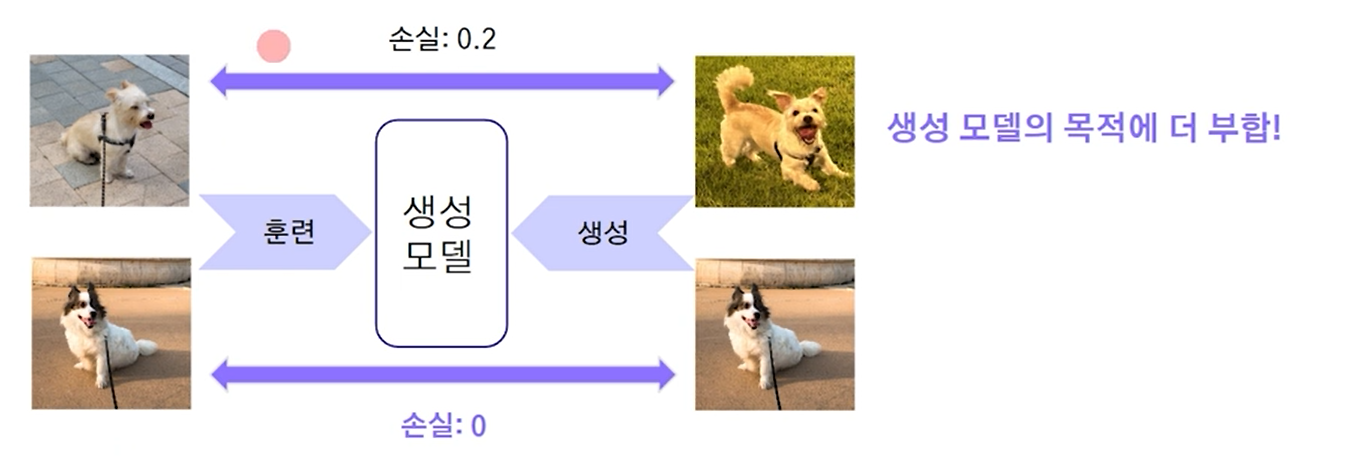
위와 같이 학습데이터에만 학습할 경우 손실이 차이가 안나게 되면, 그냥 학습데이터의 복제가 이루어지므로, 생성 모델은 윗사진이 더 잘 만들었다고 볼 수 있음.
사람을 활용한 생성 모델 평가 방식(사람이라는 인건비, 시간 등등의 비용이 많이 들음)

생성 모델의 평가 (품질과 다양성 2가지 관점)

품질(충실도 Fidelity 이미지의 품질)
다양성(Diversity 이미지의 다양성)

생성 모델 평가 지표 - 6가지

단순한 방법 : 학습에 사용한 원보 데이터와 생성된 결과물을 비교
-- 픽셀 거리 (생성 모델에 동작이 잘 안되는 경향이 있음)
-- 특징 거리 (IS)

Inception Score(IS)

Inception v3 모델을 분류기로 이용하여, GAN을 평가하기 위해 고안된 지표
예리함(Sharpness)과 다양성(Diversity) 두가지를 고려함.

예리함이 적으면 블러리(흐려짐), 높으면 선명함

무질서도(Entropy)

예리함과 다양성 지표는 무질서도(엔트로피)로 해석 가능함.
무질서도가 높다면, 임의의 변수 x에 대해 예측되는 y의 값이 많다. (예측이 어려움), 확신이 없음
무질서도가 낮다면, 임의의 변수 x에 대해 예측되는 y의 값이 적다. (예측 가능함), 확신이 있음

주사위의 무질서도가 더 높음. (동전의 앞뒤를 예측보다 주사위 숫자 예측을 맞추는 것이 더 확률이 낮다)
동전 : 앞뒤 나올 확률 1/2 :: log 2 ( -1/2 log 1/2 - 1/2 log 1/2 = -1 log 1/2) -> 2번곱셈
주사위 : 각 숫자 확률 1/6 :: log 6 ( -1/6 log 1/6 ...... = -1 log 1/6) -> 6번곱셈

예리함

특정 숫자를 생성했을때, 숫자 분류기가 제대로 인식한다면 좋은 예리함을 가진 데이터를 생성한 것.
어느 클래스인지, 확신을 못가지고 있을때, 선명하게 된 이미지를 잘 분류가 가능하므로 모델 예측의 엔트로피가 낮게 나오는 것이 더 선명하고 높은 품질의 영상이라 볼 수 있음.

다양성

좋은 품질의 데이터를 생성하는 것만큼 다양한 데이터를 생성하는 것.
다양성이 높은 모델은 maginal에 엔트로피가 높게나옴(=무질서도가 높음), 분포가 uniform 분포에 가까워질수록 무질서도가 높아지게 됨. 즉 분포가 uniform하게 된다면, label(타겟, class)를 무엇이라고 나올지 예측이 어려워지므로, 엔트로피가 높아짐.

IS의 계산

정보 엔트로피를 계산하는 것은 확률에 의존하게 되므로, 이는 확률을 나타내는 지표로 이미지넷 classifier를 사용하게 된 것임. 입력에 대해 특정 class에 속한 확률을 의미함.
IS의 곱으로 이루어져 있으므로, 이는 두 확률 분포의 KL-Divergence를 계산하는 것과 동일하게 됨. (선명하면 특정 class로 분류될 확률이 높음), (다양하면 모든 class로 고르게 분포가 됨을 활용함.

한계점

학습 데이터셋과 다른 데이터를 생성하는 경우 제대로 평가하기 어려워짐.
예시 (얼굴사진으로 class로 분류될 확률이 아닌 것들의 데이터 셋이라면 평가가 불가능해짐.)
사람의 얼굴을 만들경우, 모두다 그냥 사람으로만 분류하게 됨.
IS가 높은 데이터를 생성하면 계속 같은 데이터를 생성함. (오로지 생성된 데이터만을 이용하여 계산됨.) - 품질이 높은 데이터로 계속 만들어도 좋은 점수를 반환하는 한계점. 혹은 각 class별로 이미지를 1장씩만 똑같이 많이 만들어도 다양성을 굉장히 높게 평가하는 한계가 있음.
이외에도 기울기 기반 공격, 리플레이 공격을 통해 점수 조작이 가능함. (노이즈가 많아 객체(class)라고 볼 수 없음에도, IS점수가 높게 나옴)

Frechet Inception Distance(FID)

생성된 데이터의 특징 벡터를 이용하여 학습 데이터와의 거리를 계산함. (낮을 수록 더 좋음)
IS와는 다르게, 분류기를 활용하지 않고, 특징 추출기로만 사용함.
IS의 문제점, 데이터의 확률 벡터가 아닌 특징 벡터만을 활용하게 됨.

학습 데이터와 생성 데이터 모두 활용함. (IS는 생성 데이터만 활용함)
특징들의 Mean과 Variance(분산)을 측정하여, FID 거리를 계산한다.
먼저 Mean값 간의 L2 거리(유클라디안) 측정 + 분산을 활용해서 Tr를 계산함.

한계점

FID점수는 품질(충실도 : Fidelity)와 다양성(Diversity)를 각각 평가할 수 없음. (즉, 품질이 좋은 것인지, 다양성이 강조된 모델인지, 모두다 균형잡힌 것인지 모름)

개선된 정밀도, 재현율

정밀도 : 모델이 positive라 예측 했을때, 실제로도 True인거
생성된 데이터 기준에서, 실제 데이터 분포에 가까운 데이터 (얼마나 품질이 좋은가)
재현율 : 실제 True일때, 모델도 positive인거
실제 데이터 중에서, 생성된 데이터 분포에 가까운 데이터 (얼마나 다양성 좋은가)

분포의 겹친 부분을 계산하는 방법

Close to (근방)
반지름 r인 범위 내에 존재하면 근방에 속하는 데이터로 간주함. 있으면 1, 없으면 0

개선된 정밀도 계산

판별모델에서 정밀도 = (TP) / (TP + FP)
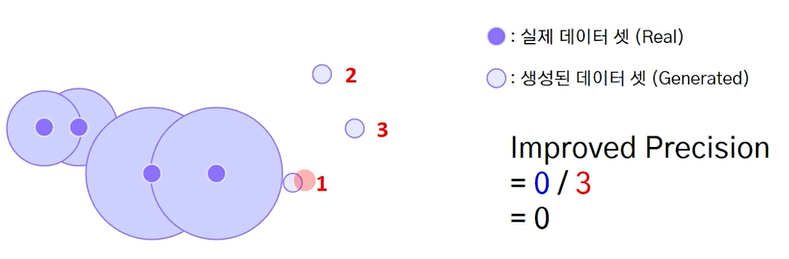
생성모델에서 개선된 정밀도 = 실제 데이터 분포 내의 생성된 데이터 / 생성된 데이터
(생성된 데이터) 중에서 (실제 데이터 분포에 속하는 생성된 데이터)의 비율
그림에서는 실제 데이터셋 근방에 들어간 데이터 1 / 생성된 데이터 3 = 1/3 (0.3333)

개선된 재현율 계산

판별모델에서 재현율 = (TP) / (TP + FN)
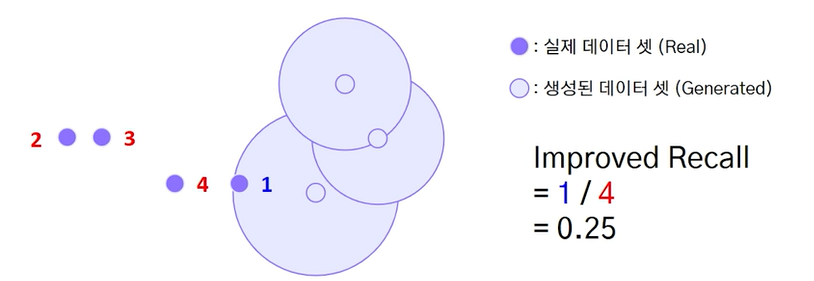
생성모델에서 개선된 재현율 = 생성된 데이터 분포 내의 실제 데이터 / 실제 데이터
(실제 데이터) 중에서 (생성된 데이터 분포에 속하는 실제 데이터)의 비율
그림에서는 생성된 데이터 분포에 실제 데이터 3 / 실제 데이터 4 = 3/4 (0.75)

한계점