생성모델

---

1. 고전 생성모델

• 데이터는 저차원의 필수적인 정보로부터 생성 가능하다는 가정하에 분포를 학습.
• 확률 분포 추정(가우시안 혼합, 볼츠만, 심층, 자기회귀망)

1. 가우시안 혼합모델

• 여러개의 가우시안 분포를 바꾸면, 주어진 데이터에 fitting 되도록 함.

2. 볼츠만

• 신경망의 형태로, 특징추출과 비슷하며, 에너지가 낮을 수록 확률 밀도 함수의 값이 커짐.

3. 심층

• 볼츠만 머신을 쌓은 것임. 입력-아웃풋-입력-아웃풋의 형태를 이루어짐.

4. 자기회귀

• 현재 픽셀값을 이전의 픽셀값에 의거하여 데이터를 추정하게 됨.
• 마르코프 체인의 영향을 받아, 현재 픽셀은 이전 픽셀의 영향을 갖는다.

---

2014년 딥러닝 기반의 생성모델의 등장과 발전

VAE

• 선명하기 보다 흐린 영상을 가지게 된다는 단점.

PixelR/CNN

GAN

• 적대적 생성 신경망(안경 사진 latent vector + 성별 여자 latent vector)의 산술계산으로 여자 선글라스 사진을 얻어낼 수 있었다.

---

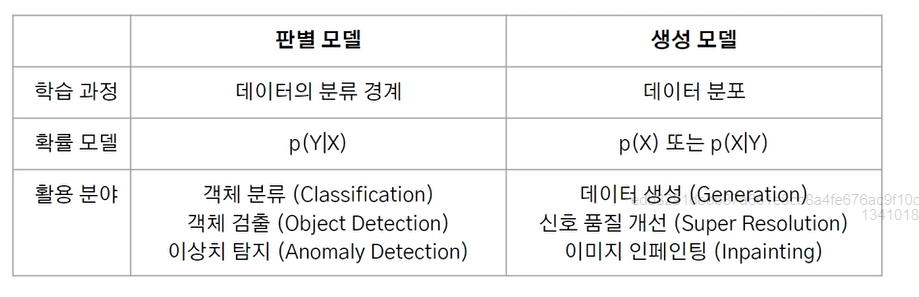
2. 판별 모델과 생성모델

1. 판별모델

• 데이터 x(이미지)가 주어졌을때, 타겟Y(Class)가 나타날 조건부 확률을 직접적으로 반환하는 모델

• 학습중에 데이터 사이의 경계를 예측할 수 있음

• 로지스틱 회귀분석(판별 모델)
  두 그룹의 경계를 곡선으로 판별함.

판별 모델의 활용

• 서로 다른 클래스를 분류
• 이상치 감지하는 문제

2. 생성모델

• 데이터x와 특성 y의 결합 분포, 주어진 y가 없는 경우 데이터의 주변분포 p(x)를 추정함
• 주어진 데이터를 통해 데이터 분포를 학습함.
• 1은 일직선, 0은 곡선으로 이루어진다는 특성으로 분포가 이루어짐.

생성모델의 예시

• 가우시안 혼합 모델
  
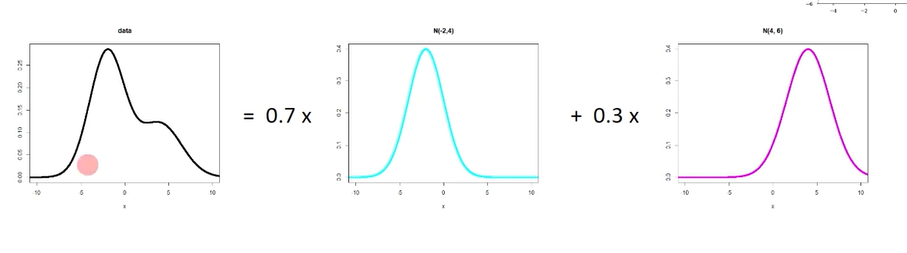
  위와 같이 2개의 정규분포로 오른쪽의 weight=0.3를 주어 y를 맞출 수 있음

어려움

• 복잡한 모든 특성의 분포를 알아야함.(어른 + 안경 + 남성 + 검은 머리 등등의 특성이 필요함)
• 평가지표(강아지 판별은 정확도가 나오지만, 사람과 얼굴 생성시 잘 생성된 것은 어떻게 얘기해야 하는 지, 사람마다 객관적인 지표가 필요함)

생성모델의 활용

• 이미지의 품질 개선 (안경 추가, 헤어 변경)
• 맥락에 맞게 이미지 빈 공간 자동완성

---

3. 생성모델의 실생활 응용 활용사례

화질 개선

• 저화질 영상의 화질을 개선함. (눈, 머리카락의 선명도, 노이즈)
• 오래된 사진 복구.(다양한 잡음이 낀 영상을 깔끔한 이미지로 복원가능)
• AI 프로필(10~20장 기반의 프로필 생성)
• webtoon ai painter(만화 케릭터의 채색을 자동으로 채색하는 툴, 스케치)
• 상품 사진 생성(전문가급 상품 사진으로 변환해주는 제품)
• 가상 옷 피팅(주어진 옷을 사람과 합성하는 기술)

---

4. 생성모델과 최대가능도 추정법

1. 생성모델

• 주어진 데이터를 통해 데이터 분포를 학습하는 모델. p(x|y)

2. 가능도

동전 던지기로 최대 가능도. 10번 던지면 앞7, 뒤3 이라면, 관측의 의거하여 앞은 70% 뒤는 30%로 볼 수 있다. 특정 분포를 따르는 관측들을 토대로, 현상을 설명하는 모델이 얼마나 잘 설명하는가의 지표를 최대가능도라 할 수 있다.

보통 log 최대가능도를 사용하는데, 기존 최대가능도는 곱셈연산이므로 log를 통해 합연산으로 변환하여 사용한다. - 미분 계산이 쉬움(해석쉬움)

1. 최대가능도추정법(MLE)

• 가능도를 최대화하는 파라미터 $\theta$를 찾는 방법임.
• 가능도 함수의 미분을 통해 계산함.

1. 동전 던지기 예시

동전 앞 7, 뒤 3
파라미터 $\theta$ : 동전을 던질 때 앞면이 나올 확률
확률 질량함수 : p(앞;$\theta$) = $\theta$, p(뒤;$\theta$) = 1-$\theta$
가능도 최대화 = 어떤 $\theta$에 대해 앞면 7번, 뒷면 3번이 나올 확률이 가장 큰가?

가능도 : L($\theta$) = $\theta^7(1-\theta)^3$
앞면이 60% = 0.001279
앞면이 70% = 0.002223 -- 가장 큼!
앞면이 80% - 0.001677

앞면이 나올 확률의 추정값 = 0.7

3. 생성 모델의 학습

• 데이터의 분포 $p_{data}$를 어떻게 모델링할 것인가 ? --> 이를 다시보면 모델 $p_\theta$를 어떻게 학습?
  • 해결방법 : 데이터의 분포 $p_{data}$와 모델 $p_\theta$를 가깝게 하자.

1. KL-Divergence(쿨백-라이블러 발산) 최소화

• 두 분포 (데이터의 분포 $p_{data}$와 모델 $p_\theta$)사이의 거리 -> kullback-leibler Divergence)
  

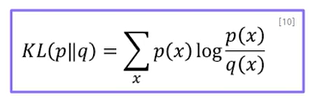
• 분포간의 차이로 볼 수 있음. KL-Divergence(쿨백-라이블러 발산) 최소화 == 로그가능도 최대화로 해석함.

• 앞의 식은 $\theta$에 영향이 없으므로, 제거하여 해석가능함.

2. 어려움

• 우리는 데이터의 분포 $p_{data}$를 모르고 관측된 x1, x2, xn만 관측함.

5. 정리

• 생성 모델의 학습은 최대 가능도를 최적화하며 진행할 수 있음.
• 쿨백-라이블러 발산은 최대 가능도 최적화에 활용가능한 기준이 됨.
• 데이터의 정확한 분포를 알 수 없기에, 바로 적용하기에는 어려움이 존재함.