오토 인코더의 이해 - 잠재표현
-
오토인코더는 새로운 데이터를 생성하기 보다는 비지도학습을 통한 특징추출을 하는 방법.
-
인코딩을 진행해준다. (용량 줄이기, 변환 해주기, 입력 데이터를 받아 N차원으로 데이터 변환후 입력 데이터와 동일한 차원으로 다시 복원하는 과정임.) N차원은 차원축소로 볼 수 있음.
-
N차원(low - 차원)을 잠재표현(= latent표현, = mapping)라 표현한다.
1. 디노이징 오토인코더
- 입력 데이터에 랜덤한 노이즈를 주입, 혹은 Droput 레이러를 적용하여, 노이즈가 없는 원래 데이터로 재구성하는 것.
- 노이즈가 끼인 것을 깔끔한 이미지로 적용하도록 하는 것을 의미하게 된다.
- 안개 속에서 멀리 있는 물체를 구별하려면 -> 데이터의 특성들을 더욱 정확한 학습함.
- 노이즈에 강건한 latent표현
2. 오토 인코더의 활용
- 특성추출, 이상치 탐지
1. 특성 추출기로의 활용
- 학습한 오토 인코더의 인코더 부분을 특징 추출기로 활용.
- latent표현으로 분류, 클러스터링 문제 해결.
- 레이블(클래스)없이도 분류가 가능하다는 점의 장점.
2. 이상치 탐지
- 이상치는 재구성시, 평균제곱오차가 크게 나올 것으로 특정 임계치(Threshold)를 넘으면 이상치로 판단함.
변분 오토 인코더의 이해 - 잠재변수
- 오토 인코더와 마찬가지로 인코더와 디코더를 가지는 생성 모델
- 데이터는 저차원의 잠재변수로부터 생성되며, 이때 잠재변수(z)가 표준정규분포를 따른다고 가정을 가지게 됨.
- 오토 인코더와 변분 오토 인코더의 차이는 잠재표현과 잠재변수의 차이가 발생한다. 잠재변수는 잠재표현의 고정된 것이 아니라 특정 확률 분포를 가진다는 차이가 발생한다.
- 이는 우리가 인코더 x로부터 나온 z(잠재변수)인 정규분포(mean 0,0으로부터 분산 1)로부터 디코더를 통해서 아웃풋 x'의 분포를 "원하는"분포로 변환할 수 있다는 것이다.
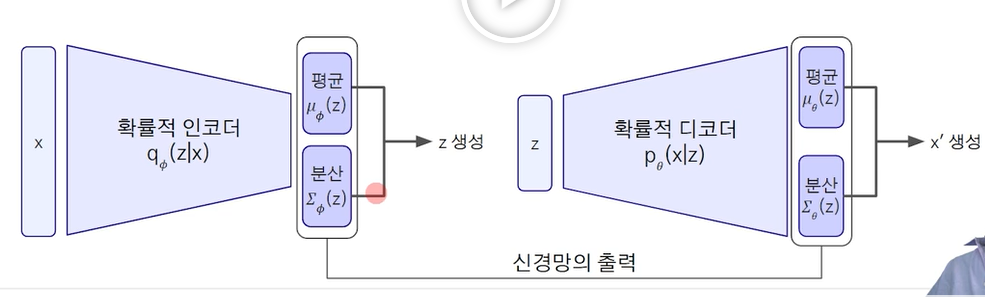
- 이처럼 우리는 잠재표현이 표준정규분포를 따르는 가우시안 분포를 따르게 된다는 점에 차이가 발생한다.
변분 오토 인코더의 학습
- ELBO
- 미분계산이 가능하도록 해주는 재매개변수
입력을 표준정규분포를 따르도록 잠재변수로 만드는데, 이는 강제적으로 각 특징(잠재표현)을 특정 확률 분포로 만드는 것을 의미한다. 이는 평균과 분산을 알고 있으며, 가우시안을 따르도록 만들게
된다. 데이터의 평균은 고정된 상태에서, 분산에 따라 데이터를 샘플링을 진행하게 된다면 분산에 따른 데이터를 생성하게 된다는 것
1. ELBO(Evidence of Lower BOund)
-
현재 우리가 알고싶은것은 p(x)으로 데이터 분포 자체는 알고 싶지만, 직접 계산하는 것이 불가능하다. 따라서 주어진 데이터를 기준으로 우리가 알아내고 싶은 p(x)는 "현재 데이터를 잘 설명하는 분포"를 의미함.
-
예시) 동전 앞면이 나올 확률을 알아내고 싶다면, 앞7 뒤3 --> 현재 우리가 가진 데이터(관측)에 따라 동전의 앞면이 나올 확률 는 현재 모델이 우리가 가진 현상을 얼마나 잘 설명하는 가능도(Likelihood)를 통해 직접 계산은 어려우니, 간접적인 계산으로 최대화 하는 것이다.
-
수식 1
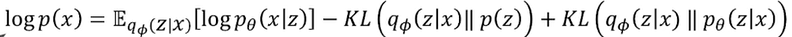
-
수식 1에서 p(x)에 log를 하여 3개의 항으로 표현할 수 있다. 여기서 마지막 항은 쿨백-라이블러 발산 0, 발산은 0보다 크거나 같아야 함으로 계산이 불가함(사후 분포로, 이는 실제 데이터 분포가 주어졌을때, 그것이 정규분포로 표현되었는 지까진 알수가 없음.)
-
수식 2
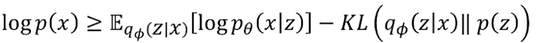
-
수식 2처럼 마지막 항을 제거하여 ELBO로 표현함. 여기서 lower bound라 표현한 이유는 가장 최대 확률이 나올 것의 하한이 수식 2이기 때문이다. 하한을 보장하게 됨.
-
수식 3 복원오차
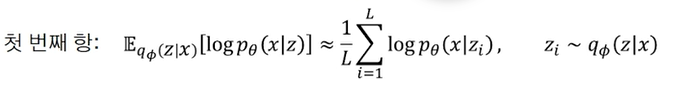
-
수식 3은 첫번째 항으로 이는, 잠재변수 z가 주어졌을 때, x의 분포를 알고 싶은것임.
즉, 인코더를 통한 잠재변수를 다시 디코더에 넣어 복원했을때, 원본 입력x와 동일하도록 하는 것. -
수식 4 정규화 항

-
수식 4는 2개의 분포를 가지고, 쿨백-라이블러의 발산을 계산하는 것으로, 표준정규분포를 가정하고 있기에 계산이 가능해진다. 평균과 분산을 통해 계산이 가능해짐.
VAE의 손실함수
- MLE(최대가능도)대신에 ELBO의 합을 최대화 해야함. "-(ELBO의 합을 최소화)"를 의미함.
- 손실 함수 계산 시 샘플링이 필요하다는 것 -> 미분 불가능함.
2. 재매개변수화 방법
- 정규 분포의 특성에서, 표준편차를 곱하고 평균을 더한 분포는 정규분포가 같다는 특성을 이용한다.
변분 오토 인코더의 활용
VAE는 생성과정은
- 잠재벡터(z)를 표준정규분포에서 샘플링.
- 디코더의 분포 p(x|z)로부터 새로운 데이터를 생성함.
이미지는 뿌옇지만, 데이터의 특징은 잘 잡고서 생성이 가능하다.
1. B-VAE

- 잠재벡터에 강한 정규화로 각 차원 별로 독립적인 정보를 가지도록 학습하여, 의미가 있는 잠재표현을 학습할 수 있으므로, 데이터의 특징을 잘 담게 된다는 특성이 있다.
2. VAE 장점
- 데이터를 요약하는 유용한 잠재 표현을 찾을 수 있다.
3. VAE 단점
- 가능도가 아닌 가능도의 하한을 최대화 한다는 것.
- 흐릿한 이미지를 생성한다는 점.
VQVAE - 벡터양자화 변분 오토인코더
-
잠재벡터가 이산(Discrete)인 벡터 양자화 VAE
-
실제 이미지나 텍스트는 유한한 특성으로 표현할 수 있음.
-
기존의 표준정규분포인 z(잠재벡터)에서 K개(특성의 강도를 나타내는 K개)의 D차원 임베딩 벡터로 매핑(mapping)함.
-
예시)
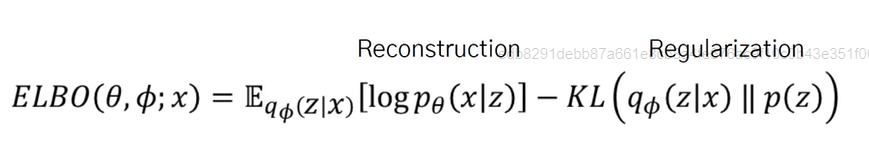
1. 복원 오차(첫번째 항)
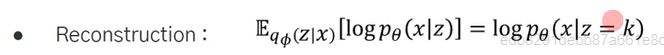
기존 VAE와 마찬가지로 입력/출력이 동일해야 함.
2. 규제화
-
앞서 기존은 z가 정규분포를 따른다고 하였지만, K(특성의 강도를 표현함)개를 Uniform 벡터(특성을 고정된 수의 Uniform 벡터)로 표현된다면 사전 분포 p(z) = 1 / K
-
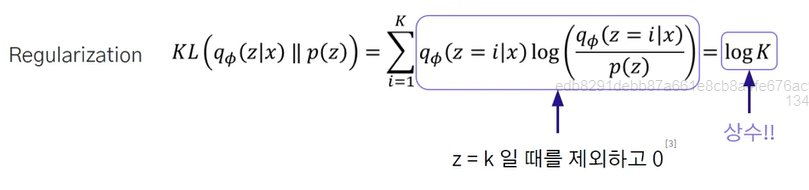
위 처럼 변경된 것을 볼 수 있음. 기존의 정규화가 log (K)가 되므로 상수로 되어, 두번째 항은 제거할 수 있게 됨.
3. VQVAE의 학습
- K개의 임베딩 벡터로 학습하게 함.
- 손실함수 (하나의 데이터로의 표현으로, sum, batch표현은 생략)
1. K개의 임베딩
수식 1

인코더의 출력 벡터가 입력의 특징을 추출한 정보를 담은 것으로 파란 박스를 의미한다.
하지만, 박스 부분을 통한 학습만 이루어질 경우, 인코더는 무한한 임베딩 공간으로 mapping을 진행기에 임베딩 공간에 입력이 흩뿌려질 수 있다는 단점을 가지고 있음.
수식 2

따라서, 약속 손실로 기존 인코더의 출력이 너무 커지지 않도록 임베딩 벡터 근처로 가까워지게 loss를 가하게 됨.
- sg = stop gradient - backpropagation시 입력에 대한 기울기를 0으로 계산함.
- > 0으로 하이퍼 파라미터
2. 미분 불가능
- 잠개변수 (x) = 디코더의 입력은 인코더 출력((x))에 대해 미분 불가능함.
- 이를 잠재 변수에 대한 기울기를 인코더 출력에 전달하여(인코더의 출력을 디코더의 기울기에 복사해서 학습함) 미분 가능하도록 전환하였음.
4. 생성과정
- 잠재변수 4x4개, 임베딩 벡터 512개
- 가능한 잠재 변수의 가짓수 : 엄청 커지게 됨.
- 관측치 개수 만큼의 잠재 변수의 조합만 확인가능하도록 하여 단순 사전 분포에서 샘플링은 의미가 없음.
즉 새로운 샘플을 생성하기 위해서 랜덤한 uniform 벡터를 가져와 디코딩을 진행함. 여기서의 문제가 실제에서의 분포가 랜덤한 uniform분포가 아니라는 점에 있다. 즉 의미가 없는 분포를 가져와서 디코딩에 넣게 된다는 점에 있다. 이를 해결하기 위해 잠재변수의 조합을 PixelCNN으로 학습하여 샘플링하는 방법을 도입하게 됨.
4.1 PixelCNN
- PixelCNN
이미지 픽셀 값(0~255)들의 결합 분포를 Masked 합성곱 신경망으로 모델링 한 것.
좌상단에서부터 순차적으로 이미지의 픽셀값을 생성함. 순서 : <왼->오른쪽 // R - G - B >
VQVAE-2
- 고해상도 이미지를 다루기 위한 계측 구조를 사용한 VQVAE임.
- 계층 구조
위(Top level) : 전역적인 Global 특징 - 배경, 거친 배경
아래(Bottom level) : 국소적인 Local 특징 - 아직 세부적인 디테일 까지는 아니지만, 부리, 털의 모양, 날개의 깃털
