upStageAI/패캠(기술통계)

TOLL TERRY·2023년 10월 14일

업스테이지AI_패스트캠퍼스

upstageAI_패스트캠퍼스

목록 보기

2/20

2일차 얘기 시작.

https://github.com/wakexmango/wakexmango

패스트캠퍼스[나의 커리어 치트키 데이터 분석 유치원]-챕터4_통계 실험과 유의성 검정

1. 가설 검정

내가 세운 가설이 통계적으로 유의미한 것임을 확인하는 것
순서 ##

귀무가설과 대립가설을 설정한다.
p-value를 구하고, p-value를 기준으로 가설 채택/기각을 결정

귀무가설 (Null)

지금까지 널리 알려져 있는 주장.
보수적인 가설
귀무가설은 기각이 우리의 목표

대립가설(Alternative)

연구자가 주장하고싶은 새로운 가설
대립가설은 채택이 목표임.

< p-value >

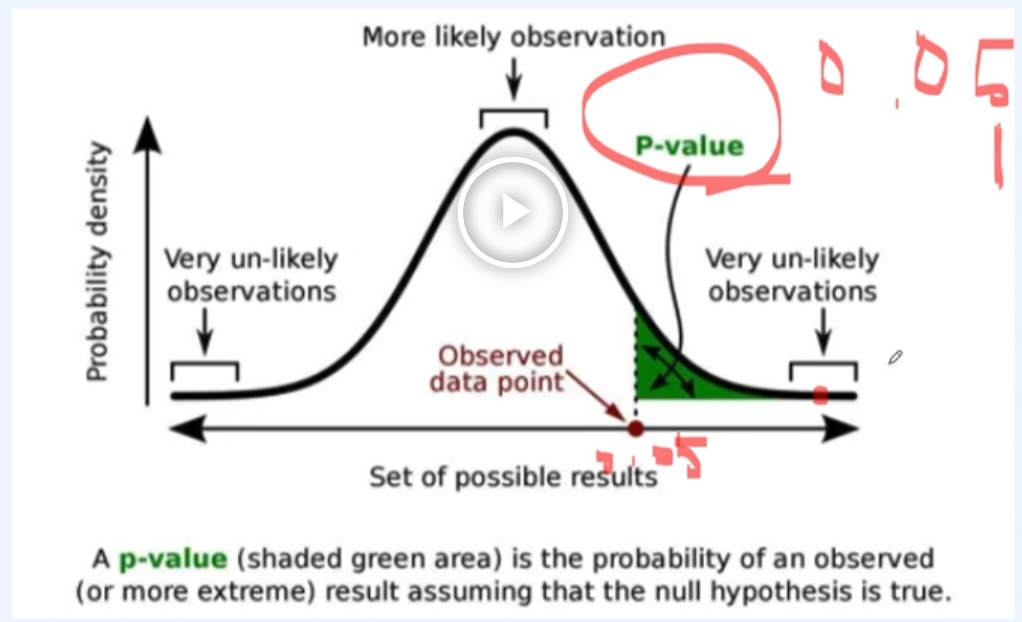
출처 : https://www.simplypsychology.org/

p-value가 0.05의 값을 기준이라면,
데이터의 분석을 통해서 p-value의 값이 만약 0.001이 나오게 된다면, 귀무가설이 일어날 일이 현저히 적기 때문에, 귀무가설을 기각하고서, 대립가설을 채택한다.

2. 단축검정(one-tailed)과 양측검정(two-tailed)

방향성을 기준으로 단축(한 방향), 양측(방향성은 모르지만 차이가 있을 경우)

단축검정

한 방향성으로 가능성이 클때,(30대의 재력이 20대의 재력보다 많을 것이다.

양측검정

방향성은 모르지만, 차이가 있을 경우,(30대가 다른 연령대의 재력과 차이가 있나?)

3. 검정에서의 1종 오류와 2종 오류

1종 오류 - FP - 재현율

귀무가설이 옳은데도 이를 기각 : 암이 아닌데 암이 발병했다고 진단한 경우

2종 오류(1종 보다 더 심각한 오류) - FN - 민감도

귀무가설이 옳지 않은데 이를 채택 : 암이 발병했는데, 암이 아니라고 진단한 경우

4. t-검정

모집단을 대표하는 표본으로부터 추정된 분산(표준편차)를 가지고
두 모집단의 평균간의 차이는 없다 - 귀무가설,
두 모집단이 평균 간에 차이가 있다 - 대립가설 둘중 하나를 선택하는 검정
t-value = 표준오차 / 표본 평균 사이의 차이(두 집단의 평균)

등분산성 가정

p-value를 확인 (levene 파이썬 라이브러리)
분산이 서로 같다. 귀무가설
분산이 서로 다르다. 대립가설
등분산성에 따라서는 p-value를 확인하면서 0.05보다 크면 귀무가설이 채택될 수 있다.

5. 분산분석(ANOVA) - 카이제곱, F분포 등

분산분석(ANOVA) 후 사후분석을 한다.

3개 이상의 다수 집단을 비교할 때 사용하는 검정 방법

F분포 = 집단 간 분산 / 집단 내 분산

등분산성의 가정 => 집단 내 분산이 서로 비슷한가? (비슷해야 비교가 가능)

일원 분석(one-way) - 순서대로 진행한다. F분포

정규성 검정
정규분포를 따르는 지 확인하기 (shapiro 파이썬 라이브러리) p-value가 0.05보다 커야함.
등분산성 검정
분산이 비슷한지 확인하기 (leven 파이썬 라이브러리) p-value가 0.05보다 커야함.
최종
일원 분산은 stats.f_oneway(집단3개) - p-value가 0.05보다 적다면 대립가설이 채택됨(우리가 새롭게 주장한 것, 집단 3개가 서로 차이가 있다.)
사후 분석(post-hoc)
paiwise_tukeyhsd(집단의 value, 집단) 파이썬 라이브러리
p-adj(=p-value)이므로 0.05보다 작아야 우리의 대립가설이 채택이 유의미한 것.

일원 분석(one-way) - 순서대로 진행한다. 카이제곱분포

A/B테스트에 활용됨

귀무가설 : 유저a와 유저b가 c페이지에 진입하는 것이 관련이 없다.
대립가설 : 유저a와 유저b가 c페이지에 진입하는 것이 관련있다.

표를 작성해야하고
왼쪽 열이 유저들, 행이 페이지 진입하는지 안하는 지

독립성 검정 : 두 변수가 서로 연관성 있는 지
적합성 검정 : 실제 표본이 내가 가정한 분포와 같은지
동일성 검정 : 두집단의 분포가 같은가

업스테이지 - 안창배 강사님 강의

round-off 문제
파이썬에서 0에 가까운 값을 더할때, 0.0000005 이런식으로 아주 작은 값을 더하는 문제들이 발생한다는 점이 있다.

1. 추정과 기대값

통계적 추론
추론의 이해
통계적 가설 검정

#통계적 추론

추론과 예측

추론 : 데이터를 이해. 데이터의 크기 작음, 데이터를 보고 이해가능성 큼, 미래를 추론이니 과거 데이터에 중점
예측 : 결과만 요구됨. 데이터의 크기 큼, 데이터를 보고 이해가능성 작음, 과거보다는 미래를 잘 맞추는 것에 중점

<통계적 가정>

잔차(모델의 나머지)에 특정한 패턴이 없다는 가정. ex) ANOVA 화이트 노이즈를 따라야한다.
어떤 분포를 따른다는 가정, 일관된 분포라는 가정
검정하려는 특성(평균)외에 다른 특성(분산)이 비슷하다는 가정
기타 등등

평균 비교(two-sample t-test)의 가정
- 이상치가 없음, 두 집단의 분산이 비슷하고, 집단 내의 각 관측치는 같은 분포, 순서에 영향이 없어야 한다.

<통계적 가정의 의미>

위의 가정이 맞지 않을 경우, 결과 신뢰할 수 없으며, 검사한 것들에서는 문제가 나오지 않았다 라고 얘기할 수 있으며, 가정이 강력할수록 그 결과에서만 정확한 추론이 가능함.

모수

각 분포의 특성을 결정짓는 수. ex) 정규 분포의 평균, 혹은 분산
t-test(평균)와 ANOVA(평균,분산) -> 모두 평균을 맞추는 것임.
선형회귀(Linear Regression) -> beta를 맞추는 것
k-means -> 평균과 분산을 추정함.
고전통계학은 모수(=고정된값임, H, 가설)로부터 데이터를 추정함. P(H|e) = P(e|H)
현대통계학은 데이터로부터 모수(H, 가설)를 추정함. 베이지안 P(H|e) = P(e|H) $*$ P(H) / P(e)

<베이지안> - 현대통계학
데이터를 가지고, 모수가 어떤것이라 가정하는 prior, 이를 통해 posterior를 업데이트 하는 방식.

e == Data(D)

P(e|H) = H(귀무가설)를 가정했을때, 데이터(e)가 나올 확률
최대 Likelihood = 무한하게 많은 H(가설)중에 데이터를 가장 잘 설명하는 가설을 뽑는 것

A/B테스트 - hackle ab test(베이지안통계), 쿠팡 플랫폼

#추론의 이해

추정량 (확률변수임)

모수에 대한 예측
실제 데이터로부터 많은 값은 추정치로 분리함.
편향이 없을 경우 좋음.
분산이 낮은 경우 좋음.
데이터가 무한하게 커질때, 추정이 수렴(극한으로)할 경우 좋음.

<편향-분산>

LASSO는 (=L1 정규화 마름모모양임)(여기서 L2는 유클라디안 원모양)약간의 편향을 허락하며, 분산을 줄임으로 더 적은 오차를 달성하는 모델
편향과 분산은 trade-off임.

<구간 추정과 p-value>

데이터를 확인한다면, p-value을 기준으로 가설을 기각과 채택을 설정함.
신뢰수준 (허용 가능한 오차, 오차를 타협해야함) - 모수가 신뢰구간 안에 들어갈 확률이 95%이다.
신뢰구간 (표본을 뽑아 신뢰 구간을 무수히 많이 계산시, 100번 중 95번은 신뢰구간이 모수를 포함하고 있다.)

< MLE >
데이터로부터 모수를 추정하는 것
; = given 주어지는 것

< Likelihood >

개념 - 데이터로부터 모수를 구한다는 현대통계학.
$L$ (θ ; $x1, x2, ..., xn$ ) 오른쪽이 데이터
수식 - 모수로부터 데이터가 나올 확률이라는 고전 통계학임.
$f($ x1, x2, ..., xn$ ; θ) 오른쪽이 모수

가능도 함수, 관측된 데이터를 고정한 상태에서 세타를 변수로 생각한다. 우도를 최대화 하는 세타를 찾는 것이 목표임. 상황이 독립이라 모두 곱함.

< 최대 Likelihood >

1차 미분을 이용한다.
Normalizer을 이용한다. 포아송에서는 e-λ, 정규 분포에서는 σ 표현 제외
λ 찾기 위해서는 log 변환, 상수제외,
참고 MLE 링크 : https://statproofbook.github.io/P/ug-mle.html

< 몬테카를로 MonteCarlo>

시뮬레이션을 많이 돌려보며, -1~1사이의 값을 2개 뽑아(x,y) 반지름 1인 원 안에 들어가는 지 검사하며, 원의 부피를 근사한다.

<부트스트랩>

재추출을 반복하여, 신뢰구간까지 구할 수 있는 MC(몬테카를로)기법
연산량이 많다는 단점이 있지만, 어디서나 쓰일 수 있다는 장점

#통계적 가설 검정

주어진 자료가 특정한 가설을 충분히 뒷받침 하는지 여부를 결정하는 통계적 추론 방법임.

오차에 제곱을 하는 이유 (MSE, RMSE)

제로가 되는 것을 (마이너스, 플러스) 방지하기 위해서
제곱을 통해, 모두 양수로 만들 수 있음, 이상치 제곱에 민감함
하지만, 제곱이 항상 정답이라 할 수 없음, 세제곱(복소수), MAPE(시계열)같은 방법도 있음

<T-test의 한계>

3개 이상의 집단에서는 검정이 불가능 --> 해결하기 위해 ANOVA
2개에서도 ANOVA를 사용하는 것과 T-test는 100% 동일함.( $x^2$ )
(하지만 One-tailed 단측에서는 ANOVA를 사용할 수 없음, 왜냐하면 T-test의 양측검정과 F검정의 단측검정이 동일하기 때문이다.)