3일차 이야기 시작.
패스트캠퍼스 [나의 커리어 치트키 데이터 분석 유치원] 파트3, 챕터 5 선형회귀분석
-
회귀
독립변수 x(영향을 미칠 변수)로 종속변수 y(영향을 받는 변수)를 예측하는 것
회귀계수 = 기울기와 절편 (a(기울기)x + b(절편)) -
다중선형회귀분석
-- 여러 독립변수가 존재 x1, x2, x3, ..., xn
-- 하나의 결과를 여러 원인으로 설명하기 위한 분석 방법
<결정계수>
-- 독립변수(x)가 종속변수(y)를 얼마만큼 설명해주는지 가리키는 지표
-- 독립변수가 종속변수의 50%정도를 설명하는 0.5 (일반적으로 20% = 0.2)
-- = -
선형회귀의 기본 5가지 검정
@ 오차 : 모집단에서 회귀식을 얻어 회귀식을 통해 얻은 예측값과 관측값의 차이>
@ 잔차 : 표본집단에서 회귀식을 얻어 회귀식을 통해 얻은 예측값과 관측값의 차이>
-- 선형성 : 선형적
-- 잔차 정규성 : 잔차는 정규분포를 이루어야 한다.
-- 독립성 : 다중 선형회귀에만 해당하는 가정, 독립변수(x)들은 모두 독립
-- 다중 공선성 : 다중 회귀분석을 수행할 경우, 독립변수 간에 강한 상관관계 아니어야 함. (=======> +-0.6이하가 되어야함. )
-- 등분산성 : 분산이 특정 패턴이 없이 일정해야 한다.
upstageAI 안창배 강사님 강의시작
1. ANOVA (분산분석)
-
SST (SStotal, SSTreatment)
-
SS_error = 집단내의 분산(개수가 많음 = k개)
-
SS_treatment = 집단간의 분산(개수가 적음)
-
MS_treatment = SS_treatment / (k-1) ... -1인 이유는 전체 평균에서 빼기에 자유도 1임
-
MS_error = SS_error / (n-k) ... 각 집단의 수 별 빼기에 k개 만큼을 뺀 것임.
-
F분포 = MStreatment / MSerror
F분포는 카이제곱 분산의 비율을 따름, 또한 여기서 모두 정규분포를 따른다는 가정이 요구.
가정검토
-
어떠한 패턴이 없다는 것을 확인하는 가정임. 우리는 패턴을 찾는 것이 목표인데, 패턴을 찾고서 남은 패턴이 없다는 것. 그렇기에 원본 데이터가 아닌 잔차에 대한 가정으로 이는 원본데이터가 정규분포를 따른다는 것은 아님을 의미한다.
-
정규성(왜도와 이상치에 문제가 발생, 잔차의 분포가 정규분포), kolmogorov(대용량), shapiro(3000개 이하 데이터일때), 수십만개(q-qplot, 1000개씩 샘플링)
-
독립성(각 관측치의 순서에는 패턴이 없다. 보통 시간 순서에 따라 데이터가 배치된 경우 문제가 발생(시계열)), DW test
-
등분산성(각 집단의 분산은 동일하다, 하지만 왜도 문제가 발생한다.), Bartlett's test
정규성, q-qplot
왜도와 이상치는 log변환이나 이상치 제거가 90%으로 이슈해결한다.
독립성
- bias(편향)에는 문제가 생기지 않으며, 비교적 문제가 치명적이지 않음.
- DW-검정 = 평균을 찍어서, 평균보다 큰것이 몇개있는 지 연속적으로 확인하는 검정, 잔차 residual에 대한 시계열 타임-시리즈 모델링(facebook prophet등)으로 해결한다.
등분산성
- 일분산(homo) vs 다분산(hetero)
- 각 집단의 분산이 동일하다는 가정
- 가정이 어긋나면 2종오류 (심각, fn, 민감도)에 위험이 증가한다.
- skew(왜도)를 잡기위해 log-변환 한다.
< welch-T-test >
- t-test에서도 이분산을 가정한 t-test을 사용함. 2개의 합동분산을 사용하여, 자유도를 새터스웨이트 자유도(Satterthwaite 자유도)의 변경이 발생한다. 이상치만 조심
< log 변환의 효과>
- 독립변수 x의 값에 따라 y의 값에 변동이 있다면, x값의 변화에 따라 y값의 분산이 달라지는 것은 굉장히 일반적이기에 log변환으로 잘 잡힐 수도 있다.
사후검정(Post-hoc)
- tucky
- bonferroni ---
등등을 보고서 사후검정을 하자.
2. 카이제곱 test의 독립성
- 카테고리의 Nominal
카이제곱 검정
- 독립성,
2개 이상의 범주형 자료가 서로 독립인지 확인 - 적합도,
하나의 범주에 대한 검사이기에, 단일/이중 표본 t검정의 차이와 유사하기에, - 동질성,
한 범주의 모집단이 분리되어, 성별이 5:5가 맞는지 확인하는 것
< 카이제곱 검정과 분할표 >
- [2 2]에서는 자유도 1 ------ [3 3]에서는 자유도 3
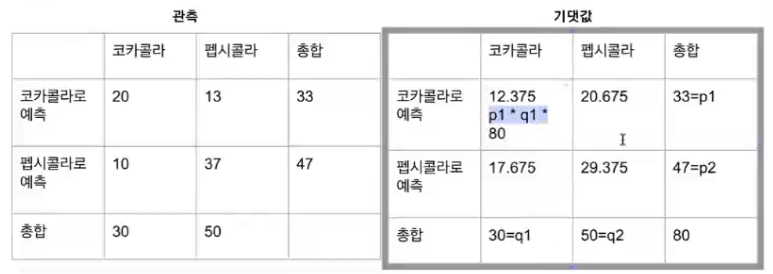
12.375 = (p1=33) * (q1=30) / 80
- 독립성 검정
귀무가설 : 각 범주는 독립이다.
대립가설 : 각 범주는 독립이 아니다.
독립성 검정에는 양극단 문제가 발생하므로, 이는 각cell은 최소 5이상을 권장
데이터가 적으면 fisher의 exact test : 초기하 분포 가정한다.
이항분포에서도 n p > 5, n q > 5이상일때, 정규 근사할 수 있도록 권장한다.
