[자료구조] 4. Tree

shiny_Silver·2023년 11월 10일
Cdata structure
0

Data Structure

목록 보기
4/7
post-thumbnail

4.1 트리란?

트리는 계층적 자료를 저장하는데 적합한 자료구조이다. 컴퓨터 디렉터리의 구조를 생각해보자. 상위 디렉터리는 여러 하위 디렉터리로 구성되어 있고, 하위 디렉터리는 또 여러 하위 디렉터리로 구성되게 된다. 여기서 우리가 눈치챌 수 있는 트리의 주요한 특성 중 하나는 트리는 재귀적(recursive)으로 구성되어 있다는 점이다. 트리의 개념에 대해 정확히 이해하기 위해선 몇가지 용어를 정리할 필요가 있다.

◼ 트리: 한 개 이상의 노드로 이루어진 유한 집합이다. 루트(root) 노드를 가지며 나머지 부분은 n개의 서로소 집합을 이루며 이를 서브 트리라고 한다.

◼ 루트(root) 노드, 리프(leaf) 노드: 루트 노드는 트리의 계층적 구조에서 가장 높은 곳에 있는 노드이고, 리프 노드는 더 이상 하위 노드가 존재하지 않는 가장 아래에 존재하는 노드를 지칭한다. 리프 노드는 단말(terminal) 노드라고도 한다.

◼ 노드 사이의 관계

부모, 자식 관계: 위 아래로 직접적으로 연결된 노드 사이의 관계. 위쪽의 노드가 부모 노드, 아래쪽이 자식 노드에 해당한다.

조상, 후손 관계: 특정 노드로부터 간선을 타고 내려가면서 만날 수 있는 모든 노드들을 해당 노드의 후손, 특정 노드로부터 간선을 타고 올라가면서 만날 수 있는 모든 노드들을 해당 노드의 조상 노드라고 한다.

형제 관계: 같은 부모 노드를 갖는 노드들 사이의 관계

◼ 깊이(depth): 루트 노드의 깊이를 0으로 설정하고 트리의 한 층씩 내려갈수록 1씩 증가한다.

◼ 차수(degree): 자식 노드의 수. 트리의 차수는 트리가 가진 노드의 차수의 최댓값이다. 리프 노드의 차수는 0이다.

◼ 높이(height): 가장 깊은 노드의 깊이가 트리의 높이가 된다.

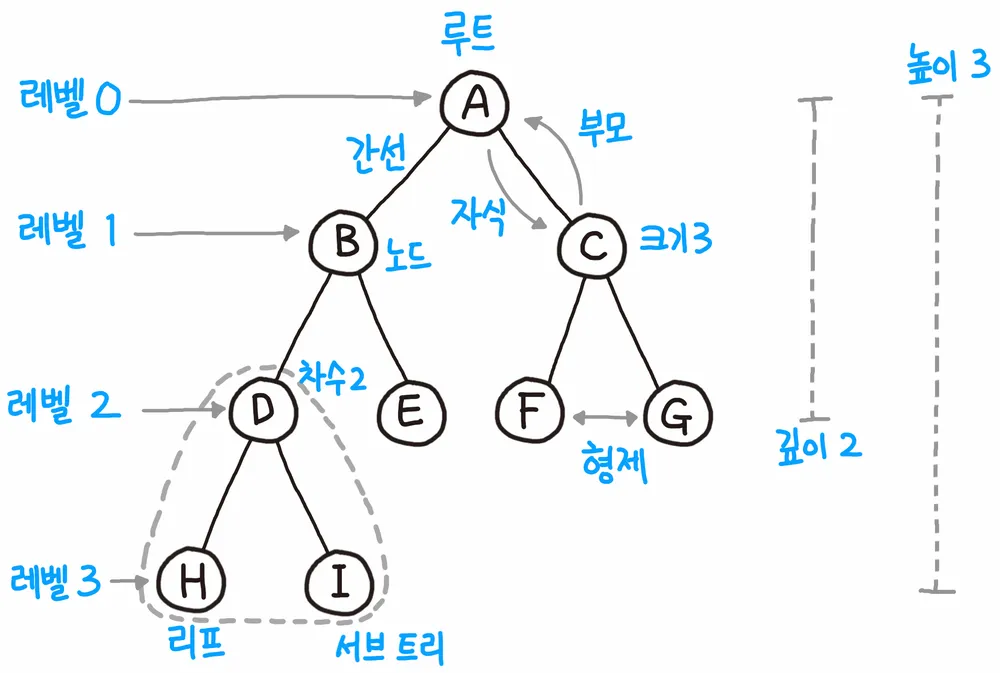
◼ 이진 트리(binary tree): 이진 트리는 공집합이거나 루트와 2개의 서브 트리로 구성된 유한 집합이다. 또한 두 개의 서브 트리가 왼쪽 서브 트리, 오른쪽 서브 트리로 구별된다. 이진 트리는 재귀적으로 정의되며, 이는 이진 알고리즘을 작성하는데 매우 중요하게 작용한다.

4.2 이진 트리

4.1.1 이진 트리 분류 및 특성

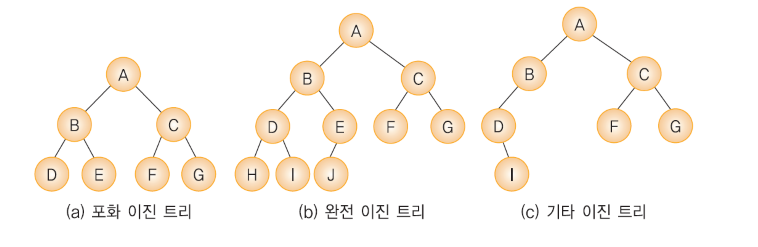
이진 트리는 그 형태에 따라 포화 이진 트리(full bianary tree), 완전 이진 트리(complete binary tree)와
그 외 일반적인 이진 트리로 구별할 수 있다.

◼ 포화 이진 트리

포화 이진 트리는 그림과 같이 모든 깊이에 노드가 꽉 차있는 형태이다.
포화 이진 트리가 n개의 노드를 갖고 그 높이가 h라고 가정하자.
총 노드의 수는 20+21+22+⋯+2h2^0+2^1+2^2+⋯+2^h으로 나타낼 수 있고, n=2h+1−1n=2^{h+1}-1이다.

이때 평균 비교 횟수를 계산해보자. root노드에서 비교 횟수가 1이므로 각 노드에서 비교 횟수는 (깊이+1)이라는 것을 알 수 있다.

총 비교 횟수: SS, 평균 비교 횟수: SnS\over n

S=(1×20)+(2×21)+⋯+((h+1)×2h)2S=    (1×21)+⋯+(h×2h)+((h+1)×2h+1)\begin{aligned} S&=(1\times2^0)+(2\times2^1)+⋯+((h+1)\times2^h)\\ 2S&=\quad\quad\quad\quad\;\;(1\times2^1)+⋯+(h\times2^h)+((h+1)\times2^{h+1}) \end{aligned}
∴S=−(20+21+22+⋯+2h)+(h+1)×2h+1=h×2h+1+1=h(2h+1−1)+h+1\begin{aligned} ∴S&=-(2^0+2^1+2^2+⋯+2^h)+(h+1)\times2^{h+1}\\ &=h\times2^{h+1}+1\\ &=h(2^{h+1}-1)+h+1 \end{aligned}
∴Sn=h(2h+1−1)+h+1n=h+h+1n=log⁡2(n+12)+log⁡2(n+1)n\begin{aligned} ∴ \frac{S}{n}&=\frac{h(2^{h+1}-1)+h+1}{n}\\ &=h+\frac{h+1}{n}\\ &=\log_{2}{(\frac{n+1}{2})}+\frac{\log_{2}{(n+1)}}{n} \end{aligned}

◼ 완전 이진 트리

완전 이진 트리는 높이가 h일때, 높이 h-1까지는 노드가 모두 채워져 있고 마지막 레벨 h에서는 왼쪽에서 오른쪽으로 순서대로 노드가 채워져있는 이진 트리이다.

◼ 이진 트리의 특성

  • n개의 노드를 가진 이진 트리의 간선의 수는 n-1개이다.
  • n개의 노드를 가진 이진 트리의 extended binary tree의 external 노드의 수는 n+1개이다.
    (extended binary tree는 NULL을 모두 표시한 트리로 external 노드(NULL)는 ◻, internal 노드는 ◯로 표기)
  • recursion call이 2회 일어나는 경우, recursion 트리의 모양은 원래 이진 트리의 extended 모양이다.
    (이후에 살펴 볼 이진 트리의 height와 size를 구하는 경우가 해당 됨)

4.2.2 이진 트리 순회

순회는 이진 트리에 속하는 모든 노드들을 한 번씩 방문해 노드에 저장된 데이터를 확인하는 것을 말한다. 순회는 가장 기본적인 연산으로서 다른 연산을 구현하기 위해 필수적으로 선행되어야 한다. 예를 들어 search 연산을 수행하기 위해선 노드들을 방문해 입력된 값과 비교해 일치하면 출력, 일치하지 않으면 순회를 이어나간다. add나 delete 연산도 마찬가지이다.

앞서 다뤘던 배열, 스택, 큐, 연결 리스트 같은 선형 자료 구조와 다르게 이진 트리는 계층적 자료 구조이므로 순회 방법을 여러가지로 생각해볼 수 있다. 3가지 순회 방법을 알아보고 pseudo 코드로 구현해보자.

1. preorder traversal (VLR)

Visit the root
-> Traverse the Left subtree in preorder
-> Traverse the Right subtree in preorder

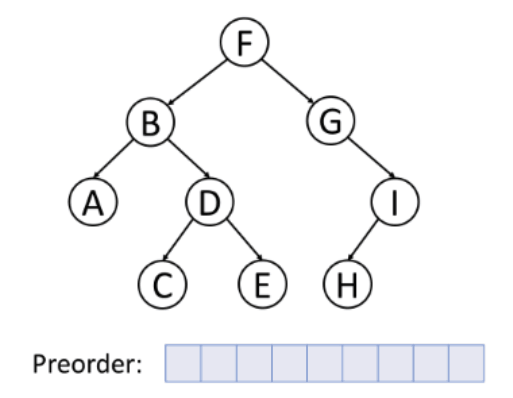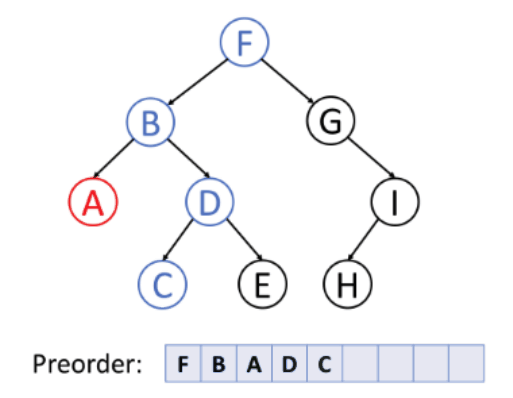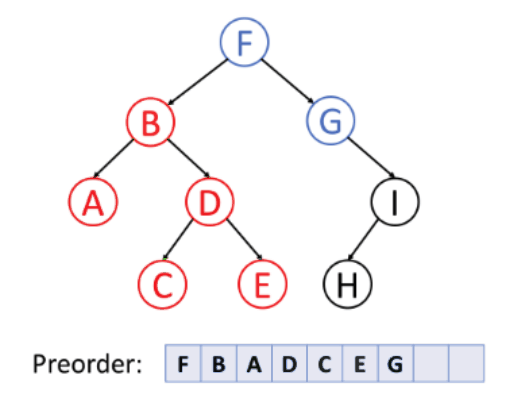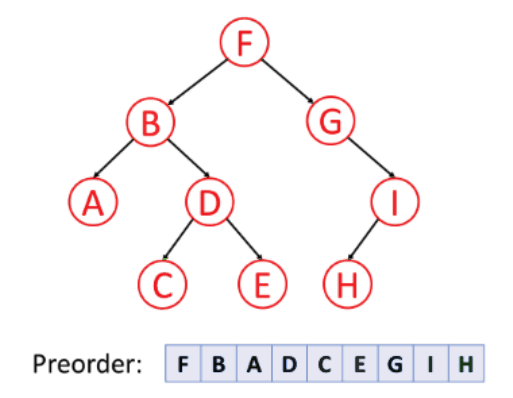
preorder(root):
	if(root!=NULL)
    	then print(root->data);
        	 preorder(root->left);
        	 preorder(root->right);

이진 트리는 재귀적으로 구성되어 있으므로 재귀적인 function call을 통해 연산을 구현하는 것이 자연스럽고 이해하기 쉽다. 하지만 재귀적 방법의 단점도 존재하므로 반복적인 방법을 통해서도 구현해보도록 하겠다.

2. inorder traversal (LVR)

Traverse the Left subtree in inorder
-> Visit the root
-> Traverse the Right subtree in inorder

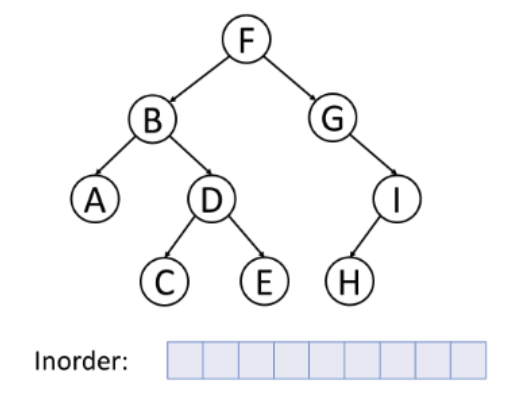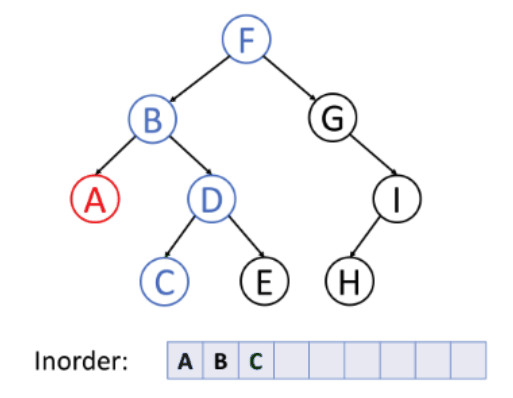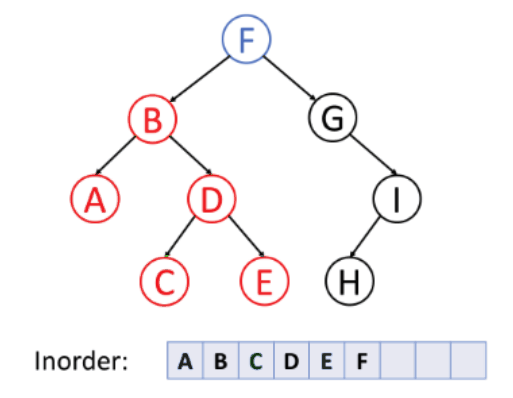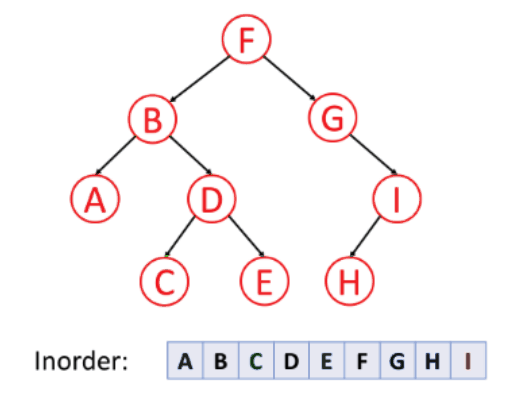
inorder(root):
	if(root!=NULL)
    	then inorder(root->left);
    		 print(root->data);
        	 inorder(root->right);

3. postorder traversal (LRV)

Traverse the Left subtree in postorder
-> Traverse the Right subtree in postorder
-> Visit the root

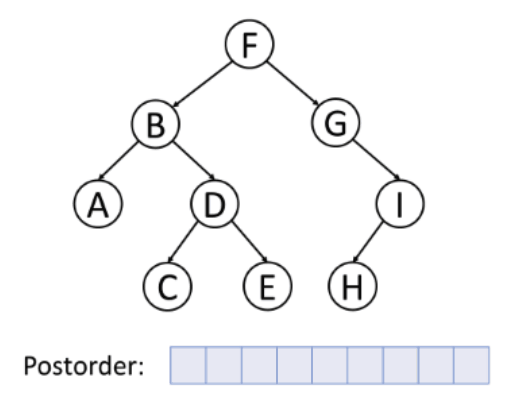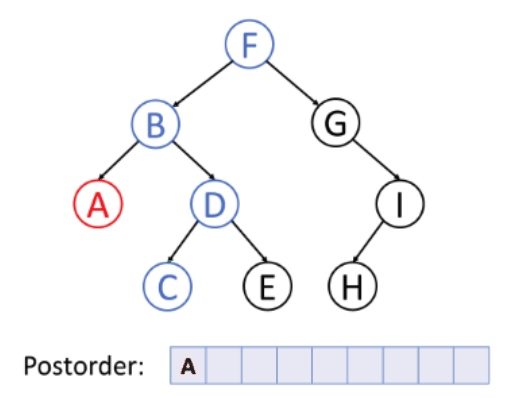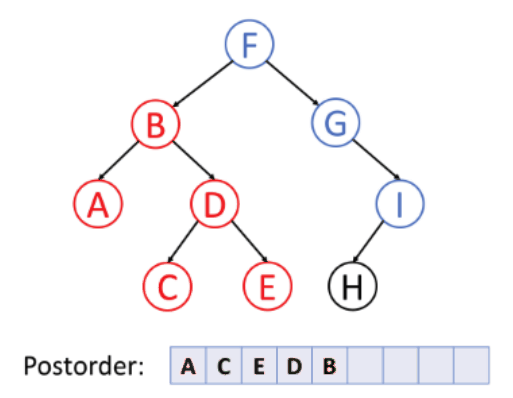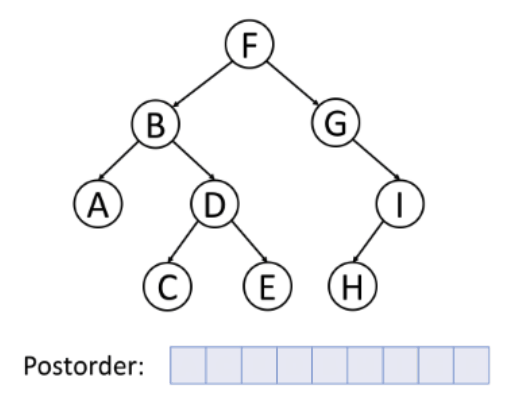
postorder(root):
	if(root!=NULL)
    	then postorder(root->left);
    		 postorder(root->right);
        	 print(root->data);

4.2.3 재귀적 순회 구현

// Recursive vesion of Traversing

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode{
    char data;
    struct TreeNode *left, *right;
} TreeNode;

TreeNode n9 = {'I', NULL, NULL};
TreeNode n8 = {'H', NULL, NULL};
TreeNode n7 = {'G', NULL, NULL};
TreeNode n6 = {'F', &n8, &n9};
TreeNode n5 = {'E', NULL, &n7};
TreeNode n4 = {'D', NULL, NULL};
TreeNode n3 = {'C', &n5, &n6};
TreeNode n2 = {'B', &n4, NULL};
TreeNode n1 = {'A', &n2, &n3};
TreeNode *root = &n1;

// 정적인 트리의 구조
//        A
//    B       C
//  D  ◻    E   F
// ◻ ◻     ◻ G H I

// Traverse in preorder: VLR
// Visit root -> Left subtree -> Right subtree
// A B D C E G F H I 
void preorder(TreeNode *root){
    if(root != NULL){
        printf("%c ", root->data);  // root 데이터 출력
        preorder(root->left);       // 왼쪽 서브트리 순환 호출
        preorder(root->right);      // 오른쪽 서브트리 순환 호출
    }
}

// Traverse in inorder: LVR
// Left subtree -> Visit root -> Right subtree
// D B A E G C H F I 
void inorder(TreeNode *root){
    if(root != NULL){
        inorder(root->left);        // 왼쪽 서브트리 순환 호출
        printf("%c ", root->data);  // root 데이터 출력
        inorder(root->right);       // 오른쪽 서브트리 순환 호출
    }   
}

// Traverse in postorder: LRV
// Left subtree -> Right subtree -> Visit root
// D B G E H I F C A
void postorder(TreeNode *root){
    if(root != NULL){
        postorder(root->left);      // 왼쪽 서브트리 순환 호출
        postorder(root->right);     // 오른쪽 서브트리 순환 호출
        printf("%c ", root->data);  // root 데이터 출력
    }   
}

int main(){
    printf("[Recursive Ver]\n");
    printf("pre : "); preorder(root);
    printf("\n");
    printf("in  : "); inorder(root);
    printf("\n");
    printf("post: "); postorder(root);
}
-실행결과-

[Recursive Ver]
pre : A B D C E G F H I 
in  : D B A E G C H F I 
post: D B G E H I F C A

4.2.4 반복적 순회 구현

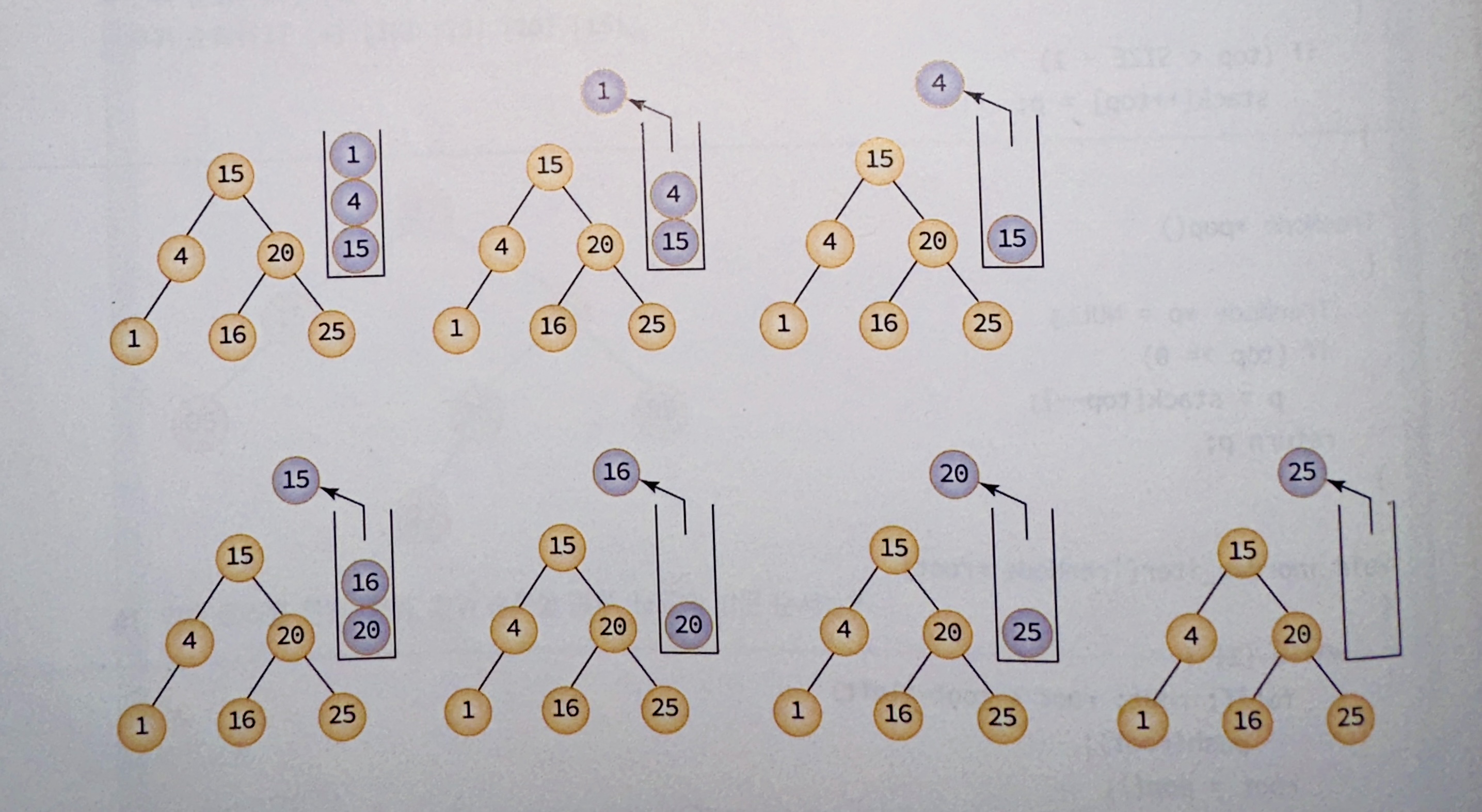
반복적 inorder 순회의 작동 흐름
반복적인 방법은 스택에 노드를 push, pop하며 순회를 진행한다.
반복적인 방법은 흐름이 헷갈릴 수 있으니 그림으로 이해해보자.

// Iterative version of Traversing

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode{
    char data;
    struct TreeNode *left, *right;
} TreeNode;

TreeNode n9 = {'I', NULL, NULL};
TreeNode n8 = {'H', NULL, NULL};
TreeNode n7 = {'G', NULL, NULL};
TreeNode n6 = {'F', &n8, &n9};
TreeNode n5 = {'E', NULL, &n7};
TreeNode n4 = {'D', NULL, NULL};
TreeNode n3 = {'C', &n5, &n6};
TreeNode n2 = {'B', &n4, NULL};
TreeNode n1 = {'A', &n2, &n3};
TreeNode *root = &n1;

// 정적인 트리의 구조
//        A
//    B       C
//  D  ◻    E   F
// ◻ ◻     ◻ G H I

#define SIZE 100
int top = -1;
TreeNode *stack[SIZE];

void push(TreeNode *p){
    if(top < SIZE - 1)
        stack[++top] = p;
}

TreeNode* pop(){
    TreeNode *p = NULL;
    if(top>=0)
        p = stack[top--];
    return p;
}
// 스택 top에 저장된 노드를 반환하고 top 한 칸 내림

void preorder_iter(TreeNode *root){
	TreeNode *node = root;

    while(top>=0 || node!=NULL){
        if(node!=NULL){
            push(node);
            printf("%c ", node->data);
            node = node->left;
        }
        else{
            node = pop();
            node = node->right;
        }
    }
}
// VLR
// 우선 root노드를 스택에 추가 및 출력
// node가 NULL에 도달할 때까지 왼쪽 자식을 스택에 추가함과 동시에 출력
// node가 NULL이면, node에 스택 top의 노드를 할당하고 node를 오른쪽 서브 트리로 이동
// 간단히 현재 노드가 NULL이면 상위 노드로 이동한 후 다시 오른쪽 서브 트리로 이동 해 preorder 반복

void inorder_iter(TreeNode *root){
	TreeNode *node = root;

    while(top>=0 || node!=NULL){
        if(node!=NULL){
            push(node);
            node = node->left;
        }
        else{
            node = pop();
            printf("%c ", node->data);
            node = node->right;
        }
    }
}
// LVR
// 우선 root노드를 스택에 추가
// node가 NULL에 도달할 때까지 왼쪽 자식을 스택에 추가
// node가 NULL이면, node에 스택 top의 노드를 할당하고 출력 후 node를 오른쪽 서브 트리로 이동
// 간단히 현재 노드가 NULL이면 상위 노드로 이동해 출력 후 오른쪽 서브 트리로 이동 해 inorder 반복

void postorder_iter(TreeNode *root){
	TreeNode *node = root;
    TreeNode *result[SIZE];
    int i = -1, j;

    push(node);
    while(top>=0){
        node = pop();
        result[++i] = node;
        if(node->left!=NULL)    push(node->left);
        if(node->right!=NULL)   push(node->right);
    }
    
    for(j=i; j>=0; j--){
        printf("%c ", result[j]->data);
    }
}
// LRV
// 우선 root노드를 스택에 추가
// node에 스택 top의 노드를 할당하고, node를 result 배열에 저장
// node의 왼쪽 자식, 오른쪽 자식 순으로 스택에 추가
// 스택이 빌 때까지 반복 후 result 배열에 저장된 값 역순으로 출력
-실행결과-

[Iterative Ver]
pre : A B D C E G F H I 
in  : D B A E G C H F I 
post: D B G E H I F C A

4.3 BST

4.3.1 BST란?

이진 탐색 트리(binary search tree)는 이진 트리 기반의 탐색을 위한 자료 구조이다. BST는 탐색을 효율적으로 하기 위해 몇 가지 규칙에 따라 생성된다. 우선 트리가 중복되는 값을 가질 수 있다고 가정하자.

  • 왼쪽 서브 트리의 키 값은 루트의 키 값 이하이다.
  • 오른쪽 서브 트리의 키 값은 루트의 키 값 초과이다.
  • 왼쪽, 오른쪽 서브 트리 또한 BST이다.(재귀적 특성을 가짐)

이러한 특성을 통해 찾고자 하는 값이 주어졌을 때 트리 전체를 순회하는 것이 아닌 루트의 키 값과 크기 비교를 통해 빠르게 탐색을 진행할 수 있다.

BST의 연산은 크게 search, insert, delete가 있으며, 재귀적 방법을 통해 구현해보려고 한다. 추가적으로 BST의 height와 size를 구하는 함수도 구현해보자.

먼저 insert, delete의 동작 흐름에 대해 알아보자.

◼ insert의 경우 우선적으로 탐색이 이루어져야 한다. 값 비교를 통해 삽입 위치를 탐색하게 되고 NULL 값을 만나게 되면 그 자리에 새로운 노드를 이어주면 삽입이 가능하다.

◼ delete의 경우는 Case를 나누어 생각해야한다.

  • Case 1: 삭제 노드가 단말 노드인 경우
    가장 간단한 경우로 부모 노드의 링크 필드를 NULL 값으로 만들고, 삭제 노드에 할당되었던 동적 메모리를 해제하면 된다.
  • Case 2: 삭제 노드가 하나의 서브 트리만 가지는 경우
    삭제 노드가 왼쪽 혹은 오르쪽 서브 트리만 가지는 경우이다. 이 경우도 간단히 생각할 수 있다. 부모 노드의 링크를 삭제 노드의 서브 트리를 가리키도록 변경해주고 삭제 노드에 할당된 동적 메모리를 해제한다.
  • Case 3: 삭제 노드가 두 개의 서브 트리를 가지는 경우
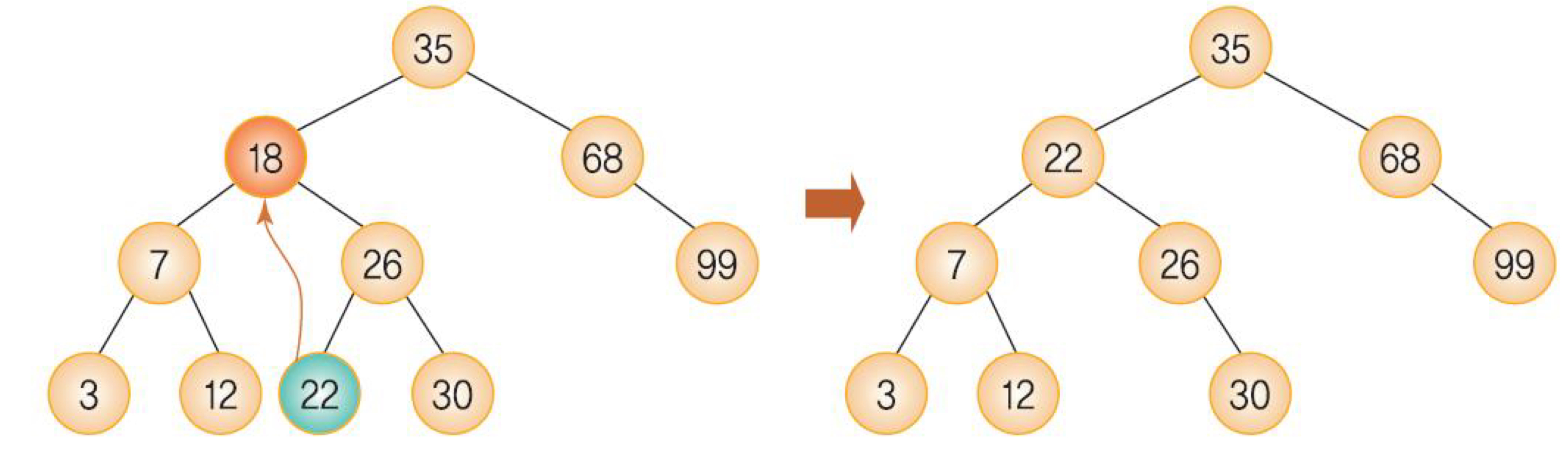
    가장 복잡한 경우로 생각할 요소가 많다. 노드를 삭제하여도 BST의 특성을 똑같이 유지하여야 한다는 것에 유의하여 생각해보자. 만약 왼쪽 자식이나 오른쪽 자식을 그대로 연결한다면 다른 노드들의 위치를 변경해주어야 BST의 특성을 유지시킬 수 있다. 다른 노드들을 변경시키지 않고 BST의 특성을 유지시킬 수 있는 적당한 노드를 찾아보자. 우리는 앞서 inorder 순회 방법에 대해 알아보았고, BST를 inoder로 순회한다면 크기 순으로 나열된다는 것을 확인할 수 있다. 그렇다면 이때 삭제 노드를 어느 노드로 대체하는 것이 자연스럽나? 바로 크기 순으로 나열하였을 때 삭제 노드의 키 값의 앞 뒤에 있는 노드일 것이다.(BST는 크기 순으로 트리가 생성되므로 비슷한 키 값의 노드로 대체한다면 트리의 구조를 변경시키지 않고 특성을 유지하는 것이 가능하다.) 이 노드들은 '왼쪽 서브 트리에서 가장 큰 값', '오른쪽 서브 트리에서 가장 작은 값'을 가지는 노드이며 각각 'predecessor', 'successor'라고 한다. 우리는 successor로 삭제 노드를 대체하는 코드를 작성할 것이다.
    정리하면 삭제 노드가 두 서브 트리를 가진다면 해당 노드의 successor를 찾아 키 값을 대체하고 삭제하면 된다.

    successor는 왼쪽 자식을 가질 수 없다.
    predeccessor는 오른쪽 자식을 가질 수 없다.
    successor 삭제 시, 오른쪽 서브 트리의 존재 여부를 고려해야 한다.

4.3.2 BST 재귀적 구현

// Recursive vesion of BST

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode{
    int data;
    struct TreeNode *left, *right;
} TreeNode;

TreeNode* search(TreeNode *node, int key){
    if(node == NULL) return NULL;
    
    if(key == node->data) return node;	// 키 값 일치하면 반환
    else if(key < node->data)			// 키 값이 작으면 왼쪽 서브 트리 search
        return search(node->left, key);
    else								// 키 값이 크면 오른쪽 서브 트리 search
        return search(node->right, key);
}

// 노드 할당 함수
TreeNode* new_node(int item){
    TreeNode *tmp = (TreeNode*)malloc(sizeof(TreeNode));
    tmp->data = item;
    tmp->left = tmp->right = NULL;
    return tmp;
}

// 삽입 함수
TreeNode* insert(TreeNode *node, int key){
    // 트리가 공백이면 새로운 노드 반환
    if(node == NULL) return new_node(key);

    if(key <= node->data)
        node->left = insert(node->left, key);
    else
        node->right = insert(node->right, key);

    // 변경된 트리의 root를 반환
    return node;
}

// 삭제 함수
TreeNode* delete(TreeNode *root, int key){
    if(root == NULL) return NULL;

    if(key < root->data) 
        root->left = delete(root->left, key);
    else if(key > root->data)
        root->right = delete(root->right, key);
    // key == root->data
    else{
        // Case 1,2: 삭제 노드가 단말 노드이거나 하나의 서브 트리만 갖는 경우
        if(root->left == NULL){
            TreeNode *tmp = root->right;
            free(root);
            return tmp;
        }
        else if(root->right == NULL){
            TreeNode *tmp = root->left;
            free(root);
            return tmp;
        }
        
        // Case 3: 삭제 노드가 양쪽의 서브 트리를 갖는 경우
        // 오른쪽 서브 트리의 최솟값으로 대체
        
        // tmp가 successor를 가리키도록 함
        TreeNode *tmp = root->right;
        while(tmp->left != NULL){
            tmp = tmp->left;
        }
        // 삭제 노드에 tmp 키 값 복사
        root->data = tmp->data;
        // successor 노드 삭제
        root->right = delete(root->right, tmp->data);
    }
    // 변경된 트리의 root 반환
    return root;
}

void inorder(TreeNode *root){
    if(root != NULL){
        inorder(root->left);        // 왼쪽 서브트리 순환 호출
        printf("%d ", root->data);  // root 데이터 출력
        inorder(root->right);       // 오른쪽 서브트리 순환 호출
    }
}

// BST 높이 계산 함수
int height(TreeNode *root){
    // root 노드만 존재하는 경우 height=0 이므로 초기값 -1로 설정
    if(root==NULL) return -1;

    int l = height(root->left);
    int r = height(root->right);
  
    // (BST의 높이) = (1 + 왼쪽, 오른쪽 서브 트리 중 height가 더 큰 값)
    if(l>r) return l+1;
    else return r+1;
}

// BST 노드 수 계산 함수
int size(TreeNode *root){
    // 초기값 0
    if(root == NULL) return 0;
    // (총 노드의 수) = (1 + 왼쪽 서브 트리 노드 수 + 오른쪽 서브 트리 노드 수)
    return 1+size(root->left)+size(root->right);
}

int main(){
    TreeNode *root = NULL;

    root = insert(root, 30);
    root = insert(root, 20);
    root = insert(root, 10);
    root = insert(root, 60);
    root = insert(root, 40);
    root = insert(root, 50);
    root = insert(root, 70);

    inorder(root); printf("\n");
    printf("height: %d size: %d\n", height(root), size(root));
    delete(root, 30);
    inorder(root); printf("\n");
    printf("height: %d size: %d\n", height(root), size(root));
    
    return 0;
}
-실행결과-

10 20 30 40 50 60 70 
height: 3 size: 7
10 20 40 50 60 70 
height: 2 size: 6
profile
shiny_Silver
김태현
이전 포스트

[자료구조] 3. Linked List

다음 포스트

[자료구조] 5. Priority Queue, Heap

0개의 댓글