210818 FUNDAMENTAL 24. Likelihood

• 머신러닝의 목표 : 모델이 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적의 파라미터 값을 찾는 것

1. 확률 변수로서의 모델 파라미터

ex) $y = f(x) = ax + b \qquad a, b \in \mathbb{R}$

• 파라미터 공간(parameter space) : (a,b)가 위치하는 $\mathbb{R}^2$ 공간
  
• 파라미터 공간에 주어진 확률분포
  • 파라미터 공간에 주어진 확률 분포는 평균이 (1,0)인 정규분포
  • a와 b의 값이 각각 1과 0에 가까울 확률
    ∴ 모델이 $y=x$에 가까울 확률이 크다고 보는 것
    

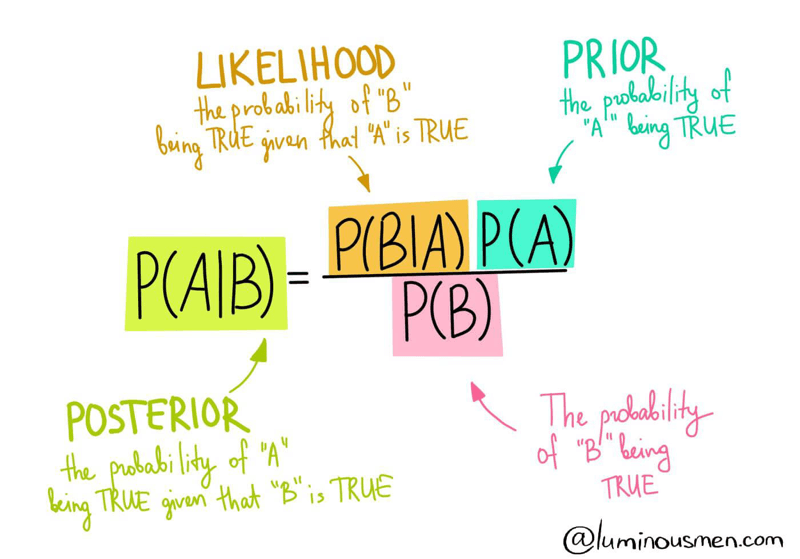
2. posterior, prior, likelihood

• 베이지안 머신러닝 모델 : 데이터를 통해 parameter들의 공간의 확률 분포를 찾아가는 과정(학습)
  

• prior(사전확률; prior probability) : 데이터를 관찰하기 전 파라미터 공간에 주어진 확률 분포 $p(θ)$

• likelihood(가능도, 우도)

  • 파라미터의 분포 $p(θ)$가 정해졌을 때 $x$라는 데이터가 관찰될 확률
  • $p(X=x|\theta)$ = $L(\theta|x)$
  • 우리가 구하고 싶은 것은 모델의 파라미터 $θ$의 값이고, 데이터는 이미 알고 있는 고정된 값
  • likelihood가 높다 : 우리가 지정한 파라미터 조건에서 데이터가 관찰될 확률이 높다 ⇨ 데이터의 분포를 모델이 잘 표현하는 것

• 최대 가능도 추정(maximum likelihood estimation, MLE) : 데이터들의 likelihood 값을 최대화하는 방향으로 모델을 학습시키는 방법

• posterior(사후 확률; posterior probability) : 데이터를 관찰한 후 계산되는 확률

• MAP(최대 사후 확률 추정; maximum a posteriori estimation) : posterior를 최대화하는 방향으로 모델을 학습시키는 방법

• 확률변수 X와 $θ$의 조건부 확률(joint probability)$p(X, θ)$
  $p(X,θ)=p(θ∣X)p(X)=p(X∣θ)p(θ)$
  양변을 $p(X)$로 나누면
  $p(θ∣X)= {p(X∣θ)p(θ)}/{p(X)}$
  즉, (posterior= {likelihood×prior}/{evidence}, posterior∝likelihood×prior)

3. likelihood와 머신러닝

• 입력 데이터의 집합을 $X$, 라벨들의 집합을 $Y$라고 할때, likelihood는 파라미터와 입력 데이터가 주어졌을 때 출력값(라벨)의 확률 분포 , 즉 $p(Y|\mathbf{\theta}, X)$
• 잔차(노이즈)의 분포가 $\mu = 0, \sigma = \sigma$로 가정하면
  
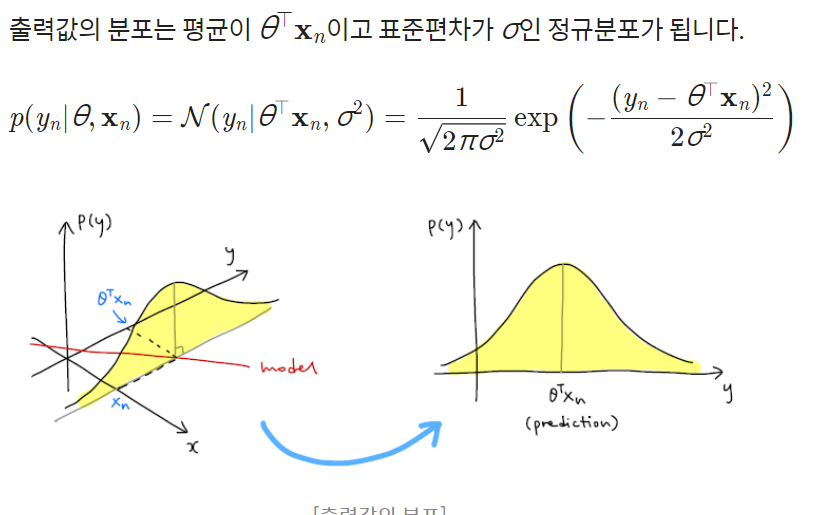
• 예측값과 라벨의 차이가 조금만 벌어져도 likelihood 값은 민감하게 반응
• 머신러닝의 목표가 데이터 포인트들을 최대한 잘 표현하는 모델을 찾는 것이었다 ⇨ 결국 데이터 포인트들의 likelihood 값을 크게 하는 모델을 찾는 것
• MLE(최대 가능도 추론; maximum likelihood estimation): likelihood 값을 최대화하는 모델 파라미터를 찾는 방법

4. MLE: 최대 가능도 추론

• 어떻게 정리하냐......

5. MAP: 최대 사후 확률 추정

• 머신러닝 모델의 최적 파라미터를 찾는 방법
  ||MLE|MAP|
  |---|---|---|
  |

---

참고자료
1. 베이지안 통계와 머신 러닝
2. 베이즈 정리의 의미