Batch
- GPU가 한번에 처리하는 데이터의 묶음
- Iteration 1회당 사용되는 training data set의 묶음
- Iteration은 정해진 batch size를 사용하여 학습을 반복함
- 장점 : GPU의 병렬연산 기능을 최대한 활용하여 학습속도를 줄일 수 있음
- ex)
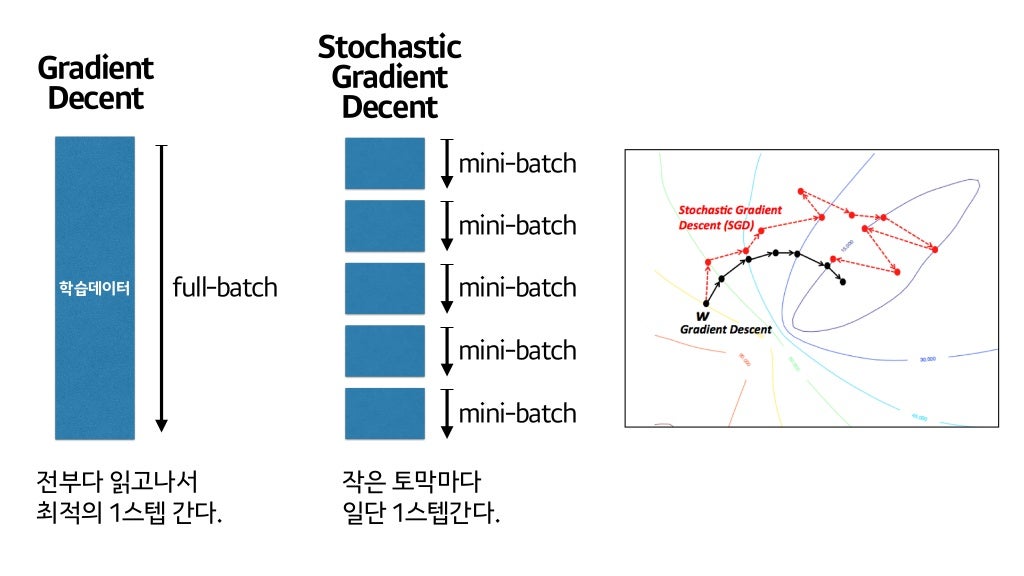
BGD vs SGD(full vs mini 와 합칠 것)
| BGD(Batch Gradient Descent) 배치 경사 하강법 | SGD(Stochastic Gradient Descent) 확률적 경사 하강법 | Mini-batch SDG(MSDG) 미니 배치 확률적 경사 하강법 | |
|---|---|---|---|
| 특징 | 1. 학습데이터 전체가 하나의 배치 (배치 크기 n) 2. 가장 업데이트 횟수가 적음 | 1. 전체 데이터 중 단 하나의 데이터를 이용 (배치 크기 1) 2. 기울기의 방향이 매번 크게 바뀜 | 데이터를 작게 나눠 그 중 일부를 학습에 사용 (Mini batch 개수 = batch size) |
| 장점 | 수렴이 안정적 | 적은 데이터로 학습하기 때문에 속도가 빠름 | 계산량이 적어 훈련 속도가 빠름 |
| 단점 | 전체 데이터를 모두 한 번에 처리하여 메모리가 가장 많이 필요 | 1. Global Minimum에 수렴하기 어려움 2. 노이즈가 심함 | 매번 정확한 gradient를 얻을 수 있는 것은 아님 |
| 시각화 |  |  |  |
| 예시 |  | 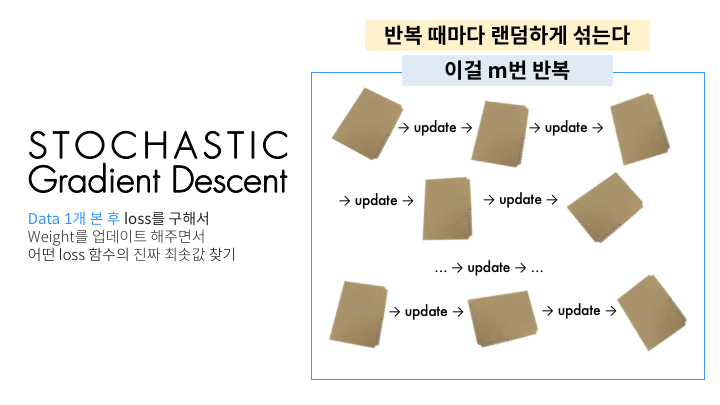 |  |
SGD 문제점
- 손실함수의 모양에 따라 영향을 많이 받는다.
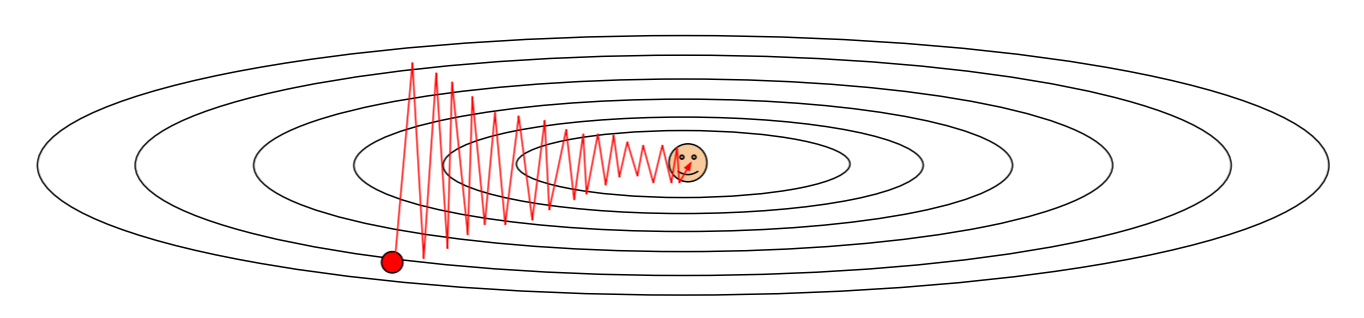
- local minima & saddle point 모두 valley에서 SGD가 멈춤
(∵opposite gradient = 0 : locally falt)

Gradient Descent Optimization Algorithms(Optimizer 종류)
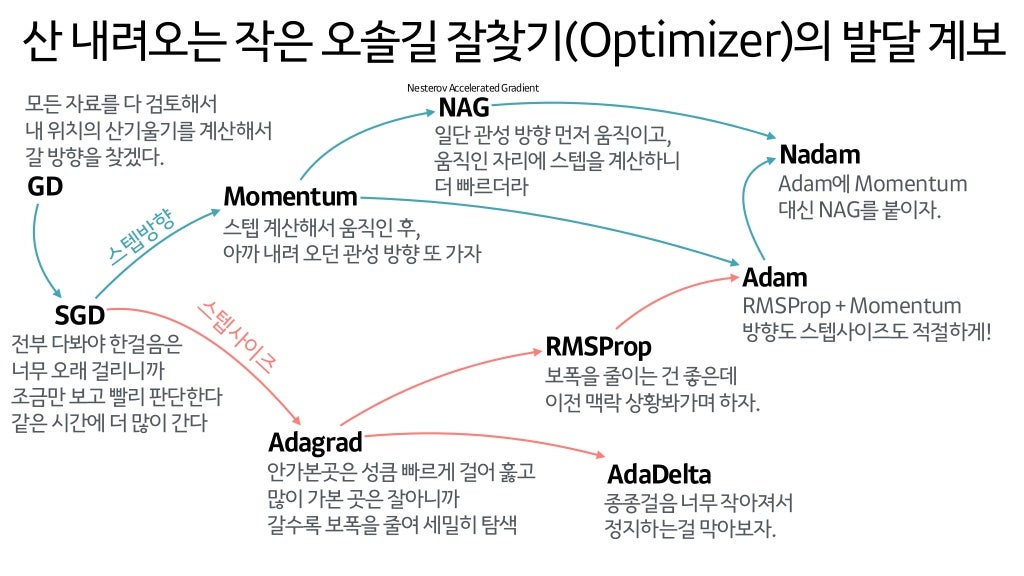
1) momentum term (rho)추가
- velocity(속도)의 영향력을 rho(0.9 또는 0.99)로 맞춤
- loca minima에 도달하여도 velocity(속도)를 가지고 있어 gradient = 0 이어도 움직임
- poor conditioning일 때, 수직 변동을 줄이고 수평 방향의 움직임을 가속시킴
(∵ momentum을 추가하면 high condition number problem 해결에 도움이 되므로)

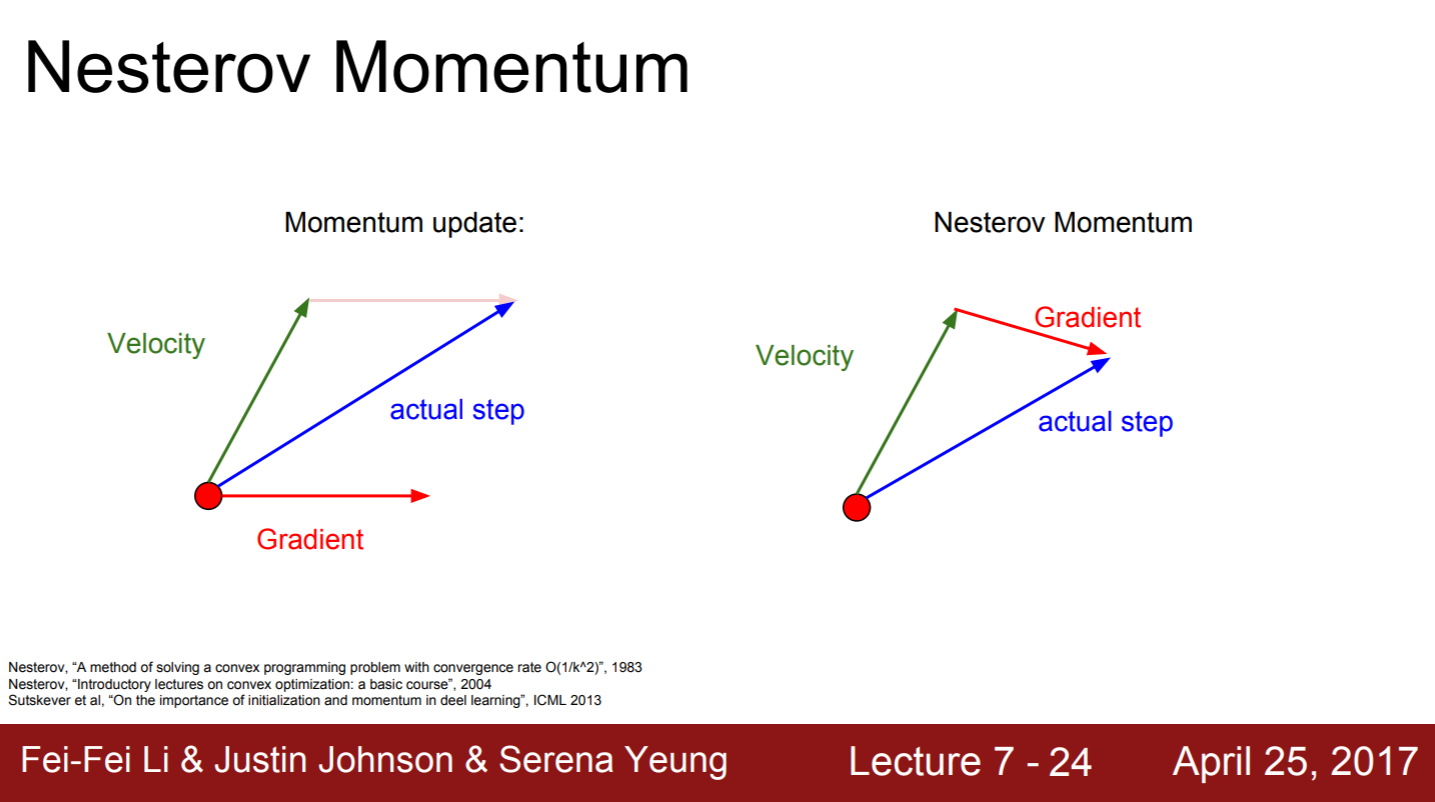
2) Nesterov Moment
- 특징 : Convex Optimization 문제에서 뛰어난 성능을 보임.
- Convex Optimization(블록 함수 최적화) : Logistic Regression에 대응하는 최적화 문제
- 장점 : velocity의 방향이 잘 못되면 gradient 방향을 더 활용하여 사용이 가능함
- 단점 : NN, non-Convex problem에서 까지 보장하지 못함
momentum이 좁고 깊은 minima를 무시하는 것이 버그가 아니고 momentum의 특징임
3) AdaGrad
-
훈련 중의 gradient를 활용하는 방법
-
grad squared term을 이용
-
-
단점 : 학습 횟수(t)가 계속 증가 ⇨ step은 점점 값이 작아짐
-
실제로는 잘 안씀
non-convex case에서 saddle point를 만나면 AdaGrad는 멈춰버림
non convex case vs convex case가 무엇인지 정리
4) RMSProp
- AdaGrad의 단점을 보안한 알고리즘
- 기존 누적값에 decay-rate(0.9 또는 0.99)를 곱함
- 특징 : velocity(속도)가 줄어들던 문제를 해결함. 각 차원마다 적절한 궤적(trajectory)를 수정
- AdaGrad의 Learning rate를 늘리면 RMSProp 와 비슷해짐
convex case에서 AdaGrad를 visualization 하고 싶다면 알고리즘별 Learning rate를 조정해야 함
5) Adam = RMSProp + momentum = second wauared gradient + mometum
- 가장 많이 사용
- 단점 : NN과 poor conditioning에서는 오래걸림
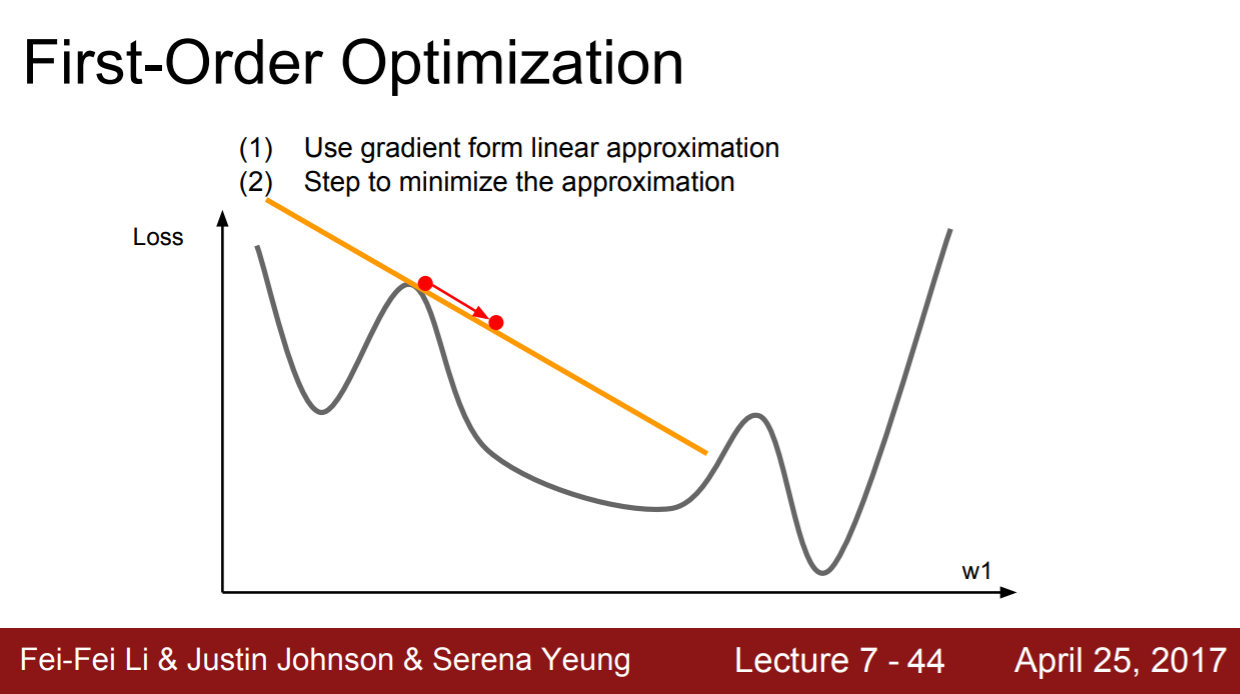
First-order vs Second-order(블로그 보고 내용 추가)
| First-order | Second-order |
|---|---|
| 1차 테일러 근사 (Linear approximation) | 2차 테일러 근사 (Quadratic approximation) |
| 일반적으로 많이 사용되는 방법 직선의 기울기 구하는 방식 | 2번의 미분을 진행함 이차곡선의 최솟값을 찾아 다이렉트로 이동함 |
| 단점 : 메모리를 많이 잡아먹음 | |
 |  |
- Newton stem
- 특징 : Learning rate가 불필요
- 단점 : 메모리 이용이 많음. 딥러닝에서는 사용 안 함
- L-BFGS(Limited-memory BFGS)
- full batch update, fewer parameter와 less stochastic일때 선택하는 방법
- 단점
- stochastic case에서 잘 동작하지 않기 때문에 딥러닝에서 사용하지 않음
- non-convex problem에도 적합하지 않음
정규화
- L1
- L2
- Dropout
<참고자료>
1. MGD, SGD의 차이
2. SGD에서 배치 사이즈가 학습과 성능에 미치는 영향
3. Linear Regression(4) : GD, BGD, SGD, MB-SGD, SGD issues
4. 배치와 미니 배치, 확률적 경사하강법 (Batch, Mini-Batch and SGD)
5. Training Neural Networks II
6. Deep Learning - Optimizer 종류와 개념
<읽어볼 자료>
