✨ 선행 : Chain Rule(미분의 연쇄 법칙)
-
chain rule(연쇄법칙) : ‘합성 함수’를 미분할 때의 계산 공식
1. Backpropagation 역전파 알고리즘
- Artificial Neural Network를 학습시키기 위한 일반적인 알고리즘 중 하나
- Perceptron 퍼셉트론 : 초기 인공신경망 모델
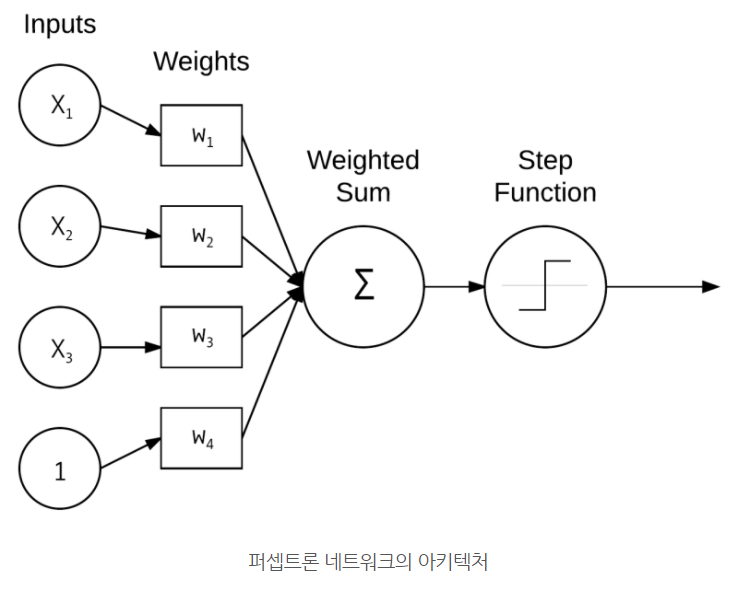
- 어려워 보이지만 AND, OR 연산도 단층 퍼셉트론

- XOR 연산은 다층 퍼셉트론(퍼셉트론/게이트 여러개 연결)
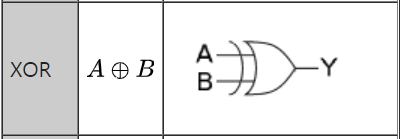
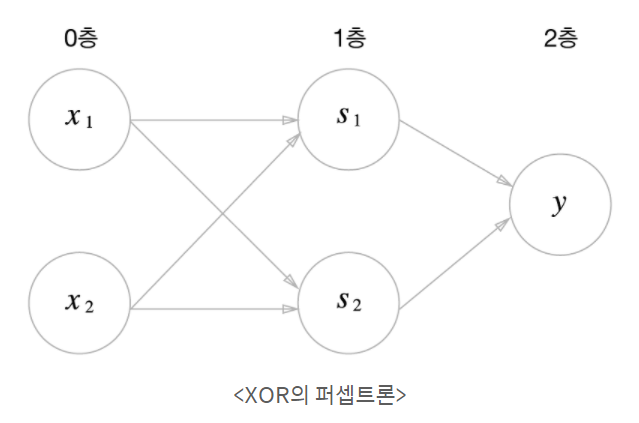
- Perceptron 퍼셉트론 : 초기 인공신경망 모델
- input에서 output까지 가중치를 업데이트하면서 활성화함수(sigmoid, rule등)를 통해 결과값을 냈다면,
- 역전파 알고리즘은 그렇게 도출된 결과값을 통해 다시 output에서 input까지 역방향으로 가면서 가중치를 재업데이트를 해주는 방법

- 왜 역전파를 하는 것일까?
- 수치미분을 통하여 신경망을 갱신하려면, 미분 과정에서 delta값을 더한 순전파를 몇번이고 다시 행해야 합니다.
- 즉, 연산량이 多.
- 그러면 더 복잡하고 더 큰 규모의 딥러닝을 순전파로 몇번이고 학습을 수행하면서 적절한 가중치 값을 찾고자 한다면 매우매우매우 비효율적!
-
그래서 고안된 방법이 경사하강법(gredient descent)
-
단계적으로 함수의 기울기를 이용해서 값이 가장 낮아지는 곳을 찾는 것
-
why? 머신러닝에서는 가중치의 그래디언트(미분값)가 최소가 되는 지점이 손실함수를 최소로 하는 지점일 것라고 가정함
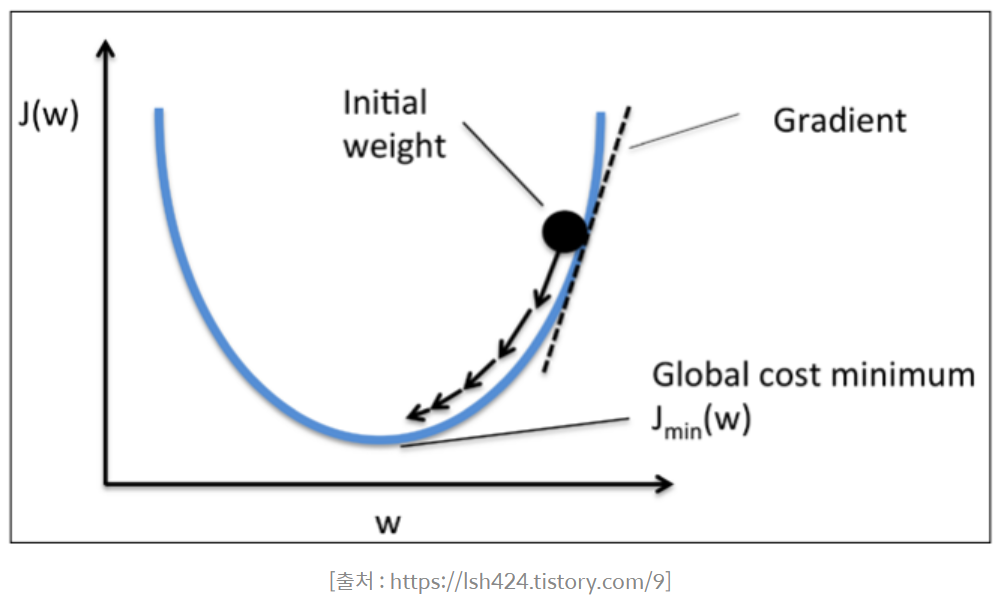
-
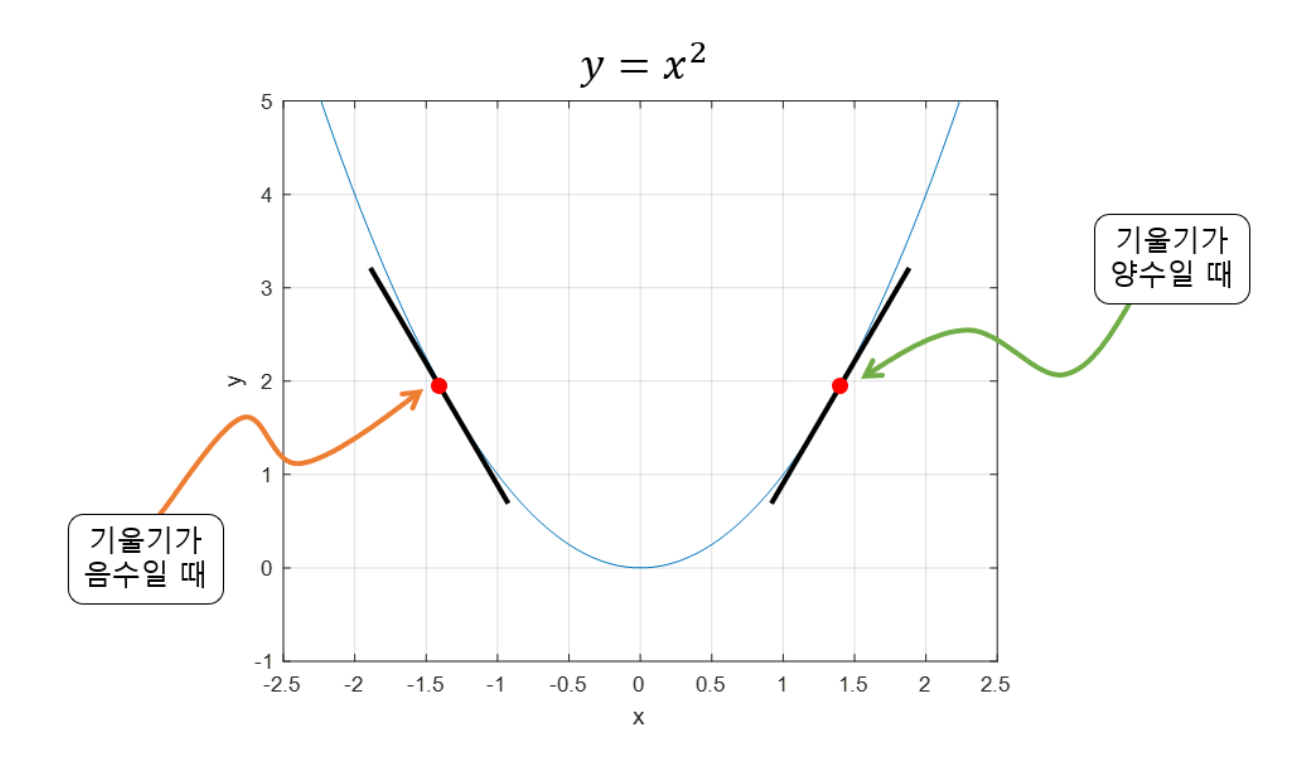
"기울기의 값이 크다"
= 가파르다
= x의 위치가 최소값/최댓값에 해당되는 x 좌표로부터 멀리 떨어져있다
-
그래디언트 값을 다음과 같은 식으로 업데이트를 합니다.
-
<예제 1>
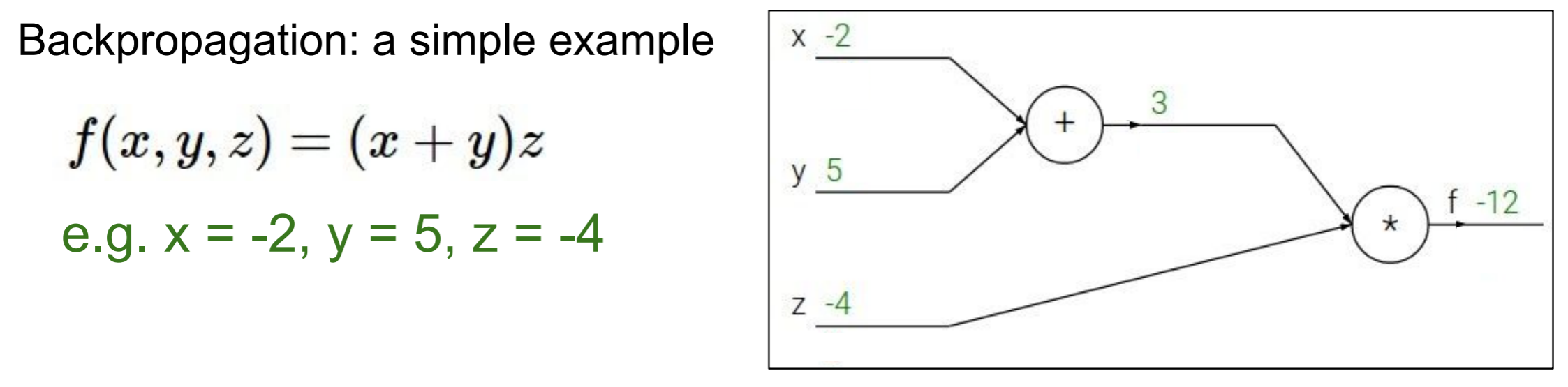
-
미분을 한다는 것은 변화량을 보고자 하는 것!
-
여기서, 궁극적으로 구하고자 하는 것은 (df over dx라고 읽음).
-
의미는 가 1만큼 변했을 때 가 얼마만큼 변하는 가 ⇨ 즉, 변화량을 보려고 하는 것
- (dq over dx라고 읽음)의 의미는 가 얼마만큼의 변화를 가졌을 때 는 얼마만큼의 변화를 가졌는 가?를 나타냄.
- 만약 라면 가 1일때 는 2만큼의 변화량을 같는다 라고 해석할 수 있음.
-
local gradient
-
global gradient
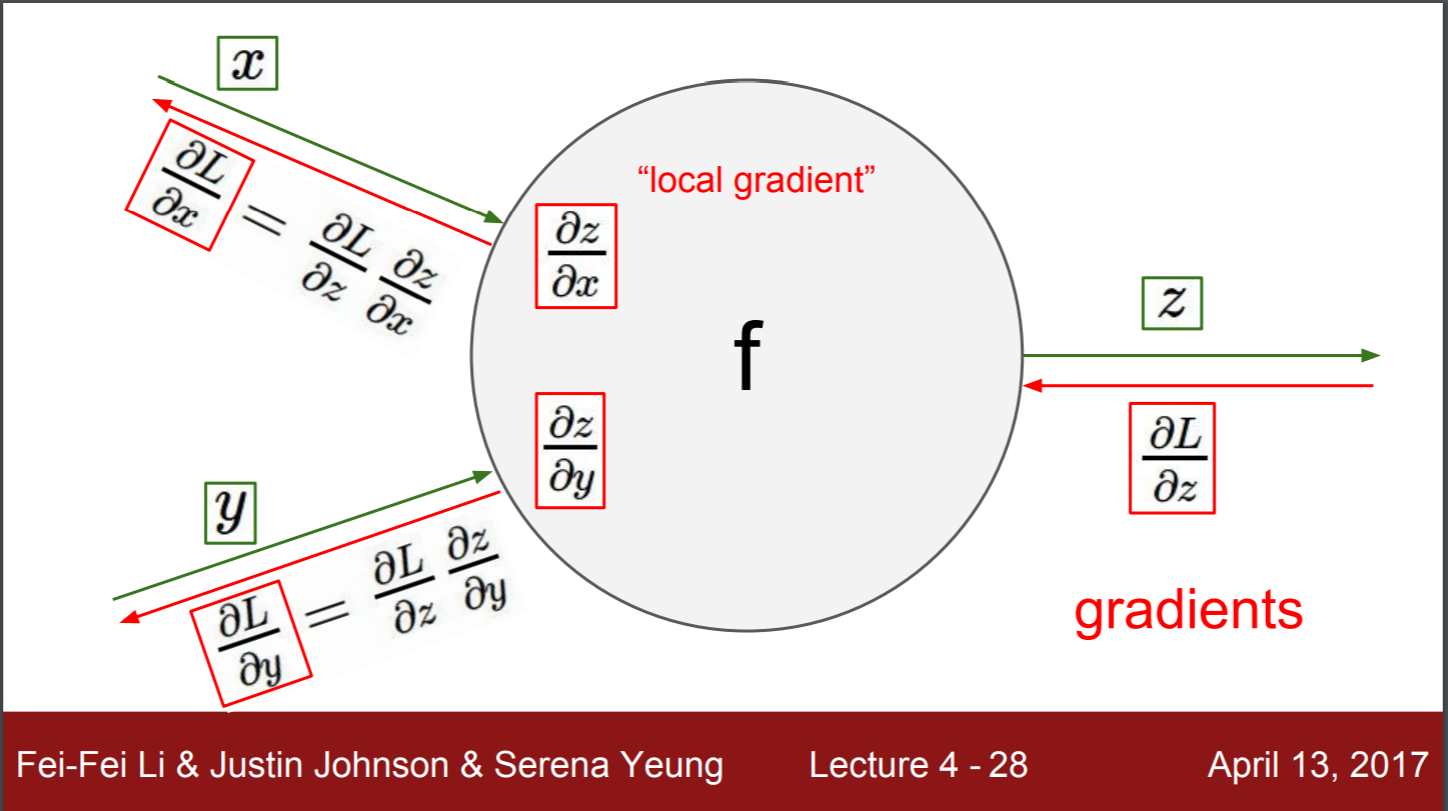
-
노드가 분기될 때 어떻게 해야 할까? 더해주면 된다.
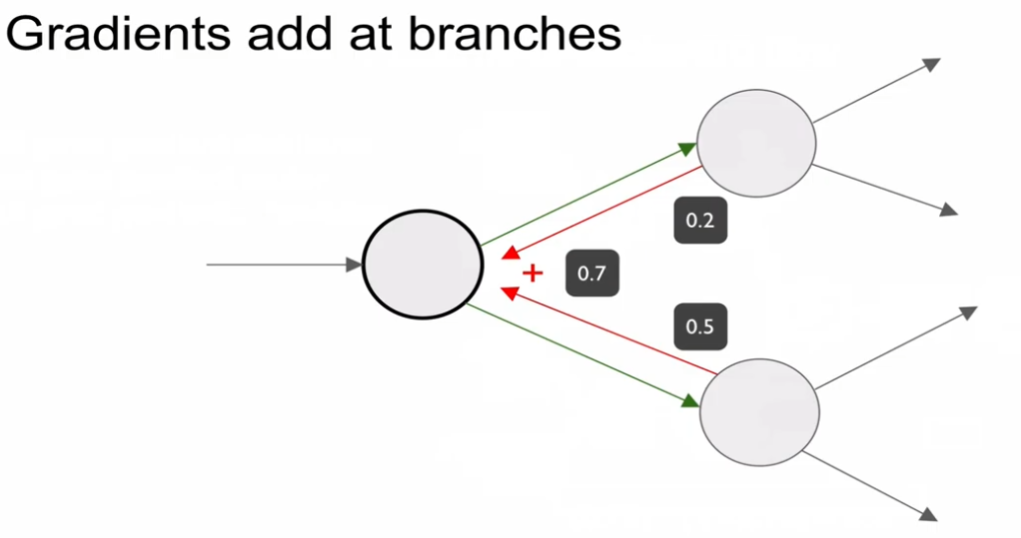
<예제 2>

<예제 3> 야코비안 행렬(Jacobian matrix) : Vector 값이 주어졌을 때 gradien

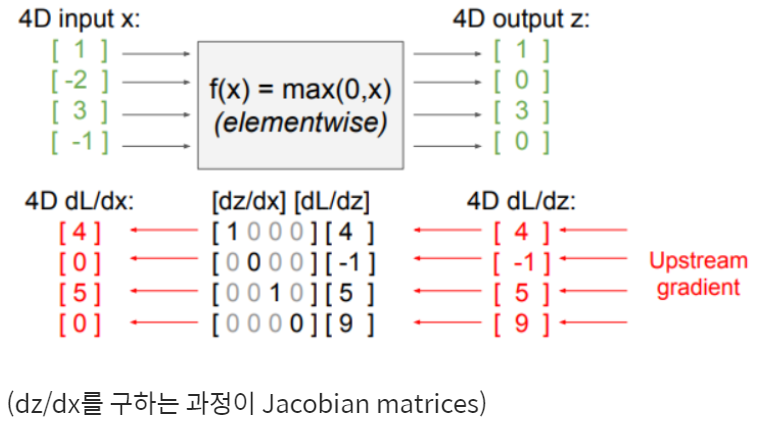
- 야코비안 행렬 (jacobian matrix)을 계산하는데에도 역전파 전개 방식을 도입
- 야코비안 행렬은 백터를 출력하는 1차 미분 행렬
- 즉, 출력 값이 하나의 실수 값(스칼라)이 아니라 벡터(행렬)
- sparse structure 구조를 갖는다
- 행렬 곱 특징을 통해 Jacobian matrix의 크기는 4096 x 4096 크기를 갖는다.
- 행렬 곱
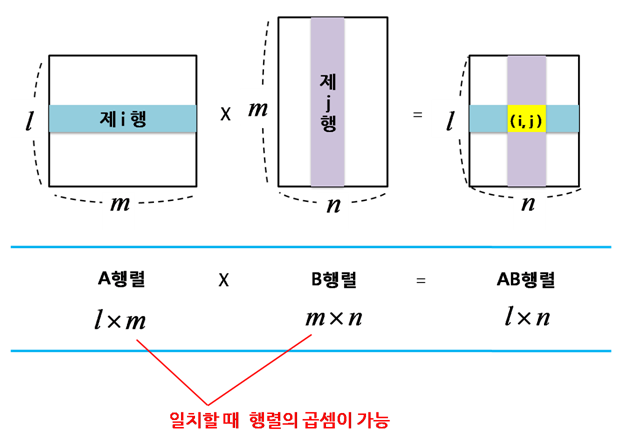
- 행렬 곱
<예제 4> 선형 함수 결과값에 L2 정규화를 적용하는 예
2. Neural Network 신경망
- hidden 노드 각각은 class를 의미한다.
- parameter approach(1:N class fyer) 중 하나

- 생명체의 뉴런이 작동하는 방식에서 착안
- 그렇다고 실제 신경망이라고 할 수 없다.
| 신경계 | 컴퓨터 |
|---|---|
 | 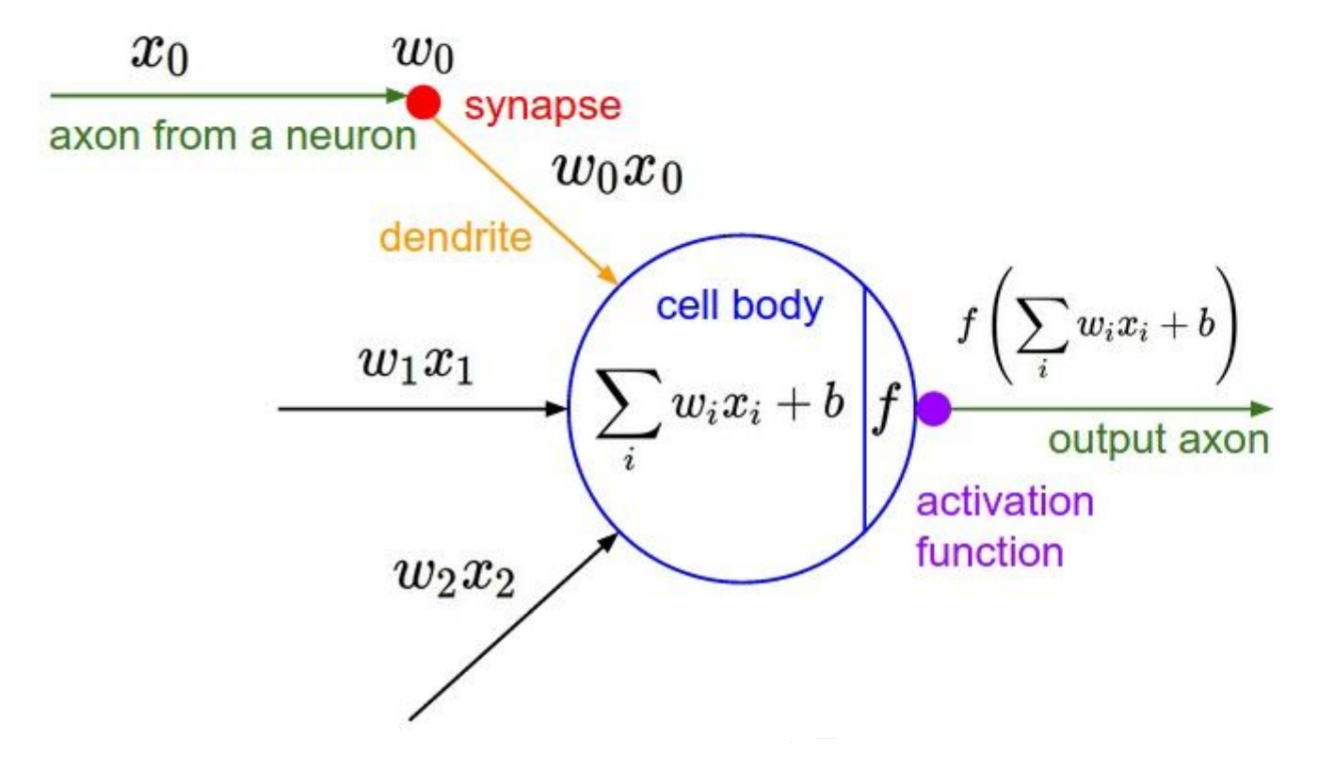 |
- 활성함수(activation function)의 종류

- "Fully-connected" layers : 완전연결 계층
- 한 layer의 모든 뉴런이 그 다음 layer의 모든 뉴런과 연결된 상태
- Fully connected layer = FC layer = Dense layer
- 모두 연결되었다는 것은 행렬곱을 수행한다는 것을 의미
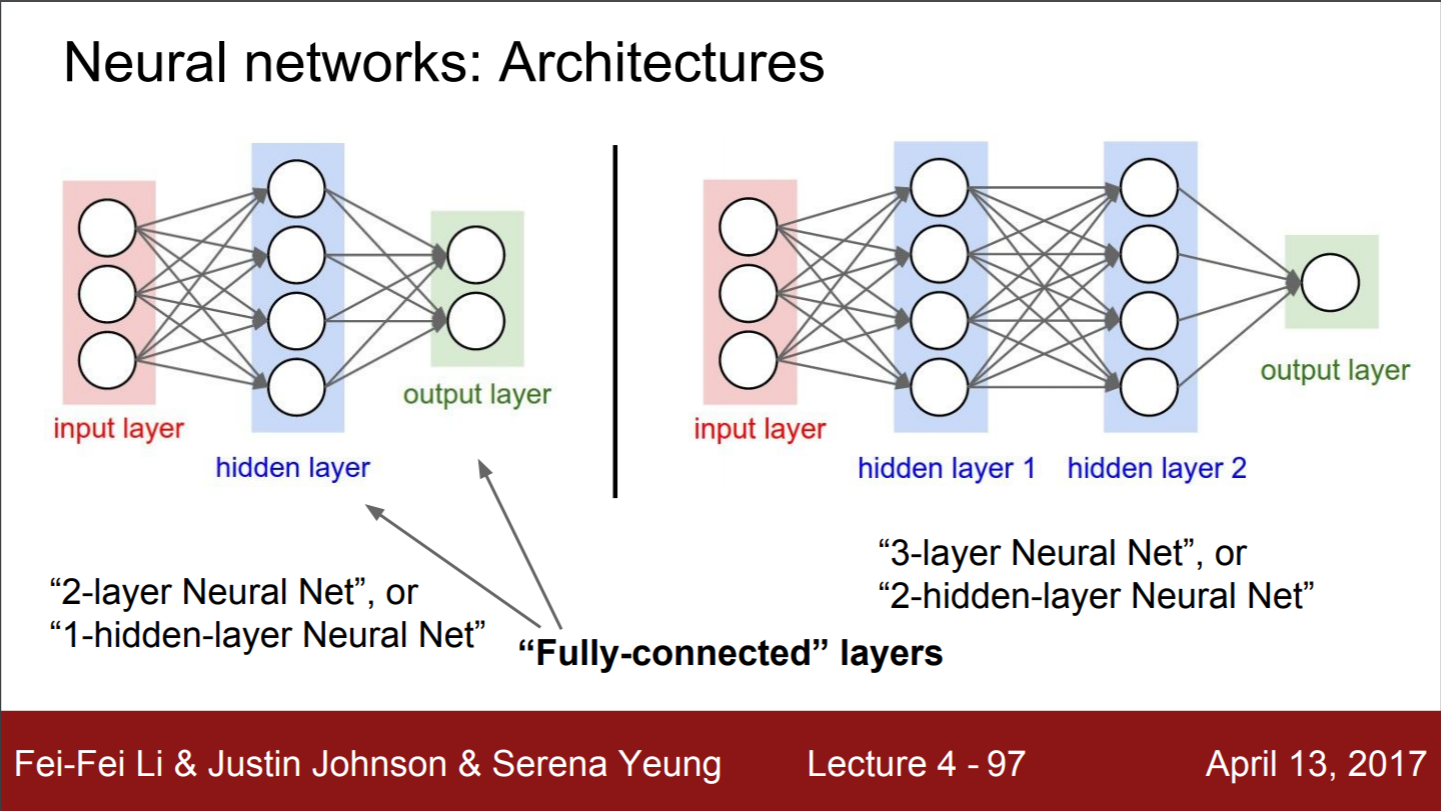
- 레이어로 구성되어 편의성이 있음
- 하나의 단일 레이어는 단일 연산으로 끝을 낼 수 있음
- layer의 사이즈 크기 조절은 어떻게 할까?
- 많아 질수록 capacity가 높아진다.(분류 능력이 좋아진다.)
- bigger = better(but might have to regularize more strongly)
- NN 사이즈가 정규화(regularization)로서 역할은 아니다.
- 데이터의 오버피팅이 일어나지 않고도 NN을 구성하는 옳은ㅇ 방법은 네트웍을 작게 만드는게 아니고 regularization sequence()를 높여줘야 한다.
--
용어 정리
- identity function
- sparse matrix : 대부분 0으로 채워진 행렬 ↔ dense matrix
참고자료
1. 문과생도 이해하는 딥러닝 (3) - 오차 역전파, 경사하강법
2. #1-(3) 퍼셉트론 : XOR 게이트
3. 밑바닥부터 시작하는 딥러닝 ch2. 퍼셉트론
4. 딥러닝 학습시 오차 역전파를 사용하는 이유
5. 경사하강법(gradient descent)
6. Error Backpropagation
7. 머신러닝: 역전파
8. 모두를 위한 cs231n-Lecture4
9. 편미분을 간단하게 Jacobian Matrix
10. 완전연결계층
다른 cs231n 강의노트 정리
1. https://lsjsj92.tistory.com/393
2. https://m.blog.naver.com/wpxkxmfpdls/221846678837
3. https://dsbook.tistory.com/59
4. https://m.blog.naver.com/vi_football/221878546500