👨‍🏫학습목표

오늘은 Monte Carlo method와 MC Prediction 그리고 Incremental Mean에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=eibrMjPEAMg&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=11

1️⃣ Monte Carlo method

🔷 Monte Carlo

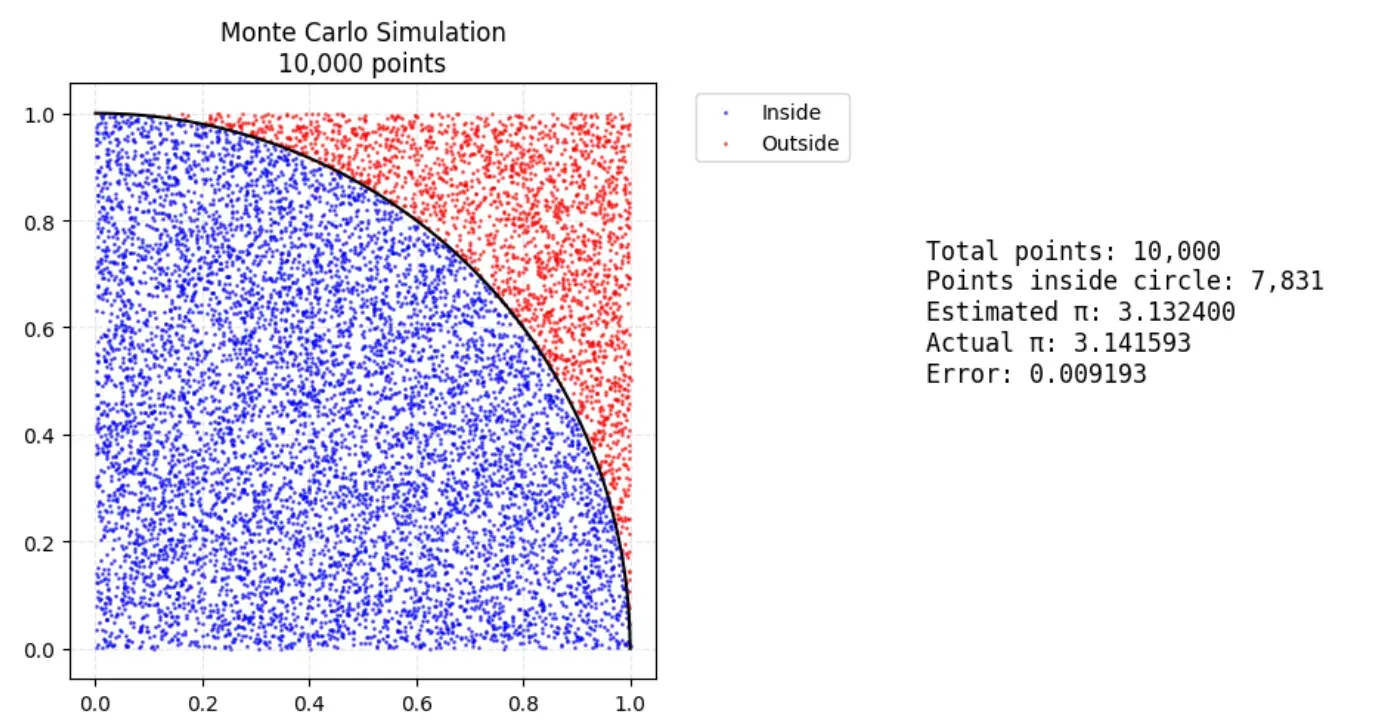
출처: https://medium.com/@miyoko_shimura/monte-carlo-simulation-using-python-random-sampling-by-calculating-π-be3cdd326361

• Random sampling을 통해서 특정 수치적 결과를 얻는 방법이다.

• Q-table (Action-value function table)을 사용한다.

• MC Policy Iteration은 Episode를 하나의 단위로 하여 GPI를 수행한다.

• 하나의 sample은 하나의 episode의 끝 terminal state까지의 단계를 포함한다.

• Sample data의 state만 고려하여 계산하기 때문에 연산량이 적다.

• Monte Carlo는 Markov property를 일부 따르지 않더라도 큰 문제가 없다.

• $Q(s,a)$를 업데이트하기 위해서는 $G_t$ 혹은 $R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})$를 사용할 수 있는데, Monte Carlo는 $G_t$를 사용하여 업데이트하기 때문이다.

• 반면, 이후에 살펴볼 Temporal Difference (TD)는 $R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})$를 사용하여 $Q(s,a)$를 업데이트 하기 때문에 Markov property를 따르지 않을 경우 문제가 발생한다.

---

2️⃣ MC Prediction

🔷 MC Prediction

• Dynamic Programmin에서는 모든 state를 계산하기 때문에 evaluation이라는 표현이 적합하지만, Monte Carlo에서는 sample data만으로 추정을 하기 때문에 prediction이라는 표현이 더 적합하다.

• 목표: 현재 policy에서 model이 경험을 통해 하나의 episode sample을 수집한 후, 해당 정보를 이용하여 $q_\pi$를 구하는 것이다.

• Episode 정보: $S_0, A_0, R_1, S_1, \dots, R_T, S_T$

• Return: $G_t = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{T-t-1} R_T$

• Action-value function: $q_\pi(s, a) = \mathbb{E}_\pi[G_t | S_t = s, A_t = a]$

❗ 여기서 잠깐

Monte Carlo는 sample을 이용하여 계산하기 때문에 $E$ 기대값을 구할 수 없다. 따라서 하나의 시나리오에 대한 sample들의 $G_t$의 평균을 대신 사용한다.

또한 하나의 시나리오 안에서도 동일한 $(s, a)$ 쌍이 나타날 수 있다. 첫 번째 쌍만 사용할지, 모든 쌍을 사용할지에 따라 First-Visit MC와 Every-Visit MC로 나뉜다.

• 각 state-action 쌍에 대한 return의 평균을 구할 때, 각 return이 서로 독립이고, sample의 수가 충분히 크다면 큰 수의 법칙에 따라 $Q(s,a) \rightarrow q_\pi(s,a)$를 만족한다.

• 이러한 각 $Q(s,a)$를 계산하는 과정을 조금 더 간단하게 만든 것이 Incremental mean이다.

---

3️⃣ Incremental Mean

🔷 Incremental mean

• 정리하면 아래와 같다.

🔷 Incremental Monte Carlo updates

• Episode 정보: $S_0, A_0, R_1, S_1, \dots, R_T, S_T$

$n(S_t, A_t) \leftarrow n(S_t, A_t) + 1$

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \frac{1}{n(S_t, A_t)} [G_t - Q(S_t, A_t)]$

• 모든 $G_t$를 기억할 필요 없이 이전 $Q(S_t, A_t)$와 새로운 $G_t$에 대한 정보만 알고 있으면 된다.

• 그런데 Reinforcement Learning에서 model은 시간이 지날수록 성능이 개선된다.

• 따라서 미래에 얻게 되는 Return $G_t$가 더 중요하다는 의미이기도 한다.

• 하지만 현재 방식은 모든 시간의 $G_t$를 동등한 중요도로 보고 평균을 구하는 방식이다.

• 이러한 한계를 극복하기 위해 새로운 방식이 등장한다.

🔷 Constanst - $\alpha$ MC Policy Evaluation

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [G_t - Q(S_t, A_t)]$

• $\frac{1}{n(S_t, A_t)}$대신 상수 $\alpha$를 사용한다.

• $\alpha$를 사용하게 되면 최근의 Return $G_t$를 더 많이 반영하는 효과가 나타한다.

• 또한 $\frac{1}{n(S_t, A_t)}$를 계속 연산하지 않기 때문에 연산량이 감소한다.

• 또한 model의 성능은 계속해서 좋아지기 때문에 $G_t$는 엄밀하게 보면 $iid$를 만족하지 않는다.

• 식을 정리하면 아래와 같다.

$Q(S_t, A_t) \leftarrow(1 - \alpha) Q(S_t, A_t) + \alpha G_t$

• Old episode를 $(1-\alpha)$만큼 감소시키는 효과가 있다.

---

4️⃣ 정리

🔷 11강에서 배운 내용은 아래와 같다.

1. Monte Carlo method에 대해 배웠다.
2. MC Prediction 단계에서 $q_\pi(s, a)$를 추정하는 방법을 살펴보았다.
3. Incremental Monte Carlo를 배웠다.
4. 최근의 Return $G_t$를 더 많이 반영하는 Constanst - $\alpha$ MC Policy Evaluation를 살펴보았다.