👨‍🏫학습목표

오늘은 Deep Q-Network과 Naïve DQN의 개념, Naïve DQN의 한계, 이를 극복하기 위한 Experience Replay에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=eBIdI1hntf8&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=17

1️⃣ Deep Q-Network

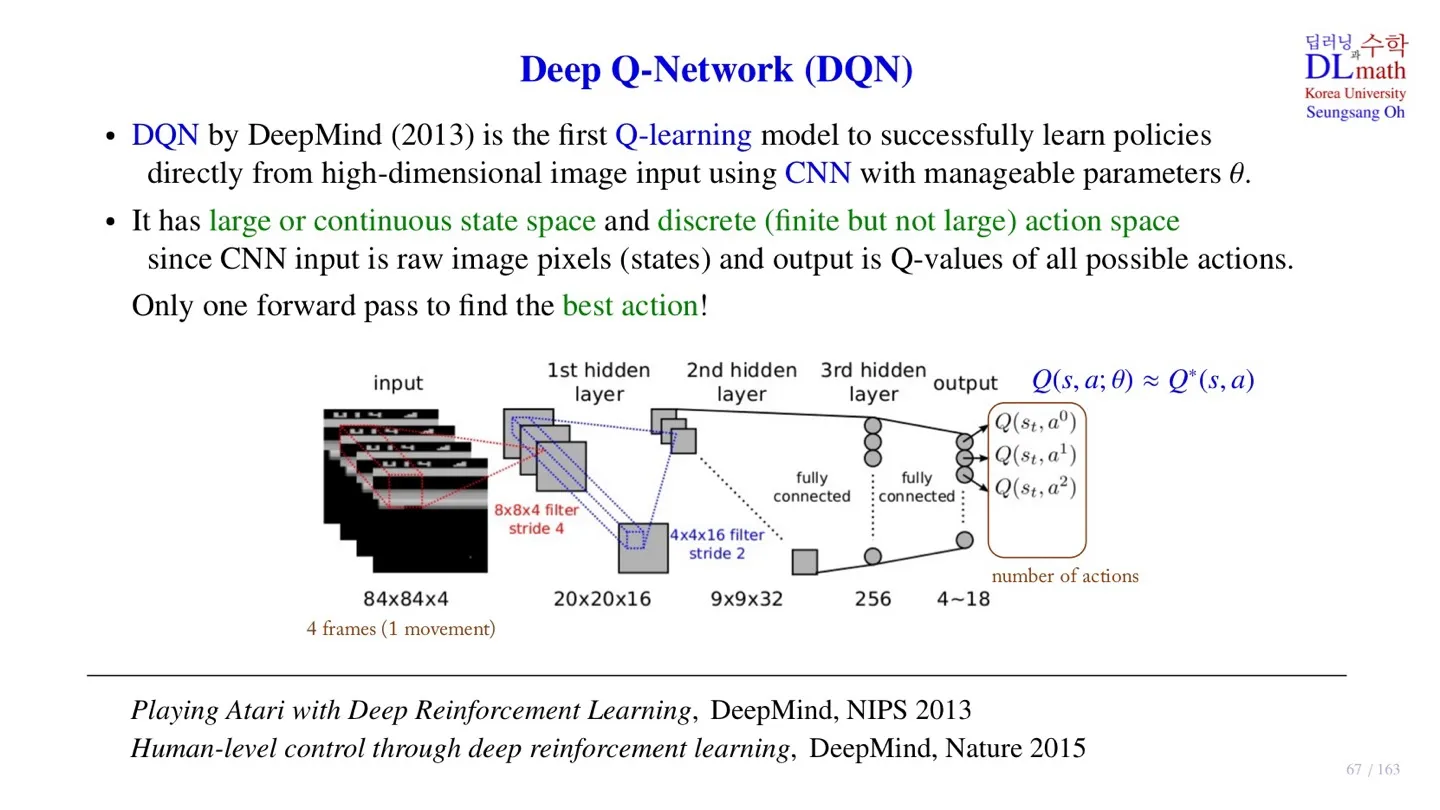
🔷 Deep Q-Network

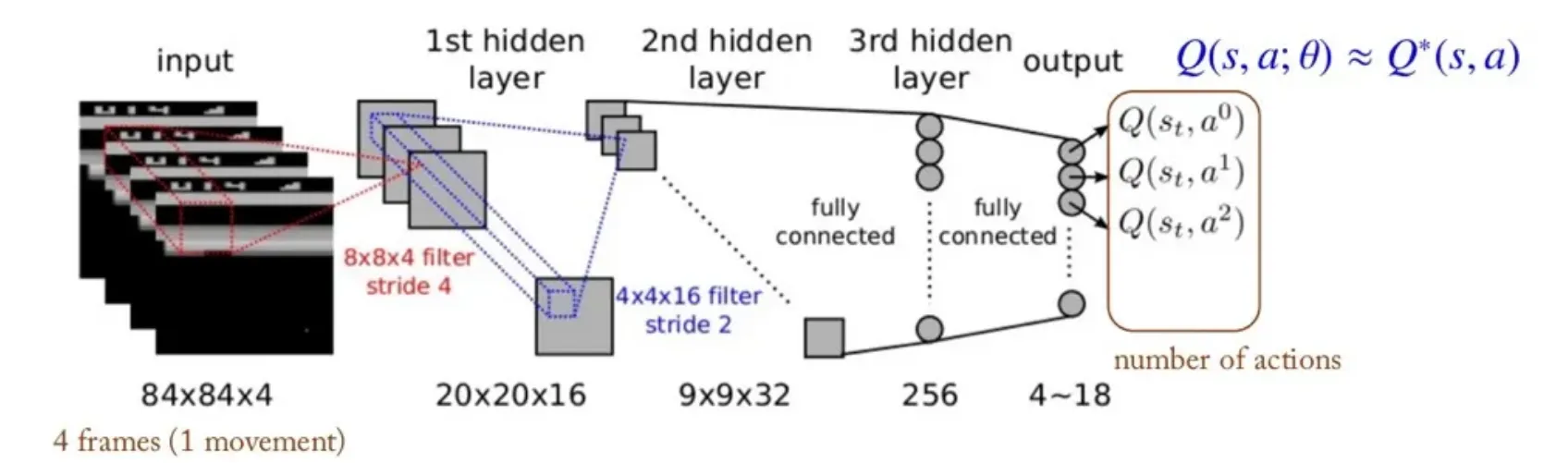
• 2013년 DeepMind에서 발표하였다.
• RL의 Q-learning과 CNN을 결합하여 개발하였다.
• Q-Network를 통해 $Q(S_t ,\ a;\, \theta)$를 근사한다.
• 입력 데이터: $S_t$, Atari game의 화면
• 출력 데이터: $Q(s,a)$, Atari game의 action 수
• 출력 데이터에서 가장 큰 $Q(s,a)$를 선택하여 Q-learning을 진행한다.
• State space의 크기가 크거나 Continuous한 데이터도 처리 가능하다.
• 하지만 출력 데이터의 dimension은 아직 finite하다.

📃 논문

• Playing Atari with Deep Reinforcement Learning

---

2️⃣ Naïve DQN

🔷 Q-learning

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]$

• Target policy $R_{t+1} + \gamma \max_a Q(S_{t+1}, a)$와 Behavior policy $Q(S_t, A_t)$의 간격을 좁히는 방향으로 학습한다.

🔷 Naïve DQN

• 가장 기본적인 DQN이다.
• Q-learning에서 Q-table 대신 Q-Network를 적용한 모델이다.

$L(\theta) = [r_{t+1} + \gamma \max_a Q(s_{t+1}, a; \theta) - Q(s_t, a_t; \theta)]^2$

• Q-Network에서 ****$\max_a Q(s_{t+1}, a; \theta)$를 얻는다.
• SGD 방식을 통해 MSE를 줄이는 방식으로 학습한다.
• 하지만 좋은 성능을 발휘하지는 않는다.

🔻 Naïve DQN의 한계

• Sample 사이에 temporal correlation이 존재한다.
• Target 값이 계속 바뀌는 non-stationary target 문제가 존재한다.

⚖️ 성능비교

	Breakout	R. Raid	Enduro	Sequest	S. Invaders
Naive DQN	3.2	1453.0	29.1	275.8	302.0
Linear	3.0	2346.9	62.0	656.9	301.3

• Naïve DQN: 3-Convolution layer, 2-FC layer
• Linear model: 1-FC layer
• 두 모델의 성능이 유사하고, 일부 영역에서는 Linear model이 더 좋은 성능을 발휘한다.

---

3️⃣ DQN

🔷 DQN

• DQN은 Naïve DQN의 한계를 극복하기 위해서 2가지 장치를 추가한다.

1. Experience replay: temporal correlation 문제를 해결하기 위해 추가하였다.
2. Target Network: non-stationary target 문제를 해결하기 위해 추가하였다.

• 그 외에도 Clipping reward를 사용한다.
  • 각 게임마다 점수 Scale이 달라 동일하게 적용할 Reward를 지정하였다.
  • Positive reward +1
  • Negative reward -1
• End-to-end RL : 입력 데이터로 game 이미지와 점수만 받는다.
• 동일한 모델 가중치로 다양한 game에서 좋은 성능을 발휘한다.

출처: https://www.youtube.com/watch?v=TmPfTpjtdgg

---

4️⃣ Experience Replay (Replay Buffer)

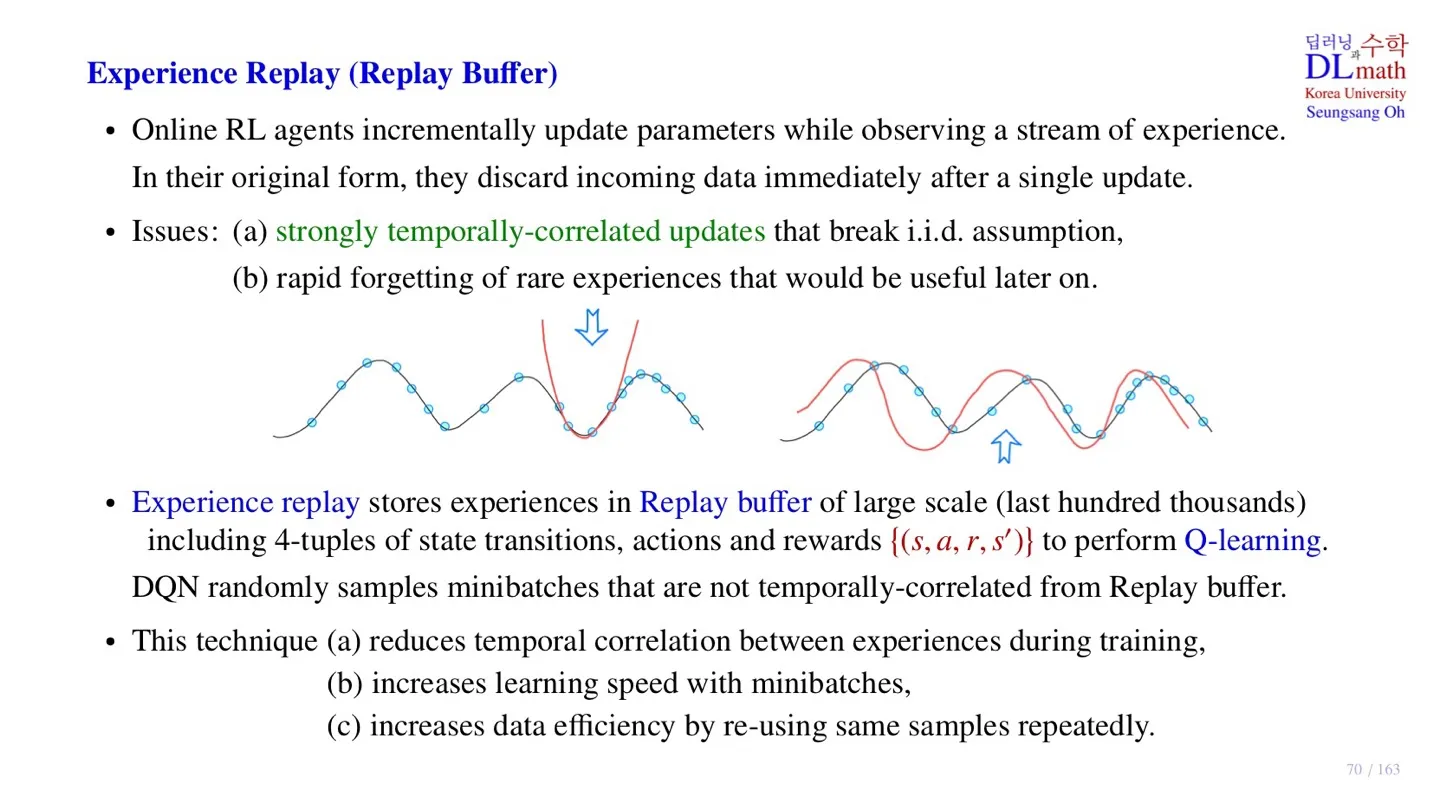
🔷 Experience Replay

• 지속적인 학습을 수행하는 Online RL agent는 sample data를 수집하여 업데이트 후 이를 버린다.

• 예를 들어 Robot이 넘어지는 상황을 가정하자. Robot은 조금씩 비틀거리면 넘어질 것이다. 하지만 Robot이 완전히 넘어지기 전까지는 Negative Reward를 받지 않는다. 완전히 넘어져야 Negative Reward를 받는 것은 좋은 상황이 아니다.

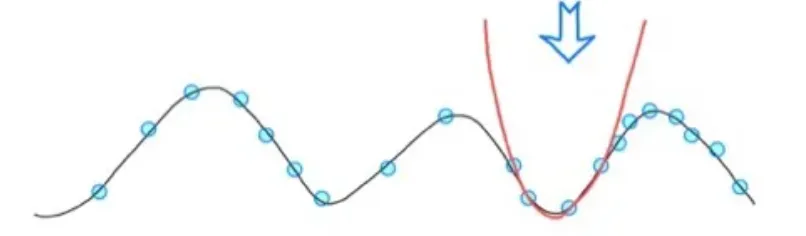
• 유사하게 우리가 sample data를 통해서 학습을 수행할 때 빨간선처럼 해당 sample data에서만 잘 적한된 학습을 원하는 것이 아니다. sample data 이전의 경우에서도 우리가 원하는 방향으로 학습할 수 있도록 설계해야 한다.

• DQN에서는 과거에 수집한 sample data를 가져와서 다시 학습을 진행한다.

🔻 Naïve DQN의 문제

• Online 학습에서는 시간 순으로 학습이 진행되기 때문에 이전 state에 크게 영향을 받는다.
• 이는 $i.i.d.$ assumption에 위배된다.
• 또한 학습 후 sample data를 버리기 때문에, 자주 등장하지 않는 data는 빠르게 망각한다.
• 하지만 자주 등장하지 않는 data가 중요한 경우 역시 존재한다.

🔻 Experience Replay 구현 방법

• sample data : $(s_t, a_t, r_{t+1}, s_{t+1})$
• 수집된 sample data를 Replay buffer에 저장한다.
• 학습을 진행할 때 Replay buffer에서 Random하게 sample을 추출하여 minibatch를 만든다.
• Random하게 추출되었기 때문에 temporally-correlated하지 않다.

🔻 Experience Replay의 장점

• 학습을 진행할 때, data에 존재하는 temporal correlation을 줄일 수 있다.
• 수집한 sample data와 저장된 data가 함께 학습되어 학습 속도가 빨라진다.
• 하나의 data를 반복적으로 사용하여 data efficiency를 높일 수 있다.

---

5️⃣ Diagram을 통한 Replay Buffer 이해

🔷 작동 순서

• Behavior Q-Network : CNN을 통해 Q-value를 출력하는 Network
• Replay Buffer의 크기는 100,000으로 제한한다.

🔻 Sample을 얻는 과정

1. state $s_t$가 주어졌을 때, 가장 큰 $Q(s,a;\theta)$를 출력하는 action $a_t$를 선택한다.
2. 해당 action과 나머지 action에 대하여 $\epsilon$-greedy를 적용하여 최종 action을 결정한다.
3. 해당 action을 Environment에 적용한다. (execute $a_t$ in emulator)
4. Reward $r_{t+1}$과 next state $s_{t+1}$을 얻는다.

🔻 Q-Network를 업데이트 하는 과정

5. 새로운 sample data $(s_t, a_t, r_{t+1}, s_{t+1})$를 Replay Buffer에 저장한다.
6. 저장된 data가 100,000개가 넘을 경우 가장 오래된 sample data를 제거한다.
7. Replay Buffer에서 minibatch 크기만큼 데이터를 sampling한다.
8. Sampling된 데이터를 통해 업데이트를 진행한다.

---

6️⃣ 정리

🔷 17강에서 배운 내용은 아래와 같다.

1. Deep Q-Network에 대해 배웠다.
2. Naïve DQN의 한계에 대해 살펴보았다.
3. Experience Replay에 대해 배웠다.
4. Diagram을 통해 Experience Replay의 작동방식을 배웠다.