👨‍🏫학습목표

오늘은 TRPO의 파라미터를 업데이트하기 위한 Natural Gradient Policy에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=Q3_mJFKiEwc&t=1060s

0️⃣ TRPO

📕 지난시간에 배운 내용

• TRPO는 모델의 성능을 monotonic하게 향상시키는 것에 초점을 맞춘 모델이다.
• 이를 위해서 Minorization-Maximization algorithm과 Trust region 개념을 사용한다.
• Trust region 안에서 MM-algorith을 사용하면 expected return의 monotonic improvement가 보장된다
• 그 결과 step size에 대해서는 크게 고려하지 않아도 된다.

---

1️⃣ TRPO의 object function

📕 지난시간에 배운 내용

• Expected return을 object function으로 사용한다.

---

2️⃣ Object function의 Lower bound

📕 지난시간에 배운 내용

• 여러 approximation을 통해 object function의 lower bound를 찾는다.

---

3️⃣ MM-algorithm

📕 지난시간에 배운 내용

• MM-algorithm은 lower bound를 사용하여 object function의 monotonic improvement를 보장한다.
• MM-algorithm에서 lower bound를 surrogate objective function으로 사용한다.
• MM-algorithm에서 surrogate objective function을 maximize하는 파라미터를 찾는다.
• 해당 파라미터를 new policy로 업데이트한다.
• 이 과정을 반복하여 Object function의 optimal policy에 도달한다.

---

4️⃣ Constraint object

📕 지난시간에 배운 내용

• KL penalized objective 항을 제약조건 식으로 바꾸었다.
• Constraint 항을 trust region이라고 한다.
• Trust region 항에 Monte Carlo simulation을 적용하기 위해 max값을 expectation으로 바꾸었다.

---

5️⃣ Monte Carlo simulation

📕 지난시간에 배운 내용

$\max_\theta \sum_s \rho_{\theta_\text{old}}(s) \sum_a \pi_\theta(a|s) A_{\theta_\text{old}}(s, a) \quad \text{subject to} \quad \mathbb{E}_{s \sim \rho_{\theta_\text{old}}}\left[D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot | s) || \pi_\theta(\cdot | s))\right] \le \delta$

• 최종적으로 위 식이 도출된다.
• Expectation을 old policy로 sampling하여 구할 수 있다.
• Expectation 대신 sample averages를 사용한다.
• Q-value값은 Q-Network를 설계하여 구한다.

---

6️⃣ Practical algorithm

📕 지난시간에 배운 내용

$\max_\theta \sum_s \rho_{\theta_\text{old}}(s) \sum_a \pi_\theta(a|s) A_{\theta_\text{old}}(s, a) \quad \text{subject to} \quad \mathbb{E}_{s \sim \rho_{\theta_\text{old}}}\left[D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot | s) || \pi_\theta(\cdot | s))\right] \le \delta$

1. Sample data를 수집하고 Q-Network를 이용하여 Q-value값을 구한다.
2. Sample data를 통해 expectation 값을 구한다.
3. Natural Policy Gradient를 이용하여 파라미터를 업데이트한다.

---

7️⃣ Natural Policy Gradient

🔷 Tayor series를 통한 approximation

$\max_\theta L_{\theta_\text{old}}(\theta) \quad \text{subject to} \quad \bar{D}_{\text{KL}}(\theta_\text{old} || \theta) = \mathbb{E}_{s \sim \rho_{\theta_\text{old}}}\left[D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot | s) || \pi_\theta(\cdot | s))\right] \le \delta$

• NPG는 Objective function과 Constraint 식을 모두 Taylor series를 통해 근사한다.

$\max_\theta \nabla_\theta L_{\theta_\text{old}}(\theta)|_{\theta=\theta_\text{old}} (\theta - \theta_\text{old}) \quad \text{subject to} \quad \frac{1}{2}(\theta - \theta_\text{old})^T H (\theta - \theta_\text{old}) \le \delta$

• Objective function은 1차식만 근사한다.
• 1차식에는 1번 미분하여 사용된 gradient가 존재한다.
• Constraint 식은 2차식만 근사한다.
• 2차식에는 2번 미분하여 사용된 Hessian이 존재한다.
• Hessian은 2번 미분된 행렬이기 때문에 더 많은 연산량을 필요로 한다.
• Step size는 Constraint 식을 만족하는 범위 내에서 결정해야 한다.

$H = \nabla_\theta^2 \bar{D}_{\text{KL}}(\theta_\text{old} || \theta) = \left( \frac{\partial^2 \bar{D}_{\text{KL}}(\theta_\text{old} || \theta)}{\partial \theta_i \partial \theta_j}|_{\theta=\theta_\text{old}} \right)$

• 현재 사용된 Hessian $H$를 Fisher Information Matrix라고 한다.

$H \approx \left( \frac{1}{N} \sum_{n=1}^N \frac{\partial^2}{\partial\theta_i \partial\theta_j} D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot | s_n) || \pi_\theta(\cdot | s_n)) \right)|_{\theta=\theta_\text{old}}$

• 실제 모델에 적용할 때는 Minibatch sample data를 사용하여 그 값을 구한다.
• 따라서 각 sample에 대한 식을 구한 후 N개에 대한 average를 구해야 한다.

🔻 Objective function은 1차식까지 근사하는 이유

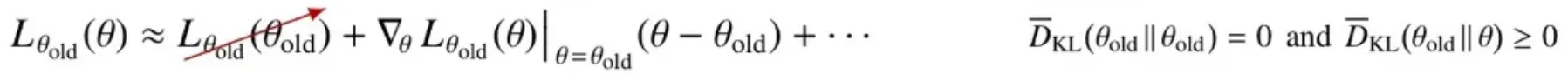
• 첫 번째 항, 즉 상수항은 $\theta_{old}$에 대한 식이라 maximize하는 $\theta$값에 영향을 주지 않는다.
• 2차식부터는 너무 작은 값이라 무시해도 된다.

🔻 Constraint 식은 2차식까지 근사하는 이유

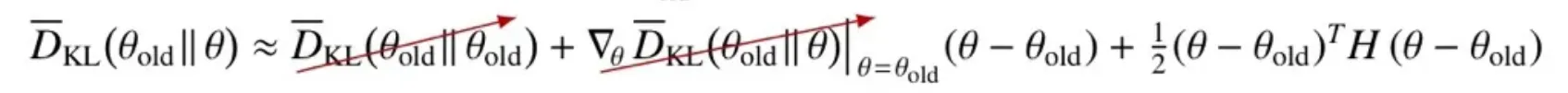
• 첫 번째 항, 즉 상수항은 같은 $\theta_{old}$에 대한 KL-발산 식이라 0이 된다.
• 두 번째 항은 KL-발산 식이 old policy에서 기울기가 0이 되기 때문에 사라진다.

🔷 Natural gradient

$H^{-1}\nabla_\theta L_{\theta_\text{old}}(\theta)|_{\theta=\theta_\text{old}}$

• 기존의 gradient에 Hessian의 inverse를 곱한다.
• 해당 식이 Natural gradient이다.
• Natural gradient를 통해 더 효율적으로 Object function의 Maximun값을 구할 수 있다.

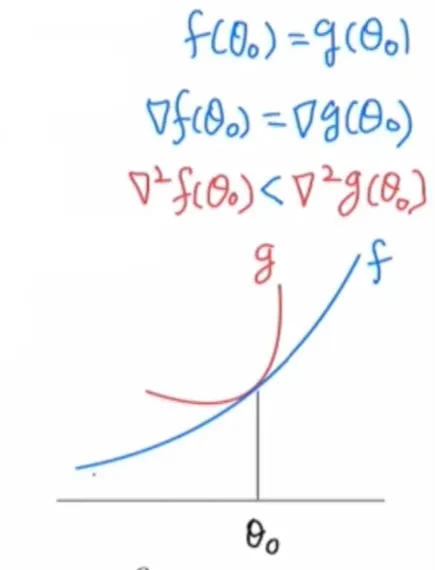
• Hessian $H$는 기울기의 휘어짐 정도를 의미한다.
• Natural Gradient를 사용하면 gradient의 휘어진 정도를 조정하여 목표지점에 빠르게 수렴할 수 있도록 한다.

🔻 파라미터 업데이트

• 기존의 파라미터에 Natural gradient와 step size $\beta$를 곱하여 구한다.

• 사용된 $H^{-1}$는 위 constraint 식을 만족해야 한다.
• Step size $\beta$는 위 부등식이 등호일 때 가장 큰 값을 가진다.

---

8️⃣ Conjugate gradient & Line search

🔷 Step size $\beta$

$\theta = \theta_\text{old} + \beta H^{-1}g \quad \text{satisfies} \quad \delta = \frac{1}{2}(\beta H^{-1}g)^T H (\beta H^{-1}g)$

• 가장 큰 step size $\beta$는 위 식을 만족할 때 성립한다.

🔷 파라미터 업데이트 식

$\theta = \theta_\text{old} + \sqrt{\frac{2\delta}{g^T H^{-1}g}} H^{-1}g \quad \text{where } g = \nabla_\theta L_{\theta_\text{old}}(\theta)|_{\theta=\theta_\text{old}}$

• KL-발산 Constraint 식을 만족하는 것은 Trust region을 만족하는 것이다.
• 위 Step size 내에서 Natural gradient를 통해 업데이트 하는 것은 Trust region 내에서 업데이트를 진행하는 것이다.
• 이를 Natural Policy Gradient라고 한다.
• 여기서 사용된 $g$가 기존에 사용되었던 policy gradient를 의미한다.

🔻 Hessian 구하기

• Hessian값은 많은 양의 연산량을 요구한다.
• 또한 Inverse를 구하는 것은 더욱 어렵다.

$\theta = \theta_\text{old} + \sqrt{\frac{2\delta}{g^T H^{-1}g}} H^{-1}g \quad \text{where } g = \nabla_\theta L_{\theta_\text{old}}(\theta)|_{\theta=\theta_\text{old}}$

• 따라서 우리는 $H^{-1}$ 대신 $H^{-1}g$ 를 구한다.
• $x=H^{-1}g$ 일 때, 이는 $Hx = g$의 해를 구하는 것이다.

$\min_x f(x) = \frac{1}{2} x^T H x - gx \quad \text{since } f'(x) = Hx - g = 0$

• 이는 위 식의 해를 구하는 것으로 바꿀 수 있다.

🔷 Conjugate gradient

$\min_x f(x) = \frac{1}{2} x^T H x - gx \quad \text{since } f'(x) = Hx - g = 0$

• 이때 $H$는 positive definite matrix이다.
• 이 경우 기존의 gradient descent 대신 Conjugate gradient를 사용할 수 있다.
• Conjugate gradient를 사용하면 더 빠르게 수렴할 수 있다.

🔷 Line search

• 우리는 Natural gradient descent를 통해 new policy를 구할 수 있다.

• 하지만 Objective function에 많은 approximation을 사용했기 때문에 성능이 monotonic하게 improve된다는 보장이 없다.

• 또한 KL-발산 제약조건 식 역시 많은 approximation을 거쳐서 monotonic하게 improve된다는 보장이 없다.

• 우리는 approximation을 하였지만 최대한 허용 가능한 step size $\beta$를 구하였다.

• Line search는 우리가 구한 step size $\beta$가 정말 안전한 것인지 확인하는 방법이다.

• $\beta$값을 objective function과 Constraint 식에 대입하여 두 식을 만족하는지 확인한다.

• 제약조건식이 $\delta$보다 큰 값이 나오거나, 성능이 improve 되지 않는다면 $\beta$값을 줄여준다.

• $\beta$값은 $\alpha$를 곱해주는 방법으로 줄여준다.

• $\beta$값이 조건을 만족할 때까지 $\alpha$를 곱해준다.

---

9️⃣ TRPO의 pseudo code

🔷 Pseudo code

🔻 파라미터 초기화

• Policy parameter를 초기화한다.

🔻 Iteration

• 1번의 Iteration마다 policy updata가 한번 수행된다.

• Old policy에서 sample data를 수집한다.

• Sample data를 통해 Advantage value나 Q-value를 구한다.

• Advantafe estimate를 이용하여 gradient를 구한다.

• $Hx = g$ 식에 Conjugate gradient를 적용하여 $H^{-1}g$를 구한다.

• $H^{-1}g$를 통해 Natural gradient를 구한다.

• $\beta$값에 Line search를 적용하여 제약조건 식을 만족하며 성능이 향상되는 $\beta$값을 구한다.

• 해당 $\beta$값을 통해 파라미터 업데이트를 진행한다.

🔷 TRPO의 단점

• TRPO는 second order optimizer를 사용한다.
• 그 결과 Adam과 같은 first order optimizer에 비해 sample efficient가 떨어진다.
• Hessian $H^{-1}$를 $H^{-1}g$를 통해 구하지만 이 역시 많은 연산량을 필요로 한다.
• 또한 Hessian $H$ 자체를 구하는데도 많은 연산량을 필요로 한다.
• 따라서 Deep CNN이나 RNN처럼 파라미터가 많은 경우 TRPO을 practical하게 적용할 수 없다.

---

🔟 정리

🔷 29강에서 배운 내용은 아래와 같다.

1. Natural gradient는 Hessian을 적용한 gradient이다.
2. Hessian을 통해 기울기의 기울어진 정도를 조정하여 수렴 속도를 높인다.
3. Conjugate gradient를 통해 Hessian값을 구한다.
4. Linesearch를 통해 제약조건을 만족하는 step size $\beta$를 구한다.
5. TRPO는 성능이 향상된다는 이점이 있지만, 그와 동시에 연산량이 많다는 한계가 존재한다.