👨‍🏫학습목표

오늘은 C51 모델과 C51의 핵심아이디어에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=xsLqA8a1Be4&t=1689s

C51 논문: https://arxiv.org/pdf/1707.06887

1️⃣ C51

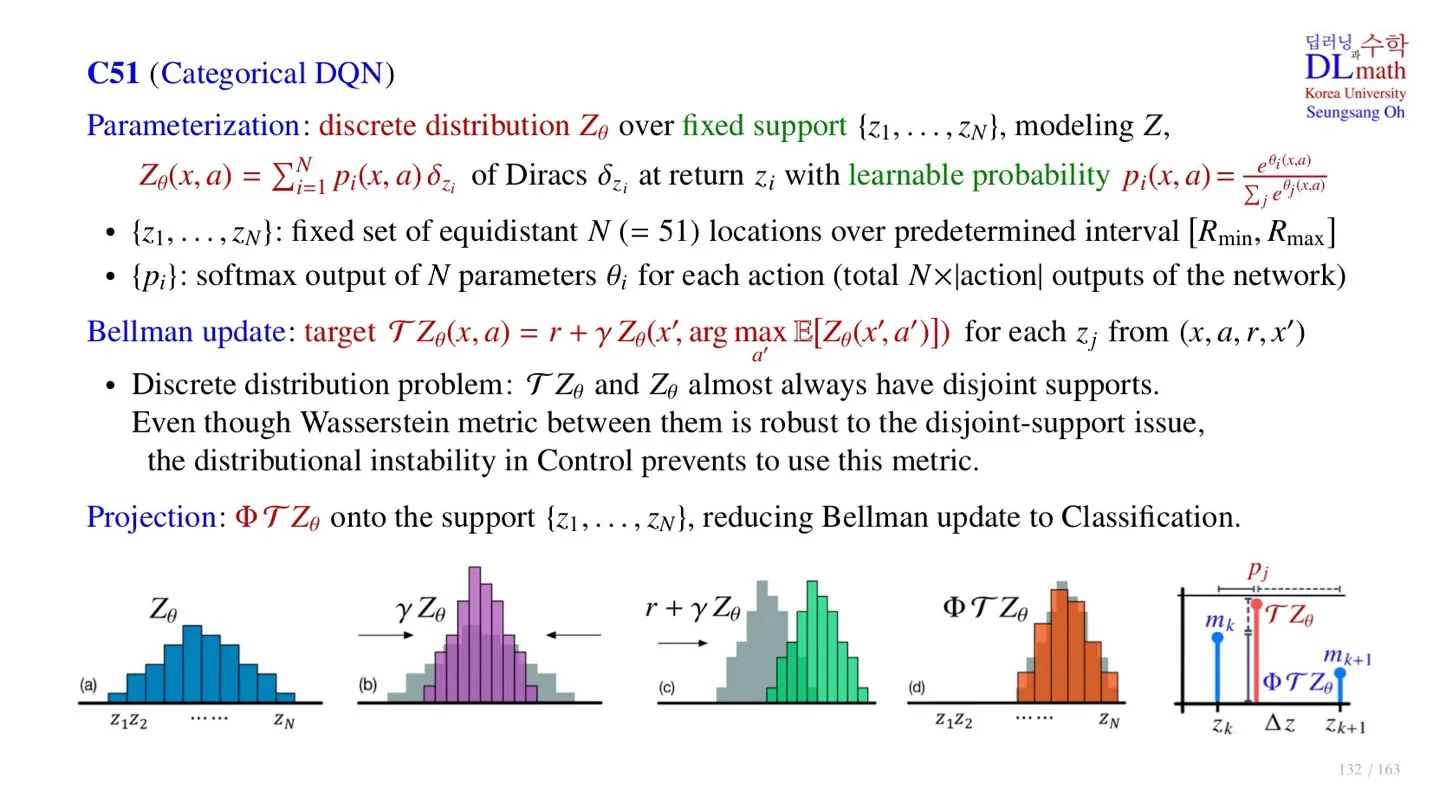
🔷 Categorical DQN

• Distribution을 출력한다.
• Parameterization, Bellman update Projection으로 구성되어 있다.

🔷Parameterization

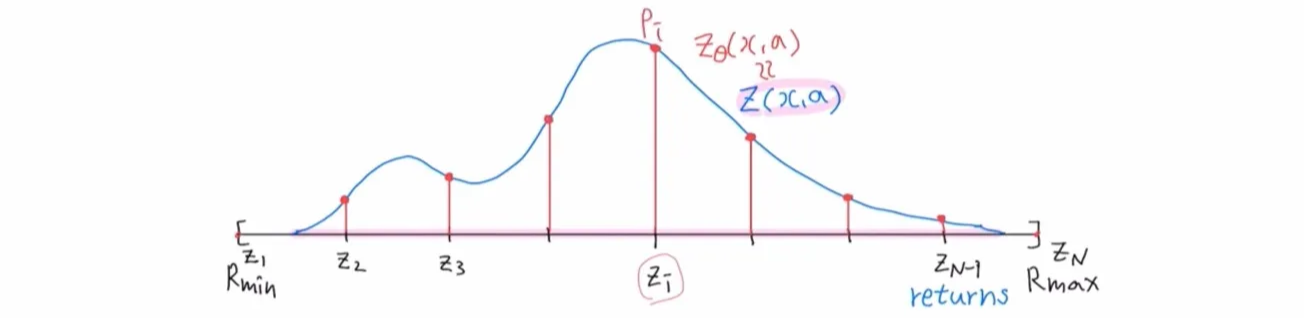
• 실제 Distribution $Z$를 discrete distribution $Z_{\theta}$로 만드는 과정이다.

• $N$개의 fixed support $\{z_1, \dots,z_N\}$을 사용한다.

• 즉 $z_i$에서만 확률값을 가진다고 이해하면 된다.

• fixed support $\{z_1, \dots,z_N\}$의 범위는 $[ R_{min}, R_{max}]$로 제한한다.

$Z_\theta(x, a) = \sum_{i=1}^N p_i(x, a) \delta_{z_i} \ , \quad p_i(x, a) = \frac{e^{\theta_i(x, a)}}{\sum_j e^{\theta_j(x, a)}}$

• Dirac $\delta_{z_i}$ at return $z_i$
• $p_i(x, a)$ 는 학습 가능하다.
• $p_i(x, a)$는 softmax 형태로 학습을 수행한다.
• C51 모델은 support에서의 확률값 $p_i(x, a)$를 출력한다.

🔻 Dirac function

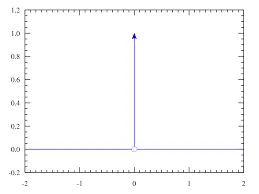
출처: https://www.thoughtco.com/dirac-delta-function-3862240

$\delta(x) = \begin{cases} \infty, & \text{if } x = 0 \\ 0, & \text{if } x \neq 0 \end{cases}$

$\int_{-\infty}^{\infty} \delta(x) \, dx = 1$

• 오직 한점에서만 0이 아니며, 그 점의 값은 무한하지만 적분 넓이는 1인 함수이다.

🔻 C51의 출력

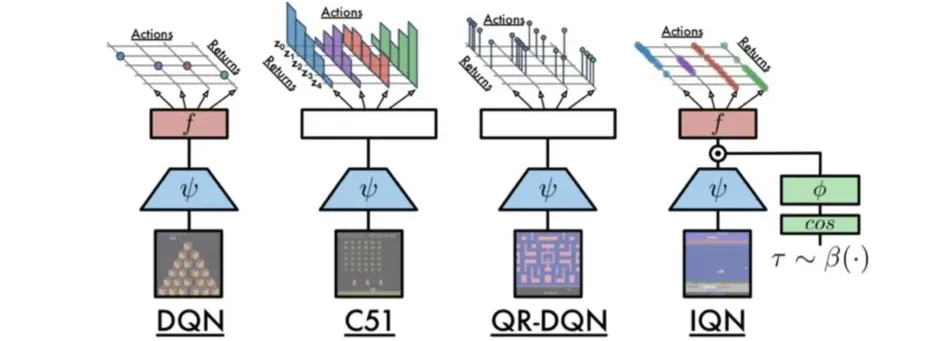
• C51은 각 action $a_i$에 대한 distribution을 출력한다.
• 이때 continuous한 distribution이 아닌 discrete한 distribution을 출력한다.
• Discrete distribution을 나타내기 위해 하나의 aciton $a_i$에 대해 총 $N$개의 $p_i(x, a)$를 출력한다.

$p_i(x, a) = \frac{e^{\theta_i(x, a)}}{\sum_j e^{\theta_j(x, a)}}$

• 실제 네트워크의 출력은 $\theta_i$이고, 우리는 softmax를 통해 정확한 확률값을 구한다.
• 총 $N \times |action|$ 개의 출력을 가진다.

🔷 Bellman update

• DQN은 Replay Buffer에서 minibatch 크기의 sample $(x, a, r, x')$ 을 가진다.
  
  

$\mathcal{T}Z_\theta(x, a) = r + \gamma Z_\theta(x', \arg \max_{a'} \mathbb{E}[Z_\theta(x', a')])$

• Target $\mathcal{T}Z_\theta(x, a)$와 behavior $Z_\theta(x, a)$ 의 차이가 줄어들도록 학습한다.
• 하지만 이때 두 분포의 support가 다를 수 있다는 문제가 발생한다.

🔻 Distribution의 변화

• Return $Z_\theta(x, a)$에 discount factor $\gamma$를 곱하면 distribution이 수축한다.
• 이때 확률 $p_i(x, a)$는 변하지 않는다.
• 또한 Imediate reward $r$를 더하면 distribution이 평행이동한다.
• 따라서 Target $\mathcal{T}Z_\theta(x, a)$와 behavior $Z_\theta(x, a)$ 의 support가 다를 수 있다.

🔷 Projection

• Projection 연산을 통해 support가 동일한 distribution을 만든다.
• Support가 동일해졌다면 KL-발산을 통해 차이를 계산한다.

---

2️⃣ C51의 pseudo code

📕 지난 시간에 배운 내용

• 두 분포의 차이를 계산하기 위해 Wasserstein metric을 사용하였다.
• Wasserstein metric은 두 분포가 멀리 떨어져 있어도 학습이 가능하다는 장점이 있다.
• 하지만 SGD를 사용하여 학습할 수 없다는 한계가 존재한다.
• 물론 다음 시간에 배울 QR-DQN은 Wasserstein metric을 사용하여 학습할 수 있도록 극복하였다.
• C51은 Wasserstein metric 대신 KL-발산을 사용하여 학습을 수행한다.

🔷 C51의 Loss function

• C51은 KL-발산을 사용하여 학습을 수행한다.
• 이때 Support가 달라질 수 있다는 문제는 projection을 통해 극복하였다.

$D_{\text{KL}}(\Phi \hat{\mathcal{T}} Z_\theta(x, a) || Z_\theta(x, a))$

• Target $\mathcal{T}Z_{\hat\theta}(x, a)$와 behavior $Z_\theta(x, a)$의 KL-발산을 구한다.

• 이때 Behavior Network는 $\theta$를 Target Network는 $\hat\theta$을 사용하는 것을 확인할 수 있다.

• 실제로 optimize과정은 $\theta$에 대해서만 이루어지며 $\hat\theta$은 상수로 처리한다.

$D_{\text{KL}}(P || Q) = \int_x P(x) \log \frac{P(x)}{Q(x)} dx$

$= \sum_i P_i(x) \log P_i(x) - \sum_i P_i(x) \log Q_i(x)$

• 실제 KL-발산 연산이 이루어질 때는 $x$는 return $z$를 의미한다.

• Return은 discrete하게 처리하기 때문에 $\sum$으로 표현할 수 있다.

• 또한 마지막 행의 첫째 항은 $\hat\theta$에 대한 식이기 때문에 상수 취급하여 실제 loss는 2번째 항이다.

• $- \sum_i P_i(x) \log Q_i(x)$ 형태의 cross-entropy loss이다.

🔷 DQN과 C51의 차이점

1. DQN은 Q-value function을 출력하지만, C51은 action-value distribution을 출력한다.

2. C51에서는 practical하게 적용하기 위해 Distribution을 discrete하게 변환하였다.

3. DQN은 학습을 위해 Target Network와 Behavior Network의 MSE를 사용하지만, C51은 KL-발산의 cross-entropy loss를 사용한다.

🔻 DQN의 pseudo code

• Replay Buffer에서 sample data를 추출한 후 MSE를 계산하는 것을 확인할 수 있다.

DQN의 pseudo code에 대한 추가적인 내용은 아래 글에서 확인 가능하다.

📃자료: https://velog.io/@tina1975/Deep-Reinforcement-Learning-18강-DQN-2

🔻 C51의 pseudo code

• Sample data를 이용하여 return $Z_{\theta}(x_t, a_t)$를 구한다.

• Q-value를 maximize하는 action을 next action으로 정한다.

• Sample data를 활용하여 Target return $\mathcal{T}Z_{\hat\theta}(x, a)$를 구한다.

• $m_k :$ $\mathcal{T}Z_{\hat\theta}(x, a)$를 의미한다.

• $- \sum_i m_i \log p_i(x_t, a_t):$ Cross-entropy loss를 구한 것을 확인할 수 있다.

---

3️⃣ 정리

🔷 32강에서 배운 내용은 아래와 같다.

1. C51은 Discrete Distribution을 학습한다.
2. Parameterization 과정을 통해 discrete한 return을 생성한다.
3. Target value를 구하는 과정에서 support가 변하는 문제가 발생한다.
4. Projection 과정을 통해 support가 변하는 문제를 해결한다.
5. 실제 loss function은 cross-entropy 형태를 띄고 있다.