👨‍🏫학습목표

오늘은 optimal policy를 계산하기 위한 기본 개념 Expected Reward, Return에 대해 배워볼 예정이다.

👨‍🎓강의영상: https://www.youtube.com/watch?v=Mvzu5CwcUpw&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=4

1️⃣ Reward Hypothesis

🔷 Reward $R_t$ 란?

• 시간 $t$에서 agent의 행동에 대한 피드백으로 스칼라값이다.
• Agent는 이러한 Reward값들의 합을 최대화하는 방향으로 학습한다.
• 기존의 Loss 함수 방식이 오차를 줄여나가는 방식이라면, 강화학습은 선호도를 극대화하는 방향으로 학습하는 것이다.
  
  

🔷 Reward Hypothesis

Policy가 나타날 수 있는 모든 episode의 reward를 구한 후, 이 reward의 기대값을 최대화하는 Policy를 구하면 된다.

🔷 학습하는 내용에 따라 Reward가 제공되는 횟수는 다르다.

• 바둑: 모든 게임이 끝난 후 마지막에 reward를 한번 제공
• 핑퐁: 게임이 진행되는 중간중간 득점이 이루어질 때마다 reward 제공

2️⃣ Expected Reward

🔷 State transition probability

🔻 state transition probability에서 마지막 항이 성립하는 이유.

• 우변이 $r$에 대한 시그마로 표현된 이유는, 하나의 action에 대해 받을 수 있는 모든 reward를 합했기 때문이다.
• 여기서 주의할 점은 모든 reward가 동시에 발생하지는 않는다. 수식의 등호를 만족하기 위한 전확률 공식이라고 이해하면 된다.

🔻 왜 이런 정의를 할까?

지하철을 타러 가는 상황으로 비유하면, 집에서$(S_t)$ 지하철로 이동하여 $(A_t)$, 지하철에 탑승한다$(S_{t+1})$는 state transition이 있을 때, 지하철의 쾌적도(환경)에 따라 reward가 달라질 수 있다. 즉 동일한 state transion에 대해서도 다른 reward가 제공될 수 있기 때문에 이러한 경우를 모두 고려하여 확률을 세분화할 필요가 있다.

🔷 Expected reward for state-action pair

• $R_s^a:$ 가능한 모든 next state를 고려하여 계산된 보상의 기대값.
• 유의점: $s'$과 $r$은 서로 의존적이기 때문에 $\sum$을 개별적으로 계산하기는 힘들다.

🔷 Expected reward for state-action-next_state triple

🔻 마지막 항은 조건부확률의 정의에 따라 아래와 같이 정리할 수 있다.

3️⃣ Return: 하나의 Episode에 대한 Reward

• $G_t:$ 현재 시간 $t$에서부터 앞으로 받게 될 reward에 감가율을 적용하여 구한 총 할인된 reward. 하나의 episode에 대한 할인된 reward라고 생각하면 된다.
• $R_{t+k}:$ 모델이 해당 시점에서 실제로 받은 reward.
• $\gamma:$ Discount factor, 모델의 action 결과, 즉 미래의 state가 stochastic하기 때문에 미래에 받게 될 reward에는 불확실성이 내포되어 있다. 따라서 불확실한 정보일수록 적게 반영하기 위해서 감가율 $\gamma$를 적용하여 불확실성이 내포된 reward의 가치를 줄인다. 그 외에도 미래에 대한 reward보다 현재의 reward에 더 집중할 수 있도록 한다.

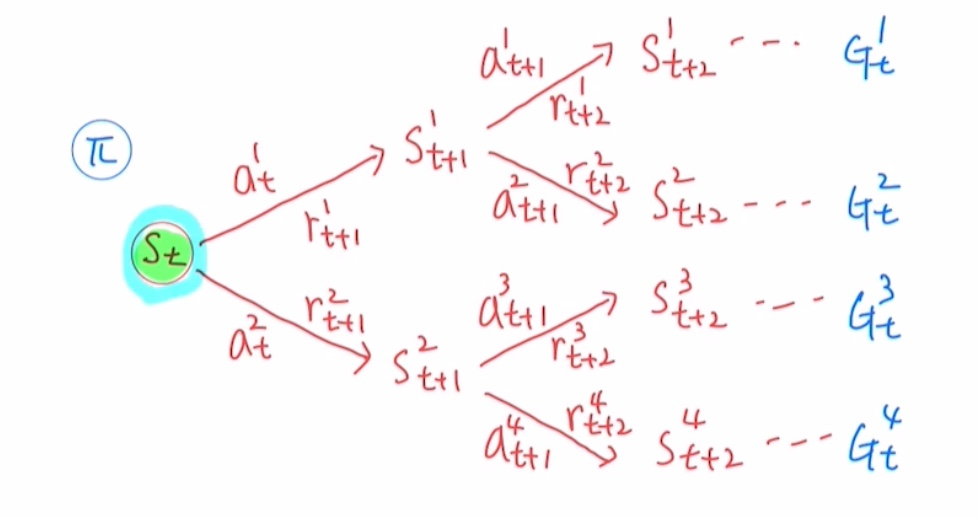
4️⃣ Policy에 따라 발생하는 여러 Episode

• 강화학습의 목적은 최적의 policy를 찾는 것이다.
• $\pi: S \rightarrow A,$ 주어진 state에서 어떤 action을 취할지에 대한 확률 분포이다.

🔷 여러 종류의 episode

🔻 1. 동일한 (상태, 행동) 쌍에서 다른 보상을 받은 경우

• 예: 집 $(S_t)$ 에서 지하철 이동 $(A_t)$ 후 '지하철 내부' $(S_{t+1})$에 도착했지만, 한 에피소드에서는 '한산해서 +20점'을, 다른 에피소드에서는 '혼잡해서 -15점'을 받은 경우.
• 이들은 보상이 다르므로 별개의 에피소드(또는 에피소드 내의 다른 확률적 결과)로 간주한다.

🔻 2. 동일한 (상태, 행동) 쌍에서 다른 다음 상태로 이동한 경우

• 예: 집 $(S_t)$에서 '차량 호출' $(A_t)$ 행동을 했을 때, 한 에피소드에서는 '택시 탑승' $(S_{t+1})$에 성공했지만, 다른 에피소드에서는 '호출 실패 후 버스 정류장' $(S'_{t+1})$으로 이동한 경우.
• 이들은 다음 상태가 다르므로 별개의 에피소드로 간주한다.

🔻 3. 다른 행동을 취한 경우

• 예: 집 $(S_t)$에서 한 에피소드에서는 '지하철 이동' $(A_t)$을 선택하고, 다른 에피소드에서는 '버스 이동'$(A'_t)$을 선택한 경우
• 행동 자체가 다르므로 당연히 별개의 에피소드로 간주한다.

이때 $G_t$를 시점 $t$부터 계산하는 이유는, Markov Decision Process가 과거의 state에 의존하지 않고, 현재의 state에 의존하기 때문이다.

🔷 State transition probability를 알고 있는 경우와 모르는 경우

🔻 1. Under known MDP

• transition probability를 모두 알고 있기 때문에 $E(G_t)$ 를 모두 계산할 수 있다.
• optimal policy $\pi_*(s)$가 명확하게 존재한다.

🔻 2. Under unknown MDP

• $\epsilon$-greedy policy
• 가지고 있는 sample data를 통해 optimal policy를 결정한다.
• 하지만 수집된 sample data(경험)는 환경의 모든 가능한 상태-행동 transitiond을 포함하지 못할 수 있으며, 이로 인해 아직 탐험되지 않은 경로에 더 나은 최적 정책이 존재할 가능성이 있다는 한계가 존재한다.
• 따라서 $\epsilon$ 만큼의 확률로 다른 action을 취할 수 있도록 설계하여, 모델의 성능이 개선될 수 있도록 설계한다.

5️⃣ 기호 정리

• arg: argument로 인자 혹은 입력으로 이해하면 된다.

• $v_\pi(s):$ 주어진 policy $\pi$에 대하여, 현재 state $s$에서 가능한 episode의 $G_t$의 기대값 즉 $E(G_t)$에 대한 함수, 현재의 state가 좋은 state인지 아닌지를 판단하는 기준이 된다.

• $v_*(s):$ optimal policy $\pi_*$에서의 state-value function

• $q_\pi(s, a):$주어진 policy $\pi$에 대하여, 현재 state $s$에서 특정 action $a$를 취했을 때, 발생할 수 있는 episode의 $G_t$의 기대값, 즉 $E(G_t)$에 대한 함수, 현재 state에서 해당 action이 좋은 선택인지 아닌지를 판단하는 기준이 된다.

• $q_*(s, a):$ optimal policy $\pi_*$에서의 action-value function

6️⃣ 정리

🔷 4강에서 배운 내용은 아래와 같다.

1. 강화학습의 기본 가정: Reward Hypothesis
2. Reward의 기대값에 대한 수학적 정의
3. 해당 state에서 미래에 받을 수 있는 Reward 시나리오, Return, $G_t$
4. 다양한 종류의 episode
5. 강화학습의 기본 구조: $\epsilon$-greedy policy