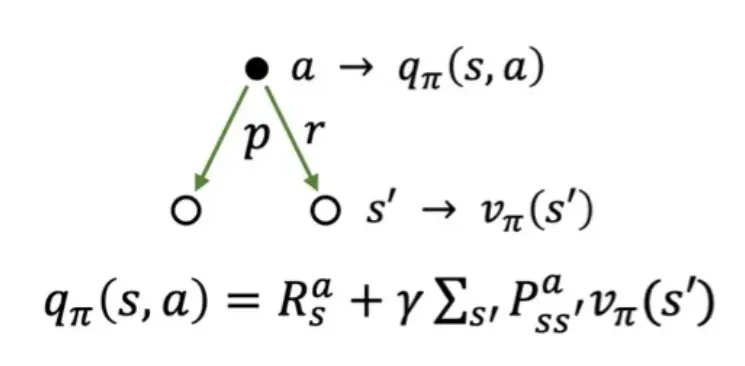👨🏫학습목표
오늘은 Bellman Equation과 이를 활용한 Sate-value function, Action-value function의 분해에 대해 배워볼 예정이다.
1️⃣ Value functions

🔷 State-Value function
- 현재의 state가 좋은 state인지 아닌지 평가해주는 역할을 한다.
- 입력된 state가 앞으로 얼마나 많은 보상을 얻을지 출력한다.
vπ(s)=Eπ[Gt∣St=s]
- 현재 state는 정해진 policy π에 따라 state transition을 한다.
- 이때 다양한 episode로 state transition을 할 수 있고, 각 episode가 발생할 확률과 받게 될 return이 존재한다.
- 이 둘을 가중합으로 계산하여 각 state가 받게 될 기대 return을 구할 수 있다.
vπ(s)=a∑π(a∣s)qπ(s,a)
- vπ(s): 현재 state에서의 총 reward의 기대값
- π(a∣s): 현재 state에서 각 action을 취할 확률
- qπ(s,a): 각 action을 취했을 때 발생하는 episode의 총 reward 기대값
🔷 Episode의 stochastic
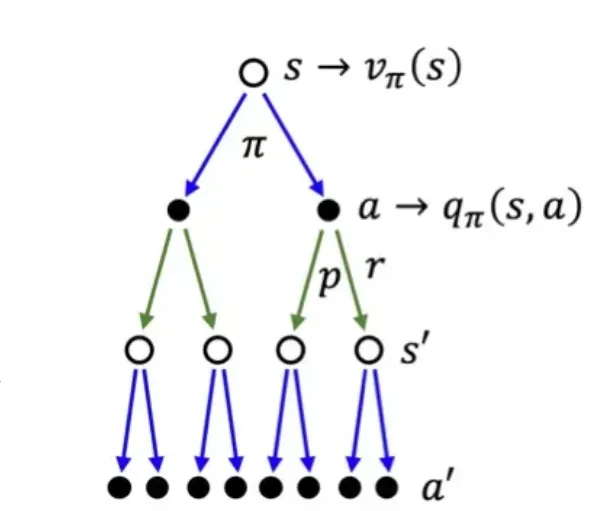
Episode : s0,a0,r1,s1…
- s0→a0: policy π에 따라 결정된다, π는 확률 분포이기 때문에 stochastic하다.
- (s0,a0)→s1: state transition probability p에 따라 결정, stochastic하다.
- 위 그림처럼 stochastic한 경우를 모두 표시한 것을 Backup diagram 이라 한다.
- 각각의 분기선이 하나의 episode이다.
🔷 Action-Value function
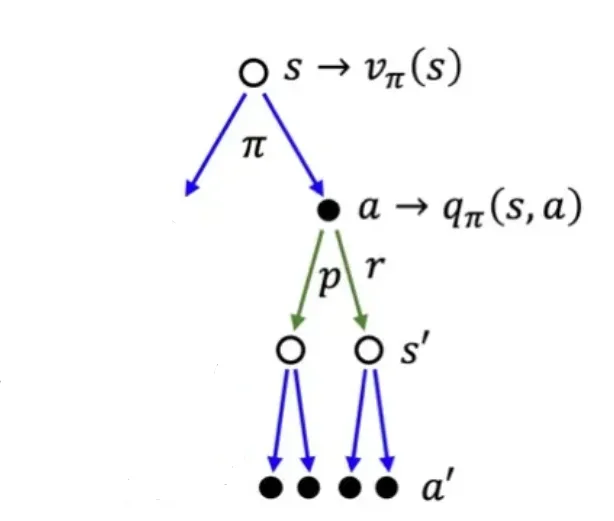
qπ(s,a)=Eπ[Gt∣St=s,At=a]
- 하나의 state에서 특정 aciton을 취한 후 얻게 될 미래 총 보상의 기대값이다.
- 현재 state에서 어떤 action을 취하는 것이 좋은지 평가해주는 역할을 하므로, Policy π를 결정하고 개선하는 데 유용하다.
- 다만 St와 At의 pair를 계산해야 하기 때문에 연산량이 증가한다.
- 강화학습은 Model-free이기 때문에 random sample을 통해서 기대값을 추정한다.
- Ramdom sample의 수가 많아질수록 추정치의 값은 실제 기대값에 더 가깝게 근사한다.
- 이 방법을 Monte Carlo라고 한다.
몬테카를로(Monte Carlo) 방법은 무작위 샘플링(random sampling)을 사용하여 기대값이나 확률을 추정하는 계산 알고리즘의 한 종류입니다.
🔷 Advantage function
Aπ(s,a)=qπ(s,a)−vπ(s)
- 수식의 의미: 특정 action에서의 총 reward의 기대값과 모든 action의 총 reward의 기대값의 차이
- Aπ(s,a)>0이면 해당 action이 평균보다는 좋은 선택이라는 의미이다.
2️⃣ 중요한 확률 이론

전확률 공식과 큰 수의 법칙에 대해 알아본다.
3️⃣ Bellman Expectation equation

🔷 State-Value function 재귀적 분해
vπ(s)=Eπ[Gt∣St=s]
=Eπ[Gt∣St=s,At=a]⋅P(At=a∣St=s)
- Law of total probability에 따라 각 행동의 기대 return과 해당 행동을 할 확률의 가중합으로 표현하였다.
=a∑π(a∣s)Eπ[Rt+1+γGt+1∣St=s,At=a]
- 각 행동의 기대 return을 바로 받게 될 reward과 이후 총 return의 기대값으로 분해한다.
- Action마다 바로 받게 될 reward가 다르기 때문에 위 식처럼 Law of total probability을 통해 action을 구분한 후 분해하는 것이 타당하다.
=a∑π(a∣s)Eπ[Rt+1+γGt+1∣St=s,At=a,St+1=s′,Rt+1=r]⋅ P(St+1=s′,Rt+1=r∣St=s,At=a)
- 해당 기대값을 다시 St+1,Rt+1로 Case분류합니다.
- 다음 Reward로 무엇을 받을지 정확하게 구분한다고 이해할 수 있습니다.
=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]
- Markov property에 따라 St,At,Rt+1은 Gt에 영향을 주기 않기 때문에 조건에서 제거한다.
=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]
- 정의에 따라 vπ(s′)를 작성한다.
=a∑π(a∣s)⎝⎜⎛s′,r∑p(s′,r∣s,a)r+γs′,r∑p(s′,r∣s,a)vπ(s′)⎠⎟⎞
- 분배법칙에 따라 구분 한다. 각 항을 살펴보면
s′,r∑p(s′,r∣s,a)r=Rsa
- 첫 번째 항은 상태 s와 a가 주어졌을 때 받을 수 있는 모든 Reward의 기대값 Rsa이다.
γs′,r∑p(s′,r∣s,a)vπ(s′)
- 두 번째 항은 감가율이 상수이므로 ∑ 밖으로 빼준다.
=a∑π(a∣s)[Rsa+γs′∑Pss′avπ(s′)]
=Eπ[Rt+1+γvπ(St+1)∣St=s]
🔻 최종결론
vπ(s)=Eπ[Gt∣St=s]=Eπ[Rt+1+γvπ(St+1)∣St=s]
🔻 참고식
s′∑Pss′avπ(s′)=E[vπ(St+1)∣St=s,At=a]
a∑π(a∣s)E[vπ(St+1)∣St=s,At=a]=Eπ[vπ(St+1)∣St=s]
🔷 어떻게 활용되는가??
모르겠음.
🔷 Action-Value function 재귀적 분해
qπ(s,a)=Eπ[Gt∣St=s,At=a]
=s′,r∑p(s′,r∣s,a)[r+γa′∑π(a′∣s′)qπ(s′,a′)]
=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
4️⃣ Bellman Expectation Equation의 Backup Diagram
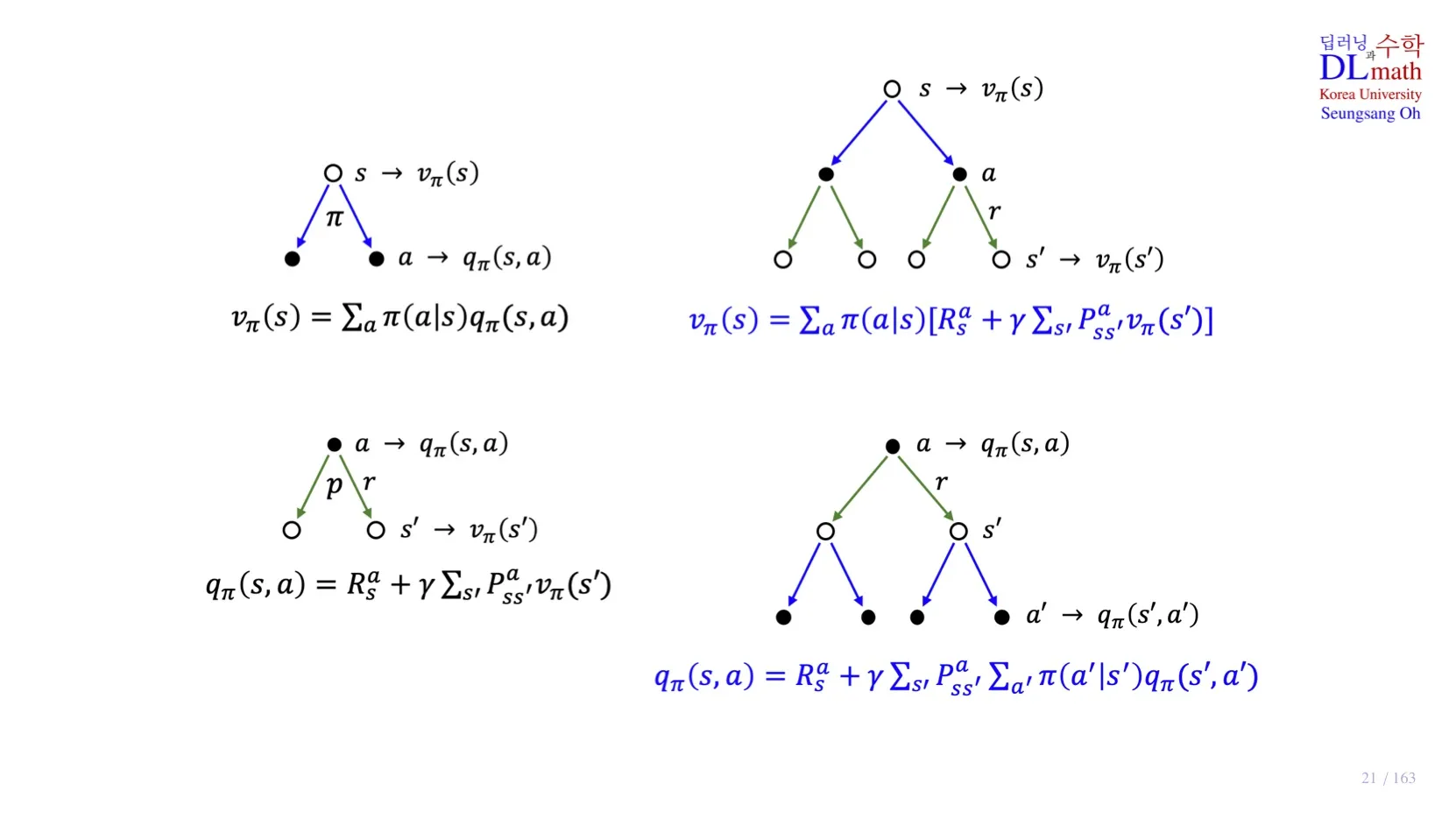
🔷 State-value function의 이해
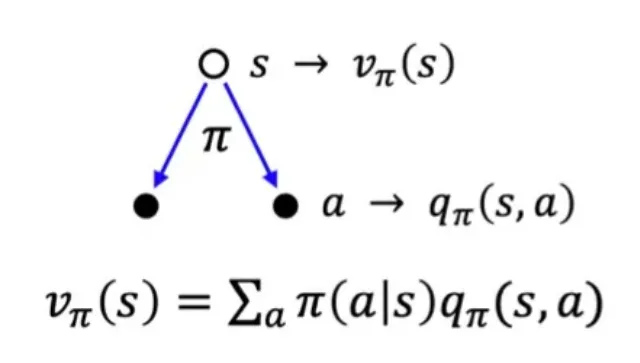
vπ(s)=a∑π(a∣s)qπ(s,a)
수식의 의미: vπ(s)은 각 action이 발생할 확률 π(a∣s) 와 해당 action으로 도달한 state가 받게될 return qπ(s,a)으로 구성된다.
🔷 Action-value function의 이해
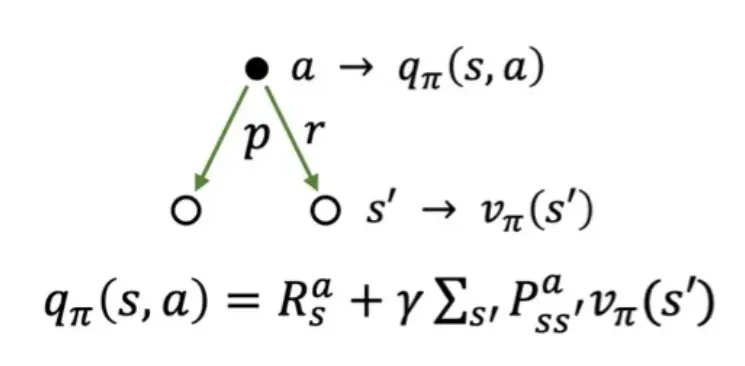
qπ(s,a)=Rsa+γs′∑Pss′avπ(s′)
수식의 의미: qπ(s,a) 해당 action으로 도달할 모든 state s′이 발생할 확률 Pss′a와 각 state에서 얻게 될 총 return의 기대값 vπ(s′)의 가중합, 그리고 각 state에 도달하는 과정에서 얻게 된 보상의 합 Rsa로 구성된다.
이렇게 분해한 두 식을 각각 서로 다른 식으로 채워넣으면 아래의 두 식이 유도된다.
vπ(s)=a∑π(a∣s)[Rsa+γs′∑Pss′avπ(s′)]
qπ(s,a)=Rsa+γs′∑Pss′aa′∑π(a′∣s′)qπ(s′,a′)
5️⃣ 정리
🔷 5강에서 배운 내용은 아래와 같다.
- Bellma Expectation Equation
- State-value function의 간단한 분해
- Action-value function의 간단한 분해
- State-value function의 재귀적 분해
- Action-value function의 재귀적 분해